Here is a question I asked myself yesterday: Suppose that X is an algebraic space which has degree 2 finite etale covering X_2 —> X and a degree 3 finite etale covering X_3 —> X such that both X_2 and X_3 are schemes. Is X a scheme?
I thought there might be a chance that the answer is yes, but just now in the common room, Philip, Anand, Davesh, and me proved that the answer is: no!
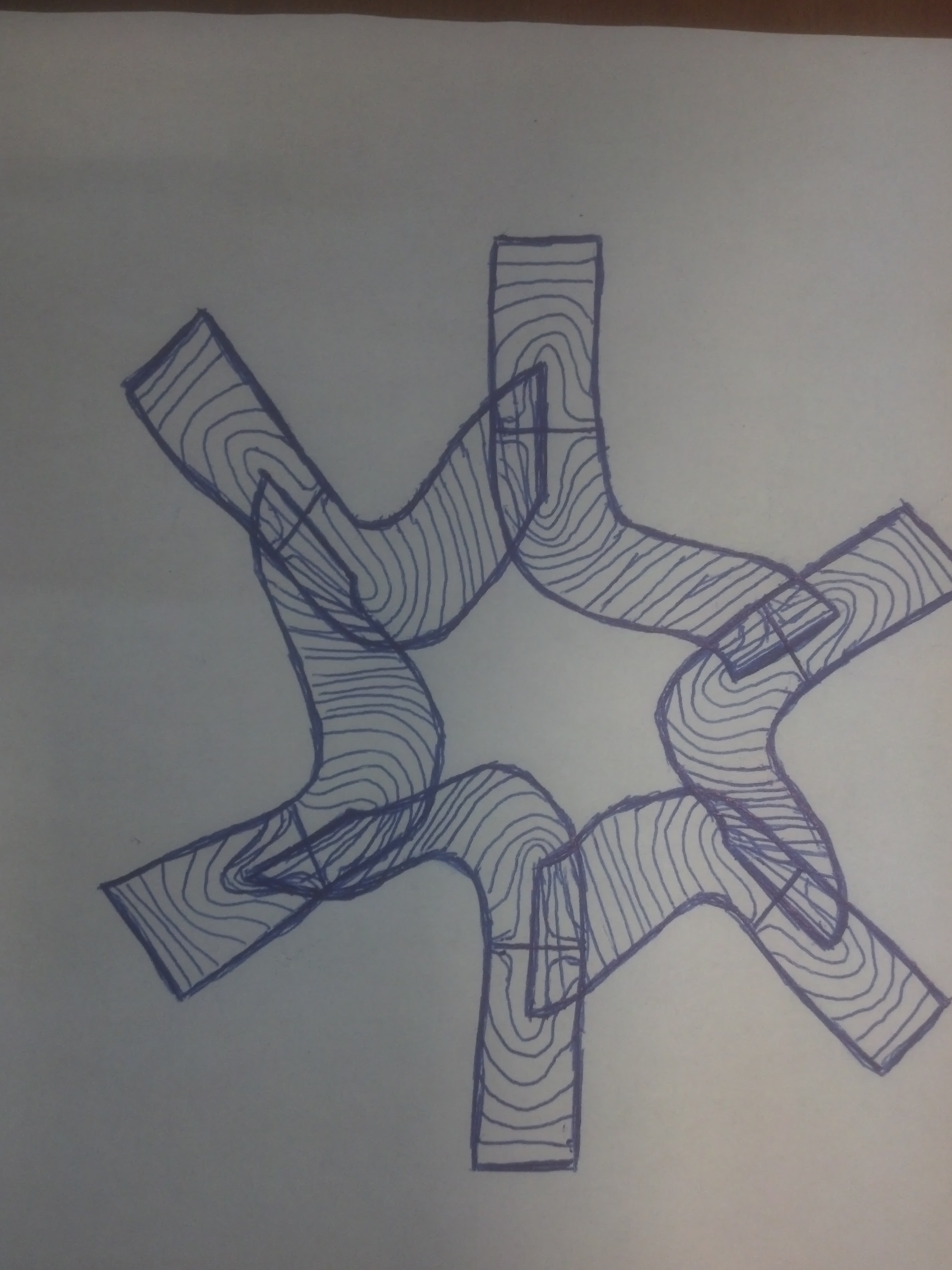
Namely, following Hironaka’s example, we made a smooth proper 3-fold X_6 with an action of a cyclic group G of order 6 such that X = X_6/G is not a scheme, but the two intermediate quotients X_2 and X_3 are schemes. Namely, start with a smooth projective 3-fold Y with an action of G and a 6-gon of smooth rational curves C_0, C_1, C_2, C_3, C_4, C_5 which are cyclically permuted by G. In other words, I mean that C_i ∩ C_{i + 1} is exactly one point P_i and the intersection is transversal. Then you do as in the Hironaka example: blow up all these curves but at P_i analytic locally blow up C_i first and C_{i + 1} second. The result is a proper scheme X_6 with an action of G. Over the P_i there are two curves E_i, E’_i such that E_0 + E_1 + … + E_5 is zero in the Chow group (see picture of Philip below). Hence orbit of a point on E_0 cannot be contained in an affine open of X_6, which proves that X_6/G is not a scheme. However, the morphism
X_6 – E_i ∪ E’_i —-> Y – P_i
is a usual blow up, hence the source is a quasi-projective variety and any finite collection of points is contained in an affine open. This quickly gives that X_3 and X_2 are schemes.
To finish, here is a picture X_6 (thanks Philip!):