The explanation for the lack of blogging here the past month is mostly that I haven’t seen any news worth blogging about. It took only a little bit of self-control to not do things like make snarky comments about recent conferences on string theory and quantum gravity.
Today I noticed a discussion on Twitter of the perennial question about what “spin” means in quantum theory, with some of the tweets included this highly appropriate meme: 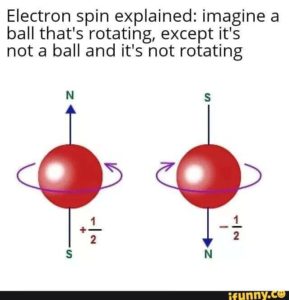
I thought it might be worth while to make a stab at explaining what “spin” really is. For a much more detailed version, I wrote a book. But this post is much shorter…
Picking a particular point and a particular direction (say the z-direction), the angular momentum $J_z$ is defined to be the “generator” of rotations about that point, around the z-axis. This means that when you do such a rotation by an angle $\theta$, for any observable (function of position and momentum) $F$
$$\frac{dF}{d\theta}|_{\theta=0}=\{F, J_z\}$$
where the bracket is the Poisson bracket. A short calculation shows
$$J_z=r_xp_y-r_yp_x$$
which is often given as the definition. $J_z$ is itself an observable, which you can say is the angular momentum about the z-axis of a point particle with x,y coordinates of its position and momentum given by $r_x,r_y,p_x,p_y$. In classical physics $J_z$ can take on any values.
In quantum mechanics, observables are operators acting on states, and $J_z$ becomes the operator $\widehat{J}_z$ which (with an additional factor of $-i$ to get unitary transformations) generates rotations on states. This means (using units such that $\hbar=1$)
$$\frac{d}{d\theta}\ket{\psi(\theta)}=-i\widehat J_z \ket{\psi(\theta)}$$
You can solve this differential equation and see that if you rotate a state by an angle $\theta$ about the $z$ axis, you get
$$\ket{\psi(\theta)}=e^{-i{\widehat J}_z\theta}\ket{\psi(0)}$$
States that are eigenvectors of ${\widehat J}_z$ are supposed to be the ones with a well-defined value of the classical observable $J_z$, given by the eigenvalue.
One finds experimentally that the observed values of $J_z$ are given by
$$\frac{n}{2}$$
Unlike the classical case, as expected this number is quantized (that’s why they call it quantum mechanics…), but the factor of $2$ is unexpected. Since a rotation by $2\pi$ should bring the state back to itself, one expects that
$$e^{-iJ_z2\pi}=1$$
so $J_z$ should be an integer. If one finds a state with $J_z=\frac{1}{2}$, rotating it by an angle $2\pi$ changes its sign. This is weird, but the sign of a state isn’t itself something you can measure.
Looking more closely at the operator $\widehat{J}_z$ for quantum systems, one finds that for some states it has exactly the same relation to position and momentum as in classical physics
$$\widehat{J}_z=\widehat{r}_x\widehat{p}_y-\widehat{r}_y\widehat{p}_x$$
When states are given by a wavefunction depending on spatial coordinates, one can show that this is just the expected action by infinitesimal rotation of the spatial coordinates. In this case rotation by $2\pi$ doesn’t change the state, and $J_z$ has integral (not half-integral) values.
For many quantum systems though, there is an extra term:
$$\widehat{J}_z=\widehat{r}_x\widehat{p}_y-\widehat{r}_y\widehat{p}_x+\widehat{S}_z$$
and it is this extra term $\widehat {S}_z$ that is the “spin” observable. When states are given by wavefunctions, what the equation above is telling you is that when you act on a state by a rotation, you get not just the expected induced action from the rotation on spatial coordinates, but also an extra term. A natural guess is that, as in the meme, a point particle is really a ball of some new stuff, with $\widehat {S}_z$ the effective extra term caused by the positions and momenta of the new stuff.
For an elementary particle such as an electron, experimentally one finds that $\widehat S_z$ has eigenvalues $\pm 1/2$, which explains why one sees half-integral quantization. As the meme says, there is no viable physical model of rotating stuff that would give this result. Something very different is going on.
So far I’ve stuck to talking about rotations about the z-axis, but one also should consider rotations about other axes. The problem is that more sophisticated mathematics is needed, since the generators of rotations around different axes don’t commute (doing the rotations in the opposite order gives a different result). The mathematics needed is that of the representation theory of the rotation group $SO(3)$ and its double-cover $SU(2)$. From this representation theory one learns that the only consistent possibilities are given by putting together copies of a “spin n/2” representation for $n=0,1,2,\cdots$. These are $n+1$-dimensional vector spaces, on which $\widehat{S}_z$ acts with eigenvalues
$$\frac{-n}{2}, \frac{-n +2}{2},\cdots,\frac{n-2}{2},\frac{n}{2}$$
The case $n=0$ is that of $\widehat{S}_z=0$, and the simplest non-trivial case is the $n=1$ case which gives $\widehat{S}_z$ for the electron.
So, the “spin 1/2” characteristic of the electron is something completely new, unrelated to anything in classical mechanics. If you describe the electron by a wavefunction, it will take values not in the complex numbers, but in pairs of complex numbers, with rotations acting on the pairs by the spin-1/2 representation (also known as the “spinor” representation). Besides the non-classical physical behavior, the geometry is also non-classical, with the spinor representation something that cannot be described by the usual formalism of vectors and tensors.
Another reason I haven’t been writing much on the blog this past month is that I’ve been working on writing up something about twistors. I’ll write about twistors in detail here when this is done, but one thing they do is give a picture of space-time geometry in which spinors are fundamental, not vectors. A fundamental idea of twistor theory is that a point in space-time is a complex two-plane inside complex four-space. In twistor theory the answer to the question of where the spinor degree of freedom at a point comes from is tautological: the two complex dimensional spinor degree of freedom at a point IS the point.
Bonus link for those who have gotten this far. A presentation by CERN director Fabiola Gianotti, which comes off a bit differently than news reports saying CERN is going ahead with FCC. On page 5
- Strategy gives a direction for future collider(s) at CERN (FCC). Prudent: feasibility study first.
- Intensified accelerator R&D to prepare alternatives if FCC feasibility study fails.
- No consensus in European community on which type of Higgs factory(linear or circular).
Page 9 lists three “first priorities” for the feasibility study:
- find funds for the tunnel
- [Be sure] no show-stoppers for ~100 km tunnel in Geneva region
- magnet technology [are the FCC-hh magnets feasible?]; how to minimise environmental impact



In order to help motivate my calculus students I often show how calculus can be used in sports; this actually often works. In particular, I often describe the motion of a curve ball in baseball. The configuration space of a baseball is R^3xSO(3) and its associated phase space is T*(R^3xSO(3)) ( the cotangent bundle of R^3xSO(3)). SO(3) is too complicated to describe to Freshman. So, instead, I use a simpler, though adequate, model of a baseball as a point particle with extra spin angular momentum. Now the phase space is T*(R^3)xS^2. The dynamical equations can now be set up and numerically solved and graphed on a graphing calculator. One can then watch the ball curve! The phase space (S^2,v) (use the canonical area 2-form v obtained by thinking of S^2 as the standard unit sphere in R^3) is not the cotangent bundle of any configuration space. For any s in R+, T*(R^3)x(S^2, s*v) provides a classical phase space of a point particle of spin s. Using Geometric Quantization (see: http://www.amazon.com/Geometric-Quantization-Oxford-Mathematical-Monographs/dp/0198502702/ref=pd_bbs_sr_1?ie=UTF8&s=books&qid=1219711387&sr=8-1
), one can quantize this phase space for s satisfying appropriate integrality conditions and obtain the usual quantum theory of spinning particles. For all s one can deformation quantize (see: http://www.amazon.com/Deformation-Quantization-Mathematicians-Mathematiques-Irma-Lecture/dp/311017247X/ref=sr_1_1?ie=UTF8&s=books&qid=1219711918&sr=1-1
) this phase space and get something that is probably also interesting!
Thus, Pauli was wrong! There are reasonable classical limits of spinning point particles.
Hi Peter,
listening to David Gross giving the final lecture on Strings 2020, it seems clear that he has surrendered to the fact that there are certain parameters that might not be calculable, and that they are just an “accident”. He might have come to the conclusion that his “never, never, never, never surrender” idea is wrong, and that things are tilting towards the anthropic principle/landscape idea. It might be worth of a comment… snarky or not.
And Witten’s answer to Vafa on the 40th and 41st minute on the latter’s talk re the completeness hypothesis might be willing of another comment too.
I think both comments seem to point in the same direction, that things are getting pretty murky when it comes to try and find a unique theory of the vacuum that describes our world.
”the “spin 1/2” characteristic of the electron is something completely new, unrelated to anything in classical mechanics”
Spin is not as quantum mechanical as you make it appear here. Indeed, the coadjoined orbits of the Poincare group provide phase spaces (Poisson manifolds) for classical particles with spin – for positive mass a 2-parameter family parameterized by mass $m$ and continuous spin $s$. Upon quantization, the coadjoined orbits turn into irreducible unitary representations, and the spin gets quantized in the same way as angular momentum gets quantized when quantizing its representation on the sphere. Nothing more than geometric quantization is involved.
David Edwards/Arnold Neumaier,
I’m a big fan of geometric quantization, but
1. It’s not the best way to understand the spinor degree of freedom.
2. The relation to classical physics is in the limit of large spin, with spin 1/2 the opposite limit, maximally non-classical.
DB,
To be blunt, I think the current situation with relating string theory to the real world is that most string theorists have simply given up. About the only active area in string theory that even tries is the Swampland business, which hardly anyone takes seriously. Given this situation, there’s no longer any science here worth trying to have a serious discussion about, all that remains is the sad sociological question of why people are still promoting string theory as our best hope for a unified theory. But, that’s also a tired subject, which I don’t want to encourage here unless someone actually has something new to say about this.
Dear Peter,
Thank you for the clear explanation of spin 1/2 behaviour.
Whilst you are considering the twistor geometric implications could you please put your mind to what additional extension is needed to give rise to the 3 neutrino types?
Could a point in space-time be more than a complex 2-plane?
How about a 3-sphere?
Dear professor:
My name is Manuel del Rio and I am an avid and enthusiastic follower of your blog and your work. Good to have you back, even if nothing of late tickled your fancy! As you mention your book: it is in my top 5 of books I really want to be able to read in the future (right now, it is hopelessly out of my range; I am a Humanities person and English teacher for adults here in Spain, and have just started an online math degree which will have to progress very slowly -work and son must take priority-).
Even though it will probably have to wait a decade to be read, I will be buying it in the next months. Are you planning a second edition any time soon (incorporating the errata you mention in your page?)? If that were the case, I would wait for the purchase until it is out.
Best greetings
Manuel
Perhaps the following historical question might be on topic for this post.
-i times the Pauli matrices gives a representation of Hamilton’s quaternions. After struggling for a long time to find a generalization of the complex numbers, Sir William Rowan Hamilton suddenly thought of quaternions during a walk in 1843, and he famously scratched his inspiration on a bridge near Dublin. I had assumed that what he scratched on the bridge was something like -i times the Pauli matrices, but in fact what he wrote was $i^2 = j^2 = k^2 = i j k = -1$.
It would be nice to think that Hamilton discovered something like the Pauli matrices 177 years ago. But on skimming through nineteenth century textbooks on quaternions, such as those available on gutenberg.org, no trace of a 2-dimensional representation of the quaternions, or any matrix representation of the quaternions, ever seems to show up.
Élie Cartan constructed the spinor representations of the orthogonal groups in his 1913 paper that constructed, in the sense of their weight spaces, all the irreducible linear representations of the simple compact Lie algebras, (Bulletin de la S. M. F., tome 41 (1913), p. 53-96). The results for the Lie algebras of type $B_l$, i.e. SO(2l+1), are in section VI, starting on page 69. The weights for the spin representation of $B_l$ are on page 70. An actual matrix form of the spin representation of $B_l$ might be given implicitly in section XV, on page 86. For $l=1$, it looks as though $X_1$ there might be $(1/2)(\sigma_1 + i \sigma_2)$, $X_{-1}$ might be $(1/2)(\sigma_1 – i \sigma_2)$, and $Y_1$ might be $\sigma_3$. But there does not seem to be any special discussion of the case $l=1$, or its relation to quaternions.
So for practical purposes, was the 2-dimensional representation of Hamilton’s quaternions actually unknown, until Pauli presented the Pauli matrices, in his paper “Zur Quantenmechanik des magnetischen Elektrons,” Zeitschrift für Physik, 43, 601–623, 1927?
John Goldman,
Unfortunately at this point I don’t know of a way to get generations out of twistor geometry.
Manuel del Rio Rodriguez,
I’ll be writing more about this here in coming months, but this year I’m teaching again the year-long course the book was based on. While doing this I’d like to revise and expand parts of the book, as well as make more minor improvements. I don’t think there will be big changes in the first part of the book during the fall semester, but I hope to make major changes in the second half, when I’m teaching in the spring semester.
Chris Austin, your comment intimates that Hamilton fell short in not achieving Pauli, when in fact the opposite is true. Pauli spinors are 2×1 complex matrices. The Pauli algebra, C(2), is isomorphic to the complexified quaternion algebra, the spinors of which are SU(2) doublets of Pauli spinors … so, had Pauli allowed Hamilton to inspire his work we may have had electro-weak U(1)xSU(2) theory a couple decades earlier than we did.
Chris Austin/Geoffrey Dixon,
The fact that the complexification of the quaternion algebra over the reals is the algebra of two by two complex matrices is something I’m sure Hamilton (and other algebraists later on) knew. But I think he was interested in quaternions as a remarkable real algebra, so not much interested in its obvious complex representations.
My own point of view is that physicists have a big blind spot in that they are used to just throwing in complex coefficients whenever convenient, so always work in a complexification and are blind to the fact that there may be multiple real forms of whatever algebra they’re working with. See my “two pet peeves” posting
https://www.math.columbia.edu/~woit/wordpress/?p=9222
I do think that removing this blind spot may help in better understanding the structure of fundamental physics, but there will be a lot, lot more needed to do this than keeping straight this simple example.
Speaking of lack of blogging, a couple of questions. Recently talk of the seriously suspect (bottom bins are even more suspect!) Xenon-axions experiment stuff is going around.
But we are supposed to be hearing from reliable, likely real, important (positive or negative, clarifying or muddying), results on neutrinos from several places, and muon g-2 experiments from Fermibab. We heard a bit on muon theory, very muddying.
Yet I see nothing blogged. Are there rumors or better? Even rumors of being bogged down whether for technical, analysis, or virus reasons?
Doug McDonald,
Sorry, but while I would love there to be some exciting experimental HEP news (or even a good rumor) to blog about, I haven’t heard any recently. Likely the COVID lockdown has impacted constructing and operating experiments, but people should still be able to analyze pre-COVID data from home…
You had me at non-spinning, non-sphere, but is the bottom line that despite the non-classical behavior of the wave function, it otherwise acts just like additional angular momentum?
Edward M. Measure,
To try and clarify the bottom line, yes, if you define
“angular momentum = observable that generates rotations”
Then, angular momentum can have two different sources
1. Effect of rotating $\vec{x}$ in $\Psi (\vec{x})$. This is the angular momentum you are used to, cause by “stuff moving around”, it’s “orbital angular momentum”, formula $$\vec{L}=\vec{x}\times \vec{p}$$
in its classical and quantum versions.
2. $\Psi$ may take values in a vector space on which rotations act non-trivially. Then when you rotate a wave function, you get a second contribution from this, the “spin angular momentum”. In the case of spin-half, $\Psi$ takes values in $\mathbf C^2$, the spinors, and rotations act on the spinors (in a new way unlike the normal action of rotation on vectors and tensors, including the fact that it is a double-cover of the rotation group that acts, the usual rotations act only up to minus-sign problems).
Hi Peter,
I enjoyed your post.
I’m just curious to know what do you think about the recent conference at the Perimeter Institute?
Thanks.
Babak,
I don’t want to start a discussion of quantum gravity here. For one thing, I don’t think there is anything new to say, and this has been true for quite a while. If you want an overview of the state of the subject I’d recommend looking at Nicolai’s talk. It seemed to me rather discouraging, with nothing like a promising new idea. The current philosophy that appears to be dominant is that quantum gravity is “emergent”. But Nicolai asks the right question: emergent from WHAT? And that’s a question with no good answer. He asks for experimental evidence to help with the situation, but gives no reason to believe such evidence will ever be available.
Peter woit,
you write about an entity that is represented in spinor form:
“If one finds a state with J_z = 1/2, rotating it by an angle 2*pi changes its sign. This is weird, but the sign of a state isn’t itself something you can measure.”
I think among the sources I’ve read you are the first one to write _explicitly_: “the sign of a state isn’t itself something you can measure”.
(Many sources state the following about entities represented in spinor form: “In order to return this object to the same state you have to turn it through 720 degrees.” without mentioning whether that is _observable_.)
I assume the spinor representation offers the most economical way (in mathematical sense) to reproduce the observed atomic spectrum energy levels.
Let me make a comparison: in electronic engineering it is common to move the mathematical representation to complex number space, so that the equations are not in the form of sines and cosines, but exponential functions, allowing much more efficient manipulation of occurences of phase shift. It’s a trade-off, you introduce imaginary voltage and imaginary current, and you get more efficient manipulation, but at the end of the computation you have to convert back to observables: measured voltage and measured current
Is it possible at all to interpret the spinor representation in a similar way? That is, that it is an economical representation, but at the expense of introducing an _unobservable_ property (“a state with J_z = 1/2, rotating it by an angle 2*pi changes its sign”)
The Einstein-De Haas effect
As is well known, the Einstein-De Haas effect drives home the point: if you manipulate the spin angular momentum of a sufficiently large population you can obtain exchange of a macroscopic amount of angular momentum.
https://www.youtube.com/watch?v=qFkW0PHhXcY
That is: I think it’s worth emphasizing:
quantummechanical spin angular momentum doesn’t have a classical counterpart, but not in the sense that it only exists in some confined environment. Exchange with macroscopic objects can be elicited.
Chris Austin/Geoffrey Dixon/Peter Woit,
I agree that using quaternions rather than Pauli matrices makes the concept of spin understandable in a more elegant way. “Throwing in” complex numbers does obscure some of the issues. But there is more than one way of throwing in complex numbers. From quaternions/SU(2) one can either go the Pauli route, and end up with SL(2,C), or the Glashow-Weinberg-Salam route, and end up with U(2), often erroneously described as U(1) x SU(2). More clarity on the difference between these methods of throwing in complex numbers, and the underlying reasons for them, would certainly help me to understand what is going on.
Dear Peter,
thank you for advertizing my talk at QG2020. It was, however, not meant to be discouraging at all! It is just that (as my father, a medical doctor, used to say) “diagnosis must precede therapy”. And part of the diagnosis is that low energy SUSY is clinically dead, that the multiverse program is unlikely to get anywhere, and (for the “non-string approaches”) that explaining this or that particular feature of (say) the CMB is by far not enough, especially if you cannot clearly discriminate your explanation from other competing ones (after all, it might just be dust…). Last but not least divergences between different approaches are still so substantial that hope for a “grand syntesis” is far away. So the PI people did a great job in bringing together all these viewpoints and making the proponents talk to one another, and from that point of view the conference was a great success.
In the end it will only work if everything fits together, and a key element of this is explaining how the standard model (as is!) can emerge from a Planck scale theory. On this we have some ideas of our own (see my last two slides), but I did not want to overly emphasize this as (1) we might well be wrong, and (2) it is not the main purpose of an overview talk to push one’s own pet ideas.
Best regards,
Hermann
Regarding the explanation of why the standard model is as it is, I noticed than neither in the opening talk by Nicolai nor the closing one by Jacobson there is any mention of Connes and al approach to the SM using noncommutative geometry, although there have been various developments in the last years.
This might well be because this is not a theory of quantum gravity, and so it was not strictly in the scope of the conference. However this is a bit surprising because there are some people working on that topic at PI.
Is this approach to the SM so much “out of the radar” for physicist ? (I am asking without polemical intention, I am genuinely interested in understanding why it seems so much ignored ?).
Cleon Teunissen,
The comment that the minus sign for spin causes no immediate problem because it is a sign of a wave-function, not of an observable certainly isn’t original to me. Discussing this gets into the interpretational issue of the physical significance of the wave-function, which is a discussion I very much don’t want to start again here.
On the analogy to solving real-valued problems with complex numbers: what’s going on there essentially is that, given a problem with a real-valued solution, you can ask for complex solutions, allowing use of the properties of complex numbers, making finding solutions easier. If you find a complex solution, you have found two solutions to your original problem (the real and imaginary parts), although one may be zero.
What’s happening with spinors is different. There is a serious question about whether it’s best to describe them in terms of real numbers, complex numbers, or quaternions, but the underlying fact is that there is a new and different spin-1/2 degree of freedom, which is undeniably there. It’s not something you are introducing just for calculational convenience.
martibal and all,
I’m glad to have pointed those interested to Nicolai’s interesting review, and happy that he added comments here, but, as usual, I don’t want to start here an open-ended discussion of the state of speculative ideas, whether about non-commutative geometry or anything else.
I expect you already know this, Peter, but there is also a classical version of spin-1/2. It’s a little subtler than integer angular momentum, but works just as well. This a charge on a sphere in the presence of a static monopole. This yields a Wess-Zumino action for the unit vector (or element of S^2), and upon quantization, this vector’s components become the Pauli matrices. A more general model (due to Tamm) is a charge anywhere in R^3, in the presence of a static monopole at the origin (which has wave functions which change sign under a rotation).
There is even a nice relativistic generalization. This is a slightly more complicated Wess-Zumino term, depending on two unit vectors in $R^4$, one of which is parallel to the four velocity, and the other which is orthogonal to the first (so the configuration space is $S^3\times S^3/U(1)$. This gives Dirac fermions after quantization (in Euclidean space. To get to Minkowski space, the $S^3$’s must be replaced by hyperboloids). One vector is the velocity divided by its norm. When quantized, this vector’s components become the Dirac gamma matrices. The other unit vector’s components become the rho matrices.
Thanks Peter,
That’s a interesting physical variant of the general idea of taking $S^2$ as phase space and quantizing, but using the monopole to give the quantization line bundle.
I realized there’s another way to think of this, to argue that the spin-1/2 degree of freedom is what you get when you look not at classical mechanics, but at pseudo-classical mechanics (your phase space variables are anti-commuting) in the simplest non-trivial (d=3) case. I wrote up the details of this in chapter 30 and 31 of the book on QM (http://www.math.columbia.edu/~woit/QMbook/qmbook.pdf).
Hi Peter,
Are you sure that geometric quantization isn’t the best way to understand the spinor degree of freedom? It seems like a good way to go, based on a lower-dimensional example. Quantize space with a honeycomb lattice, and spin 1/2 pops right out. See this paper in Physical Review Letters: https://arxiv.org/abs/1003.3715.
Chris Regan,
There are lots of ways to get a spinor degree of freedom out of a much more complicated structure. But spinors are really an extremely simple story about two by two matrices. What I’d like to advertise is this simplicity. If you want the simplest possible way to explain where spinors come from, twistor geometry is very compelling, giving spinors tautologically (a point in space time is exactly the spinor space).