Research
-
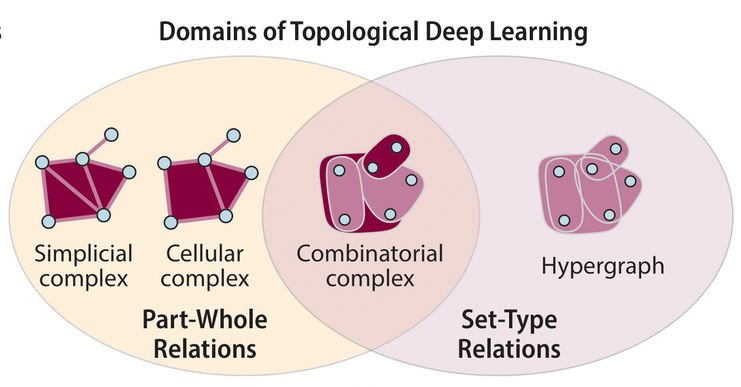
ICML Topological Deep Learning Challenge 2024: Beyond the Graph
Domain
-
Universal Strict Lifting
Lifting from the hypergraph domain to the combinatorial complexes domain. The lifting is strict universal, which means that any other lifting which produces a strict combinatorial complex is a composition of our lifting and another mapping. Awarded an honorable mention at ICML 2024.
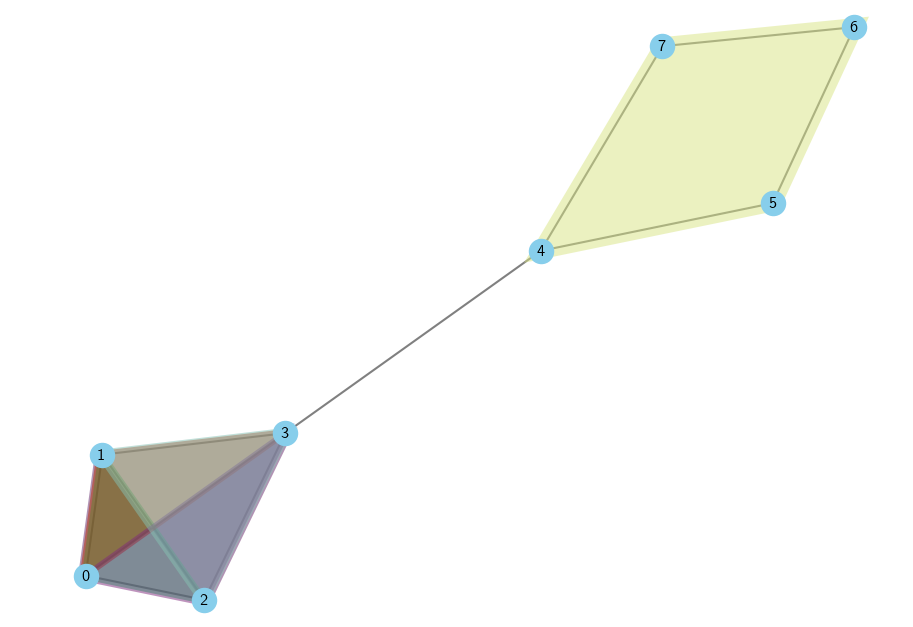
-
Probabilistic Clique Lifting
Lifting from the graph domain to the combinatorial complexes domain. The lifting is suited to situations with missing edge data, where it is assumed that edges have been erased randomly and uniformly. It uses a probabilistic threshold to add higher-order cliques to the lifting, even when part of the clique is missing.
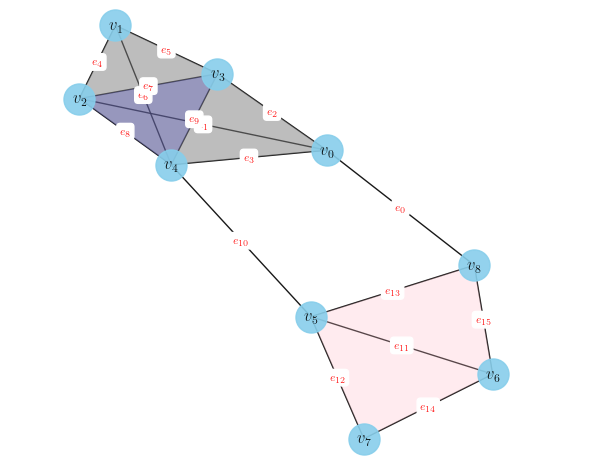
-
Universal Strict Lifting
-
A new modular plethystic
\(\mathrm{SL}_2(\mathbb{F})\)-isomorphism
Joint with Mark Wildon. Let \( \mathbb{F} \) be a field and let \( E \) be the natural representation of \( \mathrm{SL}_2(\mathbb{F}) \). Given a vector space \( V \), let \( \Delta^{(2,1^{N-1})}V \) be the kernel of the multiplication map \( \wedge^N V \otimes V \to \wedge^{N+1} V \). We construct an explicit \( \mathrm{SL}_2(\mathbb{F}) \)-isomorphism \[ \mathrm{Sym}^{N-1} E \otimes \wedge^{N+1} \mathrm{Sym}^{d+1} E \cong \Delta^{(2,1^{N-1})} \mathrm{Sym}^d E. \] This \( \mathrm{SL}_2(\mathbb{F}) \)-isomorphism is a modular lift of the q-binomial identity \[ q^{N(N-1)/2} [N]_q \binom{d+1}{N+1}_q = s_{(2,1^{N-1})}(1, q, \ldots, q^d), \] where \( s_{(2,1^{N-1})} \) is the Schur function for the partition \( (2, 1^{N-1}) \). This identity, which follows from our main theorem, implies the existence of an isomorphism when \( \mathbb{F} \) is the field of complex numbers but it is notable, and not typical of the general case, that there is an explicit isomorphism defined in a uniform way for any field.
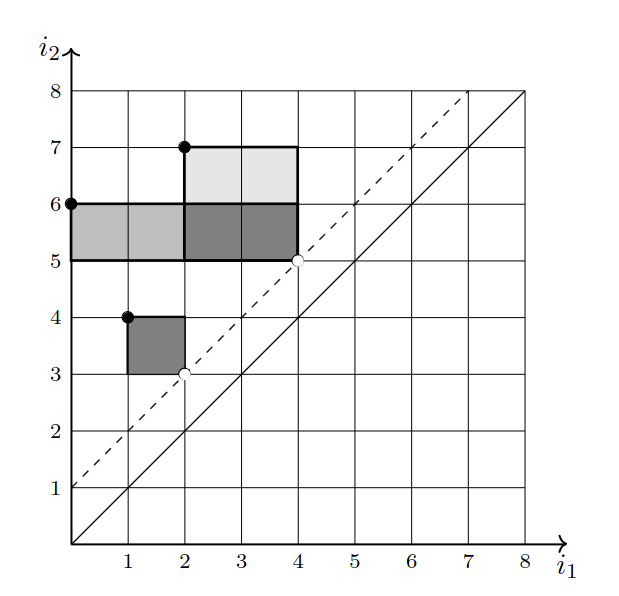
-
Foams Python package
Foam evaluation is the key ingredient in the most modern formulation of Khovanov-Rozansky homology for knots and links, by Robert and Wagner. We introduce a novel implementation of the Robert-Wagner coloring formula for foams. Our implementation is completely general: it admits any number of colors for a foam in any given position in space. The coloring algorithm is feasible up to \(N=10\) colors, an improvement over the naive backtracking algorithm, which is only feasible up to \(N=4\) colors even for small foams (\(10\) facets). Our approach consists in translating coloring enumeration into an Integer Linear Programming problem.
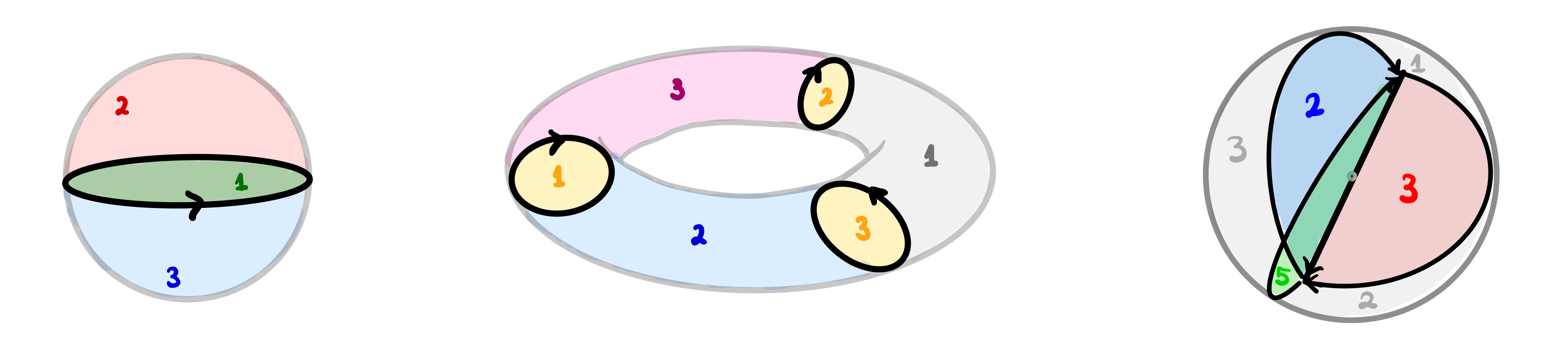
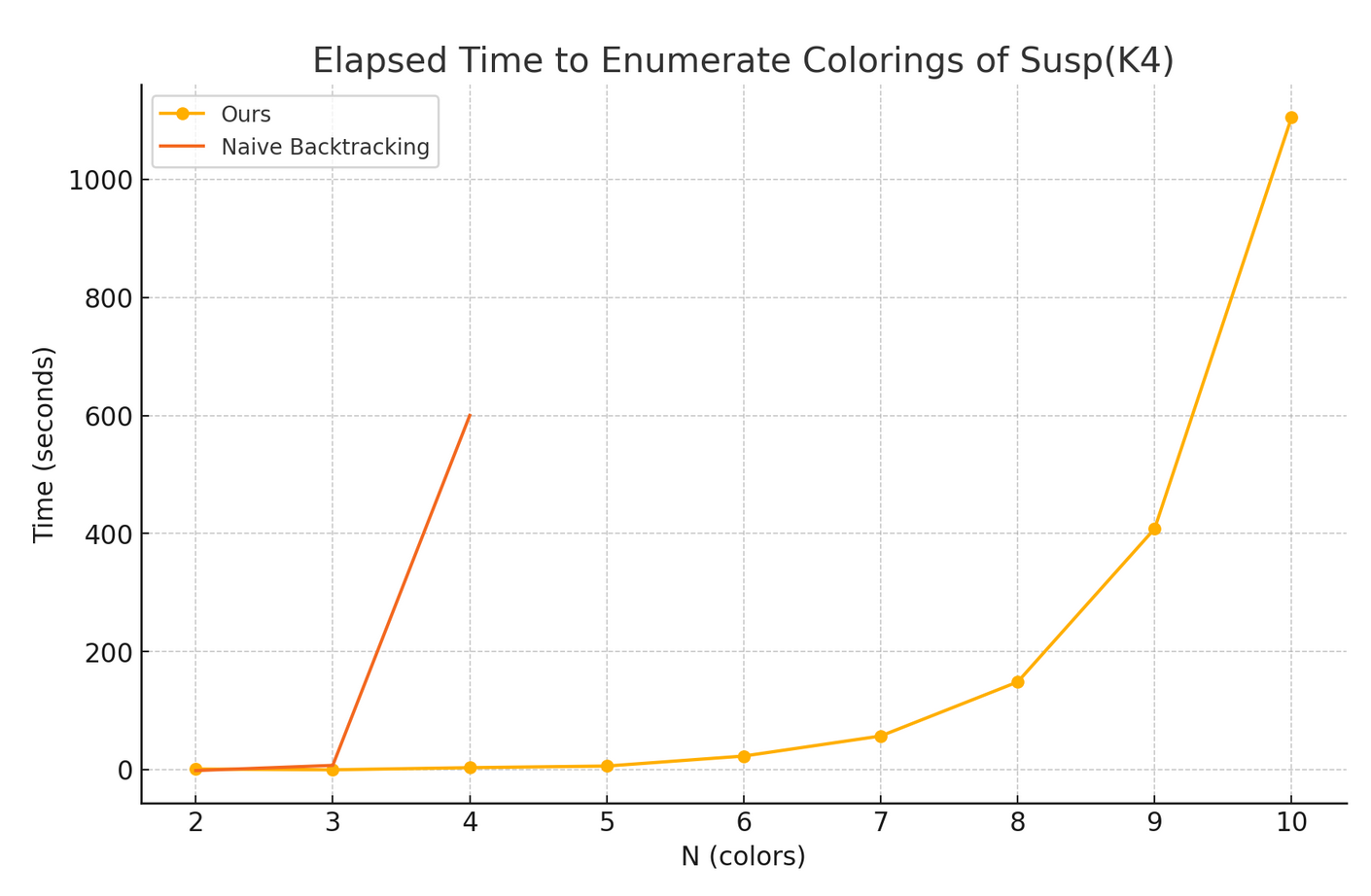
-
Low-dimensional irreducible rational representations of classical
algebraic groups
Let \( G \) be an algebraic group of classical type of rank \( l \) over an algebraically closed field \( K \) of characteristic \( p \). We list and determine the dimensions of all irreducible \( KG \)-modules \( L \) with \(\dim L < \frac{(l+1)}{4}\) if \( G \) is of type \( A_l \), and with \(\dim L < 16\left(\frac{l}{4}\right)\), if \( G \) is of type \( B_l \), \( C_l \) or \( D_l \).

-
Small-dimensional representations of algebraic groups of type
\(A_l\)
For \( G \) an algebraic group of type \( A_l \) over an algebraically closed field of characteristic \( p \), we determine all irreducible rational representations of \( G \) in defining characteristic with dimensions \(\leq (l+1)s\) for \( s = 3, 4 \), provided that \( l > 18 \), \( l > 35 \) respectively. We also give explicit descriptions of the corresponding modules for \( s = 3 \).
