Foams Python Package

I have developed a Sage class for foams, colorings, and Robert-Wagner evaluation. See it on GitHub

What is a foam?

Motto: Surfaces are to circles as foams are to trivalent graphs.

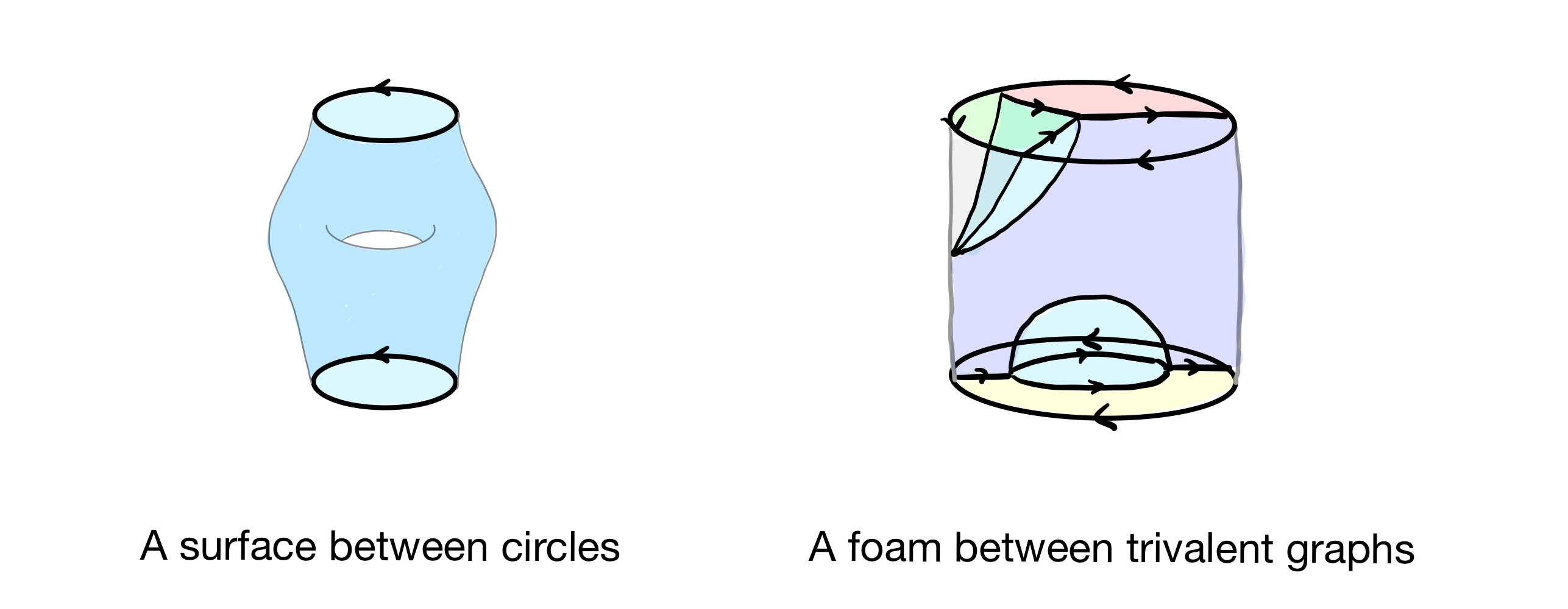
An example of a foam

Just like a surface locally looks like a plane, a foam locally looks like one these:

A foam looks locally like a surface, a binding, or a singular vertex

They are called foams because they kind of resemble soap bubbles coming together.

Actual real life foam

Here are some examples:

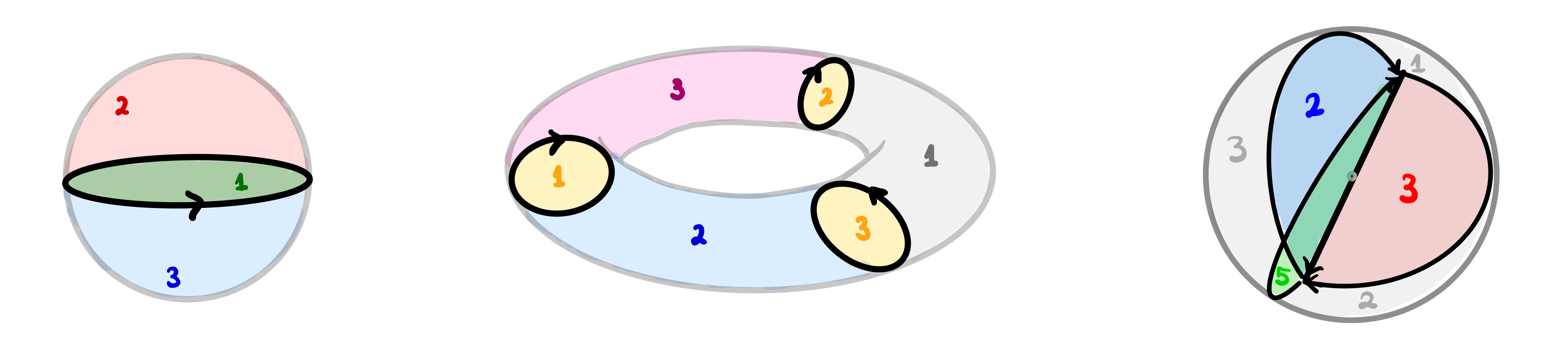
Three examples of foams

The first one is called the theta foam: if you look at it from the side it resembles the greek letter θ

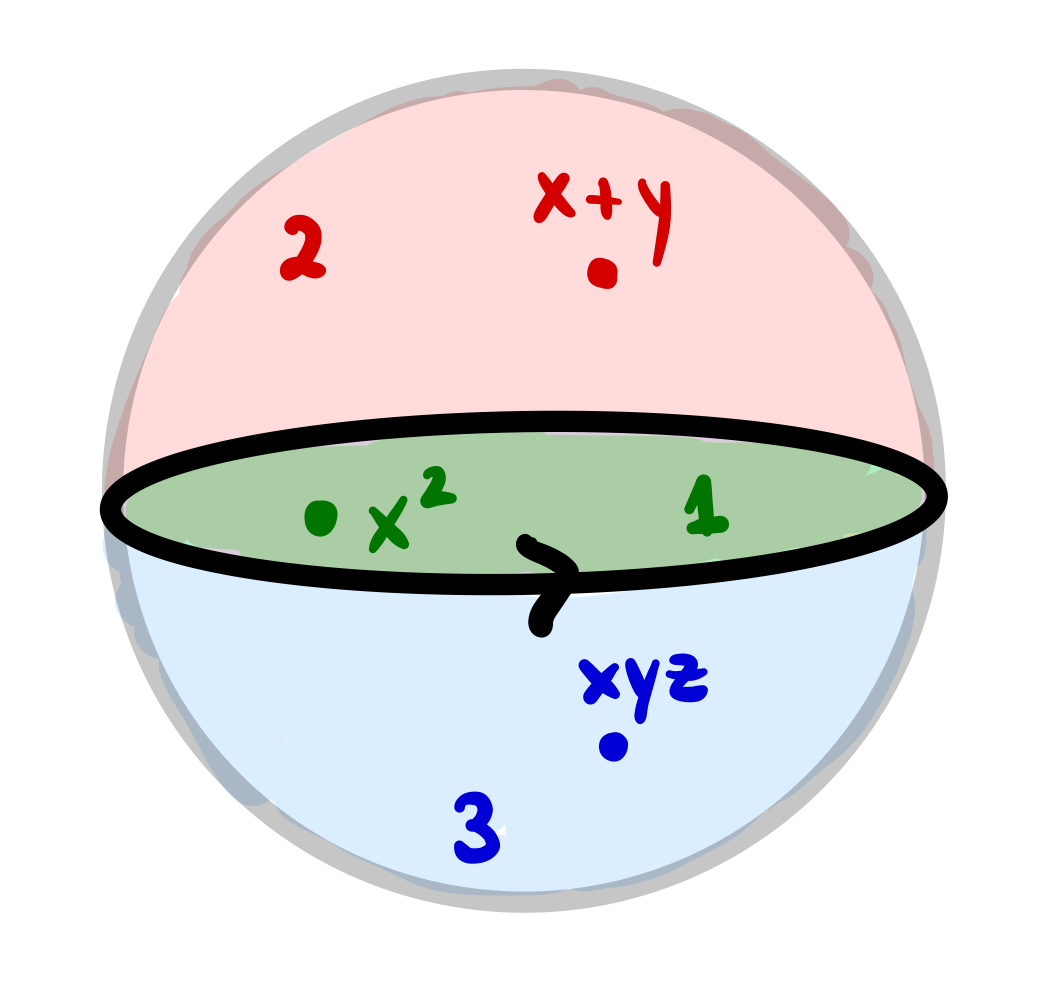
Notice that (mathematical) foams have integers on their faces. These are called thicknesses. They may also have polynomials on the facets:

A decorated theta foam

What this package does

The new Foam class allows you to define such foams. For the example above, all we need to do is define a SimplicialComplex representing the theta foam, and assign thicknesses, decorations, and the orientation around the binding:

# Foam facets
two_cells = [[0,1,2],[0,1,3],[0,2,3],[1,2,3],[1,2,4],[1,3,4],[2,3,4]]
# Polynomial decorations and orientation around the binding
decorations = [[2], [2], [1,1]]
orientations = [[1]]
theta_complex = SimplicialComplex(two_cells)
F_theta = Foam(theta_complex, thicknesses, decorations, orientations)
F_theta
Foam with Simplicial complex with vertex set (0, 1, 2, 3, 4) and 7 facets, with 3 foam facets, 1 binding and 0 singular points.

For graphs, there is a notion of graph colorings. Robert and Wagner proposed a notion of a foam coloring. Here is an example:

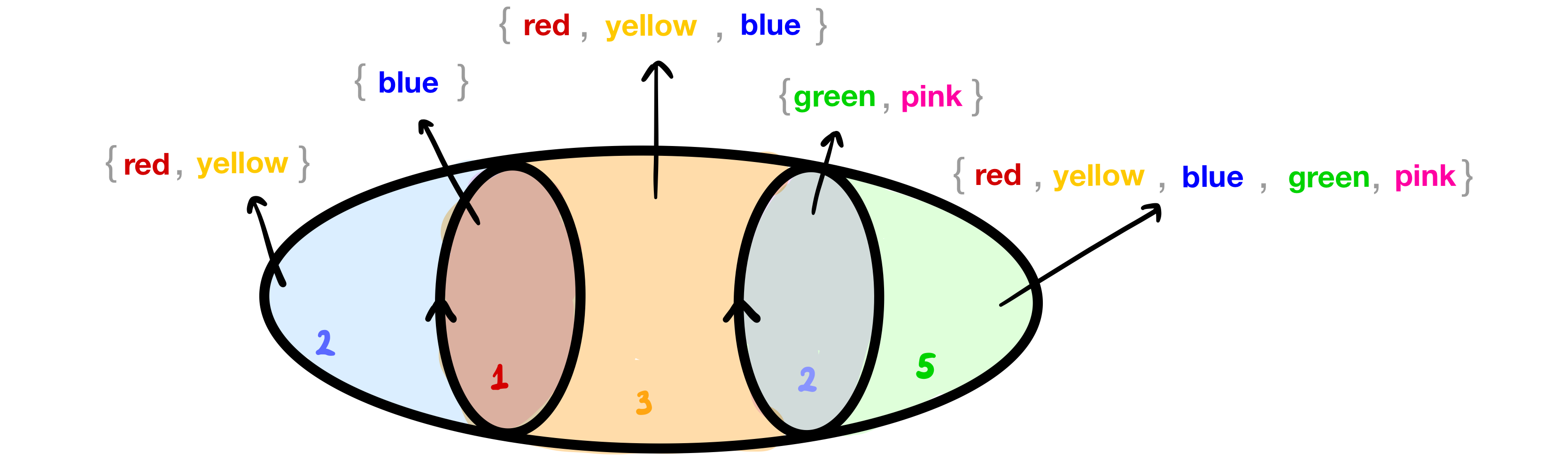
A foam with a coloring

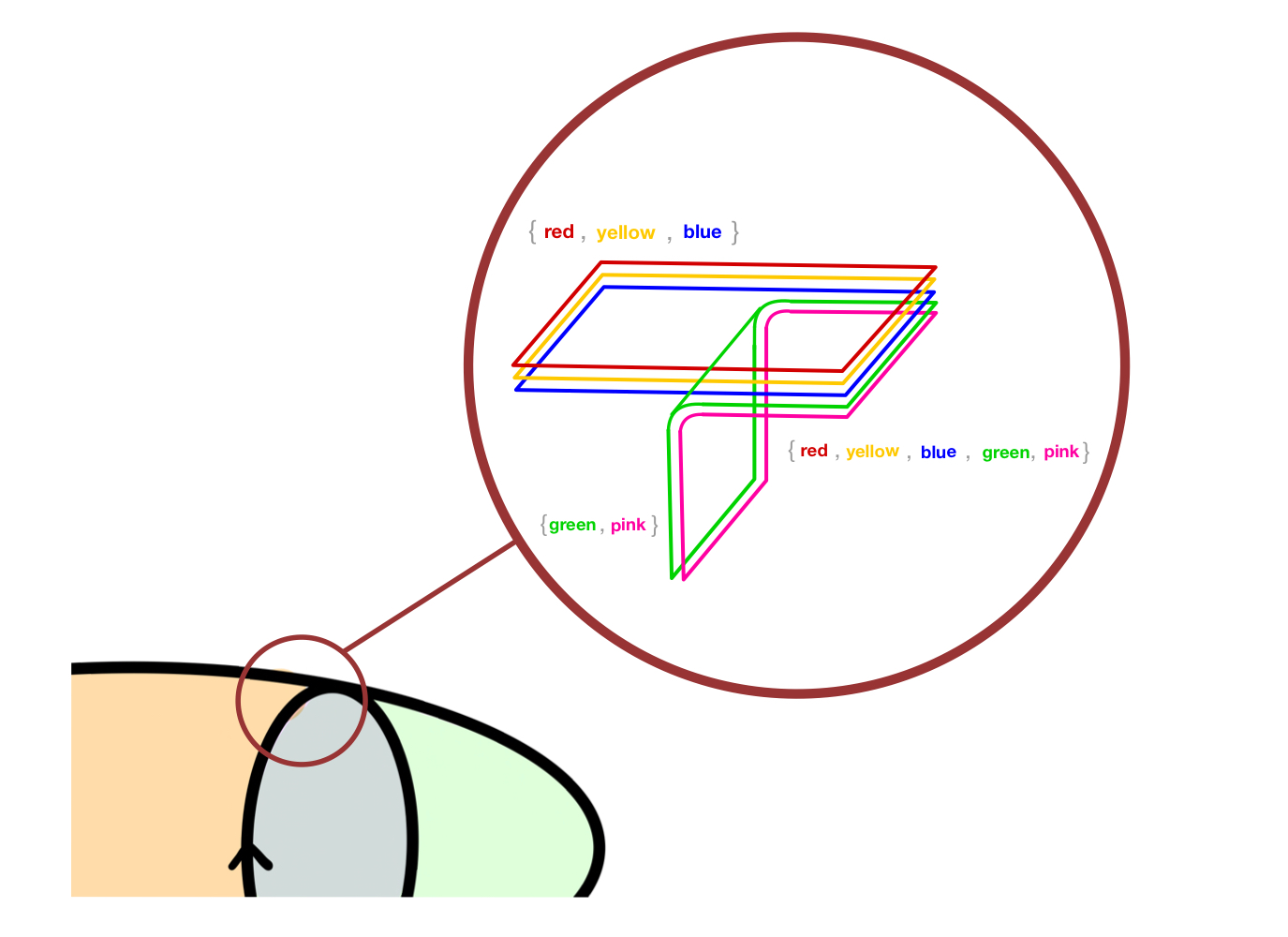
Notice that a facet of thickness t has exactly t colors, and two facets coming together into a third satisfy a "flow condition":

The flow condition for foams

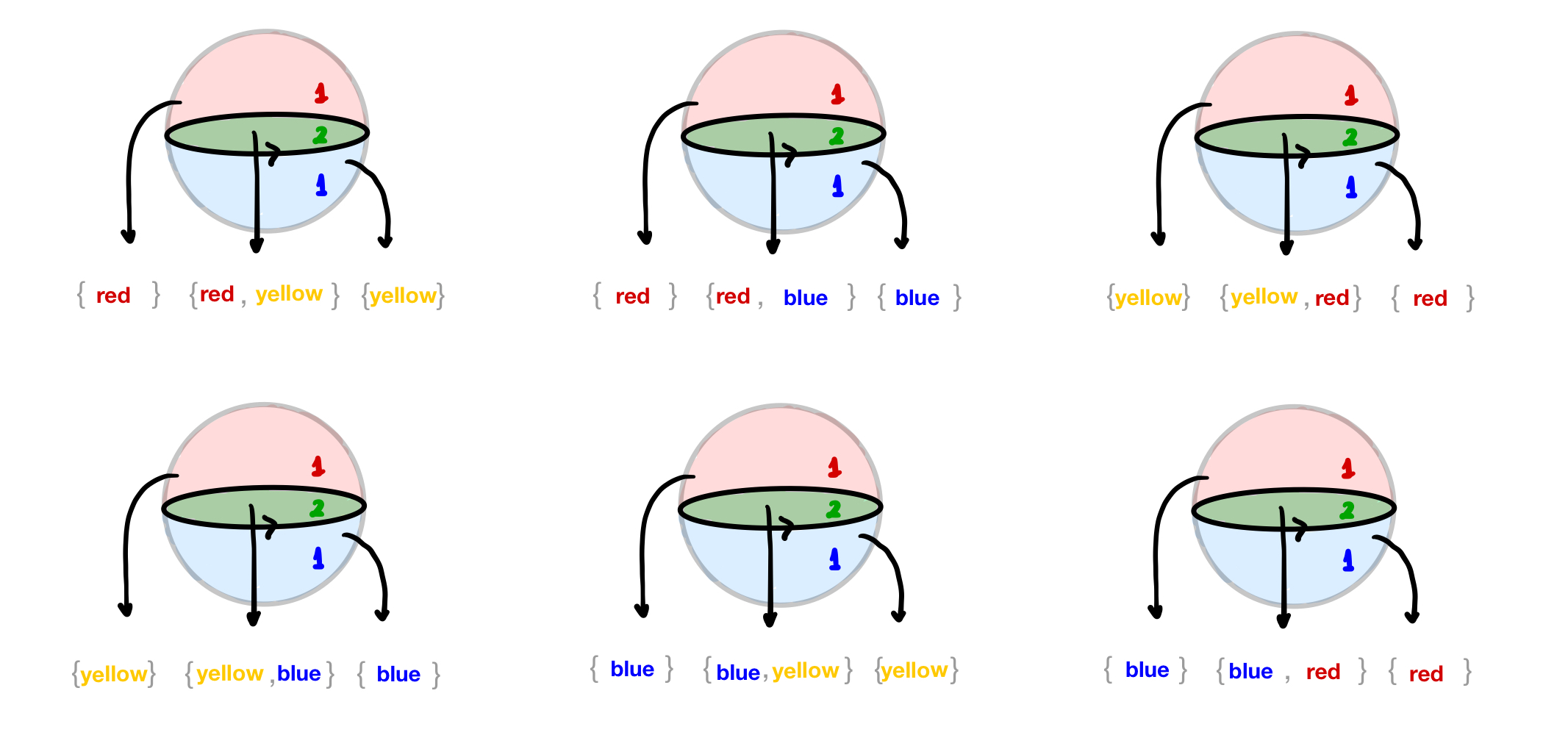
The Foam class has a method to enumerate colorings using N colors. For example, the following foam has 6 colorings using three colors (red, yellow, blue):

Enumerating colorings of a foam in Sage

We can easily get these colorings on Sage:

theta_foam = foams.ThetaFoam(thicknesses = [1, 2, 1])
display(theta_foam.colorings(3))
[[[0], [0, 2], [2]],
[[0], [0, 1], [1]],
[[1], [1, 2], [2]],
[[1], [0, 1], [0]],
[[2], [1, 2], [1]],
[[2], [0, 2], [0]]]

Robert and Wagner defined an evaluation formula that takes a foam and a coloring and it gives a quotient of polynomials, for instance:

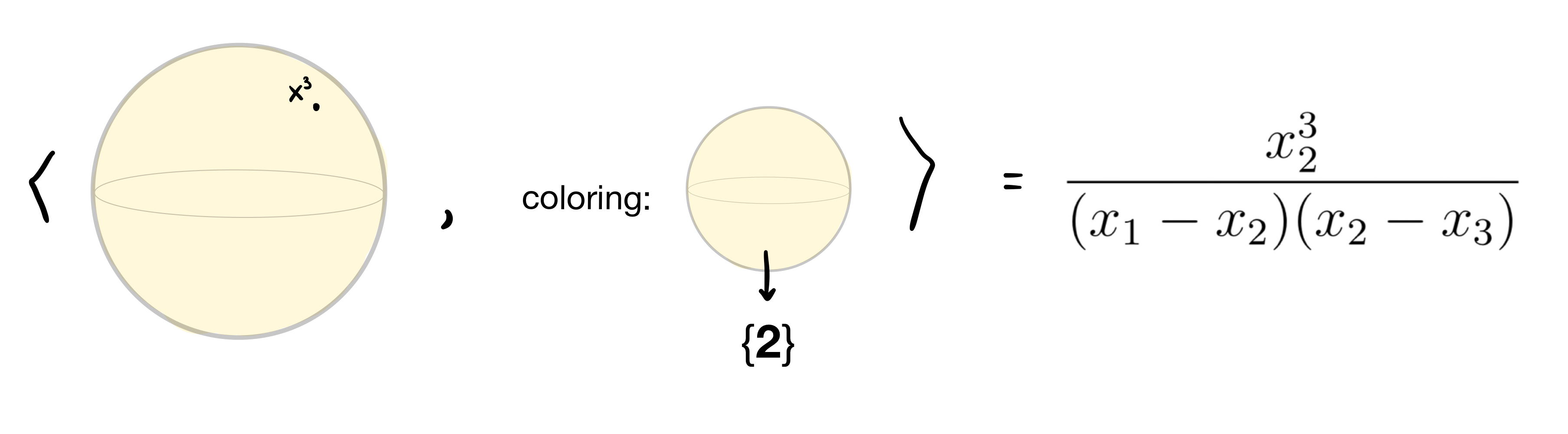
The evaluation of a sphere of thickness 1 with a coloring

Adding all of the contributions for each coloring of a foam should yield a quotient of polynomials. One of the miraculous properties of this evaluation is that, in fact, it returns polynomials:

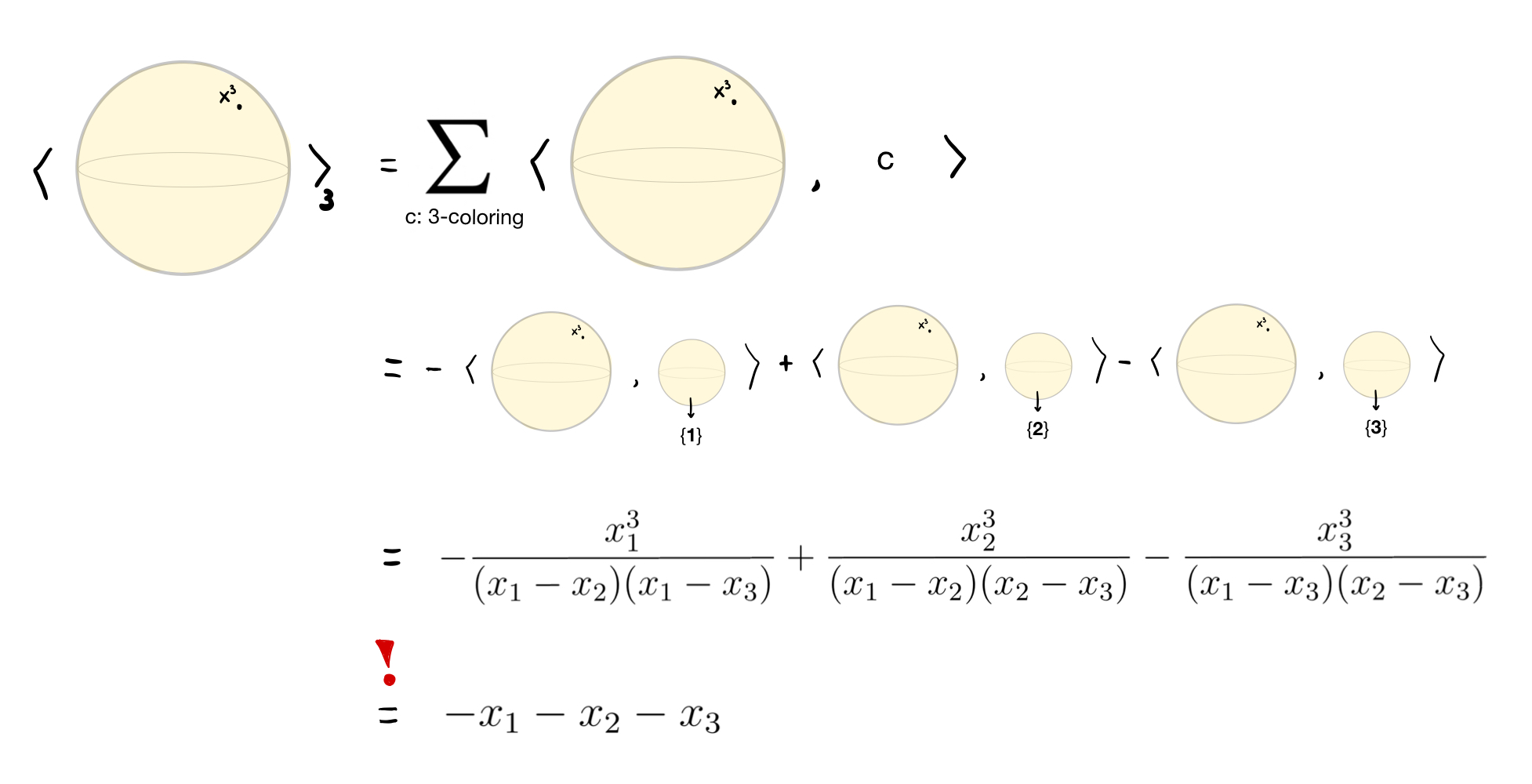
The evaluation of a foam is actually a polynomial

We can confirm this in Sage:

sphere_foam = foams.SphereFoam(thicknesses = [1], decorations = [[3]])
sphere_foam.RW_evaluation(3)
-x0 - x1 - x2

Efficient coloring enumeration

Previous implementations of the Robert-Wagner formula struggled with as few as 4 colors and a few facets. Our new approach transforms the foam coloring problem into an Integer Linear Programming (ILP) problem, which allows us to find colorings with up to 9 colors if the foams are not too large. Take the following foam:

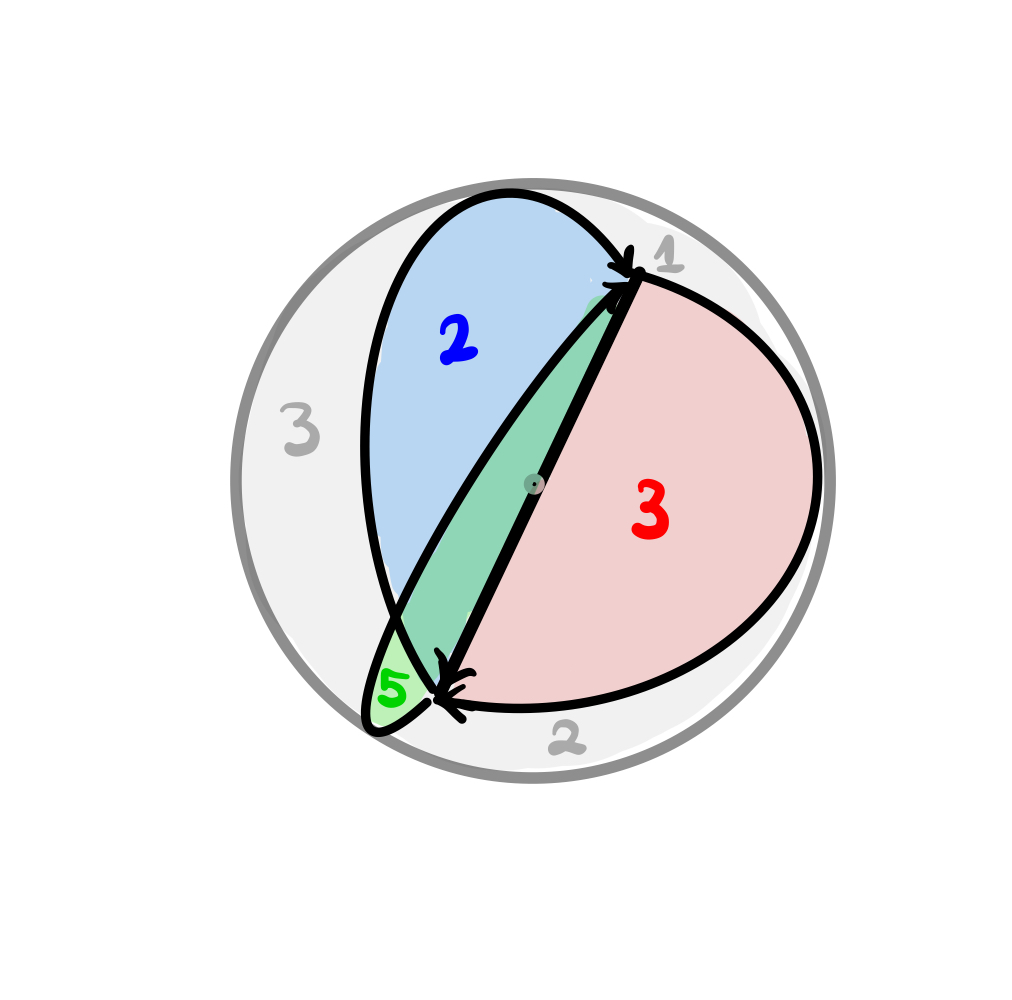
A more complicated foam

Let's define it in Sage and find its colorings using 9 colors:

suspK4 = foams.SuspensionK4(thicknesses = [2, 1, 3, 3, 2, 5])
print(len(suspK4.colorings(9)))
display(suspK4.colorings(9))
3780
[[[2], [1, 2, 8], [0, 3], [1, 8], [0, 2, 3], [0, 1, 2, 3, 8]],
[[2], [1, 2, 7], [0, 3], [1, 7], [0, 2, 3], [0, 1, 2, 3, 7]],
[[2], [1, 2, 6], [0, 3], [1, 6], [0, 2, 3], [0, 1, 2, 3, 6]],
...

The ILP solver finds a single coloring each time, but then the algorithm excludes that single coloring and calls the ILP solver again. Since there are relatively few colorings, the time complexity comes down to the complexity of the ILP solver, which is highly optimized.

Early access

If you would like early access to this package (which contains other features, such as constructor methods and a foams catalog), please contact me.