Since the last update we have worked on examples of stacks, stack of torsors, quotients stacks [X/G], Picard stack, epimorphisms of rings, change of partial universe for algebraic spaces, Gabriel-Zisman localization, pushforward of stacks, pullback of stacks, change of partial universe for algebraic stacks, change of base scheme for algebraic stack, and finally we started working on a new chapter entitled Properties of Algebraic Stacks.
As you can see from the list, we worked through a lot of very formal material. Some of this is a bit rough as written, although almost all of it is “obviously correct”. This is OK as at least some of it is just meant to explain set theoretical issues.
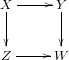
But now we’ve finally caught up with this material and we can start working on algebraic stacks! Moreover, I have decided to introduce the customary abuse of language in the first section of the new chapter linked to above. The idea is that any confusion which is caused by this abuse of language should be explained by pointing to a lemma in Algebraic Stacks or earlier. For example, we will say that an algebraic stack is an algebraic space if it is representable by an algebraic space (which is equivalent to have trivial inertia stack, see Proposition Tag 04SZ). Then suppose X, Y, Z, W are algebraic stacks and we are given a diagram
and X, Y, Z, W “are” algebraic spaces. What does it mean to say “the diagram is commutative” or “the diagram is cartesian”? Well, it could either mean that the diagram is a commutative, resp. cartesian in the category of algebraic spaces, or that the diagram is 2-commutative, resp. a 2-fibre product diagram in the 2-category of algebraic stacks. The abuse of language is not confusing in this case since these conditions agree. More precisely: the diagram is 2-commutative if and only if the corresponding diagram of sheaves of isomorphism classes of objects of fibre categories is commutative, and the diagram is a 2-fibre product if and only if the corresponding diagram of sheaves of isomorphism classes of objects of fibre categories is cartesian.

Hi Johan. Davesh Maulik were talking about stacks recently, and the following property of stacks came up: the stack is finitely presented and smooth over a field and has a stratification by locally closed substacks which are “global quotient stacks”. This property holds for the stack of prestable curves, for instance (where the stratification is by topological type). Do you know if this property implies that the stack is a quotient stack?
Typo correction: “Davesh Maulik were” –> “Davesh Maulik and I were”.
Pingback: Update « Stacks Project Blog