In his classical paper [1], Deuring proved the following refined result concerning the endomorphism rings of elliptic curves (and much more).
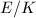 be an elliptic curve with
be an elliptic curve with 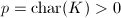 .
.
- If the endomorphism algebra
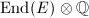 is an imaginary quadratic field
is an imaginary quadratic field 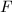 , then
, then 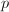 splits in
splits in 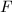 and
and 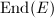 is an order in
is an order in 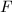 of conductor prime to
of conductor prime to 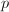 . Conversely, all such orders occur as endomorphism rings.
. Conversely, all such orders occur as endomorphism rings. - If
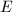 is supersingular, then
is supersingular, then 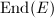 is a maximal order in the unique rational quaternion algebra ramified only at
is a maximal order in the unique rational quaternion algebra ramified only at 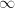 and
and 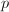 . Conversely, all such orders occur as endomorphism rings.
. Conversely, all such orders occur as endomorphism rings.
In this chapter, we will prove part of Deuring's theorem. Namely, we will prove that the endomorphism ring of a supersingular elliptic curve over a finite field is an maximal order in the rational quaternion algebra ramified only at 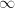 and
and 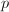 , using an approach different from Deuring's original proof. Our argument of the maximality comprises two major parts. On the
, using an approach different from Deuring's original proof. Our argument of the maximality comprises two major parts. On the 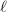 -part,
-part,  can be identified with the endomorphisms of the
can be identified with the endomorphisms of the 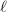 -adic Tate module. On the
-adic Tate module. On the 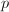 -part,
-part, 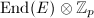 can be identified with the endomorphisms of the formal group
can be identified with the endomorphisms of the formal group 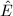 .
.
We will begin with giving a criterion for endomorphism rings in terms of the heights of the formal groups. Next, we will discuss several interesting properties of quaternion algebras. By utilizing the nontrivial results of Tate and Dieudonné-Lubin, we will be able to achieve our goal mentioned above. Finally, two sections will be devoted to a short discussion of abelian varieties and Tate's isogeny theorem.
 Endomorphism rings and heights
Endomorphism rings and heights
As promised in the first chapter, we will first connect the supersingularity with the 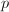 -torsion part of an elliptic curve. We mainly follow [2] in this section.
-torsion part of an elliptic curve. We mainly follow [2] in this section.
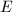 be an elliptic curve over
be an elliptic curve over  with
with 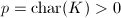 . Denote the
. Denote the  -th Frobenius map by
-th Frobenius map by 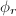 . Then the following are equivalent:
. Then the following are equivalent:
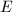 is supersingular.
is supersingular.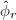 is purely inseparable for one (all)
is purely inseparable for one (all) 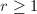 .
.![$[p]$](./latex/latex2png-MinorThesis2_2132972_-5.gif) is purely inseparable and
is purely inseparable and 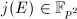 .
.![$E[p^r]=0$](./latex/latex2png-MinorThesis2_19604469_-5.gif) for one (all)
for one (all) 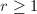 .
.
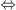 (d) Since
(d) Since  -Frobenius maps are purely inseparable ([2, II 2.11]), we know that
-Frobenius maps are purely inseparable ([2, II 2.11]), we know that ![$$\# E[p^r]=\# \ker [p^r]=\deg_s[p^r]=\deg_s \hat\phi_r, \quad r\ge1.$$](./latex/latex2png-MinorThesis2_184573240_.gif) Hence the equivalence of (b) and (d) follows.
Hence the equivalence of (b) and (d) follows.
(a) (b) Suppose
(b) Suppose 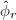 is separable for all
is separable for all 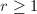 , then
, then ![$\# E[p^r]=p^r$](./latex/latex2png-MinorThesis2_220440143_-5.gif) . Consider the natural map
. Consider the natural map  , then
, then  is injective in this case. That is because if
is injective in this case. That is because if 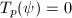 for some
for some 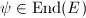 , then
, then ![$\psi(E[p^r])=0$](./latex/latex2png-MinorThesis2_254960562_-5.gif) , hence
, hence 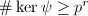 for all
for all 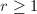 , which implies
, which implies 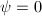 since nonconstant isogeny has finite kernel. Now
since nonconstant isogeny has finite kernel. Now 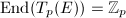 is commutative and the map
is commutative and the map  is injective, so
is injective, so 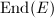 must be commutative.
must be commutative.
(b) (c) Let
(c) Let 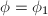 be the
be the 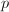 -Frobenius map. Since
-Frobenius map. Since ![$[p]=\hat\phi\circ\phi$](./latex/latex2png-MinorThesis2_236737869_-5.gif) and
and 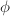 is purely inseparable, if
is purely inseparable, if 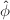 is purely inseparable, then so is
is purely inseparable, then so is ![$[p]$](./latex/latex2png-MinorThesis2_2132972_-5.gif) .
.
Because 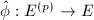 is purely inseparable, it factors through the
is purely inseparable, it factors through the 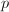 -Frobenius map
-Frobenius map 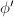 on
on 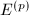 , namely
, namely 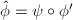 where
where 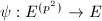 is an isomorphism. Therefore
is an isomorphism. Therefore 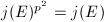 , which means
, which means 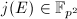 .
.
(c) (a) Under condition (c), we claim that there are only finitely many elliptic curves that are isogenous to
(a) Under condition (c), we claim that there are only finitely many elliptic curves that are isogenous to 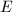 . Suppose
. Suppose 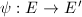 is an isogeny. Since the isogeny
is an isogeny. Since the isogeny ![$[p]$](./latex/latex2png-MinorThesis2_2132972_-5.gif) on
on 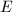 is purely inseparable and
is purely inseparable and ![$[p]\circ\psi=\psi\circ[p]$](./latex/latex2png-MinorThesis2_41474622_-5.gif) , we know that the isogeny
, we know that the isogeny ![$[p]$](./latex/latex2png-MinorThesis2_2132972_-5.gif) on
on 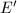 is also purely inseparable. So
is also purely inseparable. So  . There are only finitely many
. There are only finitely many  -invariants for
-invariants for 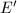 , hence the claim follows.
, hence the claim follows.
Now suppose 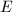 is not supersingular, then
is not supersingular, then 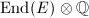 is either
is either 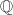 or an imaginary quadratic extension of
or an imaginary quadratic extension of 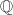 . Since there only finitely many
. Since there only finitely many 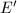 that is isogenous to
that is isogenous to 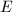 , we can find a prime
, we can find a prime 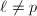 such that
such that 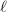 remains a prime in each
remains a prime in each 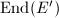 . Since
. Since ![$E[\ell^n]=\mathbb{Z}/\ell^n\mathbb{Z}\times\mathbb{Z}/\ell^n\mathbb{Z}$](./latex/latex2png-MinorThesis2_133362037_-5.gif) by Theorem 2, we can find a sequence of cyclic groups
by Theorem 2, we can find a sequence of cyclic groups 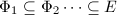 satisfying
satisfying 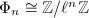 . Using [2, III 4.12], we get a separable isogeny
. Using [2, III 4.12], we get a separable isogeny 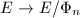 with kernel
with kernel  . By the claim above again, there exist some positive integers
. By the claim above again, there exist some positive integers 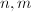 such that
such that 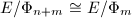 . Now the natural map
. Now the natural map 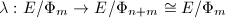 has degree
has degree 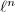 and has kernel
and has kernel 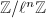 . Since
. Since  is a prime in
is a prime in 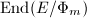 , comparing degrees we obtain
, comparing degrees we obtain ![$\lambda=\psi\circ[\ell^{n/2}]$](./latex/latex2png-MinorThesis2_80088381_-5.gif) where
where 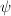 is an isomorphism. But the kernel of
is an isomorphism. But the kernel of ![$[\ell^{n/2}]$](./latex/latex2png-MinorThesis2_137881675_-5.gif) is not cyclic, a contradiction.
¡õ
is not cyclic, a contradiction.
¡õ
The following theorem connects the inseparable degree of an isogeny with the height of the associated map of formal groups in positive characteristic. Combining it with Theorem 2, we will be able to give a characterization of endomorphism rings in terms of the height of the formal group (Theorem 4).
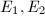 be two elliptic curves over
be two elliptic curves over  with
with 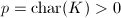 . Let
. Let 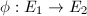 be an isogeny and
be an isogeny and 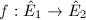 be the associated homomorphism of formal groups. Then the inseparable degree
be the associated homomorphism of formal groups. Then the inseparable degree 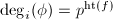 , where
, where 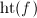 is the height of the homomorphism
is the height of the homomorphism  .
.
Suppose 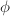 is the
is the  -Frobenius map, then
-Frobenius map, then 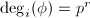 . On the other hand, the associated homomorphism
. On the other hand, the associated homomorphism 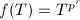 , so
, so 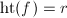 .
.
Suppose 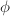 is a separable map, then
is a separable map, then 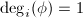 and
and 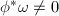 , where
, where 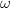 is the invariant differential. So as a differential on formal group
is the invariant differential. So as a differential on formal group 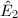 , we have
, we have 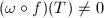 . But
. But 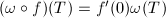 ([2, IV 4.3]), it follows that
([2, IV 4.3]), it follows that 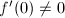 , therefore
, therefore 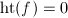 .
¡õ
.
¡õ
![$\Ht(\hat E)=\Ht([p])$](./latex/latex2png-MinorThesis2_222526200_-5.gif) . Since
. Since ![$[p]$](./latex/latex2png-MinorThesis2_2132972_-5.gif) has degree
has degree 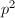 ,
, ![$\deg_i([p])$](./latex/latex2png-MinorThesis2_33765550_-5.gif) is either 1,
is either 1, 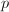 or
or 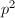 , therefore
, therefore ![$\Ht([p])$](./latex/latex2png-MinorThesis2_31096577_-5.gif) is either 0, 1, or 2. But
is either 0, 1, or 2. But ![$[p]'(T)\omega(T)=p\omega(T)=0$](./latex/latex2png-MinorThesis2_24850612_-5.gif) and
and 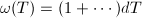 , where
, where  is the normalized invariant differential on
is the normalized invariant differential on 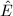 , hence we conclude that
, hence we conclude that ![$[p]'(T)=0$](./latex/latex2png-MinorThesis2_262296495_-5.gif) . It follows that
. It follows that ![$\Ht([p])\ge1$](./latex/latex2png-MinorThesis2_267481659_-5.gif) , so the possible height is either 1 or 2.
¡õ
, so the possible height is either 1 or 2.
¡õ
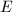 be an elliptic curve over
be an elliptic curve over  with
with 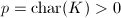 . Then
. Then
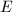 is supersingular if and only if
is supersingular if and only if  .
. if and only if
if and only if  and
and 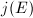 is transcendental over
is transcendental over 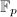 .
.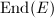 is an order in an imaginary quadratic extension of
is an order in an imaginary quadratic extension of 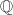 if and only if
if and only if  and
and 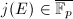 .
.
In particular, 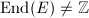 when
when 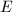 is defined over a finite field.
is defined over a finite field.
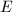 is supersingular if and only if
is supersingular if and only if ![$[p]$](./latex/latex2png-MinorThesis2_2132972_-5.gif) is purely inseparable, if and only if
is purely inseparable, if and only if ![$\deg_i[p]=p^2$](./latex/latex2png-MinorThesis2_9967981_-5.gif) . By Theorem 3, the last statement is true if and only if
. By Theorem 3, the last statement is true if and only if  .
.
For the remaining two parts, by Corollary 2, we know that  . Let us show that if
. Let us show that if  , then
, then 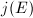 is transcendental over
is transcendental over 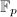 . Otherwise, suppose
. Otherwise, suppose 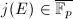 . We may assume
. We may assume 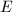 is defined over some finite field
is defined over some finite field 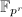 . Thus the Frobenius map
. Thus the Frobenius map 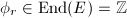 , and comparing degrees we obtain that
, and comparing degrees we obtain that ![$\phi_r=[\pm p^{r/2}]$](./latex/latex2png-MinorThesis2_7050730_-5.gif) . Hence
. Hence ![$[p]$](./latex/latex2png-MinorThesis2_2132972_-5.gif) is purely inseparable, a contradiction to
is purely inseparable, a contradiction to  by Theorem 3.
by Theorem 3.
Conversely, if 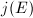 is transcendental, then
is transcendental, then 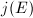 is a generic elliptic curve and every elliptic curve over
is a generic elliptic curve and every elliptic curve over  can be realized by specializing the value of
can be realized by specializing the value of 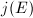 . By Theorem 1, every imaginary quadratic field in which
. By Theorem 1, every imaginary quadratic field in which 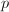 splits can occur as an endomorphism algebra and these endomorphism algebras have intersection
splits can occur as an endomorphism algebra and these endomorphism algebras have intersection 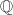 . Thus
. Thus  .
¡õ
.
¡õ
 Quaternion algebras
Quaternion algebras
We will do a quick summary of the basic properties of quaternion algebras in this section. See [3] for more proofs.
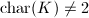 ,
, 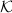 can be written as an algebra with basis
can be written as an algebra with basis 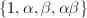 satisfying
satisfying 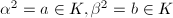 , and
, and 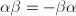 . We denote it by
. We denote it by 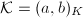 . Therefore this more general Definition 1 is compatible with the earlier Definition 5.
. Therefore this more general Definition 1 is compatible with the earlier Definition 5.
Let  be a global field,
be a global field,  be a place of
be a place of  , then there are only two isomorphism classes of quaternion algebras over the local field
, then there are only two isomorphism classes of quaternion algebras over the local field 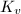 . One is the split case, i.e., the matrix algebra
. One is the split case, i.e., the matrix algebra 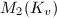 . Another is the ramified case, i.e., the unique division algebra
. Another is the ramified case, i.e., the unique division algebra 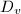 of dimension 4.
of dimension 4.
The quaternion algebra 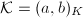 is ramified if and only if
is ramified if and only if 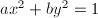 has no solution
has no solution 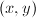 in
in  . By the Hasse-Minkowski Principle, the latter can be determined locally. Moreover, when
. By the Hasse-Minkowski Principle, the latter can be determined locally. Moreover, when 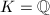 , we can use Hilbert symbol
, we can use Hilbert symbol 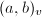 as a calculation tool to determine whether
as a calculation tool to determine whether 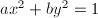 has a solution in
has a solution in 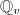 . Then the Hilbert reciprocity law
. Then the Hilbert reciprocity law 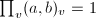 ensures that the number of places where
ensures that the number of places where 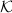 ramifies must be even.
ramifies must be even.
Two quaternion algebras are isomorphic if and only if they are isomorphic locally everywhere. Hence the places where 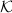 ramifies uniquely determine
ramifies uniquely determine 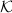 . Moreover, an order
. Moreover, an order 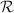 in
in 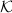 is maximal if and only if
is maximal if and only if 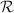 is maximal for all finite places.
is maximal for all finite places.
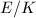 be a supersingular elliptic curve with
be a supersingular elliptic curve with 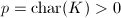 . Then
. Then 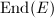 is an order in the unique rational quaternion algebra ramified only at
is an order in the unique rational quaternion algebra ramified only at 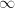 and
and 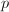 .
.
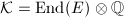 . By Definition 5 and Theorem 8, we know that
. By Definition 5 and Theorem 8, we know that 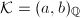 for some negative numbers
for some negative numbers  and
and 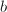 . Hence
. Hence 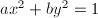 has no solution in
has no solution in 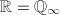 , which implies that
, which implies that 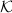 is ramified at
is ramified at 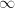 . For a prime
. For a prime 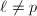 , we have an injection
, we have an injection  into
into 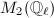 by Theorem 5 and Theorem 1. So
by Theorem 5 and Theorem 1. So  is isomorphic to
is isomorphic to 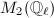 , namely
, namely 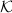 is split at all finite places away from
is split at all finite places away from 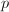 . But the total number of ramified places is even, hence we conclude that
. But the total number of ramified places is even, hence we conclude that 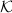 must ramify at
must ramify at 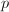 .
¡õ
.
¡õ
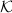 be a quaternion algebra over
be a quaternion algebra over 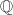 .
. 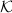 is called definite if
is called definite if 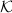 is ramified at
is ramified at  , otherwise
, otherwise 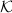 is called indefinite. Therefore Theorem 6 justifies this terminology in Definition 5.
is called indefinite. Therefore Theorem 6 justifies this terminology in Definition 5.
 Supersingular elliptic curves and maximal orders
Supersingular elliptic curves and maximal orders
Now we hope to show that the endomorphism ring of a supersingular elliptic curve over a finite field is actually a maximal order. It suffices to prove the maximality for all primes, that is, that 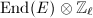 is a maximal order in
is a maximal order in  for all primes
for all primes 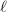 .
.
This could be hard. But it will be fairly easy if we quote the following two theorems. The first theorem is a special case of Tate's isogeny theorem about abelian varieties (see the next two sections). The second theorem is due to Dieudonné-Lubin ([4, Page 72]).
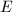 be an elliptic curve over a finite field
be an elliptic curve over a finite field  ,
, 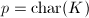 ,
, 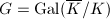 . Then for
. Then for 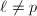 , there are isomorphisms
, there are isomorphisms 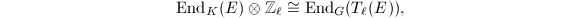 where the subscript
where the subscript 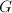 denotes the endomorphisms which commute with the
denotes the endomorphisms which commute with the 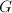 -action.
-action.
If 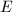 is in addition supersingular, then
is in addition supersingular, then 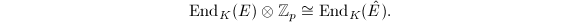
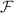 be a formal group of height
be a formal group of height 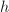 over a separably closed field
over a separably closed field  ,
, 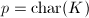 . Then
. Then 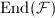 is a free
is a free 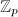 -module of rank
-module of rank 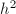 and is the maximal order in the local division algebra
and is the maximal order in the local division algebra 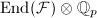 .
.
Using these two strong and useful results, we are now ready to prove the maximality of 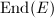 .
.
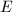 be a supersingular elliptic curve over a finite field with
be a supersingular elliptic curve over a finite field with 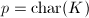 . Then
. Then 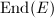 is a maximal order in the rational quaternion algebra ramified only at
is a maximal order in the rational quaternion algebra ramified only at 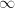 and
and 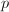 .
.
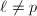 . Since
. Since 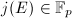 by Theorem 2,
by Theorem 2, 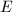 can be actually defined over
can be actually defined over  . So
. So 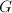 is generated by the
is generated by the 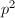 -th Frobenius map
-th Frobenius map 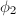 . Since
. Since 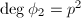 , we know that
, we know that ![$\psi\circ[p]=\phi_2$](./latex/latex2png-MinorThesis2_150075158_-5.gif) where
where 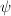 is an isomorphism ([2, II 2.12]). But the automorphism group of an elliptic curve has finite order ([2, III 10.1]), hence after passing to a finite extension
is an isomorphism ([2, II 2.12]). But the automorphism group of an elliptic curve has finite order ([2, III 10.1]), hence after passing to a finite extension 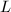 of
of  ,
, 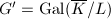 acts as scalars on
acts as scalars on 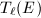 . So
. So 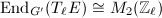 . By Theorem 6, we know
. By Theorem 6, we know 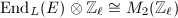 which is a maximal order in
which is a maximal order in 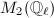 . But every endomorphism of
. But every endomorphism of 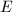 is defined over some finite field, so
is defined over some finite field, so 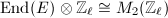 is a maximal order in
is a maximal order in 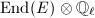 .
.
Since  is separably closed, using Theorem 7 we know that
is separably closed, using Theorem 7 we know that 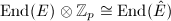 is isomorphic to the maximal order in the local quaternion algebra. The theorem follows.
¡õ
is isomorphic to the maximal order in the local quaternion algebra. The theorem follows.
¡õ
 Abelian varieties and Tate conjecture
Abelian varieties and Tate conjecture
Abelian varieties can be viewed as a higher dimensional generalization of elliptic curves. In this section we introduce some basic notions about abelian varieties and state the Tate conjecture and list the results about it. The main references for this and the next sections are [5] and [6].
An abelian variety over  is a complete connected group variety over
is a complete connected group variety over  , or equivalently, a projective connected group variety over
, or equivalently, a projective connected group variety over  ([5, I 6.4]). As we expected, its group structure is automatically commutative ([5, I 1.4]).
([5, I 6.4]). As we expected, its group structure is automatically commutative ([5, I 1.4]).
Analogously to elliptic curves, an isogeny between two abelian varieties is an homomorphism of abelian varieties which is surjective and has finite kernel. An abelian variety is called simple if it does not contain any nontrivial abelian variety. Every abelian variety is isogenous to a product of simple abelian varieties ([5, I 10.1]).
The multiplication-by-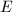 map is an isogeny of degree
map is an isogeny of degree 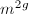 , where
, where 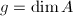 . Moreover, it is an étale map if
. Moreover, it is an étale map if 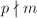 , where
, where 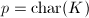 ([5, I 7.2]). Similarly, for a prime
([5, I 7.2]). Similarly, for a prime 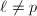 , the
, the 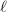 -adic Tate module
-adic Tate module 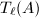 of an abelian variety
of an abelian variety 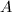 over
over  is the inverse limit of the
is the inverse limit of the 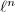 -torsion part (over
-torsion part (over  ) of
) of 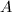 ; it is a
; it is a 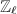 -module along with a
-module along with a 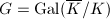 -action. So
-action. So 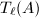 is a free
is a free 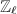 -module of rank
-module of rank 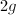 ([6, 19]). For any two abelian varieties
([6, 19]). For any two abelian varieties 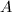 and
and 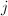 , we have a natural homomorphism of
, we have a natural homomorphism of 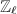 -modules
-modules
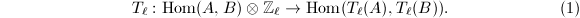 The injectivity of Theorem 5 also holds for abelian varieties using similar argument ([5, I 10.5]).
The injectivity of Theorem 5 also holds for abelian varieties using similar argument ([5, I 10.5]).
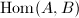 is a free
is a free 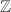 -module of rank at most
-module of rank at most 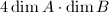 .
.
The next corollary follows easily from Theorem 9.
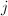 is a simple abelian variety, then every endomorphism
is a simple abelian variety, then every endomorphism 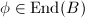 is automatically an isogeny, hence
is automatically an isogeny, hence 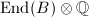 is a division algebra
is a division algebra 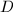 . Therefore the endomorphism algebra of any abelian variety
. Therefore the endomorphism algebra of any abelian variety 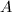 is a product of matrix algebras
is a product of matrix algebras 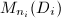 . Now, by Theorem 9, the
. Now, by Theorem 9, the 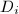 's are finite dimensional, hence
's are finite dimensional, hence 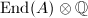 is semisimple by the Artin-Wedderburn theorem.
¡õ
is semisimple by the Artin-Wedderburn theorem.
¡õ
Taking 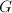 -invariants on both sides of (1) we get an injective homomorphism
-invariants on both sides of (1) we get an injective homomorphism
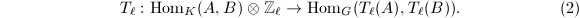 Tate [7] conjectured that in many cases it is also an isomorphism.
Tate [7] conjectured that in many cases it is also an isomorphism.
 is finitely generated over its prime field (e.g. finite fields, number fields or global function fields).
is finitely generated over its prime field (e.g. finite fields, number fields or global function fields).
This conjecture for finite fields was proved by Tate himself [8], now called Tate's isogeny theorem. Zarhin [9] proved the Tate conjecture for function fields of positive characteristic. The number field case was proved by Faltings [10] as one of the steps in proving the Mordell conjecture. Faltings [11] proved the case for function fields of characteristic zero.
There is also a 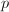 -analog of the
-analog of the 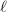 -adic Tate module
-adic Tate module 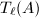 called the Dieudonné module
called the Dieudonné module 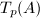 , constructed from the
, constructed from the 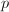 -divisible group
-divisible group ![$A[p^{\infty}]$](./latex/latex2png-MinorThesis2_186090436_-5.gif) . Tate conjectured that
. Tate conjectured that
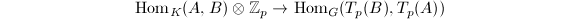 is an isomorphism if
is an isomorphism if  is finitely generated over its prime field (e.g., finite fields, number fields or global function fields).
is finitely generated over its prime field (e.g., finite fields, number fields or global function fields).
This conjecture was proved for finite fields by Tate himself (see [14]), and for function fields over finite fields by de Jong [15]. Under certain conditions, there is an equivalence of categories between 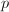 -divisible groups and formal groups [16]. In particular, when
-divisible groups and formal groups [16]. In particular, when 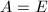 is a supersingular elliptic curve (hence without
is a supersingular elliptic curve (hence without 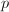 -torsion), the
-torsion), the 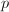 -divisible group can be identified with the formal group
-divisible group can be identified with the formal group 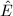 .
.
 Finiteness theorem and Tate's isogeny theorem
Finiteness theorem and Tate's isogeny theorem
In this section, we will discuss some basic properties of abelian varieties. We will sketch the main steps of the proof of Tate's isogeny theorem. Before doing that, we will first prove a finiteness theorem on abelian varieties over a finite field, which turns out to be one of the key steps in the proof.
Let 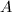 be an abelian variety and
be an abelian variety and 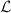 be a line bundle on
be a line bundle on 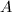 , then the theorem of square ([5, I 5.5]) ensures that
, then the theorem of square ([5, I 5.5]) ensures that  is a homomorphism where
is a homomorphism where 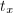 is the translation-by-
is the translation-by- isogeny. Let
isogeny. Let  be the isomorphism classes of all line bundles
be the isomorphism classes of all line bundles  satisfying
satisfying 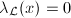 for any
for any 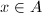 . When
. When 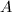 is an elliptic curve and
is an elliptic curve and 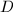 is a divisor on
is a divisor on 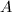 , then
, then 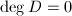 if and only if
if and only if 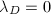 , so this definition is compatible with the earlier
, so this definition is compatible with the earlier 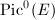 . One can show
. One can show 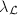 actually maps onto
actually maps onto  ([6, 8]).
([6, 8]).
There is a pair consisting of a dual abelian variety and a Poincaré bundle 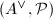 which is the solution to the moduli problem of parametrizing
which is the solution to the moduli problem of parametrizing  ([6, 13]). A polarization of
([6, 13]). A polarization of 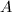 is an isogeny
is an isogeny 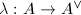 such that
such that 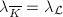 for some ample line bundle
for some ample line bundle  on
on 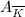 . If
. If 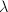 has degree one, then
has degree one, then 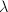 is called a principal polarization.
is called a principal polarization.
There are several interesting results about line bundles on abelian varieties.
Over a finite field, there are only finitely many isomorphism classes of elliptic curves since there are only finitely many 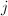 -invariants. This finiteness result can be extended to abelian varieties ([5, I 11.2]).
-invariants. This finiteness result can be extended to abelian varieties ([5, I 11.2]).
 be a finite field and
be a finite field and 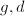 be two fixed positive integers. Then up to isomorphism, there are only finitely many abelian varieties over
be two fixed positive integers. Then up to isomorphism, there are only finitely many abelian varieties over  of dimension
of dimension  possessing a polarization of degree
possessing a polarization of degree 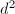 .
.
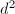 can be realized as a subvariety of degree
can be realized as a subvariety of degree 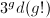 in a
in a 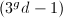 dimensional projective space, in other words, a rational point on the corresponding Chow variety. But
dimensional projective space, in other words, a rational point on the corresponding Chow variety. But  is a finite field, so there are only finite many rational points on this Chow variety. The result follows.
¡õ
is a finite field, so there are only finite many rational points on this Chow variety. The result follows.
¡õ
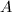 be an abelian variety over a number field
be an abelian variety over a number field  , then up to isomorphism there are only finitely many abelian varieties over
, then up to isomorphism there are only finitely many abelian varieties over  which are isogenous to
which are isogenous to 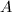 .
.
Let us sketch the major steps of the proof of Tate's isogeny theorem to end this chapter.
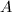 be an abelian variety over a finite field
be an abelian variety over a finite field  ,
, 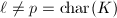 be a prime,
be a prime, 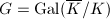 . Then the natural map
. Then the natural map 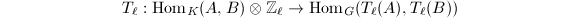 is an isomorphism.
is an isomorphism.
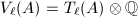 . Reduce to showing that the natural map
. Reduce to showing that the natural map  is an isomorphism. Since this is an injection and the dimension of
is an isomorphism. Since this is an injection and the dimension of 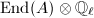 is independent of
is independent of 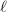 , it suffices to show that it is an isomorphism for one
, it suffices to show that it is an isomorphism for one 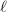 and that all
and that all 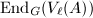 's have the same dimension.
's have the same dimension.
Step 2 Let 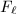 be the subalgebra of
be the subalgebra of 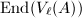 generated by the automorphisms of
generated by the automorphisms of 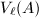 defined by elements of
defined by elements of 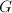 . To prove the isomorphism, it is equivalent to show that
. To prove the isomorphism, it is equivalent to show that 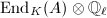 is the commutant of
is the commutant of 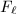 in
in 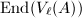 . Since
. Since 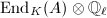 is semisimple, it suffices to show that
is semisimple, it suffices to show that 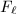 is the commutant of
is the commutant of 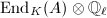 in
in 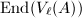 by the von Neumann bicommutant theorem.
by the von Neumann bicommutant theorem.
Step 3 Let 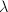 be a polarization of
be a polarization of 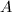 . Define a pairing
. Define a pairing  on
on 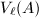 by setting
by setting 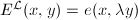 where
where  is the pairing of
is the pairing of 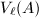 and
and 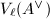 induced by the Weil pairing. Let
induced by the Weil pairing. Let  be a subspace of
be a subspace of 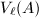 which is maximally isotropic with respect to the pairing
which is maximally isotropic with respect to the pairing  and stable under
and stable under 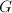 -action. Use the Finiteness Theorem 11 to construct an endomorphism
-action. Use the Finiteness Theorem 11 to construct an endomorphism 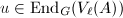 such that
such that 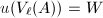 .
.
Step 4 Let 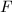 be the subalgebra of
be the subalgebra of 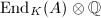 generated by the Frobenius endomorphisms of
generated by the Frobenius endomorphisms of 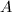 over
over  . Show that for any
. Show that for any 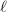 which splits completely in
which splits completely in 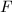 , we have
, we have 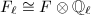 and use Step 3 to show that
and use Step 3 to show that 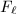 is the commutant of
is the commutant of 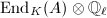 in
in 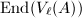 .
.
Step 5 Use the semisimplicity of the Frobenius map on 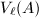 to show that all
to show that all 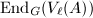 's have the same dimension and complete the proof by Step 1.
¡õ
's have the same dimension and complete the proof by Step 1.
¡õ
References
[1]Die typen der multiplikatorenringe elliptischer funktionenkörper, Abhandlungen aus dem mathematischen Seminar der Universität Hamburg, 14 1941, 197--272.
[2]The Arithmetic of Elliptic Curves, Springer, 2010.
[3]Introduction To Quadratic Forms Over Fields, Amer Mathematical Society, 2004.
[4]Formal groups, Springer-Verlag, Berlin, New York, 1968.
[5]Abelian Varieties, 2008, http://www.jmilne.org/math/CourseNotes/AV.pdf.
[6]Abelian Varieties, Oxford University, 1970.
[7]Arithmetical Algebraic Geometry, Algebraic Cycles and Poles of Zeta Functions, Harper and Row, 1965.
[8]Endomorphisms of abelian varieties over finite fields, Inventiones mathematicae 2 (1966), no.2, 134--144.
[9]Endomorphisms of Abelian varieties over fields of finite characteristic, Mathematics of the USSR-Izvestiya 9 (1975), 255.
[10]Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Inventiones mathematicae 73 (1983), no.3, 349--366.
[11]Rational Points, Friedrich Vieweg \& Sohn Verlag, 1992.
[12]Abelian varieties over finite fields, Higher-Dimensional Geometry over Finite Fields, IOS Press, 2008.
[13]Abelian varieties over finite fields, Ann. Sci. Ecole Norm. Sup 4 (1969), no.2, 521--560.
[14]Abelian varieties over finite fields, 1969 Number Theory Institute 4 (1971), 53 -- 64.
[15]Homomorphisms of Barsotti-Tate groups and crystals in positive characteristic, Inventiones Mathematicae 134 (1998), no.2, 301--333.
[16]p-Divisible groups, Proc Conf. Local Fields, Driebergen, 1966, 158--183.
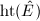 is either 1 or 2.
is either 1 or 2.
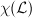 . Then
. Then
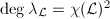 . If
. If 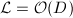 , then
, then 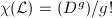 where
where 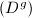 is the
is the  is very ample for every
is very ample for every 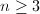 (
(