Our main goal in this chapter is to characterize the endomorphism rings of elliptic curves. Surprisingly, it turns out that there are only three possibilities: the ring of integers 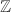 , an order in an imaginary quadratic extension of
, an order in an imaginary quadratic extension of 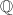 , or an order in a quaternion algebra over
, or an order in a quaternion algebra over 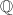 . Among others, the dual isogeny and the Tate module play key roles in the proof. We will recall the basic notions of elliptic curves in the first section by looking at their various equivalent definitions. Before proving the general case, we will also illustrate the special case of
. Among others, the dual isogeny and the Tate module play key roles in the proof. We will recall the basic notions of elliptic curves in the first section by looking at their various equivalent definitions. Before proving the general case, we will also illustrate the special case of 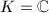 as an example, in an attempt to get a clue as to the general proof. The main source of our exposition is [1].
as an example, in an attempt to get a clue as to the general proof. The main source of our exposition is [1].
 Elliptic curves
Elliptic curves
Let us get started by recalling some basic notions about elliptic curves. The rich structure of an elliptic curve allows us to define it in various flavors. We may summarize them as follows.
 over a field
over a field 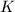 is
is
- an irreducible smooth projective curve over
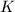 of genus one
with a specified point
of genus one
with a specified point 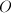 , or
, or - a plane projective curve defined by a Weierstrass equation
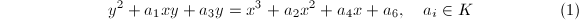 with nonzero discriminant. For
with nonzero discriminant. For 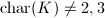 , the Weierstrass
equation can be simplified via a change of variables to
, the Weierstrass
equation can be simplified via a change of variables to
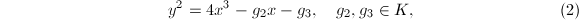 or
or - (
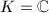 ) a one-dimensional complex torus,
i.e.
) a one-dimensional complex torus,
i.e. 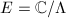 for some lattice
for some lattice 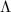 in
in
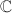 , or
, or - a one-dimensional abelian variety over
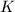 , i.e., a connected
projective curve over
, i.e., a connected
projective curve over 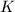 with a group structure.
with a group structure.
Let us now elaborate on some of the connections between these definitions.
(a)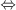 (b) Suppose
(b) Suppose  satisfies (a). By the Riemann-Roch theorem, for any
satisfies (a). By the Riemann-Roch theorem, for any 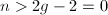 , we have
, we have 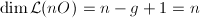 . Letting
. Letting 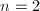 and
and 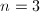 , we can find two functions
, we can find two functions 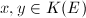 such that
such that  has exactly 2 poles at
has exactly 2 poles at 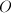 and
and 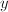 has exactly 3 poles at
has exactly 3 poles at 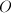 . Now let
. Now let  , we get a linear relation between
, we get a linear relation between 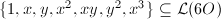 which gives us the Weierstrass equation (1). The map
which gives us the Weierstrass equation (1). The map ![$$\phi: E\rightarrow \mathbb{P}^2,\qquad \phi=[x,y,1]$$](./latex/latex2png-MinorThesis1_74823194_.gif) sends
sends  onto a plane projective curve defined by a Weierstrass equation. The extension degrees
onto a plane projective curve defined by a Weierstrass equation. The extension degrees ![$[K(E):K(x)]=2$](./latex/latex2png-MinorThesis1_226583684_-5.gif) and
and ![$[K(E):K(y)]=3$](./latex/latex2png-MinorThesis1_226649221_-5.gif) implies that
implies that ![$[K(E):K(x,y)]=1$](./latex/latex2png-MinorThesis1_234088194_-5.gif) , hence
, hence  has degree 1 and gives an isomorphism between
has degree 1 and gives an isomorphism between  and
and 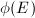 . Since
. Since  is smooth, we know that the discriminant of the Weierstrass equation is nonzero. Moreover,
is smooth, we know that the discriminant of the Weierstrass equation is nonzero. Moreover, ![$\phi(O)=[0,1,0]$](./latex/latex2png-MinorThesis1_58768635_-5.gif) is the point at infinity.
is the point at infinity.
Conversely, suppose  is a plane projective curve defined by a Weierstrass equation. The fact that the discriminant is nonzero means that
is a plane projective curve defined by a Weierstrass equation. The fact that the discriminant is nonzero means that  is smooth. To see that
is smooth. To see that  has genus 1, consider the invariant differential
has genus 1, consider the invariant differential 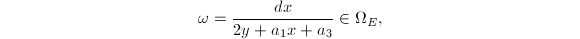 It is holomorphic and non-vanishing, hence
It is holomorphic and non-vanishing, hence 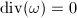 . By the Riemann-Roch theorem,
. By the Riemann-Roch theorem, 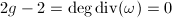 , which implies that
, which implies that 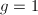 . Finally, the specified point is taken to be the point at infinity.
. Finally, the specified point is taken to be the point at infinity.
(b) (c) Suppose
(c) Suppose  satisfies (c),
satisfies (c), 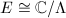 . Define
. Define ![$$\phi:\mathbb{C}/\Lambda\rightarrow \mathbb{P}^2,\qquad z\mapsto [\wp_\Lambda(z),\wp_\Lambda'(z),1]$$](./latex/latex2png-MinorThesis1_200370993_.gif) where the Weierstrass
where the Weierstrass 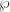 -function is given by
-function is given by 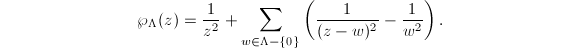 Then
Then 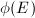 is the plane projective curve cut out by (2) with
is the plane projective curve cut out by (2) with 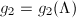 and
and 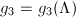 where
where 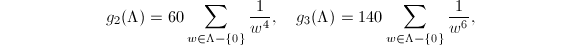 are Eisenstein series of weights 4 and 6. Let
are Eisenstein series of weights 4 and 6. Let 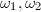 be a basis of the lattice
be a basis of the lattice 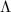 and
and 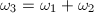 . Then the equation (2) has three distinct roots
. Then the equation (2) has three distinct roots 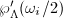 , so the discriminant is nonzero. One can show that
, so the discriminant is nonzero. One can show that 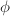 is injective using the properties of elliptic functions ([1, VI 3.6]). Since
is injective using the properties of elliptic functions ([1, VI 3.6]). Since 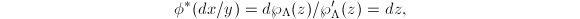 we know that
we know that 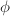 induces an isomorphism on the cotangent spaces. Thus
induces an isomorphism on the cotangent spaces. Thus 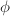 is an isomorphism between
is an isomorphism between  and
and 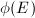 .
.
Conversely, for any 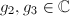 such that the discriminant is nonzero, there exists a unique lattice
such that the discriminant is nonzero, there exists a unique lattice 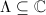 satisfying
satisfying 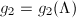 and
and 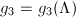 by the Uniformization theorem ([2, I 4.3]). Thus the plane projective curve
by the Uniformization theorem ([2, I 4.3]). Thus the plane projective curve  is isomorphic to the complex torus
is isomorphic to the complex torus 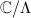 .
.
(a)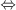 (c) Suppose
(c) Suppose  satisfies (a). Then
satisfies (a). Then  is a genus one Riemann surface. Let
is a genus one Riemann surface. Let 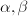 be the fundamental loops of
be the fundamental loops of  generating
generating 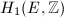 and let
and let 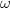 be the canonical differential on
be the canonical differential on  , then
, then 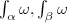 are
are 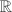 -linearly independent. Let
-linearly independent. Let 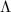 be the lattice spanned by them. The Abel-Jacobi map
be the lattice spanned by them. The Abel-Jacobi map 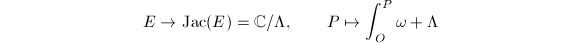 is biholomorphic by the Jacobi inversion theorem ([3, Theorem 5.1]).
is biholomorphic by the Jacobi inversion theorem ([3, Theorem 5.1]).
Conversely, the one-dimensional complex torus  is of genus 1. The specified point is taken to be
is of genus 1. The specified point is taken to be 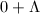 .
.
(a) (d) Suppose
(d) Suppose  satisfies (a). For any two points
satisfies (a). For any two points 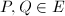 ,
, 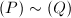 if and only if
if and only if 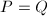 , since
, since 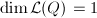 by the Riemann-Roch theorem and
by the Riemann-Roch theorem and 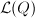 contains constant functions. Therefore we have an injective map from
contains constant functions. Therefore we have an injective map from  to its degree-0 Picard group
to its degree-0 Picard group  Again, by the Riemann-Roch theorem,
Again, by the Riemann-Roch theorem, 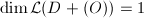 for any degree-0 divisor
for any degree-0 divisor 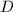 . Let
. Let 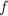 be a basis vector of this one-dimensional space. Then
be a basis vector of this one-dimensional space. Then 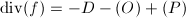 for some
for some  , so we get
, so we get 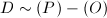 and thus
and thus 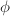 is also surjective. So
is also surjective. So  has a group structure inherited from
has a group structure inherited from 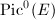 and
and 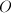 serves as the identity element. Moreover,
serves as the identity element. Moreover,  is irreducible, so connected.
is irreducible, so connected.
Conversely, suppose  has a group structure. Then by generic smoothness we know
has a group structure. Then by generic smoothness we know  is smooth.
is smooth.  is connected and smooth, hence irreducible. Moreover, the canonical bundle
is connected and smooth, hence irreducible. Moreover, the canonical bundle 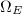 is free of rank 1 and has degree
is free of rank 1 and has degree 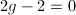 , therefore the genus
, therefore the genus 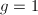 .
.
(b) (d) The group structure on
(d) The group structure on  can be written down in terms of secants and tangents given by regular functions of the coordinates
can be written down in terms of secants and tangents given by regular functions of the coordinates 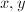 with coefficients
with coefficients 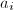 . The point at infinity serves as the identity element.
. The point at infinity serves as the identity element.
(c)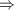 (d) The group structure on
(d) The group structure on  is given by
is given by 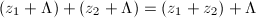 . The point
. The point 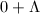 serves as the identity element. The properties of elliptic functions also ensure a bijection between
serves as the identity element. The properties of elliptic functions also ensure a bijection between 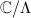 and
and 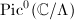 ([1, VI 2.4]). These two group structures are compatible with each other.
([1, VI 2.4]). These two group structures are compatible with each other.
 Isogeny and dual isogeny
Isogeny and dual isogeny
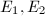 be two elliptic curves. An isogeny from
be two elliptic curves. An isogeny from 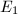 to
to 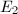 is a morphism
is a morphism 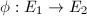 satisfying
satisfying 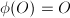 . The group of isogenies from
. The group of isogenies from 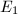 to
to 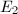 is denoted by
is denoted by 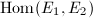 . The ring of endomorphisms of an elliptic curve
. The ring of endomorphisms of an elliptic curve  , i.e., the isogenies from
, i.e., the isogenies from  to itself, is denoted by
to itself, is denoted by 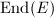 . For those isogenies defined over
. For those isogenies defined over 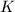 , we denote them by
, we denote them by 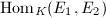 and
and 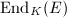 respectively.
respectively.
An isogeny is automatically a homomorphism. An isogeny 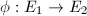 is the same as the composition
is the same as the composition 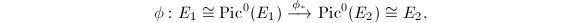 where
where 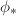 is the pushforward map between Picard groups induced by the isogeny
is the pushforward map between Picard groups induced by the isogeny 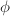 . All these three maps are group homomorphisms, hence the composition
. All these three maps are group homomorphisms, hence the composition 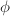 itself is a group homomorphism.
itself is a group homomorphism.
One can also consider the pullback map 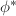 of Picard groups induced by
of Picard groups induced by 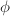 , the composition
, the composition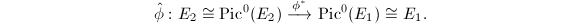 turns out to be an isogeny from
turns out to be an isogeny from 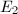 to
to 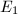 as well and the composition
as well and the composition 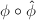 has the effect
has the effect ![$\phi_*\circ\phi^*=[\deg\phi]$](./latex/latex2png-MinorThesis1_237544963_-5.gif) .
.
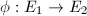 be an isogeny of elliptic curves of degree
be an isogeny of elliptic curves of degree 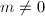 , then there exists a unique isogeny
, then there exists a unique isogeny 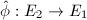 such that
such that ![$\hat\phi\circ\phi=[m]$](./latex/latex2png-MinorThesis1_61949799_-5.gif) , where
, where ![$[m]$](./latex/latex2png-MinorThesis1_5278700_-5.gif) denotes the multiplication-by-
denotes the multiplication-by- isogeny.
isogeny. 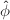 is called the dual isogeny to
is called the dual isogeny to 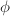 .
.
Here we list some easy properties of the dual isogeny as follows ([1, III 6.2]).
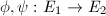 ,
, 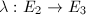 be isogenies of elliptic curves.
be isogenies of elliptic curves.
- Let
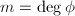 , then
, then ![$\hat\phi\circ\phi=[m]$](./latex/latex2png-MinorThesis1_61949799_-5.gif) on
on 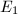 and
and ![$\phi\circ\hat\phi=[m]$](./latex/latex2png-MinorThesis1_134121256_-5.gif) on
on 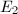 . In particular,
. In particular, 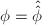 .
. 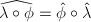 .
.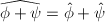 .
.![$\widehat{[m]}=[m]$](./latex/latex2png-MinorThesis1_261512132_-5.gif) and
and ![$\deg[m]=m^2$](./latex/latex2png-MinorThesis1_82459707_-5.gif) for any
for any 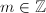 .
.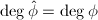 .
.
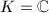 . In this case we can write down the isogenies, dual isogenies and endomorphism rings in very concrete terms.
. In this case we can write down the isogenies, dual isogenies and endomorphism rings in very concrete terms.
Isogeny Suppose 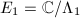 and
and 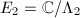 are two elliptic curves and
are two elliptic curves and 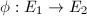 is an isogeny. Then, by the lifting property of the covering space, the holomorphic map
is an isogeny. Then, by the lifting property of the covering space, the holomorphic map 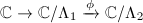 can be lifted to a holomorphic map
can be lifted to a holomorphic map 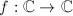 , since the source
, since the source 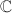 is simply-connected. For any
is simply-connected. For any 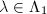 ,
, 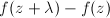 maps into a discrete subset of
maps into a discrete subset of 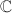 , hence must be constant. Therefore,
, hence must be constant. Therefore, 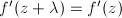 ; in other words,
; in other words, 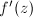 is an elliptic function with respect to the lattice
is an elliptic function with respect to the lattice 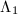 . But
. But 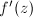 is also holomorphic, hence
is also holomorphic, hence 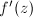 must be a constant and
must be a constant and 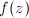 is a linear map. Now
is a linear map. Now 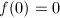 implies that
implies that 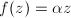 for some
for some 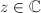 . In summary,
. In summary, 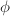 must be of the form
must be of the form 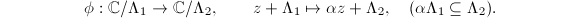 There is a bijection
There is a bijection 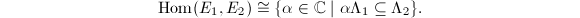
Dual isogeny Suppose 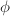 corresponds to
corresponds to 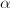 in the manner mentioned above. Then
in the manner mentioned above. Then 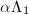 is a sublattice of
is a sublattice of 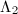 . Let
. Let 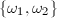 be a basis of
be a basis of 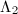 , then we can find two integers
, then we can find two integers 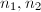 such that
such that 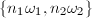 forms a basis of
forms a basis of 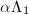 . Moreover,
. Moreover, 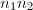 is exactly the degree of
is exactly the degree of 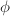 . Now
. Now 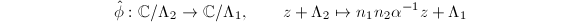 is a well-defined isogeny since
is a well-defined isogeny since 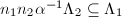 . Also, it is easy to see that
. Also, it is easy to see that ![$$\hat\phi\circ\phi=[n_1n_2]=[\deg\phi],$$](./latex/latex2png-MinorThesis1_70992461_.gif) namely
namely 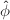 is just the dual isogeny of
is just the dual isogeny of 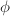 .
.
Endomorphism ring From the above discussion, we know that 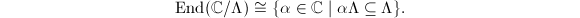 Suppose
Suppose 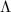 has a basis
has a basis 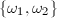 . Without loss of generality, we may multiply
. Without loss of generality, we may multiply 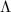 by
by 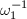 and assume that
and assume that 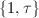 is a basis of
is a basis of 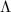 where
where 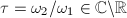 . Let
. Let 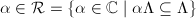 , then we can find integers
, then we can find integers 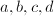 such that
such that 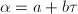 and
and 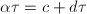 . So
. So 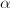 satisfies a quadratic equation
satisfies a quadratic equation 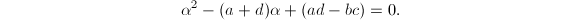 Hence
Hence 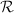 is an integral extension of
is an integral extension of 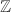 . Now suppose
. Now suppose 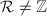 , then we can find some
, then we can find some 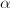 with
with 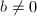 . Eliminating
. Eliminating 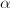 yields another quadratic equation in
yields another quadratic equation in  ,
, 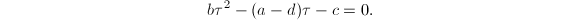 So
So 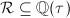 is an order in an imaginary quadratic extension of
is an order in an imaginary quadratic extension of 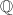 . In summary,
. In summary, 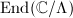 can be either
can be either 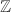 consisting of multiplication-by-
consisting of multiplication-by- maps, or an order in an imaginary quadratic field
maps, or an order in an imaginary quadratic field 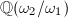 .
.
Elliptic curves in the latter case, which are relatively rare compared to the first case, are said to have complex multiplication, or CM for short. We will see more interesting examples and properties of elliptic curves with complex multiplication later in the third chapter.
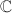 , we are able to conclude that over an arbitrary field of characteristic 0, the endomorphism ring
, we are able to conclude that over an arbitrary field of characteristic 0, the endomorphism ring 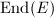 only has the above two classes as well. However, some interesting phenomena happen in positive characteristic. An extra class, called supersingular elliptic curves, with endomorphism ring an order in a rational quaternion algebra, can appear.
only has the above two classes as well. However, some interesting phenomena happen in positive characteristic. An extra class, called supersingular elliptic curves, with endomorphism ring an order in a rational quaternion algebra, can appear.
 The Tate module
The Tate module
As we saw, the endomorphisms of elliptic curves over 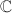 can be described as endomorphisms of the lattice
can be described as endomorphisms of the lattice 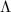 , which is a rank 2 free
, which is a rank 2 free 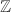 -module. But in the general case, there is no possible way to assign a rank 2 free
-module. But in the general case, there is no possible way to assign a rank 2 free 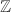 -module functorially, since a rational quaternion algebra has no two-dimensional
-module functorially, since a rational quaternion algebra has no two-dimensional 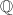 -representation and therefore
-representation and therefore 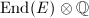 cannot act on
cannot act on 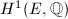 for supersingular elliptic curves. However, we can assign a rank 2 free
for supersingular elliptic curves. However, we can assign a rank 2 free 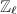 -module (Corollary 1) functorially for
-module (Corollary 1) functorially for 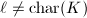 , namely the
, namely the 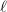 -adic Tate module
-adic Tate module 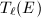 .
.
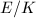 be an elliptic curve and
be an elliptic curve and ![$E[m]=\ker[m]$](./latex/latex2png-MinorThesis1_257991852_-5.gif) be the
be the  -torsion part of
-torsion part of  (over
(over 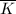 ). Let
). Let 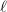 be a prime. The
be a prime. The 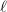 -adic Tate module
-adic Tate module 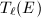 is defined to be the inverse limit
is defined to be the inverse limit ![$\varprojlim E[\ell^n]$](./latex/latex2png-MinorThesis1_134778316_-10.gif) with respect to the multiplication-by-
with respect to the multiplication-by-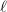 maps
maps ![$[\ell]$](./latex/latex2png-MinorThesis1_123757022_-5.gif) .
.
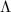 as the first cohomology group
as the first cohomology group 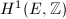 and the
and the  -torsion part
-torsion part ![$E[m]\cong m^{-1}\Lambda/\Lambda\cong \mathbb{Z}/m\mathbb{Z}\times\mathbb{Z}/m\mathbb{Z}$](./latex/latex2png-MinorThesis1_170479474_-5.gif) as the first cohomology group
as the first cohomology group 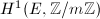 . Analogously, in the positive characteristic case, we may interpret
. Analogously, in the positive characteristic case, we may interpret 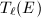 as the first étale cohomology group
as the first étale cohomology group 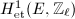 and
and ![$E[m]$](./latex/latex2png-MinorThesis1_263156794_-5.gif) as the first étale cohomology group
as the first étale cohomology group 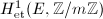 .
.
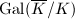 acts naturally on
acts naturally on ![$E[\ell^n]$](./latex/latex2png-MinorThesis1_88769578_-5.gif) and the action commutes with
and the action commutes with ![$[\ell]$](./latex/latex2png-MinorThesis1_123757022_-5.gif) , it produces a continuous
, it produces a continuous 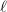 -adic Galois representation
-adic Galois representation 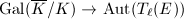 .
.
For fields of positive characteristic, the 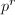 -torsion part can ``collapse'' somewhat since the isogeny
-torsion part can ``collapse'' somewhat since the isogeny ![$[p^r]$](./latex/latex2png-MinorThesis1_50296497_-5.gif) is not separable ([1, III 6.4]).
is not separable ([1, III 6.4]).
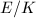 be an elliptic curve. Then
be an elliptic curve. Then
![$E[m]\cong\prod_q E[q^{r_q}]$](./latex/latex2png-MinorThesis1_57115316_-8.gif) , where
, where  is a positive integer with prime factorization
is a positive integer with prime factorization 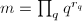 .
.- If
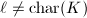 , then
, then ![$E[\ell^r]\cong\mathbb{Z}/\ell^r\mathbb{Z}\times\mathbb{Z}/\ell^r\mathbb{Z}$](./latex/latex2png-MinorThesis1_211568906_-5.gif) .
. - If
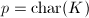 , then either
, then either ![$E[p^r]\cong 0$](./latex/latex2png-MinorThesis1_10312040_-5.gif) for any
for any 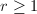 or
or ![$E[p^e]\cong \mathbb{Z}/p^r\mathbb{Z}$](./latex/latex2png-MinorThesis1_252606314_-5.gif) for any
for any 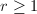 .
.
From Theorem 2, the next corollary about the structure of the Tate modules follows immediately.
 Classification of endomorphism rings
Classification of endomorphism rings
In this section, we will classify the endomorphism rings of elliptic curves over an arbitrary field. Let us start by making several simple observations.
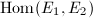 is a torsion-free
is a torsion-free 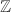 -module.
-module. 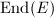 is a (not necessarily commutative) ring of characteristic 0 and has no zero divisors.
is a (not necessarily commutative) ring of characteristic 0 and has no zero divisors.
 be an integer. Suppose
be an integer. Suppose 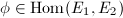 satisfies
satisfies ![$[m]\circ\phi=0$](./latex/latex2png-MinorThesis1_185041127_-5.gif) . Taking degrees gives
. Taking degrees gives ![$(\deg[m])(\deg\phi)=0$](./latex/latex2png-MinorThesis1_48709056_-5.gif) . If
. If 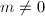 , then
, then ![$[m]$](./latex/latex2png-MinorThesis1_5278700_-5.gif) is a non-constant isogeny ([1, III 4.2 (a)]),
is a non-constant isogeny ([1, III 4.2 (a)]), ![$\deg[m]\ne0$](./latex/latex2png-MinorThesis1_168018887_-5.gif) . Thus
. Thus 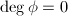 and
and 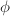 itself is
itself is ![$[0]$](./latex/latex2png-MinorThesis1_27298796_-5.gif) .
.
In particular, 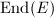 is a ring of characteristic 0. If
is a ring of characteristic 0. If 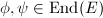 satisfy
satisfy 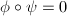 , similarly taking degrees will give
, similarly taking degrees will give 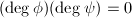 , which implies
, which implies ![$\phi=[0]$](./latex/latex2png-MinorThesis1_243892311_-5.gif) or
or ![$\psi=[0]$](./latex/latex2png-MinorThesis1_243892487_-5.gif) . So
. So 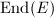 has no zero divisors.
¡õ
has no zero divisors.
¡õ
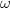 be an invariant differential on
be an invariant differential on  . For any
. For any 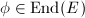 , there exists a rational function
, there exists a rational function 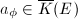 such that
such that 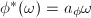 since
since 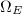 is a one-dimensional
is a one-dimensional 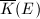 -vector space. But
-vector space. But 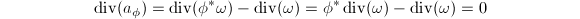 since
since 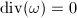 . So
. So 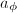 is a constant in
is a constant in 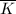 . Now, we have a map
. Now, we have a map 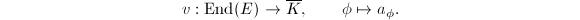 Then
Then  is a ring homomorphism because
is a ring homomorphism because 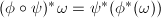 and
and 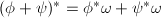 ([1, III 5.2]). By assumption
([1, III 5.2]). By assumption 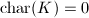 , so any nonconstant isogeny
, so any nonconstant isogeny 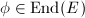 is a separable morphism. Thus
is a separable morphism. Thus 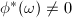 and then
and then 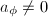 . We conclude that
. We conclude that  is an injection. Because
is an injection. Because 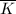 is commutative, it follows that
is commutative, it follows that 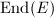 is commutative. %
¡õ
is commutative. %
¡õ
For an isogeny 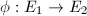 ,
, 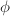 induces a homomorphism on the
induces a homomorphism on the 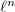 -torsion parts, hence a
-torsion parts, hence a 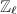 -module homomorphism of the Tate modules. The next theorem allows us to extract information from the Tate modules to get information about the isogenies. We will see more of this idea in the next chapter.
-module homomorphism of the Tate modules. The next theorem allows us to extract information from the Tate modules to get information about the isogenies. We will see more of this idea in the next chapter.
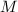 of
of 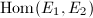 , we claim that the group
, we claim that the group 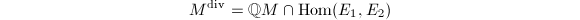 is also finitely generated. We can extend the degree map continuously to
is also finitely generated. We can extend the degree map continuously to 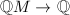 . Then
. Then 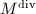 is discrete in
is discrete in 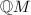 , since every isogeny has degree at least one. So
, since every isogeny has degree at least one. So 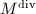 is a discrete subgroup of a finite-dimensional vector space
is a discrete subgroup of a finite-dimensional vector space 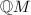 and thus must be finitely generated. This proves the claim.
and thus must be finitely generated. This proves the claim.
Step 2 Because 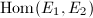 is torsion-free, we have
is torsion-free, we have ![$$M^{\mathrm{div}}=\{\phi\in\Hom(E_1,E_2): [m]\circ\phi\in M \text{ for some integer } m\ge1\}.$$](./latex/latex2png-MinorThesis1_47033512_.gif) Since
Since 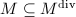 and
and 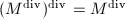 , it suffices to show that for each finitely generated subgroup
, it suffices to show that for each finitely generated subgroup 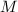 such that
such that 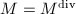 , the natural map
, the natural map 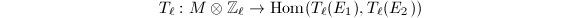 is injective. Since
is injective. Since 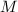 is finitely generated and torsion-free, it is free. Let
is finitely generated and torsion-free, it is free. Let 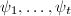 be a basis for
be a basis for 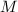 and
and 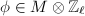 . We can write
. We can write 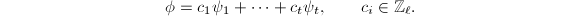 Now suppose
Now suppose 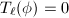 , then for each
, then for each 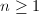 , there exist integers
, there exist integers 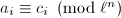 such that
such that 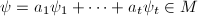 annihilates
annihilates ![$E_1[\ell^n]$](./latex/latex2png-MinorThesis1_233210925_-5.gif) . Hence
. Hence 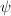 factors through
factors through ![$[\ell^n]$](./latex/latex2png-MinorThesis1_48858154_-5.gif) since
since ![$[\ell^n]$](./latex/latex2png-MinorThesis1_48858154_-5.gif) is separable, namely there exists
is separable, namely there exists 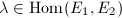 such that
such that ![$\psi=[\ell^n]\circ \lambda$](./latex/latex2png-MinorThesis1_258995696_-5.gif) . Therefore
. Therefore 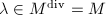 . We can write
. We can write ![$$\lambda=[b_1]\circ \psi_1+\cdots+[b_t]\circ \psi_t,\qquad b_i\in\mathbb{Z}.$$](./latex/latex2png-MinorThesis1_121970205_.gif) Now
Now ![$\psi=[\ell^n]\circ\psi$](./latex/latex2png-MinorThesis1_240424330_-5.gif) implies that
implies that 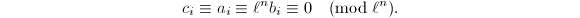 But
But 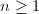 is arbitrary, so then
is arbitrary, so then 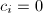 and
and 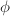 itself is zero. This completes the proof of the injectivity of
itself is zero. This completes the proof of the injectivity of 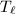 .
¡õ
.
¡õ
Now the following consequence is relatively easy and less surprising.
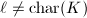 be a prime. Since
be a prime. Since 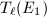 and
and 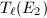 are both isomorphic to
are both isomorphic to 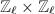 , hence
, hence 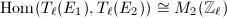 is a rank 4 free
is a rank 4 free 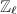 -module. Using the injectivity in Theorem 5 we know that
-module. Using the injectivity in Theorem 5 we know that 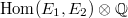 is a
is a 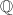 -vector space of dimension at most 4, hence
-vector space of dimension at most 4, hence 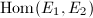 , as a discrete subgroup of
, as a discrete subgroup of 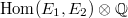 , is a free
, is a free 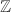 -module and has rank at most 4. (Added 2021/02/03: thank Carlo Pagano for correction of this proof.)
¡õ
-module and has rank at most 4. (Added 2021/02/03: thank Carlo Pagano for correction of this proof.)
¡õ
We are now in a position to prove the three possibilities for the endomorphism ring of an elliptic curve mentioned in the beginning of this chapter, i.e., the integers 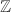 , an order in an imaginary quadratic extension of
, an order in an imaginary quadratic extension of 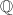 , or an order in a quaternion algebra over
, or an order in a quaternion algebra over 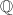 . Let us make precise the meaning of a quaternion algebra.
. Let us make precise the meaning of a quaternion algebra.
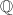 is an four-dimensional
is an four-dimensional 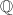 -algebra generated by
-algebra generated by 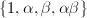 whose multiplication satisfies
whose multiplication satisfies 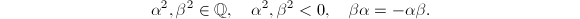
Keep in mind that we will apply the following little tricky theorem to 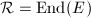 and
and  as the dual isogeny.
as the dual isogeny.
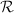 be a (not necessarily commutative) ring of characteristic zero having no zero divisors. Assume
be a (not necessarily commutative) ring of characteristic zero having no zero divisors. Assume 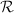 has the following properties:
has the following properties:
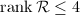 .
.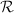 has an involution
has an involution 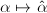 such that for any
such that for any 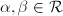 and
and 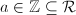 ,
, 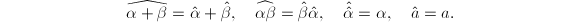
- For any
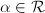 ,
, 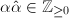 . Moreover,
. Moreover, 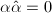 if and only if
if and only if 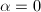 .
.
Then 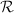 is of one of the following types:
is of one of the following types:
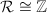 .
.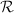 is an order in an imaginary quadratic extension of
is an order in an imaginary quadratic extension of 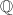 .
.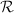 is an order in a quaternion algebra over
is an order in a quaternion algebra over 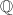 .
.
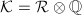 , it suffices to show that
, it suffices to show that 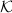 is either
is either 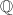 , an imaginary quadratic extension of
, an imaginary quadratic extension of 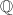 or a quaternion algebra over
or a quaternion algebra over 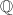 . Define the norm map and trace map from
. Define the norm map and trace map from 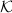 to
to 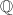 using the involution,
using the involution, 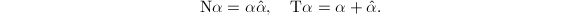 Then
Then 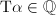 since
since 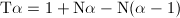 . Suppose
. Suppose 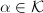 such that
such that 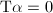 , then
, then 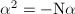 since
since 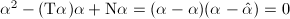 . So if
. So if 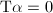 and
and 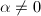 then
then 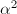 is a negative rational number.
is a negative rational number.
If 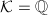 , we are done.
, we are done.
Otherwise, we can find 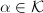 such that
such that 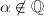 . Replacing
. Replacing 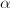 by
by 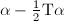 we may assume
we may assume 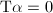 . Hence
. Hence 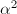 is a negative rational number. If
is a negative rational number. If 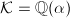 , then we are done.
, then we are done.
Otherwise, we can find 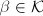 such that
such that 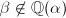 . Replacing
. Replacing 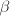 by
by 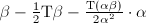 , we may assume
, we may assume 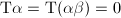 . Hence
. Hence 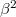 is also a negative rational number and
is also a negative rational number and 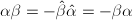 . Now it suffices to show that
. Now it suffices to show that 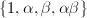 is linearly independent over
is linearly independent over 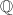 to complete the proof.
to complete the proof.
Suppose there is a linear relation 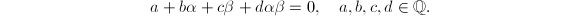 Taking the trace we get
Taking the trace we get 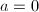 . Multiplying by
. Multiplying by 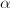 on the left and
on the left and 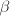 on the right and using
on the right and using 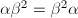 , we obtain
, we obtain 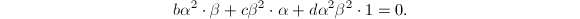 But
But 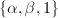 are linearly independent over
are linearly independent over 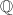 by construction, which implies that
by construction, which implies that 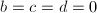 . This completes the proof.
¡õ
. This completes the proof.
¡õ
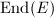 of an elliptic curve
of an elliptic curve 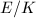 is either
is either 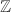 , an order in an imaginary quadratic extension of
, an order in an imaginary quadratic extension of 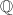 , or an order in a quaternion algebra over
, or an order in a quaternion algebra over 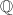 . Moreover, only the first two cases are possible when
. Moreover, only the first two cases are possible when 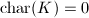 .
.
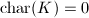 ,
, 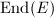 is commutative by Theorem 4, hence the third case is impossible.
¡õ
is commutative by Theorem 4, hence the third case is impossible.
¡õ
 is defined over a finite field, then
is defined over a finite field, then 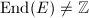 (Theorem 4), so only the latter two cases can happen.
(Theorem 4), so only the latter two cases can happen.
Elliptic curves with different endomorphism rings behave fundamentally differently in many aspects, so various terminologies were invented.
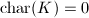 , then we say that an elliptic curve
, then we say that an elliptic curve 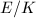 has complex multiplication or (historically) that
has complex multiplication or (historically) that  is singular, if
is singular, if 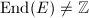 . If
. If 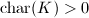 , we say that
, we say that 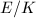 is supersingular if
is supersingular if 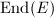 is an order in a rational quaternion algebra, otherwise we say that
is an order in a rational quaternion algebra, otherwise we say that  is ordinary.
is ordinary.
By now we have achieved our goal of giving a primary classification of the endomorphism rings of elliptic curves in this chapter. In the next chapter we will concentrate more on the positive characteristic case. In particular, we will give a refined characterization of the endomorphism rings of supersingular elliptic curves using more useful tools and deep results.
References
[1]The Arithmetic of Elliptic Curves, Springer, 2010.
[2]Advanced Topics in the Arithmetic of Elliptic Curves, Springer, 1994.
[3]Introduction to Algebraic Curves, American Mathematical Society, 1989.
![$E[p^r]$](./latex/latex2png-MinorThesis1_50306241_-5.gif) and
and 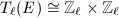 .
.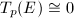 or
or 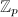 .
.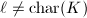 be a prime. Then the natural map
be a prime. Then the natural map 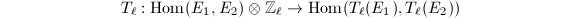 is injective.
is injective.