We give an overview of Lusztig's classification of irreducible representations of reductive groups over finite fields and provide explicit examples. The parametrization involves a semisimple conjugacy class of the dual group and a unipotent representation of its centralizer, in a spirit similar to Langlands parameters for irreducible admissible representations of reductive groups over local fields.
This is a note prepared for an Alcove Seminar talk at Harvard, Spring 2015. Our main reference is [1].
 Dual groups and the Jordan decomposition
Dual groups and the Jordan decomposition
Let 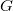 be a connected reductive group over
be a connected reductive group over 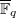 together with a Frobenius map
together with a Frobenius map 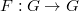 defining a
defining a 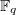 -structure on
-structure on 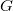 . Recall that the main theorem of Deligne-Lusztig says that every irreducible representation (over
. Recall that the main theorem of Deligne-Lusztig says that every irreducible representation (over 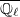 ) of the finite group
) of the finite group 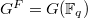 appears in the Deligne-Lusztig induction
appears in the Deligne-Lusztig induction 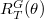 for some
for some 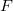 -stable (i.e., defined over
-stable (i.e., defined over 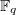 ) maximal torus
) maximal torus 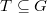 and some character
and some character 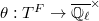 . Moreover, when
. Moreover, when  is in general position (i.e.,
is in general position (i.e., 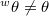 for any nontrivial element
for any nontrivial element 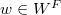 , where
, where 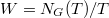 is the Weyl group),
is the Weyl group), 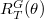 is the character (up to sign) of an irreducible representation of
is the character (up to sign) of an irreducible representation of 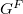 .
.
To construct the remaining irreducible representations of 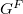 , one needs to further decompose reducible Deligne-Lusztig characters
, one needs to further decompose reducible Deligne-Lusztig characters 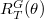 , which can be done using Howlett-Lehrer theory nowadays. After obtaining all irreducible representations, one also hopes to parametrize them in a structural manner so that one can actually use the classification in practice.
, which can be done using Howlett-Lehrer theory nowadays. After obtaining all irreducible representations, one also hopes to parametrize them in a structural manner so that one can actually use the classification in practice.
The first step of Lusztig's parametrization deals with the pair 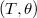 appeared in the Deligne-Lusztig characters. Recall that if two pairs
appeared in the Deligne-Lusztig characters. Recall that if two pairs 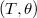 ,
, 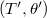 are not
are not 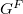 -conjugate, then
-conjugate, then 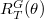 and
and 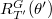 are orthogonal to each other. However, it may happen that
are orthogonal to each other. However, it may happen that 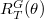 and
and 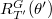 share the same irreducible factors (since they are virtual characters). To ensure that they don't share any irreducible factors, one needs the stronger notion of geometric conjugacy classes.
share the same irreducible factors (since they are virtual characters). To ensure that they don't share any irreducible factors, one needs the stronger notion of geometric conjugacy classes.
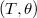 ,
, 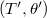 are geometrically conjugate if there exists some
are geometrically conjugate if there exists some  such that
such that 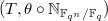 and
and 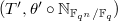 are
are 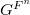 -conjugate.
-conjugate.
By [2, Cor 6.3], if two pairs 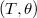 and
and 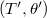 are not geometrically conjugate, then
are not geometrically conjugate, then 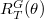 and
and 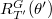 are disjoint. So the first step is to classify geometric conjugacy classes of the pair
are disjoint. So the first step is to classify geometric conjugacy classes of the pair 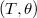 . This is neatly done using the dual group
. This is neatly done using the dual group 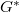 of
of 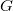 . The dual group
. The dual group 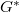 is a reductive group over
is a reductive group over 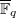 with the dual root datum and the dual Frobenius
with the dual root datum and the dual Frobenius 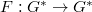 (defining an
(defining an 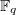 -structure on
-structure on 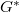 ). Notice this is not the Langlands dual group, which is defined over
). Notice this is not the Langlands dual group, which is defined over 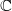 . By the very definition, the geometric conjugacy classes of
. By the very definition, the geometric conjugacy classes of 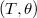 then correspond bijectively to geometric conjugacy classes of semisimple elements of
then correspond bijectively to geometric conjugacy classes of semisimple elements of 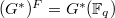 .
.
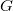 further has connected center, then by a theorem of Steinberg, (the derived group of)
further has connected center, then by a theorem of Steinberg, (the derived group of) 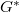 is simply-connected (up to inseparable coverings) and the centralizer of a semisimple element of
is simply-connected (up to inseparable coverings) and the centralizer of a semisimple element of 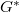 is connected. Hence by Lang's theorem, there is no distinction between conjugacy classes and geometric conjugacy classes, hence the geometric conjugacy classes of
is connected. Hence by Lang's theorem, there is no distinction between conjugacy classes and geometric conjugacy classes, hence the geometric conjugacy classes of 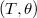 correspond bijectively to conjugacy classes of semisimple elements of
correspond bijectively to conjugacy classes of semisimple elements of 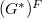 . We will assume
. We will assume 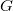 has connected center for simplicity from now on.
has connected center for simplicity from now on.
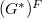 has size
has size 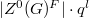 , where
, where 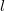 is the semisimple rank of
is the semisimple rank of 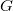 ([2, 5.6 (ii)]).
([2, 5.6 (ii)]).
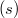 be a semisimple conjugacy class of the dual group
be a semisimple conjugacy class of the dual group 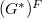 , the Lusztig series
, the Lusztig series 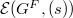 is the set of irreducible representations of
is the set of irreducible representations of 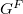 appearing in
appearing in 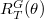 for any pair
for any pair 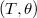 corresponding to
corresponding to 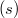 .
.
In particular, the Lusztig series 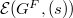 form a disjoint partition of
form a disjoint partition of 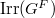 . The second step is to parametrize each Lusztig series.
. The second step is to parametrize each Lusztig series.
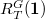 where
where 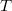 runs over all
runs over all 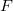 -stable maximal torus. As we will see very soon, these unipotent representations are closely related to unipotent conjugacy classes.
-stable maximal torus. As we will see very soon, these unipotent representations are closely related to unipotent conjugacy classes.
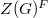 acts trivially on the Deligne-Lusztig varieties and thus lies in the kernel of every unipotent representation of
acts trivially on the Deligne-Lusztig varieties and thus lies in the kernel of every unipotent representation of 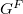 .
.
When 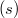 is regular semisimple,
is regular semisimple, 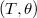 is in general position and hence the Lusztig series is a singleton. When
is in general position and hence the Lusztig series is a singleton. When 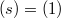 is trivial, the Lusztig series consists of the unipotent representations of
is trivial, the Lusztig series consists of the unipotent representations of 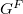 . When
. When 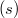 lies between the two extremal cases, it turns out that the Lusztig series
lies between the two extremal cases, it turns out that the Lusztig series 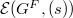 can be parametrized by the unipotent representations of a smaller connected reductive group
can be parametrized by the unipotent representations of a smaller connected reductive group 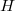 , where
, where 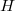 is the dual of the centralizer
is the dual of the centralizer 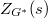 ([3, Theorem 4.23]).
([3, Theorem 4.23]).
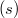 be a semisimple conjugacy class of
be a semisimple conjugacy class of 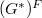 and
and 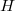 be the dual group of the centralizer
be the dual group of the centralizer 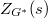 . Then there is a bijection
. Then there is a bijection 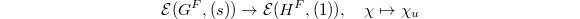 such that for any pair
such that for any pair 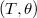 corresponding to
corresponding to 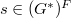 ,
, 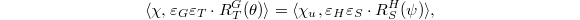 where
where  is any pair corresponding to
is any pair corresponding to  and
and  .
.
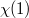 is (up to sign) the product of
is (up to sign) the product of 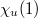 and the prime-to-
and the prime-to-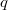 part of
part of 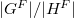 . The latter is exactly the degree of the unique semisimple character
. The latter is exactly the degree of the unique semisimple character 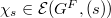 associated to
associated to 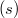 ([1, 8.4.8]). So this theorem can be thought of as a Jordan decomposition for irreducible representations. We remark that the construction of the bijection is done case by case after decomposing all the Deligne-Lusztig characters
([1, 8.4.8]). So this theorem can be thought of as a Jordan decomposition for irreducible representations. We remark that the construction of the bijection is done case by case after decomposing all the Deligne-Lusztig characters 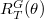 .
.
By induction, the problem remaining is to parametrize the unipotent representations for any connected reductive group 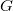 . This is done case by case in Lusztig's several papers and books ([4],[5],[6], [7],[8], [9]). We aim to summarize his results.
. This is done case by case in Lusztig's several papers and books ([4],[5],[6], [7],[8], [9]). We aim to summarize his results.
 Unipotent representations
Unipotent representations
Classifying all unipotent representations again uses an inductive strategy in terms of unipotent cuspidal representations and parabolic induction. For each classical group, there is either no or only one unipotent cuspidal representation. The cases for which there exists one unipotent cuspidal representation are listed as follows.
![\begin{center}
\begin{tabular}[h]{*{8}{|>{$}c<{$}}|}\hline
B_l & C_l & D_l & ^2A_l & ^2D_l \\\hline
l=s^2+s &
l=s^2+s & l=s^2, 2\mid s & l=\frac{1}{2}(s^2+s)-1 & l=s^2, 2\nmid s\\\hline
\end{tabular}
\end{center}](./latex/latex2png-LusztigClassification_1960470_.gif)
For each exceptional group, there are at least two unipotent cuspidal representations. The number of unipotent cuspidal representations and the total number of unipotent representations are listed as follows.
![\begin{center}
\begin{tabular}[h]{*{10}{|>{$}c<{$}}|}\hline
E_6 & E_7 & E_8 & F_4 & G_2 & ^3D_4 & ^2E_6 & ^2B_2 & ^2G_2 & ^2F_4\\\hline
2 & 2 & 13 & 7 & 4 & 2 & 3 & 2 & 6 & 10\\\hline
30 & 76 & 166 & 37 & 10 & 8 & 30 & 4 & 8 & 21 \\\hline
\end{tabular}
\end{center}](./latex/latex2png-LusztigClassification_217138825_.gif)
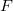 -eigenspaces of the middle cohomology
-eigenspaces of the middle cohomology 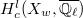 of the Deligne-Lusztig varieties associated to the Coxeter element
of the Deligne-Lusztig varieties associated to the Coxeter element 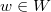 ([10]). In each case Lusztig was able to find most of the unipotent cuspidal representations. He then counted the number unipotent representations thus obtained. Together with a formula for the sum of the squares of the dimension of unipotent representations, he concluded that a very small number of unipotent cuspidal representation is missing: 3 for
([10]). In each case Lusztig was able to find most of the unipotent cuspidal representations. He then counted the number unipotent representations thus obtained. Together with a formula for the sum of the squares of the dimension of unipotent representations, he concluded that a very small number of unipotent cuspidal representation is missing: 3 for 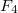 , 7 for
, 7 for 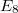 and at most one in the other cases (which also explains the extra cases for classical groups). The remaining cuspidal ones are then constructed case by case using brutal force.
and at most one in the other cases (which also explains the extra cases for classical groups). The remaining cuspidal ones are then constructed case by case using brutal force.
After all the unipotent representations are obtained, Lusztig observed that they naturally form families in a remarkable way, parametrized by special unipotent conjugacy classes (justifying the name).
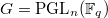 . It was known from Green's work that each irreducible unipotent character of
. It was known from Green's work that each irreducible unipotent character of 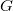 is of the form
is of the form
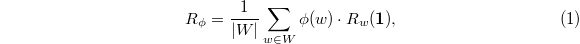 a linear combination of the Deligne-Lusztig characters
a linear combination of the Deligne-Lusztig characters 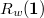 weighted by an irreducible character
weighted by an irreducible character 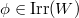 of the Weyl group
of the Weyl group 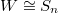 . This gives a bijection between unipotent representations of
. This gives a bijection between unipotent representations of 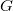 and
and 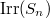 . On the other hand, the irreducible representations of
. On the other hand, the irreducible representations of 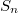 is in bijection with the partitions of
is in bijection with the partitions of 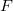 , hence is in bijection with unipotent conjugacy classes of
, hence is in bijection with unipotent conjugacy classes of 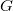 (= shape of Jordan blocks)! In particular, the unipotent representations should be parametrized in a way that is independent of
(= shape of Jordan blocks)! In particular, the unipotent representations should be parametrized in a way that is independent of 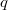 !
!
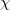 and
and 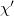 are in the same family if there exists a chain of characters
are in the same family if there exists a chain of characters 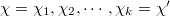 and
and 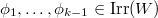 such that
such that 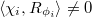 and
and 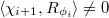 .
.
It turns out that something stronger is true: for a family 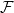 , there exists a unique
, there exists a unique 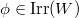 such that
such that 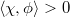 for any
for any 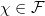 . This gives a bijection between families and a subset of
. This gives a bijection between families and a subset of 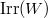 , called special characters of
, called special characters of 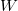 . All characters are special for type
. All characters are special for type 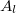 , but not for other types of groups. By the Springer correspondence, there is a bijection between
, but not for other types of groups. By the Springer correspondence, there is a bijection between 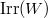 and certain pairs
and certain pairs 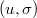 , where
, where 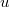 is a unipotent conjugacy class of
is a unipotent conjugacy class of 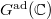 and
and 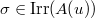 (here
(here 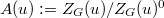 ). Moreover, even though
). Moreover, even though 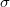 may be nontrivial, it turns out that the set of unipotent classes of
may be nontrivial, it turns out that the set of unipotent classes of 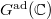 injects into
injects into 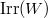 . Those unipotent classes corresponding to the special characters of
. Those unipotent classes corresponding to the special characters of 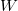 are naturally called special unipotent.
are naturally called special unipotent.
Now Lusztig's parameter for an irreducible representation of 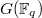 consists of a semisimple conjugacy class
consists of a semisimple conjugacy class 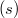 of
of 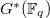 and a special unipotent conjugacy class
and a special unipotent conjugacy class 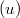 of
of 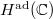 , where
, where 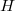 is the Langlands dual group of
is the Langlands dual group of 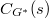 . The shape of Lusztig's parameters is a reminisce of local Langlands parameters: the Weil group of
. The shape of Lusztig's parameters is a reminisce of local Langlands parameters: the Weil group of 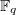 is simply
is simply 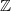 and a homomorphism from the Weil group to
and a homomorphism from the Weil group to 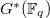 corresponds to a semisimple class
corresponds to a semisimple class 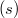 . However,
. However, 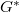 is not the Langlands dual group and one needs to add the adjective special to the complex unipotent class
is not the Langlands dual group and one needs to add the adjective special to the complex unipotent class 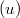 .
.
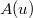 is an elementary 2-group
is an elementary 2-group 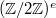 when
when 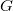 is of classical type and is a symmetric group on
is of classical type and is a symmetric group on 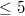 letters when
letters when 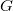 is of exceptional type. Miraculously, the members of a family
is of exceptional type. Miraculously, the members of a family 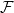 can be parameterized by pairs
can be parameterized by pairs 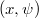 , where
, where 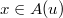 and
and 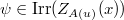 . Families thus can be thought as analogues of
. Families thus can be thought as analogues of 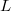 -packets. Notice that
-packets. Notice that 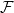 has size 1,
has size 1, 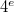 , 8, 21 or 39 according to
, 8, 21 or 39 according to 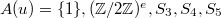 . (Added on 04/18/2016: as Cheng-Chiang pointed out to me, this is not quite true. The correct statement is to replace
. (Added on 04/18/2016: as Cheng-Chiang pointed out to me, this is not quite true. The correct statement is to replace 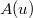 appearing in this remark by a certain quotient of
appearing in this remark by a certain quotient of 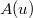 known as Lusztig quotient group.)
known as Lusztig quotient group.)
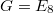 , there are 46 families of unipotent characters corresponding to the 46 special representations of the Weyl group
, there are 46 families of unipotent characters corresponding to the 46 special representations of the Weyl group 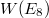 . There are 23 families with 1 character, 18 families with 4 characters, 4 families with 8 characters, and one family with 39 characters, which gives a total number of
. There are 23 families with 1 character, 18 families with 4 characters, 4 families with 8 characters, and one family with 39 characters, which gives a total number of 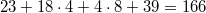 unipotent representations.
unipotent representations.
 Examples
Examples
For classical groups, Lusztig parametrized the unipotent representations using symbols, a combinatorial gadget (independent of 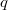 ) corresponding to special characters of
) corresponding to special characters of 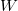 .
.
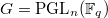 . As in Example 1, the symbols are simply partitions of
. As in Example 1, the symbols are simply partitions of 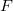 . The partition
. The partition  corresponds to the trivial representation of
corresponds to the trivial representation of 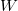 and the trivial representation of
and the trivial representation of 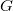 . The partition
. The partition  corresponds to the sign representation of
corresponds to the sign representation of  and the Steinberg representation of
and the Steinberg representation of 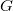 , which has dimension
, which has dimension 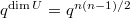 (
(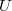 is the maximal unipotent subgroup of
is the maximal unipotent subgroup of 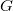 ). For a general partition
). For a general partition 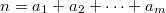 ,
, 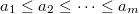 . Let
. Let 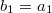 ,
, 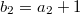 ,
, 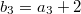 and so on. Then the corresponding unipotent representation has dimension
and so on. Then the corresponding unipotent representation has dimension 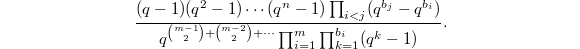 For example,
For example,
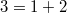 corresponds to the standard representation of
corresponds to the standard representation of 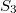 of dimension 2. The corresponding unipotent representation has dimension
of dimension 2. The corresponding unipotent representation has dimension 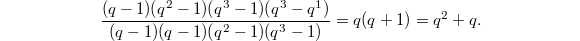
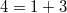 corresponds to the standard representation of
corresponds to the standard representation of 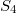 of dimension 3. The corresponding unipotent representation has dimension
of dimension 3. The corresponding unipotent representation has dimension 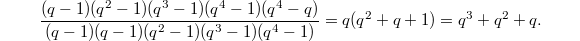
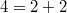 corresponds to the 2-dimensional representation of
corresponds to the 2-dimensional representation of 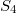 . The corresponding unipotent representation has dimension
. The corresponding unipotent representation has dimension 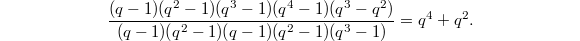
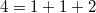 corresponds to the twisted (by the sign character) standard representation of
corresponds to the twisted (by the sign character) standard representation of 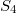 . The corresponding unipotent representation has dimension
. The corresponding unipotent representation has dimension 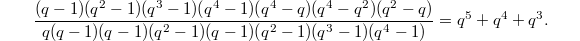
We conclude that
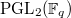 has 2 unipotent representations: they have dimension 1 and
has 2 unipotent representations: they have dimension 1 and 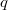 .
.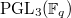 has 3 unipotent representations: they have dimension 1,
has 3 unipotent representations: they have dimension 1, 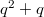 , and
, and 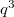 .
.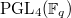 has 5 unipotent representations: they have dimension 1,
has 5 unipotent representations: they have dimension 1, 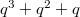 ,
, 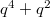 ,
, 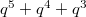 ,
, 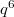 .
.
It could be a lot of fun to check the identity computing the number of 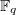 -points of the flag variety
-points of the flag variety 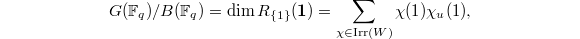 where
where 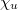 is the unipotent character corresponding to the special character
is the unipotent character corresponding to the special character 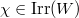 . For example, when
. For example, when 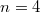 this says
this says 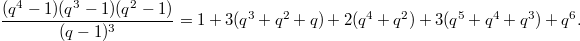
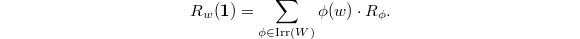 We see that the parabolic induction is
We see that the parabolic induction is 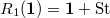 and the Deligne-Lusztig induction (realized on the Drinfeld curve) is
and the Deligne-Lusztig induction (realized on the Drinfeld curve) is 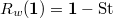 . See Drinfeld curves for an elementary introduction.
. See Drinfeld curves for an elementary introduction.
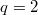 ,
, 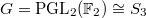 . The two unipotent representations are the trivial representations and the 2-dimensional representation. There is a unique cuspidal representation, the sign representation of
. The two unipotent representations are the trivial representations and the 2-dimensional representation. There is a unique cuspidal representation, the sign representation of 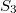 . A cool consequence: the local representation at 2 of any elliptic curve over
. A cool consequence: the local representation at 2 of any elliptic curve over 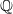 with conductor
with conductor 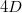 is the unique depth zero supercuspidal representation of
is the unique depth zero supercuspidal representation of 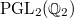 , i.e., the compact induction of the
, i.e., the compact induction of the 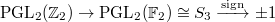 .
.
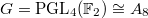 . Using the hook-length formula we find that it has the irreducible representations of the following dimensions: 1, 7, 14, 20 ,21, 21, 21, 28, 35, 45, 45, 56, 64, 70. We check this using Lusztig's classification (plug in
. Using the hook-length formula we find that it has the irreducible representations of the following dimensions: 1, 7, 14, 20 ,21, 21, 21, 28, 35, 45, 45, 56, 64, 70. We check this using Lusztig's classification (plug in 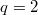 in the previous example).
in the previous example).
![\begin{center}
\begin{tabular}[h]{*{4}{|>{$}c<{$}}|}\hline
(s) & H & |\chi_s(1)|=\frac{|G^F|}{|H^F|}_{q'} & |\chi_u(1)\cdot\chi_s(1)|\\\hline
\diag\{1,1,1,1\} & \PGL_4 & 1 & 1, 14, 20, 56, 64\\\hline
\diag\{\zeta_3,\zeta_3^2, 1,1\} & \PGL_2\times\mu_3 & \frac{15\cdot 7\cdot 3}{3 \cdot 3}=35 & 35, 70\\\hline
\diag\{\zeta_3, \zeta_3^2, \zeta_3,\zeta_3^2\} & {\PGL_2}_{/\mathbb{F}_4} & \frac{15\cdot 7\cdot 3}{15 \cdot 3}=7 & 7, 28 \\\hline
\diag\{\zeta_7, \zeta_7^2,\zeta_7^4, 1\} & \mu_7 & \frac{15\cdot 7\cdot 3}{7}=45 & 45, 45\\\hline
\diag\{\zeta_{15},\zeta_{15}^2, \zeta_{15}^4, \zeta_{15}^8\} & \mu_{15} & \frac{15\cdot 7\cdot 3}{15}= 21 & 21,21,21\\\hline
\end{tabular}
\end{center}](./latex/latex2png-LusztigClassification_223759273_.gif)
In particular, we see that there are three cuspidal representations, all of them have dimension 21.
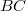 to be a tuple
to be a tuple 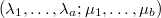 , where
, where 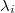 ,
, 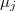 are non-negative and strictly increasing,
are non-negative and strictly increasing, 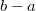 is a positive odd integer, and
is a positive odd integer, and 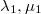 are not both zero. Define the rank of this symbol by
are not both zero. Define the rank of this symbol by 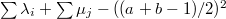 . Then there is a bijection between unipotent characters of type
. Then there is a bijection between unipotent characters of type 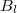 and
and 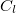 and symbols of rank
and symbols of rank 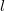 . There is a similar formula for the dimension of the corresponding unipotent character as that for type
. There is a similar formula for the dimension of the corresponding unipotent character as that for type 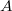 . A unipotent character with
. A unipotent character with 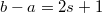 appears in the parabolic induction of the unique unipotent cuspidal representation of
appears in the parabolic induction of the unique unipotent cuspidal representation of 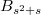 or
or 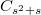 . The unipotent characters fall into families according to the multi-set
. The unipotent characters fall into families according to the multi-set 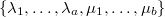 .
.
For example, consider 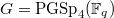 . There are 6 symbols of rank 2, corresponding to 6 unipotent representations with the following dimensions:
. There are 6 symbols of rank 2, corresponding to 6 unipotent representations with the following dimensions:
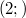 , 1 (trivial);
, 1 (trivial);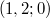 ,
, 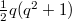 ;
;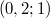 ,
, 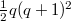 ;
;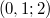 ,
, 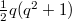 ;
; ,
, 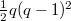 (unipotent cuspidal);
(unipotent cuspidal);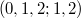 ,
, 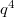 (Steinberg).
(Steinberg).
They form families of size 1, 4 and 1.
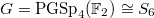 . Using the hook-length formula we find that it has irreducible representations of the following dimensions: 1, 1, 5, 5, 5, 5, 9, 9, 10, 10, 16. We check this using Lusztig's classification (plug in
. Using the hook-length formula we find that it has irreducible representations of the following dimensions: 1, 1, 5, 5, 5, 5, 9, 9, 10, 10, 16. We check this using Lusztig's classification (plug in 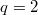 in the previous example).
in the previous example).
![\begin{center}
\begin{tabular}[h]{*{4}{|>{$}c<{$}}|}\hline
(s) & H & |\chi_s(1)|=\frac{|G^F|}{|H^F|}_{q'} & |\chi_u(1)\cdot\chi_s(1)|\\\hline
\diag\{1,1,1,1\} & \PGSp_4 & 1 & 1, 5, 9, 5, 1, 16\\\hline
\diag\{\zeta_3,1, \zeta_3^{-1},1\} & \PGL_2\times\mu_3 & \frac{5 \cdot 3 \cdot 3}{3 \cdot 3}=5 & 5, 10\\\hline
\diag\{\zeta_3,\zeta_3^2, \zeta_3^{-1},\zeta_3^{-2}\} & \mathrm{U}_2 & \frac{5 \cdot 3 \cdot 3}{3 \cdot 3}=5 & 5, 10\\\hline
\diag\{\zeta_{5},\zeta_{5}^2, \zeta_{5}^{-1}, \zeta_{5}^{-2}\} & \mu_{5} & \frac{5\cdot 3\cdot 3}{5}= 9 & 9\\\hline
\end{tabular}
\end{center}](./latex/latex2png-LusztigClassification_100271569_.gif)
In particular, there are two cuspidal representations: they have dimension 1 (unipotent, the sign character of 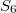 ) and 9.
) and 9.
References
[1]Finite groups of Lie type, John Wiley \& Sons, Inc., New York, 1985.
[2]Representations of reductive groups over finite fields, Ann. of Math. (2) 103 (1976), no.1, 103--161.
[3]Characters of reductive groups over a finite field, Princeton University Press, Princeton, NJ, 1984.
[4]Irreducible representations of finite classical groups, Invent. Math. 43 (1977), no.2, 125--175.
[5]Representations of finite Chevalley groups, American Mathematical Society, Providence, R.I., 1978.
[6]Unipotent representations of a finite Chevalley group of type $E_8$, Quart. J. Math. Oxford Ser. (2) 30 (1979), no.119, 315--338.
[7]On the unipotent characters of the exceptional groups over finite fields, Invent. Math. 60 (1980), no.2, 173--192.
[8]Unipotent characters of the symplectic and odd orthogonal groups over a finite field, Invent. Math. 64 (1981), no.2, 263--296.
[9]Unipotent characters of the even orthogonal groups over a finite field, Trans. Amer. Math. Soc. 272 (1982), no.2, 733--751.
[10]Coxeter orbits and eigenspaces of Frobenius, Invent. Math. 38 (1976/77), no.2, 101--159.
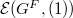 are called unipotent representations.
are called unipotent representations.
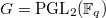 . We list Lusztig's parametrization as follows.
. We list Lusztig's parametrization as follows.
![\begin{center}
\begin{tabular}[h]{*{4}{|>{$}c<{$}}|}\hline
(s) & H & |\chi_s(1)|=\frac{|G^F|}{|H^F|}_{q'} & |\chi_u(1)\cdot\chi_s(1)|\\\hline
\diag\{1,1\} & \PGL_2 & 1 & 1 \text{(trivial)}, q \text{(Steinberg)}\\\hline
\diag\{\zeta_{q-1},1\} & \mu_{q-1} & q+1 & q+1 \text{(principal series)} \\\hline
\diag\{\zeta_{q+1}, \zeta_{q+1}^q\} & \mu_{q+1} & q-1 & q-1 \text{(cuspidal)} \\\hline
\end{tabular}
\end{center}](./latex/latex2png-LusztigClassification_141301626_.gif)