Drinfeld, at the age of 20, discovered that the discrete series representations of the finite group 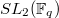 can be realized in the
can be realized in the  -adic cohomology of the curve defined over
-adic cohomology of the curve defined over 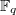 ,
, 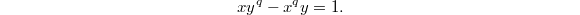 Deligne and Lusztig were inspired by this result to associate algebraic varieties to any finite group of Lie type and were extremely successful in using them to construct all representations of such a finite group. We will explain their beautiful ideas and supply concrete examples of Deligne-Lusztig curves. These curves themselves also enjoy extremal geometric and arithmetic properties, which, among others, lead us to contemplate on the answer to life, the universe and everything.
Deligne and Lusztig were inspired by this result to associate algebraic varieties to any finite group of Lie type and were extremely successful in using them to construct all representations of such a finite group. We will explain their beautiful ideas and supply concrete examples of Deligne-Lusztig curves. These curves themselves also enjoy extremal geometric and arithmetic properties, which, among others, lead us to contemplate on the answer to life, the universe and everything.
This is a note I prepared for my third Trivial Notions talk at Harvard, Fall 2013. Our main sources are [1], [2], [3], [4], [5] and [6].
My talk consists of two parts. In the first part I shall define our trivial notion in the title. In second part I shall explain how this definition makes sense.
This completes the first part of my talk. Surprisingly we still have enough time to do the second part. Now let us start with a completely different story.
 Finite groups of Lie types
Finite groups of Lie types
According to the classification of finite simple groups, except 26 sporadic groups, all finite simple groups fit into three infinite series
- a cyclic group
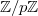 (of prime order);
(of prime order); - an alternating group
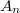 (
(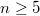 );
); - a simple finite group of Lie type.
A finite group of Lie type, as you can imagine, is a finite group analogue of Lie groups over real or complex numbers.
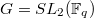 , where
, where 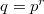 is a prime power. It is the fixed points of the standard Frobenius endomorphism
is a prime power. It is the fixed points of the standard Frobenius endomorphism 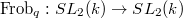 by raising each entry to the
by raising each entry to the 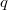 -th power, where
-th power, where 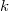 is an algebraic closure of
is an algebraic closure of 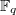 .
.
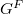 of an endomorphism
of an endomorphism 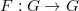 , where
, where 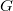 is any reductive group over
is any reductive group over 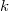 and a certain power of
and a certain power of 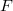 is a standard Frobenius
is a standard Frobenius 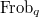 .
.
If you never care about algebraic varieties in positive characteristics, this probably serves as a reason that you probably should. After all these finite groups of Lie type form the major bulk of the building blocks of any finite group!
People familiar with Lie groups shall recall that the reductive groups over an algebraically closed field 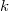 are classified by certain combinatoric data called root data, which are, roughly speaking, instructions telling you how to glue the building blocks
are classified by certain combinatoric data called root data, which are, roughly speaking, instructions telling you how to glue the building blocks 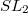 (and tori) to obtain
(and tori) to obtain 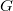 . These fit into 4 infinite series
. These fit into 4 infinite series 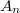 ,
, 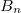 ,
, 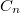 ,
, 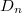 and five exceptional ones
and five exceptional ones 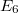 ,
, 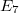 ,
, 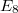 ,
, 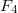 ,
, 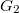 according to the associated Dynkin diagram (please refer to the picture on the wall outside 507 if you have good eyesight). For example,
according to the associated Dynkin diagram (please refer to the picture on the wall outside 507 if you have good eyesight). For example, 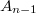 consists of the general linear group
consists of the general linear group 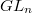 and its variations
and its variations 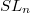 ,
, 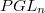 , and so on.
, and so on.
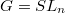 . For
. For 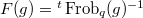 , we obtain
, we obtain 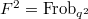 and
and 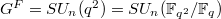 is the (unique) unitary group over
is the (unique) unitary group over 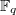 (
(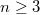 ). It is usually denoted by
). It is usually denoted by 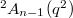 . The endomorphism
. The endomorphism  induces the involution of the Dynkin diagram
induces the involution of the Dynkin diagram 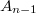 .
.
In general, such a endomorphism  induces an automorphism of the Dynkin diagram with arrow disregarded. Besides the
induces an automorphism of the Dynkin diagram with arrow disregarded. Besides the 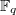 -points of the split groups (a.k.a., Chevalley groups), we have new series of finite groups of Lie type:
-points of the split groups (a.k.a., Chevalley groups), we have new series of finite groups of Lie type:
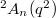 ,
, 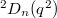 ,
, 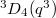 ,
, 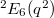 . These are
. These are 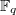 -points of the quasi-split forms of
-points of the quasi-split forms of 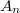 ,
, 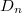 ,
, 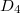 ,
, 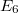 , known as Steinberg groups;
, known as Steinberg groups;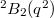 : Suzuki groups, exist only when
: Suzuki groups, exist only when 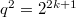 ;
;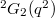 : Ree groups of type
: Ree groups of type 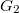 , exist only when
, exist only when 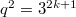 ;
;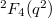 : Ree groups of type
: Ree groups of type 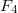 , exist only when
, exist only when 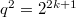 .
.
For the last three groups, the involution on the Dynkin diagram does not preserve the length of the roots and they are not 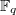 -points of any reductive groups! (You may want to think of them as points of a reductive group defined over a field of
-points of any reductive groups! (You may want to think of them as points of a reductive group defined over a field of 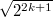 or
or 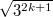 elements, which of course does not make sense).
elements, which of course does not make sense).
Now I have described the classification of finite groups of Lie type. You may find it interesting or simply don't care. But it will certainly become more interesting when a finite group 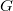 acts on objects that you care more about, e.g., topological spaces, manifolds, algebraic varieties... Linearizing such an action gives rise to a linear representation of
acts on objects that you care more about, e.g., topological spaces, manifolds, algebraic varieties... Linearizing such an action gives rise to a linear representation of 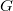 . So how can we understand all the irreducible representations of
. So how can we understand all the irreducible representations of 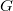 when
when 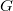 is a finite group of Lie type? Let us consider the simplest (but already rich enough) example
is a finite group of Lie type? Let us consider the simplest (but already rich enough) example 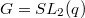 .
.
 Representations of
Representations of 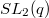
Over the complex numbers, the representation theory of any finite group 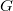 is rather clean: any finite dimensional representation of
is rather clean: any finite dimensional representation of 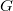 decomposes as a direct sum of irreducible subrepresentations. A representation
decomposes as a direct sum of irreducible subrepresentations. A representation 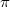 is characterized by its character
is characterized by its character 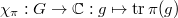 .
. 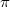 is irreducible if and only if
is irreducible if and only if 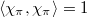 . The number of irreducible representations of
. The number of irreducible representations of 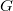 is the same as the number of conjugacy classes of
is the same as the number of conjugacy classes of 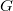 . And so on.
. And so on.
The conjugacy classes of 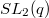 can be classified using elementary methods. For simplicity we shall assume that
can be classified using elementary methods. For simplicity we shall assume that 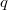 is odd. The representatives can be chosen as
is odd. The representatives can be chosen as
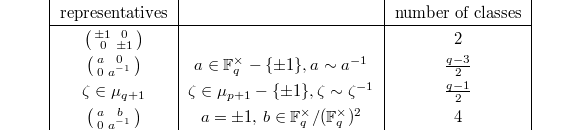
Notice 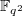 acts on
acts on 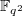 and produces a nonsplit torus
and produces a nonsplit torus 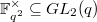 . Restricting to the norm one elements, we obtain
. Restricting to the norm one elements, we obtain 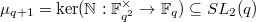 , a nonsplit torus of order
, a nonsplit torus of order 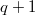 . Over
. Over 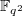 , its elements are conjugate to elements of the form
, its elements are conjugate to elements of the form 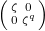 .
.
So in total we have 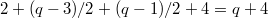 conjugacy classes. How do we construct
conjugacy classes. How do we construct 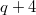 irreducible representations of
irreducible representations of 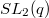 ? One usual way to build the character table of any finite group
? One usual way to build the character table of any finite group 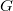 is to try to induce known representations of subgroups of
is to try to induce known representations of subgroups of 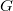 . A nice subgroup is given by the split diagonal torus
. A nice subgroup is given by the split diagonal torus 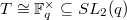 , which is a cyclic group of order
, which is a cyclic group of order  . The irreducible representations of
. The irreducible representations of 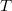 are simply the
are simply the  characters
characters 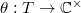 . But
. But 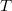 itself is too small which makes
itself is too small which makes 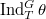 huge and far from irreducible. Instead we can view
huge and far from irreducible. Instead we can view 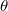 as a character on the Borel subgroup
as a character on the Borel subgroup 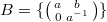 (trivial on the unipotent subgroup
(trivial on the unipotent subgroup 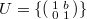 ). The resulting representation produced this way is called a parabolic induction.
). The resulting representation produced this way is called a parabolic induction.
- When
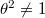 ,
, 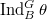 is irreducible of dimension
is irreducible of dimension 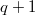 (principal series representations).
(principal series representations). - When
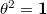 but
but 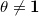 ,
, 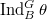 is a direct sum of two irreducible representations of dimension
is a direct sum of two irreducible representations of dimension 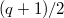 (half principal series representations).
(half principal series representations). - When
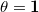 ,
, 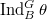 is a direct sum of the trivial representation and an irreducible representation of dimension
is a direct sum of the trivial representation and an irreducible representation of dimension 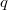 (the Steinberg representation).
(the Steinberg representation).
This gives us 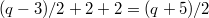 irreducible representations and there are
irreducible representations and there are 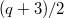 (about half) left to be discovered. It turns out
(about half) left to be discovered. It turns out 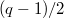 of them has dimension
of them has dimension  (discrete series representations) and 2 of them has dimension
(discrete series representations) and 2 of them has dimension 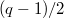 (half discrete series representations). Looking at the number
(half discrete series representations). Looking at the number 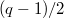 , one is tempted to induce a character of
, one is tempted to induce a character of 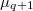 to construct the rest, but since there is no Borel subgroup containing it, there is no parabolic induction and the naive induction is more complicated than our expectation. Of course, one can mess around the character table and construct the discrete series representations using brutal force; but life would be harder for groups other than
to construct the rest, but since there is no Borel subgroup containing it, there is no parabolic induction and the naive induction is more complicated than our expectation. Of course, one can mess around the character table and construct the discrete series representations using brutal force; but life would be harder for groups other than 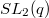 .
.
 The Drinfeld curve
The Drinfeld curve
If you are Drinfeld, then at this stage you must have realized that the right thing to look at is the affine curve 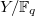 defined by the equation
defined by the equation 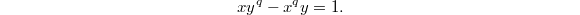 What is nice about it? First of all, the group
What is nice about it? First of all, the group 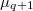 acts on it by
acts on it by 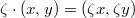 . More interestingly, it admits the action of
. More interestingly, it admits the action of 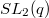 given by the linear transformation
given by the linear transformation 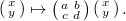 Indeed,
Indeed, 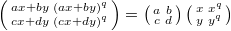 by characteristic
by characteristic 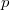 miracle and so fixes the determinant
miracle and so fixes the determinant 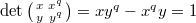 ! These two actions commute with each other and produce a large group of automorphisms of
! These two actions commute with each other and produce a large group of automorphisms of 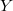 .
.
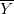 of the curve
of the curve 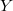 has genus
has genus 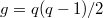 . But
. But 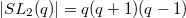 (indeed, a large group of order
(indeed, a large group of order 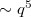 acts on
acts on 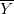 ) grows much quickly than
) grows much quickly than 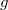 ! So when
! So when 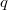 is large,
is large, 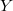 is an example of curves in positive characteristic violating the Hurwitz bound
is an example of curves in positive characteristic violating the Hurwitz bound 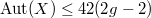 for curves
for curves 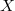 with
with 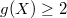 in characteristic 0. So the answer to life, the universe and everything may be something different if the universe has positive characteristic.
in characteristic 0. So the answer to life, the universe and everything may be something different if the universe has positive characteristic.
Let 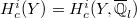 be
be  -adic etale cohomology groups with compact support of
-adic etale cohomology groups with compact support of 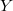 . Then the group
. Then the group 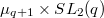 naturally acts on
naturally acts on 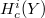 .
.
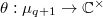 be a character. We define the Deligne-Lusztig induction of
be a character. We define the Deligne-Lusztig induction of 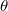 to be
to be ![$R(\theta)=H_c^*(Y)[\theta]=\sum_{i}(-1)^i H_c^i(Y)[\theta]$](./latex/DeligneLusztig/latex2png-DeligneLusztig_148236155_-5.gif) , a virtual character of
, a virtual character of 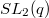 . Here
. Here ![$H_c^i(Y)[\theta]$](./latex/DeligneLusztig/latex2png-DeligneLusztig_36214744_-5.gif) denotes the
denotes the 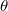 -isotypic component of
-isotypic component of 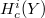 .
.
So we successfully "induce" a character of 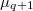 to obtain a (virtual) character of
to obtain a (virtual) character of 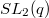 . It behaves much nicer than the naive induction from
. It behaves much nicer than the naive induction from 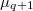 to
to 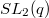 .
.
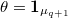 . Notice
. Notice ![$Y\rightarrow \mathbb{P}^1, (x,y)\mapsto [x:y]$](./latex/DeligneLusztig/latex2png-DeligneLusztig_141838292_-5.gif) gives an isomorphism
gives an isomorphism 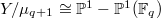 . So we have
. So we have ![$$H_c^*(Y)[\mathbf{1}]=H_c^*(Y/\mu_{q+1})=H_c^*(\mathbb{P}^1)-H_c^*(\mathbb{P}^1(\mathbb{F}_q))$$](./latex/DeligneLusztig/latex2png-DeligneLusztig_18991968_.gif) by excision.
by excision. 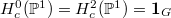 and
and 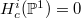 for
for 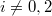 . So
. So 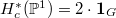 as a
as a 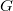 -representation.
-representation. 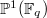 is simply a finite set of points, so
is simply a finite set of points, so ![$H_C^*(\mathbb{P}^1(\mathbb{F}_q))=H_c^0(\mathbb{P}^1(\mathbb{F}_q))=\overline{\mathbb{Q}}_\ell[\mathbb{P}^1(\mathbb{F}_q)]$](./latex/DeligneLusztig/latex2png-DeligneLusztig_57213920_-5.gif) and
and 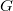 acts on it by permutation. This permutation action is the same as the left action of
acts on it by permutation. This permutation action is the same as the left action of 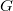 on
on 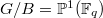 , hence
, hence ![$H_c^*(\mathbb{P}^1(\mathbb{F}_q))=\overline{\mathbb{Q}}_\ell[G/B]$](./latex/DeligneLusztig/latex2png-DeligneLusztig_2206267_-5.gif) , which is exactly
, which is exactly 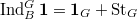 ! In particular,
! In particular, 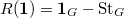 has degree
has degree 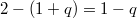 .
.
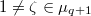 , then a fixed point formula of Deligne-Lusztig shows that
, then a fixed point formula of Deligne-Lusztig shows that 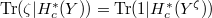 , whcih is zero since
, whcih is zero since 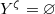 . Therefore the trace of any element
. Therefore the trace of any element 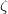 on
on 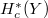 is zero if
is zero if 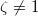 , hence as a
, hence as a 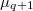 -virtual representation,
-virtual representation, 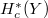 is a multiple of the regular representation
is a multiple of the regular representation ![$\overline{\mathbb{Q}}_\ell[\mu_{q+1}]$](./latex/DeligneLusztig/latex2png-DeligneLusztig_17925321_-5.gif) . In particular, every
. In particular, every 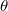 -isotypic component the same degree, which is
-isotypic component the same degree, which is 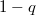 for
for 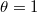 . Therefore
. Therefore 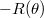 is a degree
is a degree  representation of
representation of 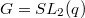 . It turns out to be irreducible when
. It turns out to be irreducible when 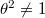 and is a direct sum of two representations of dimension
and is a direct sum of two representations of dimension 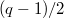 when
when 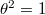 . These are exactly the discrete series representations of
. These are exactly the discrete series representations of 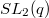 !
!
The discrete series representations have been realized in the cohomology of 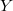 . Contemplating on this beautiful example, the following geometric picture emerges: the group
. Contemplating on this beautiful example, the following geometric picture emerges: the group 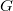 acts on
acts on 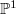 "horizontally" and
"horizontally" and 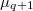 acts on
acts on 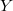 "vertically" by permuting the points in the fiber of
"vertically" by permuting the points in the fiber of 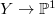 . One should really think of
. One should really think of 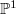 as the flag variety of
as the flag variety of 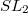 and
and 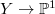 is a finite covering with the covering group the nonsplit torus
is a finite covering with the covering group the nonsplit torus 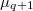 .
.
 Deligne-Lusztig varieties
Deligne-Lusztig varieties
We come back to the general consideration of finite groups of Lie type 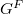 . Deligne and Lusztig generalized Drinfeld's construction to associate varieties to any such
. Deligne and Lusztig generalized Drinfeld's construction to associate varieties to any such 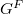 .
.
Let 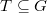 be a
be a 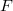 -stable maximal torus and
-stable maximal torus and 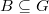 be a
be a 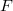 -stable Borel containing
-stable Borel containing 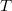 (their existence is ensured by Lang's theorem). Let
(their existence is ensured by Lang's theorem). Let 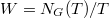 be the Weyl group. All Borel subgroups of
be the Weyl group. All Borel subgroups of 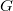 are conjugate: so the conjugate action of
are conjugate: so the conjugate action of 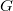 on the set of Borel subgroups of
on the set of Borel subgroups of 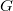 is transitive and the stabilizer the action of on
is transitive and the stabilizer the action of on 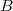 is simply
is simply 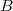 itself. Therefore we have a bijection
itself. Therefore we have a bijection 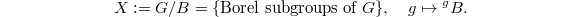 Now the Bruhat decomposition
Now the Bruhat decomposition 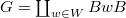 tells us that
tells us that 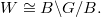 We say the two Borel subgroups
We say the two Borel subgroups 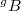 and
and 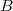 are in relative position
are in relative position 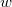 , where
, where 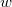 is the image of
is the image of 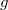 in
in 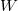 . The nice thing is that
. The nice thing is that 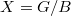 itself is a projective variety over
itself is a projective variety over 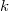 . We cut out a locally closed subvariety
. We cut out a locally closed subvariety 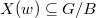 (Deligne-Lusztig variety) consisting of Borel subgroups
(Deligne-Lusztig variety) consisting of Borel subgroups 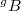 such that
such that 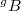 and
and 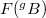 that are in relative position
that are in relative position 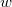 . In other words,
. In other words, 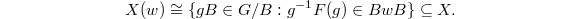 It is a smooth quasi-projective (indeed, quasi-affine, and conjecturally, affine) variety of dimension
It is a smooth quasi-projective (indeed, quasi-affine, and conjecturally, affine) variety of dimension 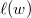 . This gives a stratification
. This gives a stratification 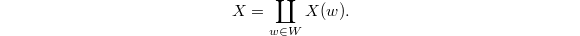 Notice the left action of
Notice the left action of 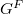 doesn't change the relative position, hence
doesn't change the relative position, hence 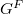 acts on each
acts on each 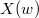 from the left, which is what we want.
from the left, which is what we want.
Let 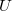 be the unipotent radical of
be the unipotent radical of 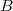 . Then
. Then 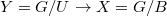 is a
is a 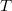 -torsor:
-torsor: 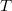 normalizes
normalizes 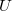 and acts on
and acts on 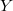 from the right. We define similarly a locally closed subvariety
from the right. We define similarly a locally closed subvariety 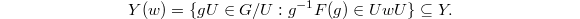 Then
Then 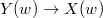 is indeed a
is indeed a 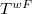 -torsor, where
-torsor, where 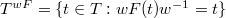 . Now we can play the same game by "inducing" a character
. Now we can play the same game by "inducing" a character 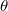 of the torus
of the torus 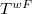 to obtain a virtual character
to obtain a virtual character 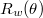 of
of 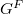 using the cohomology
using the cohomology 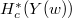 of the Deligne-Lusztig variety
of the Deligne-Lusztig variety 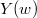 .
.
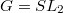 . Then the diagonal torus
. Then the diagonal torus 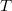 and the standard Borel are
and the standard Borel are 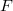 -stable. The Weyl group
-stable. The Weyl group 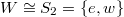 , with the nontrivial element
, with the nontrivial element 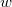 represented by
represented by 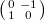 and maps the standard Borel to the opposite Borel, the subgroup of lower triangular matrices. The elements of
and maps the standard Borel to the opposite Borel, the subgroup of lower triangular matrices. The elements of 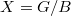 can be identified as complete flags
can be identified as complete flags 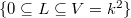 , in other words, points in
, in other words, points in 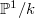 . Two flags are in relative position
. Two flags are in relative position 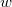 if and only if
if and only if 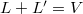 , in other words, two points in
, in other words, two points in 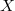 are in relative position
are in relative position 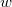 if and only they are distinct. In particular
if and only they are distinct. In particular 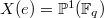 , and
, and 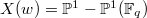 . An element in
. An element in 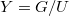 is nothing but a complete flag together with two vectors
is nothing but a complete flag together with two vectors 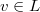 and
and 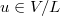 such that
such that 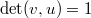 . Two marked flags are in relative position
. Two marked flags are in relative position 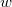 if and only if
if and only if 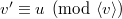 . Therefore
. Therefore 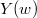 consists of marked flags such that
consists of marked flags such that 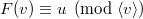 , i.e.,
, i.e., 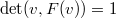 . Writing
. Writing 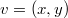 , this gives exactly
, this gives exactly 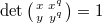 and recovers Drinfeld's ingenious construction. In this case
and recovers Drinfeld's ingenious construction. In this case 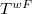 is exactly the nonsplit torus
is exactly the nonsplit torus 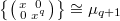 .
.
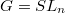 and
and 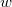 a permuatation of length
a permuatation of length 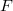 . One similarly obtains that
. One similarly obtains that 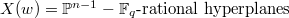 and
and 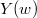 is given by the equation
is given by the equation 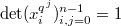 .
.
 ,
, 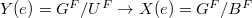 is a covering map between zero-dimensional varieties. Then
is a covering map between zero-dimensional varieties. Then 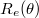 is simply the usual parabolic induction of a character
is simply the usual parabolic induction of a character 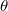 of
of 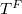 .
.
By carefully studying the geometry of the varieties 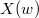 and
and 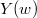 . Deligne-Lusztig proved:
. Deligne-Lusztig proved:
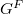 appears in
appears in 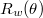 for some
for some 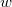 and
and 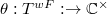 . Moreover,
. Moreover, 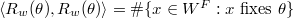 . In particular, when
. In particular, when 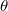 is in general position, i.e., no nontrivial elements of
is in general position, i.e., no nontrivial elements of 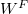 fixes
fixes 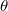 , one of
, one of 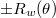 is an irreducible representation of
is an irreducible representation of 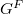 .
.
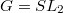 , the nontrivial element
, the nontrivial element 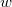 acts by
acts by 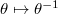 . The above theorem coincides with the fact that
. The above theorem coincides with the fact that 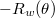 (discrete series) and
(discrete series) and 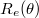 (principle series) is irreducible whenever
(principle series) is irreducible whenever 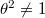 .
.
To complete the construction of all irreducible representations of any finite group of Lie type, it "suffices" to decompose each 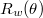 when
when 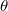 is not in general position. This task is far from trivial but was eventually done by Lusztig in 80's in a series of papers and books.
is not in general position. This task is far from trivial but was eventually done by Lusztig in 80's in a series of papers and books.
 Deligne-Lusztig curves
Deligne-Lusztig curves
Finally, let us consider the special case when dimension of 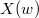 is one-dimensional. This corresponds to the case
is one-dimensional. This corresponds to the case 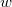 is a simple reflection. The relevant groups are groups of
is a simple reflection. The relevant groups are groups of 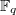 -rank 1. There are only four such groups:
-rank 1. There are only four such groups: 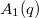 ,
, 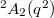 ,
, 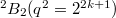 ,
, 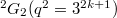 . Let
. Let 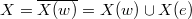 , then
, then 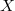 is a smooth projective curve over
is a smooth projective curve over 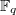 . One can compute the Euler characteristic of
. One can compute the Euler characteristic of 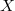 (hence the genus) and the number of rational points of
(hence the genus) and the number of rational points of 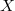 (=
(= 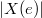 ) from the finite group data using the fixed point formula. We gather the results here (c.f., [7]).
) from the finite group data using the fixed point formula. We gather the results here (c.f., [7]).
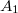 :
: 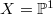 .
.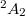 : The Fermat curve
: The Fermat curve 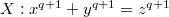 of degree
of degree 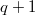 . It has genus
. It has genus 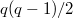 and
and 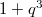
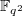 -points.
-points.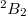 : The Deligne-Lusztig curve of Suzuki type (DLS). It has genus
: The Deligne-Lusztig curve of Suzuki type (DLS). It has genus 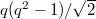 and
and 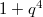
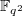 -points.
-points.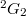 : The Deligne-Lusztig curve of Ree type (DLR). It has genus
: The Deligne-Lusztig curve of Ree type (DLR). It has genus 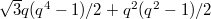 and
and 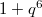
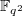 -points.
-points.
Now there comes no surprise that these curves admits a large number of automorphisms. A theorem of Stichtenoth asserts that 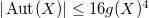 except
except 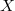 is Fermat curve
is Fermat curve 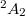 . A theorem of Henn shows that
. A theorem of Henn shows that 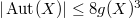 except the Fermat curve
except the Fermat curve 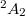 , the DLS, the hyperelliptic curve
, the DLS, the hyperelliptic curve 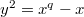 (
(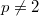 ) and the curve
) and the curve 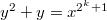 (
(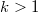 ,
, 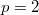 ). Amazingly enough you can go home and check by hand that the Deligne-Lusztig curves
). Amazingly enough you can go home and check by hand that the Deligne-Lusztig curves 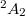 , DLS, DLR are all maximal curves: they all achieve the Hasse-Weil bound
, DLS, DLR are all maximal curves: they all achieve the Hasse-Weil bound 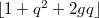 for the number of
for the number of 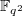 -rational points!
-rational points!
References
[1]Representations of reductive groups over finite fields, Ann. of Math. (2) 103 (1976), no.1, 103--161.
[2]Finite groups of Lie type, John Wiley \& Sons Inc., New York, 1985.
[3]Representations of finite groups of Lie type, Cambridge University Press, Cambridge, 1991.
[4]Representations of $\rm SL_2(\Bbb F_q)$, Springer-Verlag London Ltd., London, 2011.
[5]Modular representations of finite groups of Lie type, Cambridge University Press, Cambridge, 2006.
[6]A note on superspecial and maximal curves, Bull. Iranian Math. Soc 39 (2013), 405-413.
[7]Deligne-Lusztig varieties and group codes, Coding theory and algebraic geometry (Luminy, 1991), Lecture Notes in Math., 1518 Springer, 1992, 63--81.
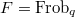 , we obtain
, we obtain 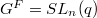 . The quotient by its center
. The quotient by its center 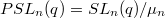 is simple except
is simple except 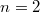 and
and 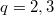 .
.