Given an elliptic curve 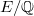 of analytic rank at most one, Kolyvagin proved that the Tate-Shafarevich group
of analytic rank at most one, Kolyvagin proved that the Tate-Shafarevich group 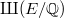 is finite using his theory of Euler systems. In the higher rank cases, Kolyvagin gave a conjectural description of the structure of the Selmer group in terms of the Euler system. This conjecture has recently been proved by Wei Zhang for a large class of elliptic curves. We shall explain Kolyvagin's conjecture, discuss some of its remarkable consequences and overview the strategy of the proof. To put things in context, we shall begin with a brief survey on the current status of the BSD conjecture.
is finite using his theory of Euler systems. In the higher rank cases, Kolyvagin gave a conjectural description of the structure of the Selmer group in terms of the Euler system. This conjecture has recently been proved by Wei Zhang for a large class of elliptic curves. We shall explain Kolyvagin's conjecture, discuss some of its remarkable consequences and overview the strategy of the proof. To put things in context, we shall begin with a brief survey on the current status of the BSD conjecture.
This is a note prepared for an Alcove Seminar talk at Harvard, Spring 2014. Our main references are [1] and [2].
 The BSD conjecture
The BSD conjecture
Let 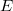 be an elliptic curve over a number field
be an elliptic curve over a number field 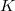 . Recall that the BSD conjecture relates the arithmetic invariants of
. Recall that the BSD conjecture relates the arithmetic invariants of 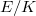 with the an analytic object, the
with the an analytic object, the 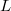 -function
-function 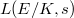 (see a lowbrow introduction).
(see a lowbrow introduction).
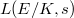 has analytic continuation over
has analytic continuation over 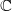 .
.- (Rank conjecture). Denote the analytic rank
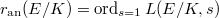 and the Mordell-Weil rank (or, algebraic rank)
and the Mordell-Weil rank (or, algebraic rank) 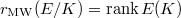 . Then
. Then 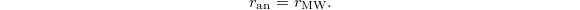
- (BSD formula) Denote
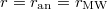 . Then
. Then
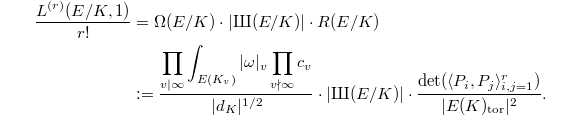 Here
Here  is the Neron differential of
is the Neron differential of 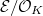 (see the remark),
(see the remark), ![$c_v=[\mathcal{E}(K_v):\mathcal{E}^0(K_v)]$](./latex/latex2png-KolyvaginConjecture_16310296_-5.gif) is the local Tamagawa number,
is the local Tamagawa number, 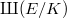 is the Tate-Shafarevich group,
is the Tate-Shafarevich group, 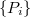 is a basis of the free part of
is a basis of the free part of 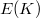 ,
, 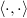 is the Neron-Tate height paring on
is the Neron-Tate height paring on 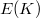 and
and 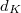 is the discriminant of
is the discriminant of 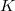 .
.
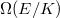 is called the period and
is called the period and 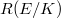 is called the regulator. Compare the BSD formula with classical class number formula
is called the regulator. Compare the BSD formula with classical class number formula 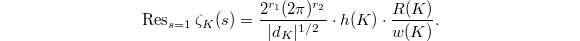
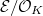 is a projective (but not necessarily free) module over
is a projective (but not necessarily free) module over 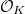 : so the global Neron differentials over
: so the global Neron differentials over 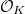 may not exists. A more elegant way to define the period is then to use adelic integration (with convergence factors). But since we will mainly talk about elliptic curves over
may not exists. A more elegant way to define the period is then to use adelic integration (with convergence factors). But since we will mainly talk about elliptic curves over 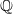 (and its base change over an imaginary quadratic field), we will not go into the details.
(and its base change over an imaginary quadratic field), we will not go into the details.
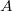 over number fields. The change in the BSD formula is to replace
over number fields. The change in the BSD formula is to replace 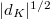 with
with 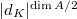 ,
, 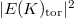 with
with 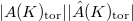 and the height pairing with
and the height pairing with 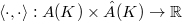 .
.
There has been vast progress on the BSD conjecture in recent years. We give a very brief (highly incomplete) summary.
Analytic continuation. Due to the recent work of someone in the audience, we now know 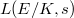 has analytic continuation for any totally real field
has analytic continuation for any totally real field 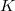 of degree
of degree 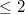 .
.
Rank. To make clear the rank part of the conjecture, we recall the 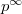 -descent exact sequence
-descent exact sequence ![$$0\rightarrow E(K) \otimes \mathbb{Q}_p/\mathbb{Z}_p\rightarrow\Sel_{p^\infty}(E/K)\rightarrow \Sha(E/K)[p^\infty]\rightarrow0. $$](./latex/latex2png-KolyvaginConjecture_95730982_.gif) The
The 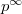 -Selmer group is a direct sum of several (denoted by
-Selmer group is a direct sum of several (denoted by 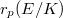 ) copies of
) copies of 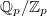 and a finite abelian
and a finite abelian  -group. Conjecturally,
-group. Conjecturally, ![$\Sha(E/K)[p^\infty]$](./latex/latex2png-KolyvaginConjecture_236883726_-5.gif) is finite, and hence conjecturally
is finite, and hence conjecturally 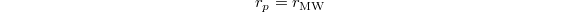 for any
for any  . Consider the following implications for
. Consider the following implications for 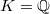 ,
, ![$$\xymatrix@R=2cm@C=0cm{& r_\mathrm{MW}=0, |\Sha[p^\infty]|<\infty \ar@{<=>}[ld]_{1)}& \\ r_p=0 \ar@{=>}[rr]^{3)} & & r_\mathrm{an}=0 \ar@{=>}[lu]_{2)}}.$$](./latex/latex2png-KolyvaginConjecture_191611989_.gif) The implication 1) is trivial. The implication 2) is due to Gross-Zagier and Kolyvagin (80s) for all
The implication 1) is trivial. The implication 2) is due to Gross-Zagier and Kolyvagin (80s) for all  . The implication 3) is due to Skinner-Urban (2000s) for
. The implication 3) is due to Skinner-Urban (2000s) for 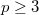 good ordinary with surjective mod
good ordinary with surjective mod  representation
representation ![$\bar\rho_{E,p}:G_\mathbb{Q}\rightarrow \Aut(E[p])$](./latex/latex2png-KolyvaginConjecture_74236986_-5.gif) . Now consider the analogous statement for rank 1 case,
. Now consider the analogous statement for rank 1 case, ![$$\xymatrix@R=2cm@C=0cm{& r_\mathrm{MW}=1, |\Sha[p^\infty]|<\infty \ar@{=>}[ld]_{1)}& \\ r_p=1 \ar@{=>}[rr]^{3)} & & r_\mathrm{an}=1 \ar@{=>}[lu]_{2)}}.$$](./latex/latex2png-KolyvaginConjecture_130584402_.gif) The implication 1) is trivial. The implication 2) is again due to Gross-Zagier and Kolyvagin. The implication 3) is due to Wei Zhang (2013) for
The implication 1) is trivial. The implication 2) is again due to Gross-Zagier and Kolyvagin. The implication 3) is due to Wei Zhang (2013) for 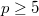 good ordinary with surjective
good ordinary with surjective 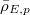 under some mild ramification hypothesis.
under some mild ramification hypothesis.
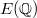 : together with Bhargava's counting method for 5-Selmer groups, Bhargava-Skinner-Zhang recently proved that at least 66% of all elliptic curves over
: together with Bhargava's counting method for 5-Selmer groups, Bhargava-Skinner-Zhang recently proved that at least 66% of all elliptic curves over 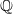 satisfy the rank part of the BSD conjecture!
satisfy the rank part of the BSD conjecture!
BSD formula. In the 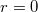 case, the
case, the  -part of the BSD formula is known for
-part of the BSD formula is known for 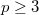 (under similar hypothesis) due to the work of Kato (2000s) and Skinner-Urban on the Iwasawa main conjecture for elliptic curves. In the
(under similar hypothesis) due to the work of Kato (2000s) and Skinner-Urban on the Iwasawa main conjecture for elliptic curves. In the 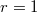 case, the
case, the  -part of the BSD formula is proved by Wei Zhang for
-part of the BSD formula is proved by Wei Zhang for 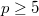 under similar hypothesis.
under similar hypothesis.
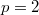 ! Unlike dealing with
! Unlike dealing with 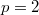 is not so popular in other fields of number theory, the
is not so popular in other fields of number theory, the 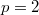 case is in fact extremely interesting: the major terms contributing the BSD formula indeed come from mysterious powers of 2 and 3. Also, since quadratic twists preserve the 2-torsion structure, understanding the 2-part of the BSD formula is important for understanding the arithmetic of elliptic curves in quadratic twist families (e.g., the congruent number curve family
case is in fact extremely interesting: the major terms contributing the BSD formula indeed come from mysterious powers of 2 and 3. Also, since quadratic twists preserve the 2-torsion structure, understanding the 2-part of the BSD formula is important for understanding the arithmetic of elliptic curves in quadratic twist families (e.g., the congruent number curve family 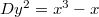 ). In practice, the 2-descent is the easiest to carry out and provides a useful computational tool.
). In practice, the 2-descent is the easiest to carry out and provides a useful computational tool.
 Kolyvagin's Euler system
Kolyvagin's Euler system
We now brief review the Euler system of Heegner points to motivate the statement of Kolyvagin's conjecture. In the next section, we shall state Wei Zhang's result on Kolyvagin's conjecture and deduce some of its consequences mentioned above.
Let 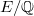 be an elliptic curve over
be an elliptic curve over 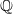 of conductor
of conductor 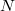 . Let
. Let 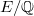 be an imaginary quadratic extension with discriminant
be an imaginary quadratic extension with discriminant 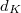 coprime to
coprime to 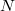 (we will assume
(we will assume 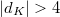 for simplicity). Let
for simplicity). Let 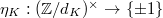 be the quadratic character associated to
be the quadratic character associated to 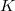 . We assume the Heegner condition: every prime factor of
. We assume the Heegner condition: every prime factor of 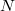 splits in
splits in 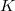 . Then
. Then 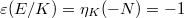 and the BSD conjecture predicts that
and the BSD conjecture predicts that 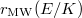 is odd (in particular,
is odd (in particular, 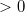 ). How do you construct a point?
). How do you construct a point?
The key thing is that under the Heegner condition, we have an abundant supply of algebraic points on 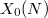 over the ring class fields of
over the ring class fields of 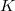 . Recall that
. Recall that 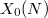 classifies cyclic
classifies cyclic 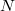 -isogenies between two elliptic curves
-isogenies between two elliptic curves 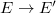 . For
. For 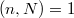 , let
, let 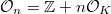 be the order of
be the order of 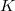 of conductor
of conductor 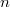 . Under the Heegner condition, there exists an ideal
. Under the Heegner condition, there exists an ideal 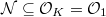 with norm
with norm  . Then we have a pair of elliptic curves with CM by
. Then we have a pair of elliptic curves with CM by  ,
,  with kernel
with kernel 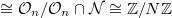 . This defines a point (a Heegner point)
. This defines a point (a Heegner point) 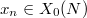 , which is defined over the ring class field
, which is defined over the ring class field 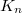 of
of 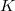 by the theory of complex multiplication. Here
by the theory of complex multiplication. Here 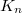 corresponds to the open compact subgroup
corresponds to the open compact subgroup 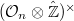 of
of 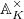 under class field theory (so
under class field theory (so 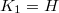 is the Hilbert class field of
is the Hilbert class field of 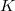 ). Using the modular parametrization
). Using the modular parametrization 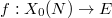 (mapping
(mapping 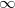 to 0) we obtain algebraic points
to 0) we obtain algebraic points 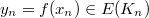 . Taking the trace using the group law on
. Taking the trace using the group law on 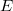 , we construct a Heegner point
, we construct a Heegner point 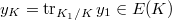 .
.
![$[\mathcal{O}_n]\in \Pic(\mathcal{O}_n)$](./latex/latex2png-KolyvaginConjecture_240087968_-5.gif) above, but any nontrivial class also works) and the choice of
above, but any nontrivial class also works) and the choice of 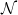 . Nevertheless it is well-defined up to sign and torsion, since the Atkin-Lehner involutions and
. Nevertheless it is well-defined up to sign and torsion, since the Atkin-Lehner involutions and 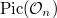 together act simply-transitively on all Heegner points;
together act simply-transitively on all Heegner points; ![$[\infty-0]$](./latex/latex2png-KolyvaginConjecture_175099459_-5.gif) is torsion on
is torsion on 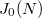 .
.
The big theorem of Gross-Zagier we went through last semester is the following.
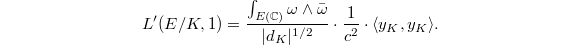 Here
Here  is the Manin constant defined so that
is the Manin constant defined so that 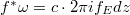 , here
, here 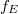 is the normalized eigenform associated to
is the normalized eigenform associated to 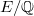 .
.
It follows from the Gross-Zagier formula that 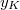 is infinite order if and only if
is infinite order if and only if 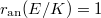 . When
. When 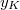 is of infinite order, Kolyvagin used his theory of Euler system to prove the finiteness of
is of infinite order, Kolyvagin used his theory of Euler system to prove the finiteness of 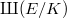 . A simple version of his theorem looks like
. A simple version of his theorem looks like
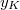 of infinite order. Let
of infinite order. Let 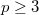 be prime such that
be prime such that 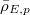 is surjective and
is surjective and 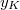 is not divisible by
is not divisible by  in
in 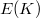 (this is true for almost all
(this is true for almost all  ). Then
). Then 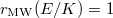 and
and ![$\Sha(E/K)[p]=0$](./latex/latex2png-KolyvaginConjecture_53814247_-5.gif) .
.
The rough idea of Kolyvagin's proof is that he constructed a system of cohomology classes in ![$H^1(K,E[p])$](./latex/latex2png-KolyvaginConjecture_202326559_-5.gif) derived from the Heegner points
derived from the Heegner points 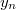 satisfying nice norm and congruence relations. The local information about these explicit cohomology classes were good enough to bound the Selmer group
satisfying nice norm and congruence relations. The local information about these explicit cohomology classes were good enough to bound the Selmer group 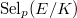 (via the local and global Tate duality and the Chebotarev density). More precisely, let
(via the local and global Tate duality and the Chebotarev density). More precisely, let 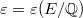 be the sign of the functional equation, then it was actually shown that
be the sign of the functional equation, then it was actually shown that 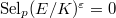 and
and 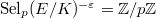 (the latter is contributed by
(the latter is contributed by 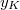 ).
).
We now briefly recall the construction of Kolyvagin's Euler system. The key thing is the following assumption:
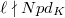 is inert in
is inert in 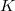 , and
, and 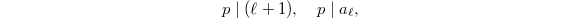 where
where 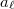 is the eigenvalue of the Hecke operator of
is the eigenvalue of the Hecke operator of 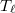 on the modular from
on the modular from 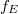 . Then we say
. Then we say  is a Kolyvagin prime. The positive integer
is a Kolyvagin prime. The positive integer 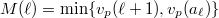 is called the Kolyvagin index.
is called the Kolyvagin index.
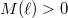 is equivalent to requiring
is equivalent to requiring 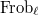 is in the conjugacy class of the complex conjugation in
is in the conjugacy class of the complex conjugation in ![$\Gal(\mathbb{Q}(E[p])/\mathbb{Q})$](./latex/latex2png-KolyvaginConjecture_173367636_-5.gif) . It follows from the Chebotarev density theorem that there is a positive density set of Kolyvagin primes.
. It follows from the Chebotarev density theorem that there is a positive density set of Kolyvagin primes.
The reason for this key condition is the following. Let 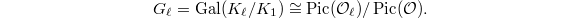 Since
Since  is inert in
is inert in 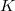 , we have
, we have 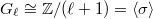 .
.
Then 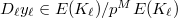 is indeed invariant under
is indeed invariant under 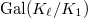 for
for 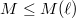 . To check this, we need to show that
. To check this, we need to show that 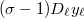 lies in
lies in 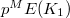 . Namely
. Namely 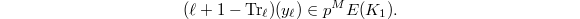 By assumption
By assumption 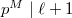 , so it remains to show that
, so it remains to show that 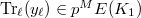 . This is true since by assumption
. This is true since by assumption 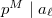 : the trace of the Heegner point
: the trace of the Heegner point 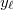 on
on 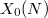 is exactly the Hecke operator
is exactly the Hecke operator 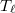 acting on
acting on 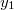 , which projects to
, which projects to 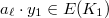 . The above relation is also the origin of the name Euler system:
. The above relation is also the origin of the name Euler system: 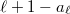 appears in the Euler factor of
appears in the Euler factor of 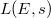 at
at  .
.
More generally,
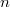 be a square-free product of Kolyvagin primes, then we say
be a square-free product of Kolyvagin primes, then we say 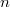 is a Kolyvagin number. The set of all Kolyvagin numbers is denoted by
is a Kolyvagin number. The set of all Kolyvagin numbers is denoted by 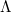 . We denote
. We denote 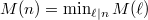 . Define
. Define ![$$D_n=\prod_{\ell\mid n}D_\ell\in \mathbb{Z}[G_n],$$](./latex/latex2png-KolyvaginConjecture_244540408_.gif) where
where 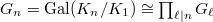 . Then
. Then ![$D_ny_n\in H^1(K_n,E[p^M])$](./latex/latex2png-KolyvaginConjecture_118950039_-5.gif) is indeed invariant under the Galois group
is indeed invariant under the Galois group 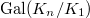 and descends to
and descends to ![$H^1(K_1, E[p^M])$](./latex/latex2png-KolyvaginConjecture_90349645_-5.gif) as long as
as long as 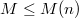 (because
(because =0$](./latex/latex2png-KolyvaginConjecture_188052400_-5.gif) ).
).
![$$c_M(n)=\sum_{s\in \Gal(K_1/K)}s D_ny_n\in H^1(K, E[p^M]),\quad M\le M(n).$$](./latex/latex2png-KolyvaginConjecture_56810074_.gif) The collection of cohomology classes
The collection of cohomology classes ![$$\kappa=\{c_M(n)\in H^1(K,E[p^M]): n\in \Lambda, M\le M(n)\}$$](./latex/latex2png-KolyvaginConjecture_5445769_.gif) is called a Kolyvagin system.
is called a Kolyvagin system.
 Kolyvagin's conjecture and consequences
Kolyvagin's conjecture and consequences
Notice 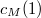 is nothing but the cohomology class of
is nothing but the cohomology class of  . In higher rank cases, the class
. In higher rank cases, the class 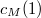 is indeed trivial by Gross-Zagier. Kolyvagin's Euler system constructs more classes
is indeed trivial by Gross-Zagier. Kolyvagin's Euler system constructs more classes 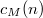 in
in ![$H^1(K,E[p^M])$](./latex/latex2png-KolyvaginConjecture_113869214_-5.gif) . One can ask whether some of these classes could be nontrivial. An obvious but crucial observation is that this is the same as asking whether some
. One can ask whether some of these classes could be nontrivial. An obvious but crucial observation is that this is the same as asking whether some 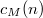 is not infinitely divisible by
is not infinitely divisible by  .
.
 , we define
, we define  to be the set of all Kolyvagin numbers with exactly
to be the set of all Kolyvagin numbers with exactly  prime factors. Define
prime factors. Define  to be the
to be the  -divisibility of the Kolyvagin cohomology classes
-divisibility of the Kolyvagin cohomology classes 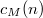 ,
, 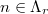 . Namely,
. Namely,  is the largest integer
is the largest integer  such that
such that 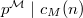 for all
for all 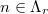 and
and 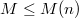 .
.
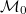 is simply the
is simply the  -divisibility of
-divisibility of 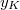 . In particular,
. In particular, 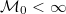 if and only if
if and only if 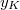 is of infinite order.
is of infinite order.
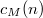 depending on
depending on  , the number of prime factors of
, the number of prime factors of 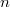 :
: 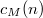 lies in the
lies in the 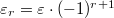 -eigenspace (e.g., when
-eigenspace (e.g., when 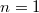 ,
, 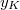 lies in the
lies in the 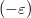 -eigenspace).
-eigenspace).
Kolyvagin proved that in fact 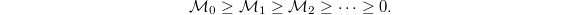 So increasing the number of prime factors of
So increasing the number of prime factors of 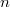 may help bring down the
may help bring down the  -divisibility! We define
-divisibility! We define 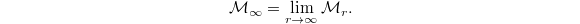
The hope is that even in the case that 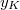 is torsion, the cohomology classes
is torsion, the cohomology classes 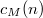 eventually becomes nontrivial.
eventually becomes nontrivial.
Assuming this key conjecture, Kolyvagin's work allows us to understand the refined structure of 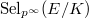 .
.
Starting from a nontrivial element by assumption 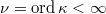 , Kolyvagin constructed the whole
, Kolyvagin constructed the whole 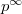 -Selmer group (even in the higher rank case!). Moreover, its
-Selmer group (even in the higher rank case!). Moreover, its 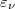 -eigenspace can be completely determined.
-eigenspace can be completely determined.
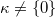 . Let
. Let 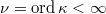 (so
(so 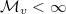 ).
).
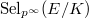 is contained in the subgroup of
is contained in the subgroup of ![$H^1(K,E[p^\infty])$](./latex/latex2png-KolyvaginConjecture_264287893_-5.gif) generated by
generated by 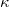 .
.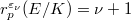 ;
; 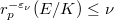 and has the same parity as
and has the same parity as  . Let
. Let 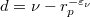 be the deficiency (so
be the deficiency (so 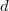 is even).
is even).- Let
![$\widetilde\Sha(E/K)[p^\infty]$](./latex/latex2png-KolyvaginConjecture_152864495_-5.gif) be the finite part of
be the finite part of 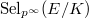 . Write
. Write ![$$\widetilde\Sha(E/K)[p^\infty]^{\varepsilon_\nu}=\left(\bigoplus_{i\ge1}\mathbb{Z}/p^{a_i}\right)^2,\quad \widetilde\Sha(E/K)[p^\infty]^{-\varepsilon_\nu}=\left(\bigoplus_{i\ge1} \mathbb{Z}/p^{b_i}\right)^2,$$](./latex/latex2png-KolyvaginConjecture_78399200_.gif) where
where 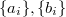 are non-increasing. Then
are non-increasing. Then 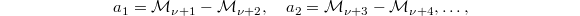 and
and 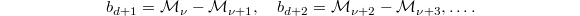 In particular,
In particular, 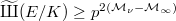 , with equality if and only if
, with equality if and only if 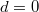 .
.
Now we are ready to state Wei Zhang's theorem precisely and then deduce some remarkable consequences.
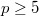 is good ordinary. Suppose
is good ordinary. Suppose 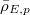 is surjective and ramifies at any
is surjective and ramifies at any 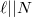 . Then
. Then 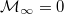 . In particular, Kolyvagin's conjecture is true.
. In particular, Kolyvagin's conjecture is true.
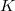 satisfying the Heegner hypothesis and
satisfying the Heegner hypothesis and 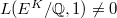 for the quadratic twist
for the quadratic twist 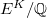 . Then by Gross-Zagier and Kolyvagin,
. Then by Gross-Zagier and Kolyvagin, 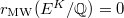 and
and 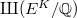 is finite. So
is finite. So 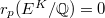 . Therefore
. Therefore 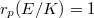 . Now by Kolyvagin's Theorem 3, b),
. Now by Kolyvagin's Theorem 3, b), 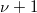 is equal to rank of the larger piece of
is equal to rank of the larger piece of 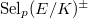 , which implies
, which implies 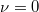 . So the desired result follows from Corollary 1.
¡õ
. So the desired result follows from Corollary 1.
¡õ
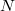 is square-free, one only needs to assume that
is square-free, one only needs to assume that 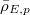 is ramified at any
is ramified at any 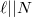 such that
such that 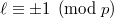 .
.
![$$\frac{\langle y_K,y_K\rangle}{[E(K): \mathbb{Z} y_K]^2}=\frac{\langle P,P\rangle}{|E(K)_\mathrm{tor}|^2},$$](./latex/latex2png-KolyvaginConjecture_42570804_.gif) comparing with the Gross-Zagier formula we know that the BSD formula for
comparing with the Gross-Zagier formula we know that the BSD formula for 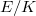 is equivalent to
is equivalent to ![$$\frac{1}{c^2}=\frac{\Sha(E/K)\prod_{v\nmid\infty} c_v}{[E(K):\mathbb{Z}y_K]^2}.$$](./latex/latex2png-KolyvaginConjecture_174901149_.gif) It is known in general that that the any prime factor of Manin constant
It is known in general that that the any prime factor of Manin constant  must divide
must divide 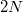 , so
, so  is coprime to
is coprime to  . Under the assumption
. Under the assumption 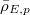 ramifies at
ramifies at 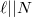 , each
, each 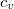 is coprime to
is coprime to  . So the
. So the  -part of the BSD formula is equivalent to
-part of the BSD formula is equivalent to ![$$\Sha(E/K)=[E(K): \mathbb{Z} y_K]^2$$](./latex/latex2png-KolyvaginConjecture_250209560_.gif) up to
up to  -adic units. By Theorem 3 c), this is equivalent to
-adic units. By Theorem 3 c), this is equivalent to 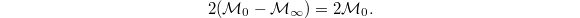 Namely,
Namely, 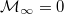 . This is exactly Theorem 4.
¡õ
. This is exactly Theorem 4.
¡õ
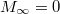 is precisely predicted by the BSD conjecture.
is precisely predicted by the BSD conjecture.
 Overview of the proof
Overview of the proof
Wei Zhang's proof beautifully blends various ideas and ingredients:
- "Deforming" the
 -Selmer group
-Selmer group 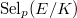 via congruences. For suitable level raising primes
via congruences. For suitable level raising primes 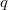 , Ribet and Diamond-Taylor's level raising theorems allow one to find a newform of level
, Ribet and Diamond-Taylor's level raising theorems allow one to find a newform of level 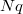 that is congruent to the original newform of level
that is congruent to the original newform of level 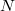 mod
mod  . In other words, one can keep the same
. In other words, one can keep the same ![$H^1(K, E[p])$](./latex/latex2png-KolyvaginConjecture_13086075_-5.gif) and vary the
and vary the  -Selmer groups while only changing one local condition at
-Selmer groups while only changing one local condition at 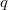 at a time.
at a time. - When the level raising prime
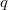 is chosen to be inert in
is chosen to be inert in 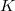 , the root number changes. Gross-Parson proves that the
, the root number changes. Gross-Parson proves that the  -Selmer parity changes as predicted (where the ramification assumption and
-Selmer parity changes as predicted (where the ramification assumption and 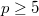 is needed). Together with the Chebotarev density argument, one is able to lower the
is needed). Together with the Chebotarev density argument, one is able to lower the  -Selmer rank via lever-raising. In the
-Selmer rank via lever-raising. In the 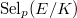 rank one case, Gross-Parson relates the level raising
rank one case, Gross-Parson relates the level raising  -Selmer rank
-Selmer rank 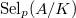 with the local
with the local  -divisibility of the generator of
-divisibility of the generator of 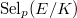 at
at 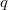 .
. - To actually show that
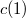 is the generator of
is the generator of 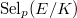 , one uses the Jochnowitz congruence, which relates the local
, one uses the Jochnowitz congruence, which relates the local  -divisibility of the Heegner point at
-divisibility of the Heegner point at 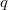 with the so-called algebraic part
with the so-called algebraic part 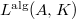 mod
mod  . To establish the Jochnowitz congruence, one needs the multiplicity one of the Hecke module of supersingular points on
. To establish the Jochnowitz congruence, one needs the multiplicity one of the Hecke module of supersingular points on 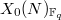 localized at a non-Eisenstein ideal, provided by Mazur's principle; and Gross's explicit Waldsburger formula on the definite quaternion algebra ramified at
localized at a non-Eisenstein ideal, provided by Mazur's principle; and Gross's explicit Waldsburger formula on the definite quaternion algebra ramified at 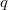 .
. - To compute
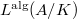 , one uses Skinner-Urban's BSD formula in the rank 0 case (where the good ordinary assumption is needed at the moment, but may be removed later). Showing
, one uses Skinner-Urban's BSD formula in the rank 0 case (where the good ordinary assumption is needed at the moment, but may be removed later). Showing 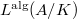 is nonzero mod
is nonzero mod  needs the comparison between the congruence ideal of
needs the comparison between the congruence ideal of 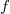 , the modular degree of
, the modular degree of 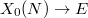 and the component group of the Neron model of
and the component group of the Neron model of 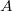 at
at 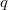 . This was established by Ribet and Takahashi.
. This was established by Ribet and Takahashi. - One then reduces the higher rank cases to the rank 1 case by successively lever-raising and rank lowering. To recover the nonvanishing of Kolyvagin's system from the rank one case, one uses a "triangularization" of
 -Selmer group and the following cohomological congruences between Heegner points: the localization at
-Selmer group and the following cohomological congruences between Heegner points: the localization at 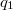 of
of 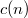 on
on 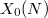 is congruent to the localization at
is congruent to the localization at 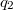 of
of 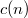 on the Shimura curve
on the Shimura curve 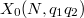 . This is a combination of Jochnowitz congruences and Bertolini-Darmon congruences (used in the their proof of the anti-cyclotomic Iwasawa main conjecture). The latter asserts that the localization at
. This is a combination of Jochnowitz congruences and Bertolini-Darmon congruences (used in the their proof of the anti-cyclotomic Iwasawa main conjecture). The latter asserts that the localization at 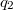 of Heegner points on
of Heegner points on 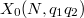 indeed factors through the component group at
indeed factors through the component group at 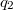 , hence can be linked to the reduction of Heegner points on the components of the Cerednik-Drinfeld fiber
, hence can be linked to the reduction of Heegner points on the components of the Cerednik-Drinfeld fiber 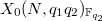 , which matches up with the Hecke module of supersingular points on the definite quaternion algebra ramified at
, which matches up with the Hecke module of supersingular points on the definite quaternion algebra ramified at 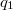 . The cohomological congruence is then established by the multiplicity one.
. The cohomological congruence is then established by the multiplicity one.
References
[1]Selmer groups and the divisibility of Heegner points, 2013, www.math.columbia.edu/~wzhang/math/online/Kconj.pdf.
[2]Kolyvagin's work on modular elliptic curves, $L$-functions and arithmetic (Durham, 1989), London Math. Soc. Lecture Note Ser., 153 Cambridge Univ. Press, Cambridge, 1991, 235--256.
![$D_\ell=\sum_{i=1}^\ell i\sigma^i\in \mathbb{Z}[G_\ell]$](./latex/latex2png-KolyvaginConjecture_45490191_-5.gif) which satisfies the key identity
which satisfies the key identity 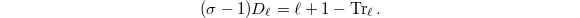
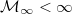 if and only if
if and only if 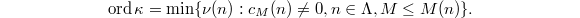 This is the smallest
This is the smallest 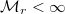 .
.
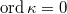 if and only if
if and only if 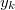 is of infinite order; Kolyvagin's conjecture is equivalent to
is of infinite order; Kolyvagin's conjecture is equivalent to 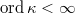 .
.
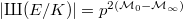 .
.
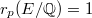 , then
, then 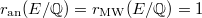 and
and 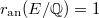 . Then the
. Then the