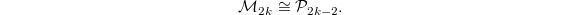We will describe a surprising phenomenon discovered by Zagier on values of quadratic polynomials. We will then provide an explanation using modular forms. Quadratic polynomials are quite simple objects everybody knew since childhood. Modular forms are less elementary but ubiquitous in modern number theory. In just one sentence, modular forms are special functions satisfying many symmetries. In particular they are periodic 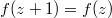 like the trigonometric function
like the trigonometric function 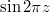 , and so a modular form has a Fourier expansion
, and so a modular form has a Fourier expansion 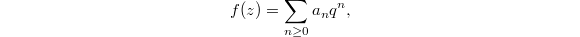 where
where 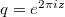 . The most famous example of a modular form is Ramanujan's
. The most famous example of a modular form is Ramanujan's 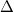 -function
-function 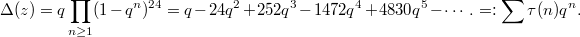 The coefficients
The coefficients 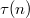 are of great arithmetic interest. If you never saw a modular form before, just remember the first few values of
are of great arithmetic interest. If you never saw a modular form before, just remember the first few values of 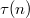 for the purpose of this talk.
for the purpose of this talk.
These are notes prepared for a talk for Columbia Undergraduate Math Society, Fall 2017. Most of the material is drawn from Zagier's beautiful paper [1] (tailored to fit a one-hour talk).
 Sums of values of quadratic polynomials
Sums of values of quadratic polynomials
Let 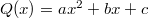 be a quadratic polynomial with
be a quadratic polynomial with 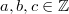 . Its discriminant
. Its discriminant 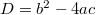 is a always congruent to 0 or 1 modulo 4, which is not a perfect square when
is a always congruent to 0 or 1 modulo 4, which is not a perfect square when 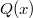 is irreducible. We will focus on the case
is irreducible. We will focus on the case 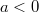 and
and 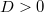 . So geometrically it corresponds to a cap-shape parabola intersecting with
. So geometrically it corresponds to a cap-shape parabola intersecting with  -axis at two points.
-axis at two points.
Let us consider the simplest case 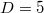 . Zagier came up with the following sum of values of quadratic polynomials with discriminant 5,
. Zagier came up with the following sum of values of quadratic polynomials with discriminant 5, 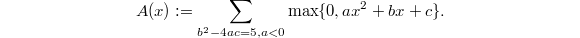 Here taking only positive values makes the sum more likely to converge. Assume there is no convergence issue for the moment. Notice that by construction
Here taking only positive values makes the sum more likely to converge. Assume there is no convergence issue for the moment. Notice that by construction 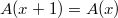 (as
(as 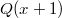 is also a polynomial with
is also a polynomial with 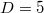 ) and
) and 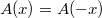 (change
(change 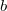 to
to 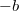 ). So
). So 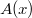 is an even and periodic function (of period 1). Can one make a wild guess what function this is?
is an even and periodic function (of period 1). Can one make a wild guess what function this is?
This is rather surprising. To convince you this is reasonable, let us compute 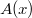 for some specific
for some specific  . Since
. Since 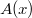 is even and periodic, we can focus on
is even and periodic, we can focus on 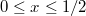 .
.
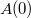 . Then
. Then 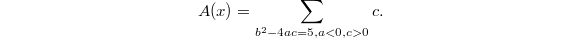 Notice
Notice 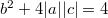 , so
, so 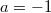 ,
, 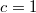 and
and 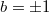 . Thus there are only two terms for the sum
. Thus there are only two terms for the sum  In particular,
In particular, 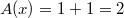 .
.
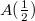 . Then
. Then 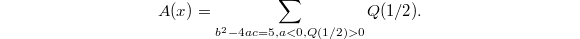 We use the identity
We use the identity 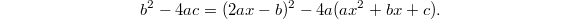 In particular, for
In particular, for 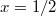 , we know
, we know 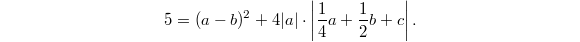 Since the last term is at least
Since the last term is at least 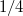 , we again obtain a bound on
, we again obtain a bound on 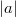 , and hence
, and hence 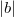 , and
, and 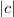 . It turns out we find four possible solutions
. It turns out we find four possible solutions 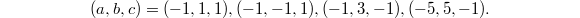 And so
And so 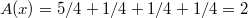 .
.
Now the same argument generalizes to any 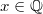 to show that the sum is in fact a finite sum. However, this sum can be infinite in general.
to show that the sum is in fact a finite sum. However, this sum can be infinite in general.
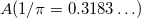 . Again the previous identity shows that
. Again the previous identity shows that 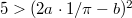 . So for any fixed
. So for any fixed  , we have a bound on
, we have a bound on 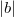 , and hence on
, and hence on 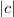 . This allows us to search for solution starting with small values of
. This allows us to search for solution starting with small values of 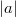 .
.
![\begin{center}
\begin{tabular}[h]{|c|c|}\hline
$(a,b,c)$ & $Q(1/\pi)$\\\hline
$(-1, 1, 1)$ & 1.217\\\hline
$(-1,1,1)$ & 0.580\\\hline
$(-5,5,-1)$ & 0.085\\\hline
$(-11, 7, -1)$ & 0.114\\\hline
$(-409, 259, -41)$ & 0.002 \\\hline
$(-541, 345, -55)$ & 0.002 \\\hline
\end{tabular}
\end{center}](./latex/ZagierQuadraticModular/latex2png-ZagierQuadraticModular_15127297_.gif) The convergence is indeed very fast: the first 6 terms already sum up to 2 (precision 1/1000). Of course
The convergence is indeed very fast: the first 6 terms already sum up to 2 (precision 1/1000). Of course 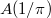 must be an infinite sum: if the sum is a finite sum and
must be an infinite sum: if the sum is a finite sum and 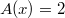 , then
, then  must satisfy a quadratic equation over
must satisfy a quadratic equation over 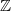 !
!
 Three variants
Three variants
Variant I. Of course there should be nothing special about 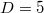 . One can do experiments for other
. One can do experiments for other 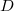 and one obtain similar pattern. Namely the function
and one obtain similar pattern. Namely the function 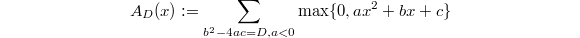 is always a constant function. Denoted this constant by
is always a constant function. Denoted this constant by 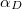 . Assuming
. Assuming 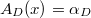 we can even figure out the value
we can even figure out the value 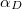 by computing
by computing 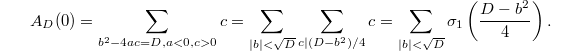 Here
Here 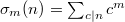 is the sum of divisor powers. The first few values of
is the sum of divisor powers. The first few values of  are:
are:
![\begin{center}
\begin{tabular}[h]{|c|c|c|c|c|c|}
$D$ & 5 & 8 & 12 & 13 & 17\\\hline
$\alpha_D$ & 2 & 5 & 10 & 10 & 20 \\
\end{tabular}
\end{center}](./latex/ZagierQuadraticModular/latex2png-ZagierQuadraticModular_229596720_.gif)
 : this sum can be recognized as the special value
: this sum can be recognized as the special value 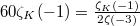 .
.
Variant II. Fix 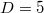 but let us change the sum using a higher power
but let us change the sum using a higher power 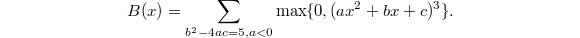 (Here we don't take an even power as it makes less sense to pick out the positive values, and the sum would diverge.) This is easier to prove to be converge (since
(Here we don't take an even power as it makes less sense to pick out the positive values, and the sum would diverge.) This is easier to prove to be converge (since 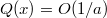 by the previous identity).
by the previous identity).
The surprise happens again.
Again there should be nothing special about 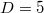 , in fact the function
, in fact the function 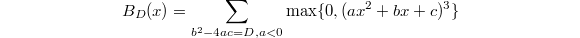 should be again a constant
should be again a constant 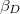 given by
given by 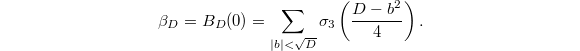 The first few values are given by
The first few values are given by
![\begin{center}
\begin{tabular}[h]{|c|c|c|c|c|c|}
$D$ & 5 & 8 & 12 & 13 & 17\\\hline
$\alpha_D$ & 2 & 11 & 46 & 58 & 164 \\
\end{tabular}
\end{center}](./latex/ZagierQuadraticModular/latex2png-ZagierQuadraticModular_186439060_.gif)
Variant III. Fix 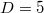 . Again there should be nothing special about 3rd powers. Let us consider the case of 5th powers
. Again there should be nothing special about 3rd powers. Let us consider the case of 5th powers 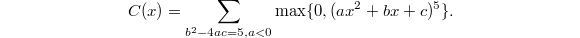 We would expect
We would expect 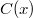 is again a constant function, given by the sum
is again a constant function, given by the sum 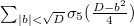 , which can be recognized as
, which can be recognized as 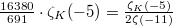 .
.
However, we get another surprise:
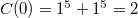 , while
, while 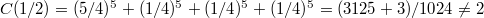 !
!
You probably already smell something like this, as it is impossible for a fixed collection of rational numbers to have all their 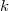 -th powers sum up to 2.
-th powers sum up to 2.
 The new phenomenon
The new phenomenon
Let us stare at the 5th power sum 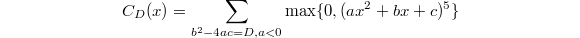 more carefully. Let us subtract the expected value
more carefully. Let us subtract the expected value 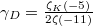 from the constant term,
from the constant term,
![\begin{center}
\renewcommand{\arraystretch}{1.5}
\begin{tabular}[h]{|c|c|c|}\hline
$D$ & 5 & 8\\\hline
$\gamma_D$ & $\frac{1742}{691}$ & $\frac{23465}{691}$\\\hline
$C_D(1/2)-\gamma_D$ & $\frac{47205}{88448}$ & $-\frac{47205}{44224}$ \\\hline
$C_D(1/3)-\gamma_D$ & $\frac{1175960}{4533651}$ & $-\frac{2351920}{4533651}$ \\\hline
$C_D(1/4)-\gamma_D$ & $-\frac{135855}{22642688}$ & $\frac{135855}{11321344}$ \\\hline
\end{tabular}
\end{center}](./latex/ZagierQuadraticModular/latex2png-ZagierQuadraticModular_58414580_.gif)
Notice the pattern: the second column is actually 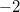 times the first column. More numerical data strongly suggest that
times the first column. More numerical data strongly suggest that 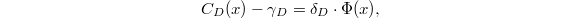 where
where 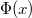 is independent of
is independent of 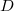 (the previous table shows
(the previous table shows 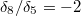 ). Moreover,
). Moreover, 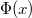 (of period 1) has average value 0. So its Fourier expansion has the form
(of period 1) has average value 0. So its Fourier expansion has the form 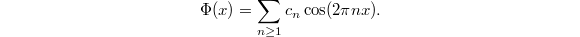 All these
All these 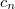 's are transcendental numbers, but the ratio
's are transcendental numbers, but the ratio 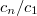 turns out to be very close to rational numbers numerically:
turns out to be very close to rational numbers numerically: 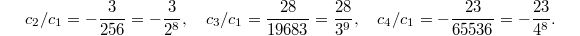 Now the miracle happens if we multiply
Now the miracle happens if we multiply 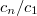 by
by 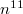 :
: 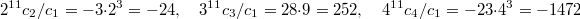 These are exactly Ramanujan's
These are exactly Ramanujan's  for
for 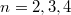 ! At the end we have produced the modular form
! At the end we have produced the modular form 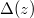 out of (the Fourier expansion of) the 5th power sum of values of quadratic polynomials!
out of (the Fourier expansion of) the 5th power sum of values of quadratic polynomials!
 What is going on?
What is going on?
As we have seen, the function 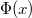 (normalized version of
(normalized version of 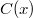 ) is closely related to Ramanujan's
) is closely related to Ramanujan's 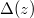 , a modular form for the group
, a modular form for the group 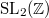 of weight 12. More precisely,
of weight 12. More precisely,
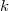 is a holomorphic function on the complex half-plan
is a holomorphic function on the complex half-plan 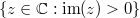 such that
such that 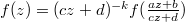 for all
for all 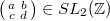 and holomorphic when
and holomorphic when 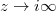 . Since
. Since 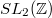 is generated by two elements
is generated by two elements 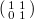 (translation) and
(translation) and 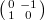 (inversion), this condition is equivalent to
(inversion), this condition is equivalent to 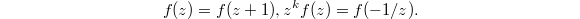 We say
We say 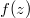 is a cusp form such that
is a cusp form such that 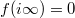 (equivalently the constant term
(equivalently the constant term 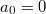 in its Fourier expansion). The space of modular forms (resp. cusp forms) of weight
in its Fourier expansion). The space of modular forms (resp. cusp forms) of weight 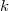 is usually denoted by
is usually denoted by 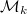 and
and 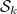 .
.
A fundamental theorem in the theory of modular forms is the space of modular forms of weight 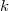 is finite dimensional. Its dimension can be easily computed.
is finite dimensional. Its dimension can be easily computed.
![\begin{center}
\begin{tabular}[h]{|c|c|c|c|c|c|c|c|c|c|}
$k$ & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18\\\hline
$\dim \mathcal{M}_k$ &0 & 1 & 1 & 1 & 1 & 2 & 1 & 2 & 2 \\
$\dim \mathcal{S}_k$ & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1
\end{tabular}
\end{center}](./latex/ZagierQuadraticModular/latex2png-ZagierQuadraticModular_98897830_.gif)
One can see weight 12 is the smallest weight for a cusp form to exist, which is exactly spanned by Ramanujan's 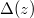 .
.
More generally, consider the function 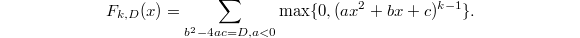 So
So 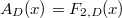 ,
, 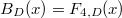 and
and 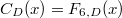 . Then the normalized version of
. Then the normalized version of 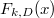 is closely related to the modular forms of level
is closely related to the modular forms of level 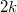 . The reason
. The reason 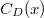 (or more generally
(or more generally 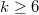 ) behaves differently from
) behaves differently from 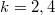 is exactly due to the fact that there are cusp forms of weight
is exactly due to the fact that there are cusp forms of weight 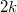 for
for 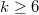 but not for
but not for 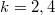 .
.
 The modular connection
The modular connection
To briefly explain the connection with modular forms, let us come back to the case of 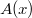 .
.
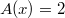 is to make the sum more symmetric:
is to make the sum more symmetric:
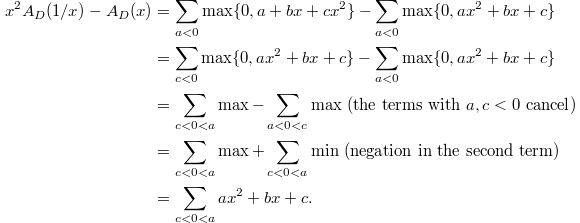 It is clearly that the last term sum to
It is clearly that the last term sum to 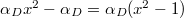 . This implies that the function
. This implies that the function 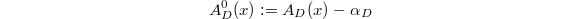 satisfies the functional equation
satisfies the functional equation 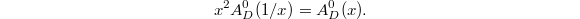 Using this together with the fact that
Using this together with the fact that 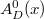 is even, period one, and
is even, period one, and 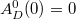 , and it follows that
, and it follows that 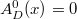 for any
for any 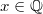 ! Then by a continuity argument we know
! Then by a continuity argument we know 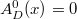 as desired.
as desired.
For more general 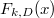 , we similarly consider
, we similarly consider 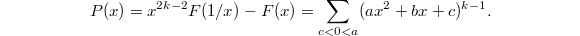 It is no longer obvious what the last sum is, but
It is no longer obvious what the last sum is, but 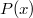 must satisfy the following functional equation (since
must satisfy the following functional equation (since 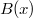 is even and has period 1):
is even and has period 1):
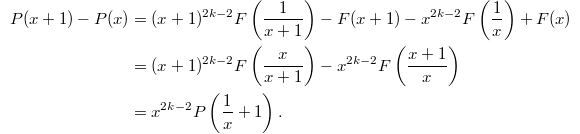
This is known as the space of period polynomials as they are related to period integrals of modular forms. One can produce polynomials in 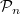 by period integrals of modular forms.
by period integrals of modular forms.
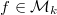 . We denote
. We denote 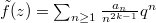 (the Eichler integral). Define
(the Eichler integral). Define 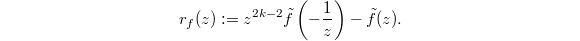 Then one can use the definition of modular forms to check that the
Then one can use the definition of modular forms to check that the 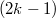 -st derivative of
-st derivative of 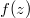 is 0, hence
is 0, hence 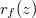 is a polynomial of degree
is a polynomial of degree 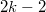 . We define
. We define 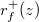 to be even degree part of
to be even degree part of 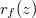 .
.
The fundamental theorem in the theory of modular forms is the following.
- When
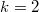 ,
, 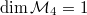 , so
, so 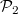 is 1-dimensional generated by
is 1-dimensional generated by 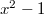 . As we have already seen this implies
. As we have already seen this implies 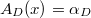 is a constant.
is a constant. - When
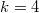 ,
, 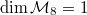 , so
, so 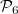 is again 1-dimensional, generated by
is again 1-dimensional, generated by 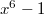 . The same argument as in the case
. The same argument as in the case 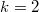 implies
implies 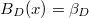 is again a constant.
is again a constant. - When
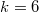 ,
, 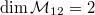 , and so there are two independent period polynomials in
, and so there are two independent period polynomials in  , which turns out to be
, which turns out to be 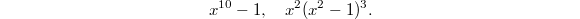 Let
Let 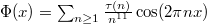 . Then
. Then 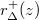 is given by (up to a transcendental period)
is given by (up to a transcendental period) 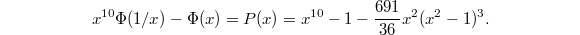 It is exactly the extra period polynomial causing
It is exactly the extra period polynomial causing 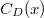 to be no longer a constant!
to be no longer a constant!
References
[1]From quadratic functions to modular functions, Number theory in progress, Vol. 2 (Zakopane-Ko\'scielisko, 1997), de Gruyter, Berlin, 1999, 1147--1178.
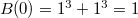 .
.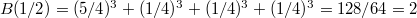 .
.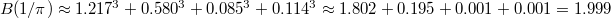 .
.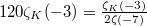 .
.
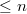 such that
such that 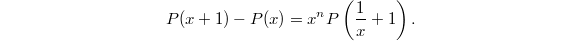
 induces is a canonical isomorphism
induces is a canonical isomorphism