Hilbert, in his 9th problem, posed the problem of finding the general reciprocity law for any number field. The class field theory developed in the first half of the 20th century was successful in answering this question for finite abelian extensions of 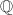 . As an easy consequence of class field theory, one can reproduce the classical Kronecker-Weber theorem, that is, every finite abelian extension of
. As an easy consequence of class field theory, one can reproduce the classical Kronecker-Weber theorem, that is, every finite abelian extension of 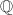 is a subfield of some cyclotomic extension
is a subfield of some cyclotomic extension 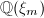 of
of 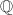 . Hilbert's 12th problem also asked how to extend the Kronecker-Weber theorem to an arbitrary ground number field, in other words, how to describe abelian extensions of a number field more explicitly.
. Hilbert's 12th problem also asked how to extend the Kronecker-Weber theorem to an arbitrary ground number field, in other words, how to describe abelian extensions of a number field more explicitly.
Motivated by the case of 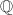 where all abelian extensions are obtained by adjoining the values of the exponential function, Kronecker conjectured, while he was studying elliptic functions, that all abelian extensions of an imaginary quadratic field should also arise in such a manner. This was achieved by the beautiful theory of complex multiplication, which allows one to describe all abelian extensions of an imaginary quadratic field via the values of the modular
where all abelian extensions are obtained by adjoining the values of the exponential function, Kronecker conjectured, while he was studying elliptic functions, that all abelian extensions of an imaginary quadratic field should also arise in such a manner. This was achieved by the beautiful theory of complex multiplication, which allows one to describe all abelian extensions of an imaginary quadratic field via the values of the modular 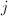 -function and the Weber function, or in the language of elliptic curves, via the
-function and the Weber function, or in the language of elliptic curves, via the 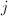 -invariant and (certain powers of)
-invariant and (certain powers of)  -coordinates of all torsion points of the corresponding elliptic curve. This problem for general number fields, known as Kronecker's Jugendtraum (dream of youth), is still largely open and is at the heart of current research in number theory.
-coordinates of all torsion points of the corresponding elliptic curve. This problem for general number fields, known as Kronecker's Jugendtraum (dream of youth), is still largely open and is at the heart of current research in number theory.
In this chapter, we will start by establishing the one-one correspondence between 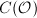 , the ideal class group of an order
, the ideal class group of an order  in an imaginary quadratic field
in an imaginary quadratic field  , and
, and 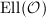 , the set of all isomorphism classes of elliptic curves with complex multiplication by
, the set of all isomorphism classes of elliptic curves with complex multiplication by  . Next, we will define the ring class field of
. Next, we will define the ring class field of  and then prove that it is obtained by adjoining the value
and then prove that it is obtained by adjoining the value 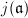 for any proper fractional ideal of
for any proper fractional ideal of  , using the method of reduction of elliptic curves. Moreover, the ray class fields of
, using the method of reduction of elliptic curves. Moreover, the ray class fields of  can be obtained by adjoining the values of the Weber function. Next, we will discuss the modular equation and use it to prove the integrality of
can be obtained by adjoining the values of the Weber function. Next, we will discuss the modular equation and use it to prove the integrality of 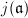 . The values of
. The values of 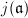 , i.e., the values of
, i.e., the values of 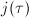 at the imaginary quadratic argument
at the imaginary quadratic argument  , are called singular moduli as they correspond to the
, are called singular moduli as they correspond to the 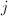 -invariants of singular elliptic curves. We will use Weber's method to explicitly compute singular moduli for orders of class number 1. These singular moduli turn out to be highly divisible as predicted by a remarkable theorem of Gross and Zagier. Gross and Zagier's theorem on singular moduli completely determines the prime factorization of the norm of the difference between two singular moduli. Our last section will be devoted to the algebraic proof of this theorem, relying on Deuring's results on the endomorphism rings of elliptic curves.
-invariants of singular elliptic curves. We will use Weber's method to explicitly compute singular moduli for orders of class number 1. These singular moduli turn out to be highly divisible as predicted by a remarkable theorem of Gross and Zagier. Gross and Zagier's theorem on singular moduli completely determines the prime factorization of the norm of the difference between two singular moduli. Our last section will be devoted to the algebraic proof of this theorem, relying on Deuring's results on the endomorphism rings of elliptic curves.
 Complex multiplication
Complex multiplication
As we saw in the first chapter, for a complex elliptic curve 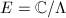 , the endomorphism ring
, the endomorphism ring 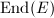 can be identified with
can be identified with 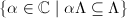 . When
. When  has complex multiplication,
has complex multiplication, 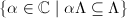 is an order
is an order  in an imaginary quadratic extension
in an imaginary quadratic extension  of
of 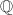 . Though complex conjugation will give us two isomorphisms between
. Though complex conjugation will give us two isomorphisms between  and
and 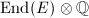 , we do have a canonical way to identify
, we do have a canonical way to identify  with
with 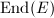 . Namely, for every
. Namely, for every 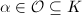 , we identify it with the endomorphism
, we identify it with the endomorphism ![$[\alpha]$](./latex/latex2png-MinorThesis3_68781034_-5.gif) of
of  induced by the multiplication
induced by the multiplication 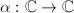 . In other words, the effect of
. In other words, the effect of ![$[\alpha]$](./latex/latex2png-MinorThesis3_68781034_-5.gif) on the invariant differential is given by
on the invariant differential is given by ![$[\alpha]^*\omega=\alpha\cdot\omega$](./latex/latex2png-MinorThesis3_191623990_-5.gif) . We call this identification the normalized identification.
. We call this identification the normalized identification.
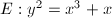 , then
, then 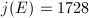 ,
, 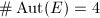 and
and  has complex multiplication by
has complex multiplication by ![$\mathbb{Z}[i]$](./latex/latex2png-MinorThesis3_42772926_-5.gif) . The normalized identification is given by the endomorphism
. The normalized identification is given by the endomorphism =(-x,iy)$](./latex/latex2png-MinorThesis3_140351950_-5.gif) , since
, since ![$[i]^*(dx/y)=d(-x)/(iy)=i(dx/y)$](./latex/latex2png-MinorThesis3_63969329_-5.gif) .
.
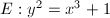 , then
, then 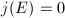 ,
, 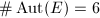 and
and  has complex multiplication by
has complex multiplication by ![$\mathbb{Z}[\rho]$](./latex/latex2png-MinorThesis3_49444867_-5.gif) , where
, where 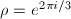 . The normalized identification is given by the endomorphism
. The normalized identification is given by the endomorphism =(\rho x,y)$](./latex/latex2png-MinorThesis3_99374539_-5.gif) , since
, since ![$[\rho]^*(dx/y)=d(\rho x)/y=\rho(dx/y)$](./latex/latex2png-MinorThesis3_148630286_-5.gif) .
.
Fix an order  in
in  . We are interested in studying all complex elliptic curves with endomorphism ring
. We are interested in studying all complex elliptic curves with endomorphism ring  . We denote the set of all these isomorphism classes by
. We denote the set of all these isomorphism classes by 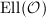 . As we will see in Theorem 1, it turns out that
. As we will see in Theorem 1, it turns out that 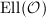 is in bijection with a purely algebraic object constructed from
is in bijection with a purely algebraic object constructed from  , namely the ideal class group of
, namely the ideal class group of  .
.
 and
and  be as above. Let
be as above. Let  be a fractional ideal of
be a fractional ideal of  , then
, then 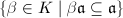 is a ring and contains the order
is a ring and contains the order  , so it is also an order. We say that
, so it is also an order. We say that  is proper if
is proper if 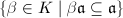 is equal to
is equal to  .
.
 , denoted by
, denoted by 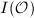 , forms a group ([1, 4.11]), called the ideal group of
, forms a group ([1, 4.11]), called the ideal group of  . Denote by
. Denote by 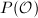 the subgroup of principal proper fractional ideals. The quotient group
the subgroup of principal proper fractional ideals. The quotient group 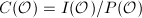 is called the ideal class group of
is called the ideal class group of  . When
. When  is the ring of integers
is the ring of integers 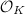 , we recover the ideal class group of
, we recover the ideal class group of  in the usual sense.
in the usual sense.
 is proper if and only if it is locally principal ([1, 5.4.2]), hence
is proper if and only if it is locally principal ([1, 5.4.2]), hence 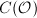 can be viewed as the reduced Grothendieck group
can be viewed as the reduced Grothendieck group 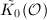 , i.e., the group of projective
, i.e., the group of projective  -modules of rank 1 ([2]).
-modules of rank 1 ([2]).
 be a complex elliptic curve with
be a complex elliptic curve with 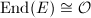 , then
, then 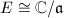 for some proper fractional ideal
for some proper fractional ideal  of
of  . Moreover,
. Moreover, 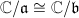 if and only
if and only  and
and 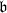 are in the same ideal class. Conversely, for every proper fractional ideal
are in the same ideal class. Conversely, for every proper fractional ideal  ,
, 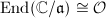 .
.
In other words, the above correspondence gives a bijection 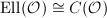 .
.
 is a complex elliptic curve, by Example 1 we know that
is a complex elliptic curve, by Example 1 we know that 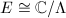 for some lattice
for some lattice 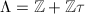 for some
for some 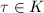 . We can view
. We can view 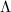 as a fractional ideal
as a fractional ideal  of
of  . Then, under the normalized identification,
. Then, under the normalized identification, 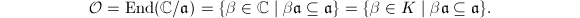 Therefore
Therefore  is a proper fractional ideal. Moreover,
is a proper fractional ideal. Moreover, 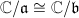 if and only if
if and only if 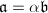 for some
for some 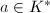 , if and only if
, if and only if  and
and 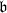 are in the same ideal class, since every principal fractional ideal is automatically proper.
are in the same ideal class, since every principal fractional ideal is automatically proper.
Conversely, suppose  is a proper fractional ideal, then
is a proper fractional ideal, then 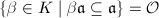 , hence
, hence 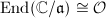 .
¡õ
.
¡õ
We will soon see that 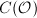 is a finite group. The order of
is a finite group. The order of 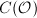 , denoted by
, denoted by 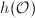 , is called the class number of
, is called the class number of  . So by Theorem 1, there are exactly
. So by Theorem 1, there are exactly 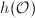 isomorphism classes of elliptic curves with complex multiplication by
isomorphism classes of elliptic curves with complex multiplication by  and each of them corresponds to an ideal class of
and each of them corresponds to an ideal class of  . Let
. Let  be an elliptic curve with
be an elliptic curve with 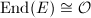 , then for any automorphism
, then for any automorphism 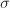 of
of 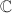 ,
, 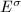 is also an elliptic curve with
is also an elliptic curve with 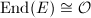 . So by the finiteness of the ideal class group and the above correspondence between
. So by the finiteness of the ideal class group and the above correspondence between 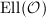 and
and 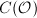 , we know
, we know 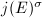 has finitely many values, hence
has finitely many values, hence 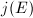 is an algebraic number of degree at most
is an algebraic number of degree at most 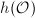 .
.
An amazing fact is that for an elliptic curve  with complex multiplication by
with complex multiplication by  ,
, 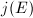 is actually an algebraic integer of degree
is actually an algebraic integer of degree 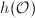 (Theorem 8). In particular, an elliptic curve with complex multiplication has a rational
(Theorem 8). In particular, an elliptic curve with complex multiplication has a rational 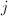 -invariant if and only
-invariant if and only 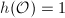 . We will calculate these
. We will calculate these 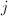 -invariants later.
-invariants later.
 Ring class fields
Ring class fields
Let  be an imaginary quadratic extension of
be an imaginary quadratic extension of 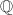 of discriminant
of discriminant 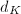 . The ring of integers
. The ring of integers 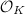 of
of  is equal to
is equal to 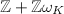 where
where 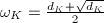 . Every order
. Every order  of
of  is a free
is a free 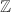 -module of rank 2, hence is of the form
-module of rank 2, hence is of the form  , where the positive integer
, where the positive integer 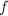 is called the conductor of
is called the conductor of  . When
. When 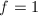 ,
, 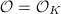 is the maximal order and is a Dedekind domain. But when
is the maximal order and is a Dedekind domain. But when 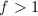 ,
,  is not integrally closed and hence is not a Dedekind domain. So it is not necessary for the unique factorization to hold for ideals in
is not integrally closed and hence is not a Dedekind domain. So it is not necessary for the unique factorization to hold for ideals in  . For example,
. For example, ![${\cal O}=\mathbb{Z}[\sqrt{-3}]$](./latex/latex2png-MinorThesis3_181885576_-5.gif) is an order of conductor 2 of
is an order of conductor 2 of 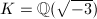 , and the ideal
, and the ideal 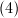 has two different prime factorizations
has two different prime factorizations 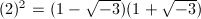 . However, we will see that the situation becomes better when we restrict our attention to the ideals prime to
. However, we will see that the situation becomes better when we restrict our attention to the ideals prime to  .
.
 prime to
prime to  is proper. An ideal
is proper. An ideal  of
of  is prime to
is prime to 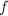 if and only if
if and only if 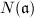 is prime to
is prime to 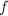 .
.
 is an ideal of
is an ideal of  prime to
prime to 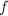 . By definition,
. By definition, 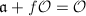 . Suppose
. Suppose 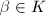 such that
such that 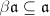 , then
, then 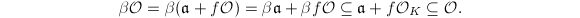 Hence
Hence 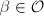 . It follows that
. It follows that  is proper.
is proper.
Next, let 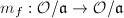 be multiplication by
be multiplication by 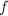 . Then
. Then 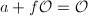 if and only if
if and only if 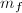 is surjective. But
is surjective. But 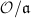 is an finite abelian group of order
is an finite abelian group of order 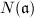 , so
, so 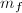 is surjective if and only if
is surjective if and only if 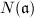 is prime to
is prime to 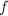 .
¡õ
.
¡õ
Therefore the ideals prime to 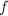 are in
are in 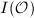 and are closed under multiplication. They generate a subgroup of fractional ideals
and are closed under multiplication. They generate a subgroup of fractional ideals 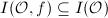 . Similarly define
. Similarly define 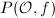 . Given any integer
. Given any integer  , every ideal class in
, every ideal class in 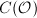 contains an ideal prime to
contains an ideal prime to  ([3, 7.17]). So the natural inclusion induces a surjective map
([3, 7.17]). So the natural inclusion induces a surjective map 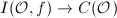 . Moreover, the kernel of this surjective map is
. Moreover, the kernel of this surjective map is 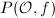 , so we have an isomorphism
, so we have an isomorphism 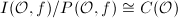 ([3, 7.19]).
([3, 7.19]).
Since 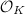 is a Dedekind domain, the first part of the next Proposition 2 ([3, 7.20, 7.22]) tells us that unique factorization does hold for fractional ideals of
is a Dedekind domain, the first part of the next Proposition 2 ([3, 7.20, 7.22]) tells us that unique factorization does hold for fractional ideals of  prime to
prime to 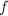 .
.
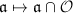 induces an isomorphism
induces an isomorphism 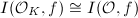 , and the inverse map is given by
, and the inverse map is given by 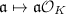 . The isomorphism
. The isomorphism 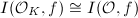 induces an isomorphism
induces an isomorphism 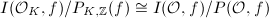 , where
, where 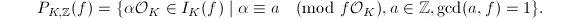
Viewing 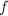 as a cycle of
as a cycle of  , we know that
, we know that 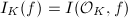 and that
and that 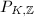 is a subgroup of
is a subgroup of 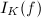 containing
containing 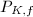 (we use the symbols for generalized ideal groups as in [4, VI]). Hence, by class field theory,
(we use the symbols for generalized ideal groups as in [4, VI]). Hence, by class field theory, 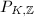 corresponds to a finite abelian extension
corresponds to a finite abelian extension 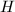 of
of  .
.
Combining the isomorphism 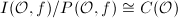 and the second part of Proposition 2, we know that
and the second part of Proposition 2, we know that 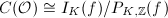 , and composing with the Artin map we obtain an isomorphism
, and composing with the Artin map we obtain an isomorphism 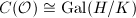 . In particular,
. In particular, 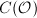 is a finite group. Again, when
is a finite group. Again, when 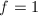 , i.e.,
, i.e.,  is the maximal order
is the maximal order 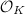 , the ring class field of
, the ring class field of  is just the usual Hilbert class field of
is just the usual Hilbert class field of  . So we may regard the ring class field as a generalization of the Hilbert class field.
. So we may regard the ring class field as a generalization of the Hilbert class field.
![$\mathbb{Z}[-\sqrt{n}]$](./latex/latex2png-MinorThesis3_136031181_-5.gif) is related to the classical problem of determining the primes of the form
is related to the classical problem of determining the primes of the form 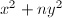 studied by Fermat, Euler, Lagrange, Legendre and Gauss. More precisely, let
studied by Fermat, Euler, Lagrange, Legendre and Gauss. More precisely, let  be a real algebraic integer such that the ring class field
be a real algebraic integer such that the ring class field  and let
and let  be its minimal polynomial, then for odd
be its minimal polynomial, then for odd  dividing neither
dividing neither  nor the discriminant of
nor the discriminant of 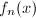 , we have
, we have 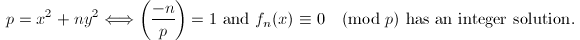 See [3] for this beautiful story.
See [3] for this beautiful story.
 Main theorems of complex multiplication
Main theorems of complex multiplication
The first main result of this section is the ``First Main Theorem'' of complex multiplication, which says the ring class field of  can be obtained by adjoining the value of
can be obtained by adjoining the value of 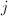 -function at any proper ideal of
-function at any proper ideal of  . The key step of the proof is to establish the so-called Hasse congruence (Theorem 2), which expresses the Frobenius action on the value of the
. The key step of the proof is to establish the so-called Hasse congruence (Theorem 2), which expresses the Frobenius action on the value of the 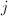 -function via the action on the argument of the
-function via the action on the argument of the 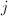 -function. There are several different approaches to do so: the complex analytic method using the modular equation, or the algebraic method we choose here using the reduction of elliptic curves. We follow mainly the exposition of [5] and [3].
-function. There are several different approaches to do so: the complex analytic method using the modular equation, or the algebraic method we choose here using the reduction of elliptic curves. We follow mainly the exposition of [5] and [3].
First, by using Chebotarev's density theorem, one can show the following characterization of field extensions by the primes which split completely ([3, 8.20]). We will utilize this Lemma 1 twice to characterize the ring class field in Lemma 2.
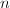 be a number field. Let
be a number field. Let 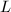 be a finite Galois extension of
be a finite Galois extension of 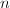 and
and 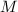 be a finite extension of
be a finite extension of 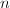 . Then
. Then 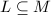 if and only if for all but finitely many unramified primes
if and only if for all but finitely many unramified primes 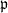 of
of 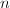 which have a degree 1 prime
which have a degree 1 prime 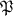 of
of 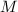 above
above 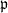 ,
, 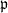 splits completely in
splits completely in 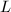 .
.
From now on, let us fix an order  of conductor
of conductor 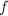 in an imaginary quadratic field
in an imaginary quadratic field  . Let
. Let 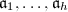 (
(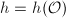 ) be the representatives of the ideal class group
) be the representatives of the ideal class group 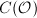 and
and 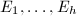 be the corresponding elliptic curves with complex multiplication by
be the corresponding elliptic curves with complex multiplication by  via Theorem 1. Let
via Theorem 1. Let 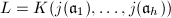 .
.
 be a prime which splits as
be a prime which splits as 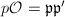 . If for all but finitely many such
. If for all but finitely many such  , we have the congruence
, we have the congruence 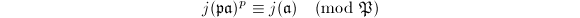 for any proper fractional ideal
for any proper fractional ideal  of
of  and any prime
and any prime 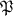 of
of 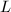 over
over  , then
, then 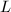 is the ring class field of
is the ring class field of  for any proper fractional ideal
for any proper fractional ideal  of
of  .
.
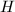 be the ring class field of
be the ring class field of  . Let us first show that
. Let us first show that 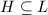 . Suppose
. Suppose  is a unramified prime of
is a unramified prime of 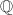 and
and 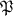 is a degree 1 prime of
is a degree 1 prime of 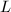 over
over  . By Lemma 1, it suffices to show that for all but finitely many such
. By Lemma 1, it suffices to show that for all but finitely many such  ,
,  splits completely in
splits completely in 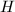 . Since
. Since 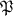 is of degree 1, we already know that
is of degree 1, we already know that  must split completely as
must split completely as 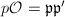 in
in  for some primes
for some primes 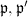 of
of  . By the assumption, for all but finitely many such
. By the assumption, for all but finitely many such  , we have
, we have 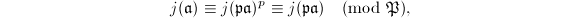 where the second equality is because
where the second equality is because 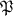 has degree 1. Excluding the finitely many primes
has degree 1. Excluding the finitely many primes  such that
such that 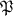 divides any of the differences
divides any of the differences 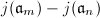 , we conclude that
, we conclude that 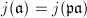 for all but finitely many primes
for all but finitely many primes  . So
. So 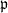 is a principal ideal of
is a principal ideal of  and hence has trivial Artin symbol, therefore
and hence has trivial Artin symbol, therefore  splits completely in
splits completely in 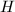 .
.
Next let us show that 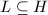 . Let
. Let 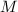 be the Galois closure of
be the Galois closure of 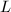 . Suppose
. Suppose  is a prime which splits completely in
is a prime which splits completely in 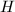 . Again by Lemma 1, it suffices to show that for all but finitely such
. Again by Lemma 1, it suffices to show that for all but finitely such  ,
,  splits completely in
splits completely in 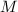 . Since
. Since  splits completely in
splits completely in 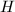 ,
, 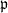 must be a principal ideal of
must be a principal ideal of  and then
and then 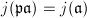 . So by assumption,
. So by assumption, 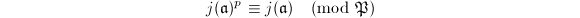 for all but finitely many such
for all but finitely many such  and any prime
and any prime 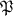 of
of 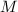 above
above  . Now suppose further that
. Now suppose further that  does not divide the index
does not divide the index ![$[{\cal O}_L:{\cal O}_K(j(\mathfrak{a}))]$](./latex/latex2png-MinorThesis3_72240984_-5.gif) , then we have
, then we have 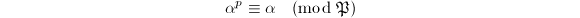 for any
for any 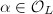 , hence
, hence 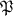 has degree 1 for any
has degree 1 for any 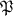 above
above  . Therefore
. Therefore  splits completely in
splits completely in 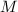 .
¡õ
.
¡õ
 be a prime satisfying that
be a prime satisfying that 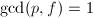 ,
,  splits as
splits as 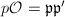 and the
and the 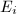 's have good reduction at
's have good reduction at  . Then for any proper fractional ideal
. Then for any proper fractional ideal  of
of  and any prime
and any prime 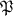 of
of 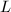 above
above  , we have the Hasse congruence
, we have the Hasse congruence 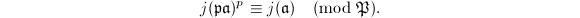
 ,
, 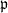 and
and 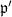 are proper. We may assume that
are proper. We may assume that 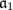 and
and 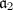 represent
represent  and
and 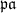 in the ideal classes. Then
in the ideal classes. Then 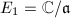 ,
, 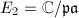 and we have a natural isogeny
and we have a natural isogeny 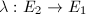 since
since 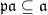 . Because
. Because  splits completely, we know that
splits completely, we know that 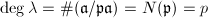 . Now find an ideal
. Now find an ideal 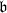 prime to
prime to  in the ideal class of
in the ideal class of 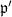 , then
, then 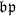 is a principal ideal generated by some
is a principal ideal generated by some 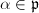 . Therefore
. Therefore 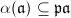 induces an isogeny
induces an isogeny 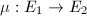 and
and 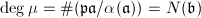 is prime to
is prime to  by our choice of
by our choice of 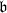 . The composition
. The composition 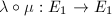 is given by
is given by 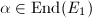 via the normalized identification of
via the normalized identification of  and
and 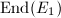 .
.
Now since the 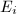 's have good reduction at
's have good reduction at  , reducing modulo
, reducing modulo 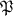 we get an isogeny
we get an isogeny 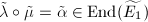 . But
. But 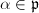 , so
, so 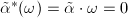 where
where 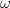 is the invariant differential of
is the invariant differential of 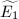 . Therefore
. Therefore 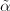 is inseparable. As the reduction does not change the degree of an isogeny,
is inseparable. As the reduction does not change the degree of an isogeny, 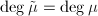 is prime to
is prime to  , hence
, hence 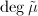 is separable. We conclude that
is separable. We conclude that 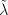 is inseparable. But
is inseparable. But 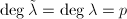 , hence
, hence 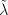 is purely inseparable. So
is purely inseparable. So 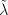 is the composition of the
is the composition of the  -Frobenius
-Frobenius 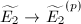 and an isomorphism
and an isomorphism 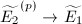 . Hence
. Hence 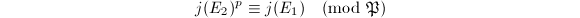 and the claim follows.
¡õ
and the claim follows.
¡õ
From Theorem 2 and Lemma 2, we already know that 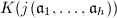 is actually the ring class field
is actually the ring class field 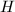 of
of  . Further more, we can use the limited information of the Hasse congruence to compute the Galois action on the
. Further more, we can use the limited information of the Hasse congruence to compute the Galois action on the 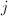 -values.
-values.
 of
of  and
and 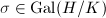 , we have
, we have 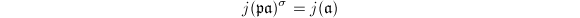 for any proper ideal
for any proper ideal 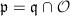 , where
, where 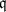 is a prime of
is a prime of  whose Artin symbol is
whose Artin symbol is 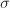 . In particular,
. In particular, 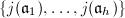 is the Galois orbit of
is the Galois orbit of 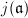 for any proper fractional ideal
for any proper fractional ideal  of
of  and
and ![$[\mathbb{Q}(j(\mathfrak{a})):\mathbb{Q}]=[K(j(\mathfrak{a})):K]=h$](./latex/latex2png-MinorThesis3_141025169_-5.gif) , where
, where 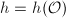 .
.
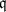 of
of  whose Artin symbol is
whose Artin symbol is  . By Theorem 2, for all but finitely many such primes
. By Theorem 2, for all but finitely many such primes  (excluding those not prime to
(excluding those not prime to 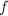 ), we have
), we have 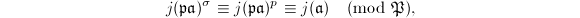 where
where 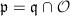 is proper and
is proper and 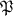 is any prime of
is any prime of 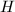 over
over  . Since these
. Since these 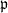 's have the same Artin symbol, they must lie in the same ideal class of
's have the same Artin symbol, they must lie in the same ideal class of  . So
. So 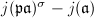 is the same for every
is the same for every 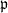 and has infinitely many prime factors, therefore it must be zero. We conclude that
and has infinitely many prime factors, therefore it must be zero. We conclude that 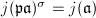 . The remaining part follows since
. The remaining part follows since ![$[K:\mathbb{Q}]\le2$](./latex/latex2png-MinorThesis3_169673901_-5.gif) and we already know
and we already know ![$[\mathbb{Q}(j(\mathfrak{a})):\mathbb{Q}]\le h$](./latex/latex2png-MinorThesis3_232645048_-5.gif) .
¡õ
.
¡õ
Now we are in a position to prove the First Main Theorem of complex multiplication.
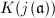 is the ring class field of
is the ring class field of  for any proper fractional ideal
for any proper fractional ideal  of
of  . In particular,
. In particular, 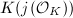 is the Hilbert class field of
is the Hilbert class field of  .
.
As a consequence of the First Main Theorem 4, all everywhere unramified extensions of  can be obtained as a subfield of
can be obtained as a subfield of 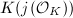 . Moreover, one can show that an abelian extension of
. Moreover, one can show that an abelian extension of  is generalized dihedral over
is generalized dihedral over  if and only if it is contained in the ring class field of some order in
if and only if it is contained in the ring class field of some order in  ([3, 9.18]), so the First Main Theorem also tells us how to construct generalized dihedral extensions explicitly. Now, it is natural to ask how to generate all abelian extensions of
([3, 9.18]), so the First Main Theorem also tells us how to construct generalized dihedral extensions explicitly. Now, it is natural to ask how to generate all abelian extensions of  , in other words, how to give an explicit description of the ray class fields of
, in other words, how to give an explicit description of the ray class fields of  . This is the content of the ``Second Main Theorem'' of complex multiplication.
. This is the content of the ``Second Main Theorem'' of complex multiplication.
 be an elliptic curve with a Weierstrass model
be an elliptic curve with a Weierstrass model 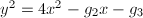 . For any
. For any 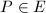 , define the Weber function
, define the Weber function
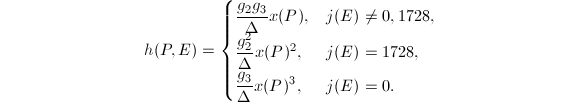 So the Weber function is essentially the
So the Weber function is essentially the  -coordinate function on the elliptic curve
-coordinate function on the elliptic curve  . Notice that the powers of the coordinate
. Notice that the powers of the coordinate 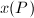 and the normalized constants appearing in the expression are chosen in the way that
and the normalized constants appearing in the expression are chosen in the way that 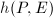 is invariant under the isomorphisms of elliptic curves. In the language of lattices, we may define the Weber function
is invariant under the isomorphisms of elliptic curves. In the language of lattices, we may define the Weber function 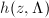 as follows:
as follows:
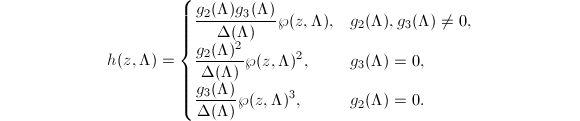
Now let us establish an analog of the Hasse congruence for the Weber function.
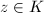 and
and 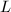 be an extension of
be an extension of  containing all
containing all 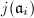 's and
's and 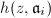 's. Let
's. Let  be a prime satisfying
be a prime satisfying 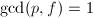 ,
,  splits as
splits as 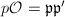 and
and 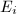 's have good reduction at
's have good reduction at  . Then for any proper fractional ideal
. Then for any proper fractional ideal  of
of  and any prime
and any prime 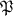 of
of 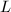 above
above  , we have the congruence
, we have the congruence 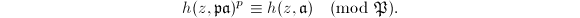
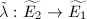 which is the composition of the
which is the composition of the  -Frobenius
-Frobenius 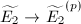 and an isomorphism
and an isomorphism 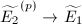 . Since the Weber function is invariant under isomorphisms, we know that
. Since the Weber function is invariant under isomorphisms, we know that 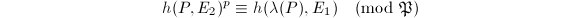 and the claim follows since
and the claim follows since 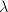 is just the natural projection.
¡õ
is just the natural projection.
¡õ
After the congruence in Theorem 5 is established, a similar argument as for ring class fields will allow us to construct all the ray class fields of  . We state this Second Main Theorem and omit the details of the proof here. Roughly speaking, the maximal abelian extension of
. We state this Second Main Theorem and omit the details of the proof here. Roughly speaking, the maximal abelian extension of  is generated by
is generated by  and the
and the  -coordinates of all torsion points of the corresponding elliptic curve with complex multiplication by
-coordinates of all torsion points of the corresponding elliptic curve with complex multiplication by 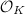 . See [3, 11.39] and [6, II.5] for more.
. See [3, 11.39] and [6, II.5] for more.
 be an ideal of
be an ideal of 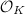 and
and  be an elliptic curve with complex multiplication by
be an elliptic curve with complex multiplication by 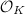 . Let
. Let ![$E[\mathfrak{a}]=\{P\in E\mid [\alpha]P=O, \alpha\in \mathfrak{a}\}$](./latex/latex2png-MinorThesis3_209562922_-5.gif) be the
be the  -torsion points of
-torsion points of  , then
, then ![$K(j(E), h(E[\mathfrak{a}],E))$](./latex/latex2png-MinorThesis3_90976662_-5.gif) is the ray class field of
is the ray class field of  with respect to the cycle
with respect to the cycle  . In particular, the maximal abelian extension of
. In particular, the maximal abelian extension of  is equal to
is equal to 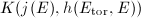 .
.
 Modular equations and the integrality of singular moduli
Modular equations and the integrality of singular moduli
We have seen that 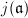 is an algebraic number of degree
is an algebraic number of degree 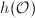 from Theorem 3. But in fact more is true: it is an algebraic integer. There are several possible proofs of this fact: the complex analytic proof using the modular equation, the good reduction proof due to Serre and Tate, and the bad reduction proof due to Serre ([6, II.6]). We have not talked much about the analytic aspect of
from Theorem 3. But in fact more is true: it is an algebraic integer. There are several possible proofs of this fact: the complex analytic proof using the modular equation, the good reduction proof due to Serre and Tate, and the bad reduction proof due to Serre ([6, II.6]). We have not talked much about the analytic aspect of 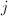 -function so far, so we will choose the first approach here.
-function so far, so we will choose the first approach here.
Let us first recall some facts about the modular curve 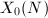 , which plays an important role in modern number theory. The modular curve
, which plays an important role in modern number theory. The modular curve 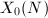 is a compact Riemann surface constructed by compactifying
is a compact Riemann surface constructed by compactifying 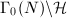 , the quotient of upper half plane by the congruence group
, the quotient of upper half plane by the congruence group 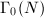 . It is the compactification of the moduli space of elliptic curves along with the level structure of a cyclic subgroup of order
. It is the compactification of the moduli space of elliptic curves along with the level structure of a cyclic subgroup of order 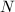 . Viewing
. Viewing 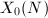 as a complex algebraic curve, the function field of
as a complex algebraic curve, the function field of 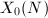 is equal to
is equal to 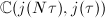 . So
. So 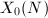 has a planar model defined by some complex polynomial
has a planar model defined by some complex polynomial 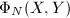 satisfying
satisfying 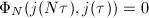 , called the modular equation of level
, called the modular equation of level 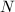 ([7]).
([7]).
An unexpected result is that the modular equation 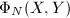 in fact has rational, or even better, integer coefficients. Therefore,
in fact has rational, or even better, integer coefficients. Therefore, 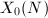 can be defined as an algebraic curve over
can be defined as an algebraic curve over 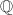 without reference to the complex numbers and it has a planar model over
without reference to the complex numbers and it has a planar model over 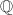 defined by the modular equation. The goal of this section is to prove this unexpected fact and deduce the integrality of
defined by the modular equation. The goal of this section is to prove this unexpected fact and deduce the integrality of 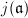 as a consequence.
as a consequence.
To define the modular equation, we need the following lemma.
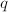 -expansion principle)
Let
-expansion principle)
Let 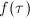 be a modular function with respect to
be a modular function with respect to 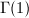 with the
with the 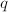 -expansion
-expansion 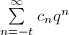 . Then
. Then 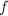 can be expressed as a polynomial of degree
can be expressed as a polynomial of degree 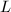 in
in ![$\mathbb{Z}[c_{-t},\ldots,c_0][j(\tau)]$](./latex/latex2png-MinorThesis3_5303128_-5.gif) . In particular, if
. In particular, if 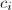 's are integers, then this polynomial has integer coefficients.
's are integers, then this polynomial has integer coefficients.
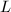 . When
. When 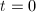 ,
, 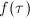 is a holomorphic function on the compact Riemann surface
is a holomorphic function on the compact Riemann surface 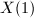 , hence it must be the constant
, hence it must be the constant 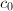 . When
. When 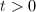 , since
, since 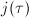 has
has 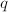 -expansion
-expansion 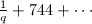 with integer coefficients, the leading term of the
with integer coefficients, the leading term of the 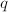 -expansion of
-expansion of 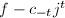 is
is 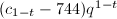 and all the coefficients are in
and all the coefficients are in ![$\mathbb{Z}[c_{1-t},\ldots,c_0]$](./latex/latex2png-MinorThesis3_73701902_-5.gif) . Now applying the induction hypothesis, we know
. Now applying the induction hypothesis, we know ![$f-c_{-t}j^t\in \mathbb{Z}[c_{1-t},\ldots,c_0][j]$](./latex/latex2png-MinorThesis3_102709107_-5.gif) is a polynomial of degree
is a polynomial of degree 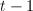 . The lemma follows.
¡õ
. The lemma follows.
¡õ
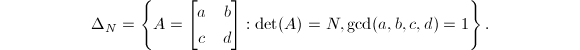 Suppose
Suppose 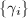 is a set of orbit representatives for the left action of
is a set of orbit representatives for the left action of 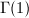 on
on 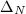 . We define
. We define 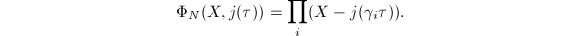 Then the coefficients of
Then the coefficients of 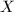 in
in 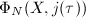 are modular functions of
are modular functions of 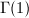 , hence by Lemma 3, these coefficients of
, hence by Lemma 3, these coefficients of 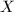 are polynomials in
are polynomials in 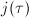 . So
. So 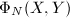 is a polynomial, called the modular polynomial or the modular equation of level
is a polynomial, called the modular polynomial or the modular equation of level 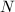 .
.
Since 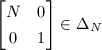 , it follows immediately that
, it follows immediately that 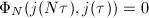 . Also, it is an easy computation ([5, 4.5]) to see that the set of orbit representatives can be chosen as
. Also, it is an easy computation ([5, 4.5]) to see that the set of orbit representatives can be chosen as 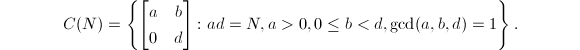
![$\Phi_N(X, Y)\in\mathbb{Z}[X, Y]$](./latex/latex2png-MinorThesis3_139773853_-5.gif) . Moreover, when
. Moreover, when 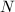 is not a perfect square, the leading coefficient of
is not a perfect square, the leading coefficient of 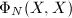 is
is 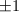 .
.
![$\Phi_N(X, Y)\in\mathbb{Z}[X, Y]$](./latex/latex2png-MinorThesis3_139773853_-5.gif) , it suffices to show that the
, it suffices to show that the 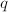 -expansions of
-expansions of 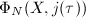 have integer coefficients. Using the orbit representatives in
have integer coefficients. Using the orbit representatives in  , we find that for
, we find that for 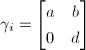 ,
,
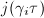 has a Fourier expansion in
has a Fourier expansion in 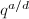 with coefficients in
with coefficients in ![$\mathbb{Z}[\xi]$](./latex/latex2png-MinorThesis3_128867247_-5.gif) where
where 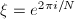 , hence the coefficients of
, hence the coefficients of 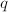 -expansions of
-expansions of 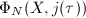 are in
are in ![$\mathbb{Z}[\xi]$](./latex/latex2png-MinorThesis3_128867247_-5.gif) . For an integer
. For an integer  prime to
prime to 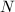 , the map
, the map 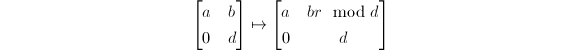 is a permutation of
is a permutation of 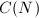 , hence it leaves
, hence it leaves 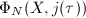 unchanged. But this map has an action
unchanged. But this map has an action 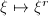 on the coefficients, therefore the coefficients are actually in
on the coefficients, therefore the coefficients are actually in 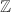 . So
. So ![$\Phi_N(X, Y)\in\mathbb{Z}[X,Y]$](./latex/latex2png-MinorThesis3_65681078_-5.gif) .
.
Now suppose 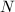 is not a perfect square. The leading coefficient of
is not a perfect square. The leading coefficient of 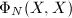 is the same as the leading coefficient of the
is the same as the leading coefficient of the 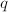 -expansion of
-expansion of 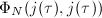 , so let us show that the latter is
, so let us show that the latter is 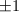 . Now
. Now 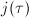 begins with
begins with 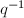 and
and 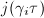 begins with
begins with 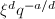 , so since
, so since  is not a perfect square and
is not a perfect square and 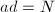 , we know that
, we know that 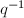 and
and 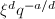 cannot cancel out, hence the leading coefficient of
cannot cancel out, hence the leading coefficient of 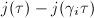 is a root of unity. Multiplying them together, we know that the leading coefficient of
is a root of unity. Multiplying them together, we know that the leading coefficient of 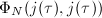 is a root of unity. But we already know it is an integer, hence it must be
is a root of unity. But we already know it is an integer, hence it must be 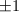 .
¡õ
.
¡õ
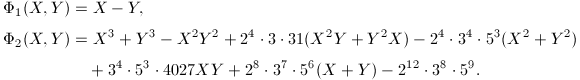 See [3, 13.B] for an algorithm of computing the modular equations. However, it is usually cumbersome to do the computation even for small levels. The
See [3, 13.B] for an algorithm of computing the modular equations. However, it is usually cumbersome to do the computation even for small levels. The 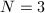 case was computed by Smith in 1878; the
case was computed by Smith in 1878; the 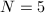 case was computed by Berwick in 1916; the
case was computed by Berwick in 1916; the 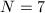 case was computed by Herrmann in 1974 and the
case was computed by Herrmann in 1974 and the 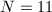 case was computed by Kaltofen and Yui using MACSYMA in 1984. The resulting polynomial
case was computed by Kaltofen and Yui using MACSYMA in 1984. The resulting polynomial 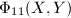 is of degree 21 with coefficients up to
is of degree 21 with coefficients up to 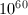 and needs 5 pages to be written out.
and needs 5 pages to be written out.
Now we are in a position to prove the integrality of the singular moduli.
 be an order in an imaginary quadratic field
be an order in an imaginary quadratic field  and
and  be a proper fractional ideal of
be a proper fractional ideal of  . Then
. Then 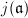 is an algebraic integer of degree
is an algebraic integer of degree 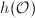 .
.
 in the principal ideal class. Let
in the principal ideal class. Let 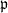 be such a prime. Then
be such a prime. Then 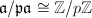 where
where 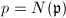 is a prime. We may assume that
is a prime. We may assume that 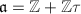 , then
, then 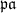 is homothetic to
is homothetic to 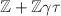 for some
for some 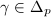 ([3, 11.24]). We know that
([3, 11.24]). We know that 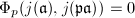 by definition. But
by definition. But 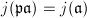 by our choice of
by our choice of 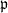 . Hence by Theorem 7,
. Hence by Theorem 7, 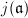 satisfies the polynomial
satisfies the polynomial ![$\Phi_p(X,X)\in\mathbb{Z}[X]$](./latex/latex2png-MinorThesis3_237581038_-5.gif) with leading coefficient
with leading coefficient 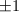 and therefore
and therefore 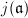 is an algebraic integer. Moreover, we know that its degree is
is an algebraic integer. Moreover, we know that its degree is 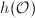 from Theorem 3.
¡õ
from Theorem 3.
¡õ
 Weber's computation of singular moduli
Weber's computation of singular moduli
As an application of Proposition 2, we get an exact sequence 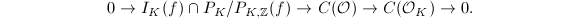 Hence the class numbers of
Hence the class numbers of  and
and 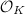 are related by
are related by 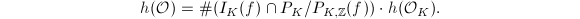 One can show that there is an exact sequence ([3, Exercise 7.30])
One can show that there is an exact sequence ([3, Exercise 7.30]) 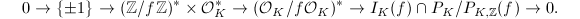 Therefore we are able to reproduce the following formula due to Gauss for the class number of an order
Therefore we are able to reproduce the following formula due to Gauss for the class number of an order  in
in  ([3, 7.24]).
([3, 7.24]).
Our goal in this section is to compute the 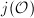 for the orders
for the orders  of class number 1. By Theorem 8, all these singular moduli are rational integers. A famous result about the Gauss class number problem, now known as the Stark-Heegner theorem, says that there only 9 imaginary quadratic fields having class number 1. Moreover, using Theorem 9, we can conclude that there are only four more cases for non-maximal orders of class number 1. More precisely, when
of class number 1. By Theorem 8, all these singular moduli are rational integers. A famous result about the Gauss class number problem, now known as the Stark-Heegner theorem, says that there only 9 imaginary quadratic fields having class number 1. Moreover, using Theorem 9, we can conclude that there are only four more cases for non-maximal orders of class number 1. More precisely, when 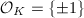 , only
, only 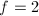 and
and 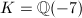 can occur; when
can occur; when 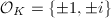 (i.e.,
(i.e., 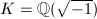 ), only
), only 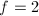 can occur; when
can occur; when 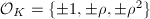 (i.e.,
(i.e., 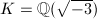 ), only
), only 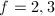 can occur. Since an order
can occur. Since an order  is uniquely determined by its discriminant
is uniquely determined by its discriminant 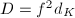 , we may summarize the results as the following theorem.
, we may summarize the results as the following theorem.
 of class number 1. Their discriminants are
of class number 1. Their discriminants are 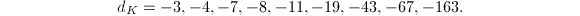 There are only 13 orders
There are only 13 orders  of class number 1. Their discriminants are
of class number 1. Their discriminants are 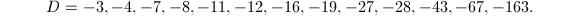
To compute these singular moduli, one may proceed by plugging  into the
into the 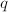 -expansion of
-expansion of 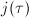 ,
, 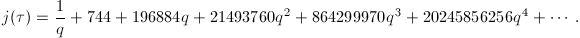 This
This 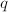 -expansion can be computed via the
-expansion can be computed via the 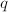 -expansions of
-expansions of 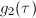 and
and 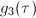 ,
, 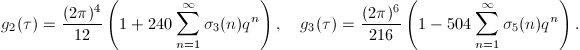 So nowadays we can handle this task using a computer. The numerical method will work pretty well for our purpose since we know a priori that these values are integers. All the 13 singular moduli of integer values are listed in Table 1.
So nowadays we can handle this task using a computer. The numerical method will work pretty well for our purpose since we know a priori that these values are integers. All the 13 singular moduli of integer values are listed in Table 1.
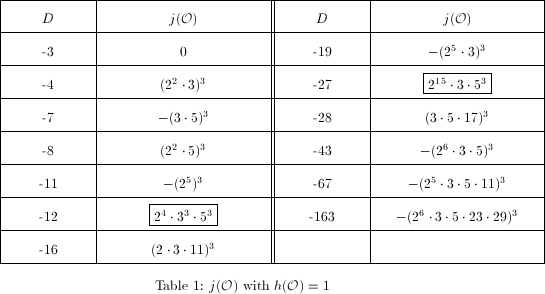
By Theorem 10, we easily obtain a quick method of detecting complex multiplication for elliptic curves over  : if
: if 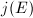 appears in Table 1 , then
appears in Table 1 , then  has complex multiplication with the corresponding order
has complex multiplication with the corresponding order  ; otherwise,
; otherwise,  does not have complex multiplication.
does not have complex multiplication.
However, we are not fully satisfied with this direct computation. For example, it does not explain why most singular moduli in Table 1 (except the two boxed ones) are cubes. Nor does it explain the observation that all these singular moduli are highly divisible. We will try to explain the reasons for these phenomena in the last two sections of this chapter (see Theorem 11, Corollary 1).
Now let us introduce Weber's method for computing the singular moduli of integer values. The main tool of Weber's computation is a class of Weber functions 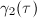 ,
, 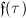 ,
, 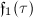 and
and 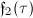 (not to be confused with the Weber function
(not to be confused with the Weber function 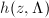 defined earlier).
defined earlier).
![$$\gamma_2(\tau)=\sqrt[{3}]{j(\tau)}=12\frac{g_2(\tau)}{\sqrt[{3}]{\Delta(\tau)}}, $$](./latex/latex2png-MinorThesis3_127498776_.gif) where
where ![$\sqrt[{3}]{\Delta(\tau)}$](./latex/latex2png-MinorThesis3_34206865_-6.gif) is chosen so that it is real-valued on the imaginary axis.
is chosen so that it is real-valued on the imaginary axis.
The Weber function 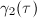 satisfies the following transformation property
satisfies the following transformation property 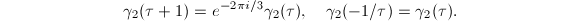 Then it is straightforward to check that
Then it is straightforward to check that 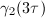 is a modular function with respect to
is a modular function with respect to 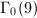 ([3, 12.3]). So
([3, 12.3]). So 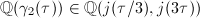 . Moreover, when the order
. Moreover, when the order 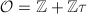 has discriminant prime to 3, we have the following even better relationship between
has discriminant prime to 3, we have the following even better relationship between 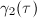 and
and 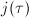 ([3, 12.2]).
([3, 12.2]).
 be an order of discriminant
be an order of discriminant 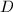 and assume
and assume 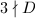 . Set
. Set 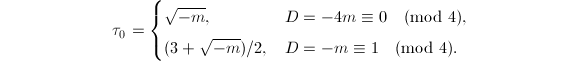 Then
Then 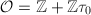 .
. 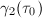 is an algebraic integer and
is an algebraic integer and 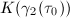 is the ring class field of
is the ring class field of  . Moreover,
. Moreover, 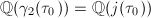 .
.
By the last part of Theorem 11, we know that 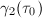 has the same degree as
has the same degree as 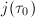 when
when 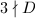 . In particular, when
. In particular, when 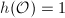 ,
, 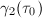 is an integer since
is an integer since 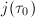 is so. Therefore
is so. Therefore 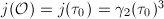 is a cube when
is a cube when 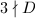 , which coincides with the result listed in Table 1 . The two boxed exceptions
, which coincides with the result listed in Table 1 . The two boxed exceptions 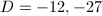 , as expected, are divisible by 3.
, as expected, are divisible by 3.
We may summarize the most important relationship and transformation properties of these Weber functions as follows [3, 12.17, 12.19]. These properties are crucial to Weber's computation of singular moduli.
Now let us use Theorem 12 to compute 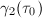 for those orders with discriminants prime to 3. As a consequence, we will be able to compute the singular moduli for those orders easily by raising the corresponding
for those orders with discriminants prime to 3. As a consequence, we will be able to compute the singular moduli for those orders easily by raising the corresponding 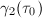 to the third power.
to the third power.
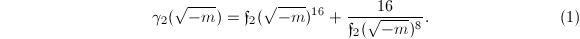 Using the product formula, we get
Using the product formula, we get 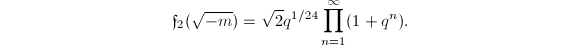 Now applying the inequality
Now applying the inequality 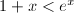 for
for 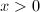 , we obtain
, we obtain 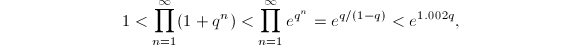 since
since 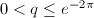 . Using this estimate and plugging
. Using this estimate and plugging 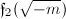 into Equation (1), we get
into Equation (1), we get 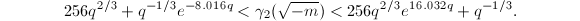 The difference of the upper bound and the lower bound is
The difference of the upper bound and the lower bound is 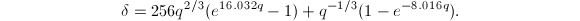 Using the inequality
Using the inequality 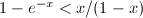 for
for 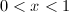 , we have
, we have 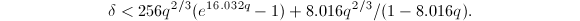 The right hand side is an increasing function in
The right hand side is an increasing function in 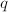 , so
, so 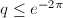 implies
implies 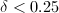 . But
. But 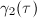 is an integer by Theorem 11, so
is an integer by Theorem 11, so 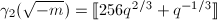 .
.
Next let us consider the case of odd discriminant. The above computation fails, since 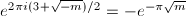 is now negative. However, we can translate
is now negative. However, we can translate 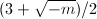 to
to 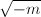 as follows. By Theorem 12 (b) and (d), we know that
as follows. By Theorem 12 (b) and (d), we know that 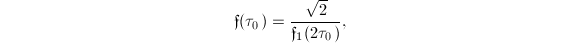 and
and 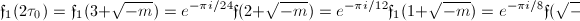 Therefore
Therefore 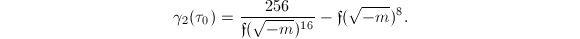 Now a similar argument shows the desired result
Now a similar argument shows the desired result 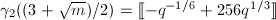 .
¡õ
.
¡õ
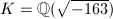 . Then
. Then 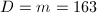 , so by Theorem 11 and Theorem 13, we can compute the singular modulus
, so by Theorem 11 and Theorem 13, we can compute the singular modulus
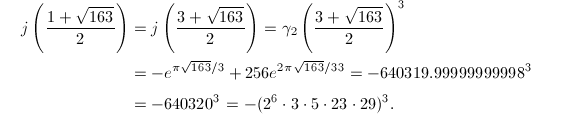 It agrees with the result in Table 1 . We will come back to this example using the powerful Gross-Zagier's theorem in the next section.
It agrees with the result in Table 1 . We will come back to this example using the powerful Gross-Zagier's theorem in the next section.
 Gross-Zagier's theorem on singular moduli
Gross-Zagier's theorem on singular moduli
Gross and Zagier [8] proved a result which completely determines the prime factorization of the norm of the difference between two singular moduli, which in turn justified many classical conjectures on the congruences of singular moduli proposed by Berwick [9]. They provide two proofs of different natures: The first proof, an algebraic proof, is based on Deuring's work on endomorphism rings of elliptic curves mentioned in Chapter 2. The second analytic proof relies on the calculation of the Fourier coefficients of the restriction to the diagonal  of an Eisenstein series of the Hilbert modular group of
of an Eisenstein series of the Hilbert modular group of 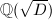 . As the authors remarked, these two methods can be viewed as the special case
. As the authors remarked, these two methods can be viewed as the special case 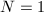 of the theory of local heights of Heegner points on
of the theory of local heights of Heegner points on 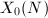 , which generalizes to the groundbreaking Gross-Zagier formula [10].
, which generalizes to the groundbreaking Gross-Zagier formula [10].
In this section, we will first state Gross-Zagier's theorem, then use it to compute several examples and derive some consequences. At the end, we will discuss a bit of the algebraic proof of Gross-Zagier's theorem.
Now consider two orders with discriminants 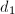 and
and 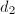 satisfying
satisfying 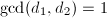 . Let
. Let 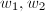 be the numbers of their units and
be the numbers of their units and 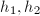 be their class numbers. Let
be their class numbers. Let 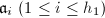 and
and 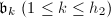 be the representatives of their ideal class groups. Define
be the representatives of their ideal class groups. Define 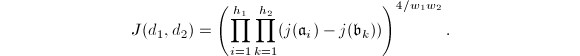 Notice that when
Notice that when 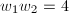 (e.g.,
(e.g., 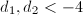 ),
), 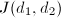 is just the norm of any of the differences
is just the norm of any of the differences 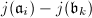 . In general,
. In general, 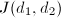 is a certain power of this norm and
is a certain power of this norm and 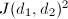 is always an integer.
is always an integer.
To state Gross-Zagier's theorem, let us introduce some notation. Let 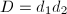 . For a prime
. For a prime  , define
, define 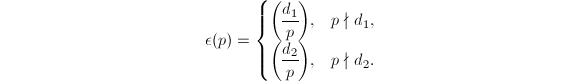 This is well-defined whenever
This is well-defined whenever 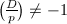 . More generally, if
. More generally, if 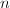 has the prime factorization
has the prime factorization 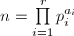 with
with 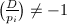 , we define
, we define 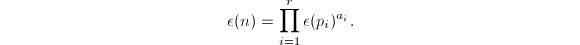 Finally, set
Finally, set 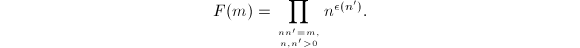 This is well-defined whenever all primes
This is well-defined whenever all primes  dividing
dividing  satisfy
satisfy 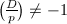 . Now the main theorem is as follows.
. Now the main theorem is as follows.
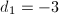 , we know the corresponding
, we know the corresponding 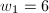 and
and 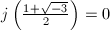 . So in this case,
. So in this case, 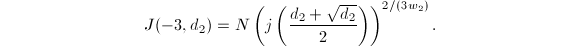 In particular, for
In particular, for 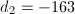 ,
, 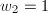 and
and 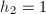 , so we have
, so we have 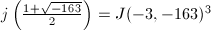 . The factors of
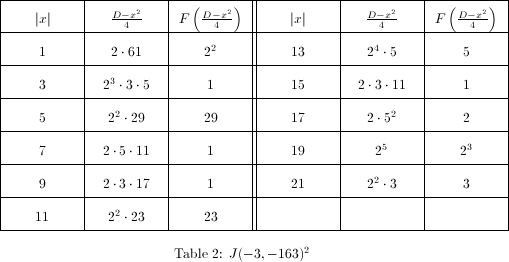
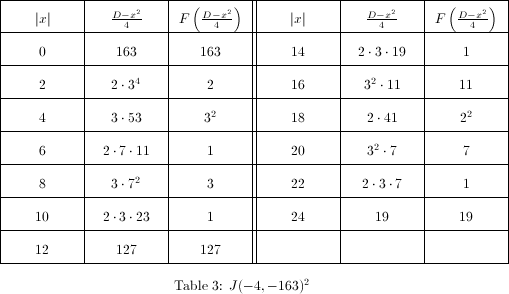
. The factors of 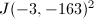 are tabulated in Table 2 , so we can conclude (after figuring out the sign) that
are tabulated in Table 2 , so we can conclude (after figuring out the sign) that 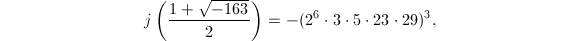 which agrees with our computation in Example 4.
which agrees with our computation in Example 4.
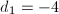 , we know the corresponding
, we know the corresponding 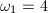 and
and 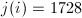 . So in this case,
. So in this case, 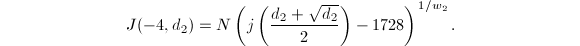 In particular, for
In particular, for 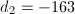 , we have
, we have 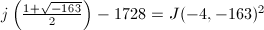 . The factors of
. The factors of 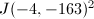 are tabulated in Table 3 , so we can conclude (after figuring out the sign) that
are tabulated in Table 3 , so we can conclude (after figuring out the sign) that 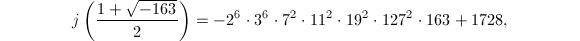 which also agrees with our computation in Example 4.
which also agrees with our computation in Example 4.
As we have noticed, the prime factor of 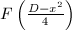 is always a factor of
is always a factor of 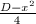 . In fact, we have the following interesting result concerning the function
. In fact, we have the following interesting result concerning the function 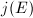 ([3, Exercise 13.15, 13.16]).
([3, Exercise 13.15, 13.16]).
 be a prime dividing
be a prime dividing 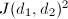 , then
, then  divides a positive integer of the form
divides a positive integer of the form 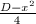 . In particular,
. In particular, 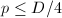 . Moreover,
. Moreover, 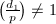 and
and 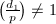 .
.
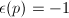 for such
for such  . Without loss of generality, we may assume
. Without loss of generality, we may assume 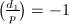 . But
. But 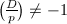 since
since 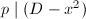 for some
for some  , therefore
, therefore 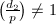 .
¡õ
.
¡õ
Now we can explain the phenomenon we observed in Table 1 . Suppose  is a prime dividing an integer singular modulus of discriminant
is a prime dividing an integer singular modulus of discriminant 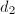 , or equivalently, dividing
, or equivalently, dividing 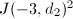 , then by Corollary 1, we have
, then by Corollary 1, we have 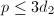 . So these singular moduli have relatively small prime factors, though their own values can be fairly huge.
. So these singular moduli have relatively small prime factors, though their own values can be fairly huge.
Finally, let us come to the algebraic proof of Gross-Zagier's theorem. The proof proceeds locally. As the first step, Gross and Zagier relate the valuation of the difference of two 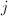 -values to the geometry of elliptic curves and reduce it to a counting problem of isomorphisms between elliptic curves. Next, a generalization of Deuring's lifting theorem will allow one to reduce the problem to counting certain subrings of the endomorphism ring of a supersingular elliptic curve. To complete the proof, Gross and Zagier give a convenient description of a maximal order and its subrings in the rational quaternion algebra ramified at
-values to the geometry of elliptic curves and reduce it to a counting problem of isomorphisms between elliptic curves. Next, a generalization of Deuring's lifting theorem will allow one to reduce the problem to counting certain subrings of the endomorphism ring of a supersingular elliptic curve. To complete the proof, Gross and Zagier give a convenient description of a maximal order and its subrings in the rational quaternion algebra ramified at 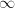 and a prime for explicit computation.
and a prime for explicit computation.
The first step can be viewed as an interesting geometrical interpretation of the difference of 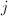 -values.
-values.
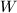 be a complete discrete valuation ring whose quotient field has characteristic zero and whose residue field is algebraically closed and has characteristic
be a complete discrete valuation ring whose quotient field has characteristic zero and whose residue field is algebraically closed and has characteristic 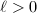 (e.g.,
(e.g., 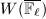 ). Let
). Let 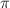 be its uniformizer and
be its uniformizer and 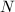 be its normalized valuation. Let
be its normalized valuation. Let 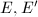 be elliptic curves defined over
be elliptic curves defined over 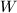 with good reduction and
with good reduction and 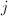 -invariants
-invariants 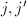 . Denote the set of isomorphisms from
. Denote the set of isomorphisms from  to
to 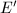 defined over
defined over 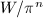 by
by 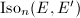 . Then
. Then 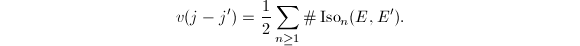
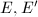 are isomorphic over the algebraically closed field
are isomorphic over the algebraically closed field 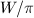 , otherwise both sides are zero. Denote
, otherwise both sides are zero. Denote 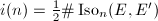 , then
, then 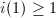 .
.
Let us consider the case when 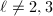 for simplicity. Change models for
for simplicity. Change models for 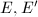 with simplified Weierstrass equations
with simplified Weierstrass equations 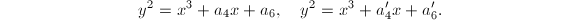
By definition, we have 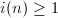 if and only if we can solve the congruences
if and only if we can solve the congruences
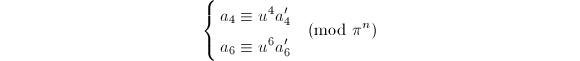 simultaneously for some unit
simultaneously for some unit 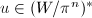 . In this case
. In this case 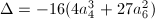 , and at least one of
, and at least one of 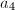 and
and 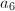 is a unit in
is a unit in 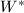 since
since  has good reduction mod
has good reduction mod 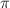 .
.
If 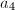 is a unit in
is a unit in 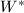 , then
, then 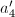 is also a unit. By changing models we may assume that
is also a unit. By changing models we may assume that 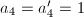 . Then
. Then 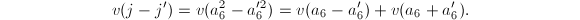 On the other hand, the congruences become
On the other hand, the congruences become
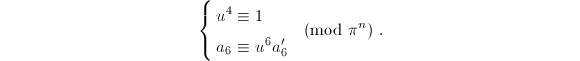 We may possibly modify
We may possibly modify 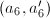 by
by 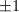 so that
so that 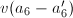 is maximal. Then
is maximal. Then
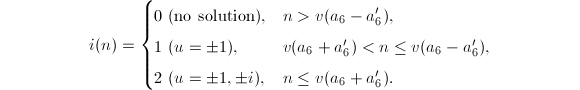 We get
We get 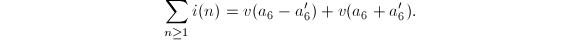 So the theorem holds in this case.
So the theorem holds in this case.
If 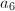 is a unit in
is a unit in 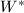 , then
, then 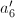 is also a unit. Similarly by changing models we may assume that
is also a unit. Similarly by changing models we may assume that 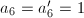 . Then
. Then
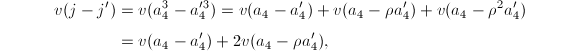 where
where 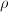 is a primitive cube root of unity in
is a primitive cube root of unity in 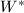 . On the other hand, the congruences become
. On the other hand, the congruences become
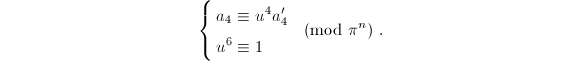 We may possibly modify
We may possibly modify 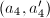 by
by 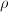 or
or 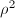 so that
so that 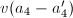 is maximal. Then
is maximal. Then
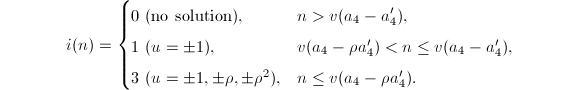 We get
We get 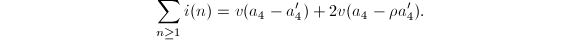 This completes the proof.
¡õ
This completes the proof.
¡õ
For simplicity, we will assume 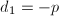 is a prime from now on (for the general case, see [11]). Let
is a prime from now on (for the general case, see [11]). Let 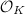 be the ring of integers of
be the ring of integers of 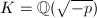 . Let
. Let  be an elliptic curve over
be an elliptic curve over 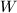 with complex multiplication by
with complex multiplication by 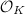 and with
and with 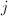 -invariant
-invariant 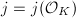 . For our purpose, we need to calculate
. For our purpose, we need to calculate 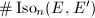 where
where 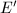 is an elliptic curve over
is an elliptic curve over 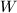 with complex multiplication by some ring
with complex multiplication by some ring ![$\mathbb{Z}[w]$](./latex/latex2png-MinorThesis3_28092862_-5.gif) of discriminant
of discriminant 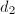 . We can rewrite
. We can rewrite 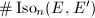 in a manner which only depends on
in a manner which only depends on  . Suppose
. Suppose 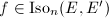 , then
, then 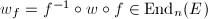 is an endomorphism of
is an endomorphism of  mod
mod 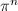 , which has the same norm, trace and action on tangent space as
, which has the same norm, trace and action on tangent space as 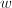 . Namely,
. Namely, 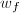 belongs to the set
belongs to the set 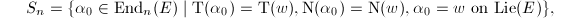 Conversely, every element of
Conversely, every element of 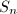 is of the form
is of the form 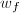 for some unique
for some unique 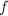 ensured by the following lifting theorem, which is a refinement of Deuring's lifting theorem ([12, 14.14]).
ensured by the following lifting theorem, which is a refinement of Deuring's lifting theorem ([12, 14.14]).
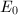 be an elliptic curve over
be an elliptic curve over 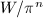 and
and 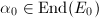 . Assume that
. Assume that ![$\mathbb{Z}[\alpha_0]$](./latex/latex2png-MinorThesis3_162559240_-5.gif) is a
is a 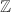 -module of rank 2 and is integrally closed in its quotient field. Suppose
-module of rank 2 and is integrally closed in its quotient field. Suppose 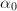 induces multiplication by a quadratic element
induces multiplication by a quadratic element 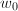 on
on 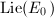 . If there exists
. If there exists 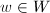 such that
such that 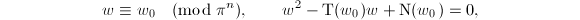 then there exists an elliptic curve
then there exists an elliptic curve  over
over 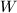 and
and 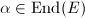 , such that
, such that 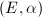 reduces to
reduces to 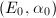 mod
mod 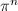 and
and 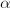 induces multiplication by
induces multiplication by 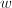 on
on 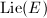 . Moreover, if
. Moreover, if 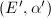 is another lifting, then there is a commutative diagram
is another lifting, then there is a commutative diagram ![$$\xymatrix{E \ar[r]^\alpha\ar[d]_{\cong} & E \ar[d]^{\cong}\\ E'\ar[r]^{\alpha'} & E'.}$$](./latex/latex2png-MinorThesis3_69540335_.gif)
Now by Theorem 16, we reduce to the counting problem of 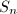 .
.
When 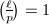 ,
,  splits in
splits in 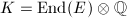 , so
, so  has ordinary reduction mod
has ordinary reduction mod 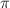 and
and 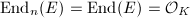 ([12, 13.12]). But
([12, 13.12]). But 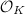 contains no elements of discriminant
contains no elements of discriminant 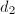 , so
, so 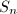 is empty for all
is empty for all 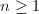 . (Another way to say this: if two elliptic curves
. (Another way to say this: if two elliptic curves  and
and 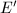 with complex multiplication have the isomorphic reduction
with complex multiplication have the isomorphic reduction 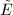 , then the reduction
, then the reduction 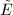 must be supersingular, since two different orders
must be supersingular, since two different orders 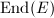 and
and 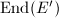 have to embed into
have to embed into 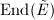 simultaneously.)
simultaneously.)
So we only need to consider the case 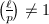 and
and  has supersingular reduction. Then
has supersingular reduction. Then 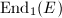 is a maximal order in the rational quaternion algebra
is a maximal order in the rational quaternion algebra 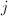 ramified at
ramified at 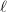 and
and 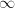 by Theorem 8. The algebra
by Theorem 8. The algebra 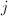 can be desribed explicitly as a subring of
can be desribed explicitly as a subring of 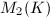 ,
, 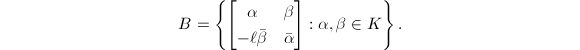 The subrings
The subrings 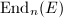 can also be desribed explicitly. Using these descriptions, it turns out that in many cases
can also be desribed explicitly. Using these descriptions, it turns out that in many cases 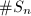 equals to
equals to  times the number of the solutions
times the number of the solutions 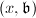 (under certain conditions on
(under certain conditions on 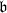 ) of the equation
) of the equation 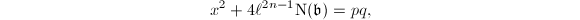 where we assume
where we assume 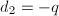 is a prime . The more precise result is the following.
is a prime . The more precise result is the following.
The main Theorem 14 now can be derived directly from Equation 2using the formula 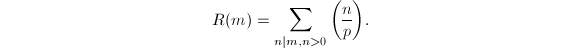 Unfortunately, we will omit the details here.
Unfortunately, we will omit the details here.
References
[1]Introduction to the Arithmetic Theory of Automorphic Functions, Princeton University Press, 1971.
[2]Complex multimplication, Algebraic Number Theory, London Mathematical Society, 1967, 292-296.
[3]Primes of the Form $X^2 + ny^2$: Fermat, Class Field Theory, and Complex Multiplication, John Wiley \& Sons, 1989.
[4]Algebraic Number Theory, Springer, 1994.
[5]Complex multimplication and explicit class field theory, 1996, Senior thesis, Harvard University.
[6]Advanced Topics in the Arithmetic of Elliptic Curves, Springer, 1994.
[7]A First Course in Modular Forms, Springer, 2010.
[8]On singular moduli, J. reine angew. Math 355 (1985), no.2, 191--220.
[9]Modular Invariants Expressible in Terms of Quadratic and Cubic Irrationalities, Proc. London Math. Soc. 28 (1927), 53-69.
[10]Heegner points and derivatives of L-series, Invent. math 84 (1986), no.2, 225--320.
[11]Prime factorization of singular moduli, Brown University, 1984.
[12]Elliptic Functions, Springer, 1987.
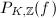 is called the ring class field of
is called the ring class field of 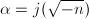 as in Remark
as in Remark ![$$h({\cal O})=\frac{h({\cal O}_K)f}{[{\cal O}_K^*:{\cal O}^*]}\prod_{p\mid f}\left(1-\legendre{d_K}{p}\frac{1}{p}\right).$$](./latex/latex2png-MinorThesis3_215696511_.gif)
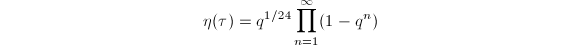 be the Dedekind
be the Dedekind 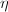 -function. We define the Weber functions
-function. We define the Weber functions
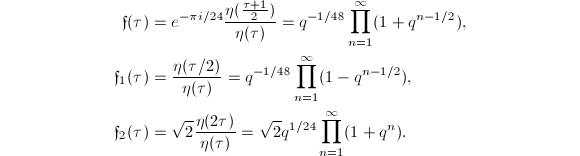
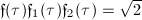 .
.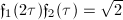 .
.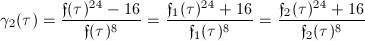 .
.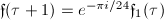 ,
, 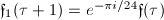 ,
, 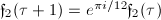 .
.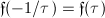 ,
, 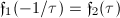 ,
, 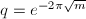 . Then for
. Then for 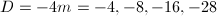 ,
, 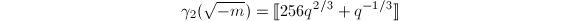 and for
and for 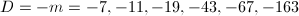 ,
, 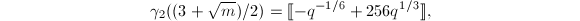 where
where 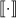 is the nearest integer function.
is the nearest integer function.
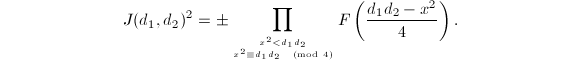
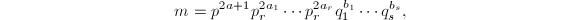 where
where 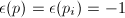 and
and 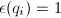 . In this case,
. In this case, 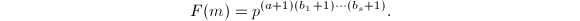
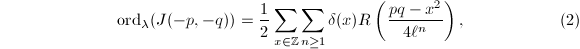 where
where 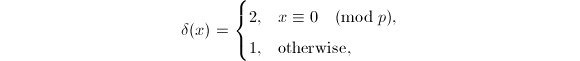 and
and 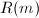 is the number of ideals of
is the number of ideals of