This is a note prepared for the Harvard Mazur's torsion theorem seminar (see the references listed there). This talk will tie up several loose ends from the previous talks. We will recall the construction of the Eisenstein prime quotient of 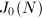 and show that the
and show that the 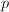 -torsion of its Neron model is an admissible group scheme. This allows us to run fppf descent and bound the Mordell-Weil rank of the Eisenstein prime quotient. As an immediate consequence, it follows that the number of rational points on
-torsion of its Neron model is an admissible group scheme. This allows us to run fppf descent and bound the Mordell-Weil rank of the Eisenstein prime quotient. As an immediate consequence, it follows that the number of rational points on 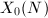 is finite whenever it is not obviously infinite, for
is finite whenever it is not obviously infinite, for 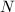 a prime.
a prime.
 Eisenstein quotients
Eisenstein quotients
We fix a prime number 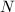 throughout this talk. Recall that the Eisenstein ideal
throughout this talk. Recall that the Eisenstein ideal 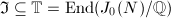 is defined to be the ideal generated by
is defined to be the ideal generated by 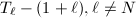 , and
, and 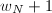 and we have seen from Cheng-Chiang's talk that
and we have seen from Cheng-Chiang's talk that 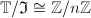 , where
, where 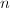 is the numerator of
is the numerator of 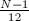 . So the maximal ideals of
. So the maximal ideals of 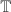 containing
containing 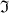 are exactly the Eisenstein primes
are exactly the Eisenstein primes 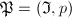 ,
, 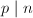 , with residue fields
, with residue fields 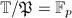 .
.
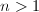 (i.e.,
(i.e., 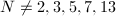 ), if and only if the genus
), if and only if the genus 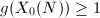 .
.
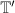 generated by
generated by 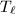 and
and 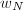 as endomorphisms on all holomorphic modular forms
as endomorphisms on all holomorphic modular forms 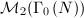 of weight 2. Since
of weight 2. Since 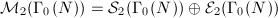 decomposes as the direct sum of the space of cusp forms and the space of Eisenstein series (which is one-dimensional, generated by
decomposes as the direct sum of the space of cusp forms and the space of Eisenstein series (which is one-dimensional, generated by 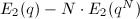 ), restricting the action of
), restricting the action of 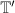 on
on 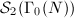 and
and 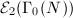 gives two inclusions
gives two inclusions 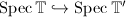 and
and 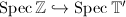 . The latter
. The latter 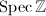 is naturally called the Eisenstein line. So an Eisenstein prime
is naturally called the Eisenstein line. So an Eisenstein prime  can be viewed as the intersection of
can be viewed as the intersection of 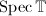 with the Eisenstein line, reflecting the congruence relation between the Eisenstein series and a certain cusp form modulo
with the Eisenstein line, reflecting the congruence relation between the Eisenstein series and a certain cusp form modulo 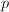 : there exists a cusp form whose
: there exists a cusp form whose 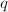 -expansion modulo
-expansion modulo 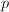 coincides with the Hecke eigenvector
coincides with the Hecke eigenvector 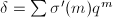 (whose eigenvalues are exactly
(whose eigenvalues are exactly 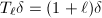 and
and 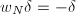 ). This congruence relation is the key input for the existence of an Eisenstein prime
). This congruence relation is the key input for the existence of an Eisenstein prime  .
.
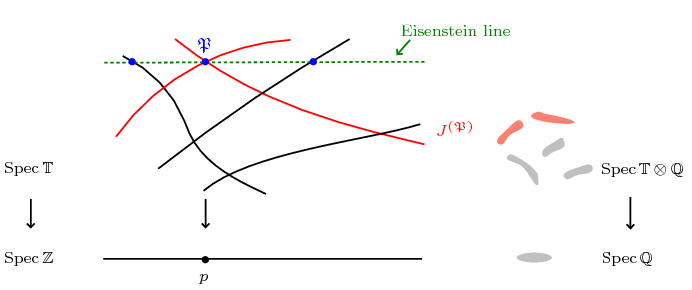 |
| Eisenstein primes |
 we can construct a canonical quotient of
we can construct a canonical quotient of 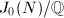 . Since
. Since 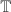 is a free
is a free 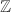 -module of finite rank, it is a flat extension of
-module of finite rank, it is a flat extension of 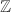 and has Krull dimension 1 by going-down (so our picture above is accurate in this sense). Since
and has Krull dimension 1 by going-down (so our picture above is accurate in this sense). Since 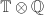 is a finite dimensional vector space, it is Artinian and we have already seen that it is actually a product of totally real fields
is a finite dimensional vector space, it is Artinian and we have already seen that it is actually a product of totally real fields 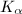 (due to the fact that
(due to the fact that 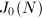 has semistable reduction). The embedding
has semistable reduction). The embedding  then gives a bijection between minimal prime ideals of
then gives a bijection between minimal prime ideals of  and prime ideals of
and prime ideals of 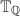 (which are all maximal), and in turn a bijection with the totally real fields
(which are all maximal), and in turn a bijection with the totally real fields 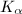 , and the isogenous factors of
, and the isogenous factors of 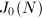 . We define the Eisenstein prime quotient
. We define the Eisenstein prime quotient 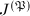 to be the unique optimal quotient (i.e., quotient by an abelian subvariety of
to be the unique optimal quotient (i.e., quotient by an abelian subvariety of 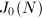 ) whose isogenous factors correspond to minimal prime ideals contained in
) whose isogenous factors correspond to minimal prime ideals contained in  . Then
. Then 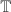 also acts on
also acts on 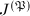 . To visualize, each isogenous factor of
. To visualize, each isogenous factor of 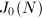 corresponds to an irreducible component of
corresponds to an irreducible component of 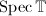 and
and 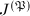 simply corresponds to all the components passing through the Eisenstein prime
simply corresponds to all the components passing through the Eisenstein prime  .
.
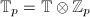 be the completion of
be the completion of 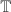 at
at 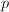 . Then
. Then 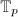 is a free
is a free 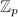 -module of finite rank, hence is a semilocal ring and
-module of finite rank, hence is a semilocal ring and 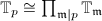 , where
, where 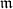 runs over all maximal ideals containing
runs over all maximal ideals containing 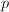 . Then
. Then 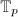 acts on the
acts on the 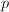 -adic Tate module
-adic Tate module 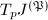 . Moreover, the rational
. Moreover, the rational 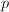 -adic Tate module
-adic Tate module 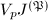 can be identified as the direct product of
can be identified as the direct product of 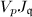 , where
, where 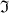 runs over all minimal primes contained in
runs over all minimal primes contained in  . The action of
. The action of 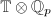 on each
on each 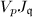 factors through
factors through 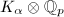 , where
, where 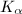 is the totally real field corresponding to
is the totally real field corresponding to 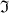 . It follows that the action of
. It follows that the action of 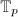 on
on 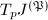 factors through
factors through 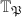 .
.
Our main goal is to prove the following
 be an Eisenstein prime and
be an Eisenstein prime and 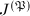 be the Eisenstein prime quotient of
be the Eisenstein prime quotient of 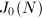 . Then
. Then 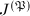 has rank 0, i.e.,
has rank 0, i.e., 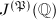 is finite.
is finite.
As an immediate application, we obtain a "conceptual" proof of the following interesting result.
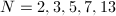 ,
, 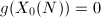 and the two cusps are rational, hence
and the two cusps are rational, hence 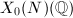 is clearly infinite in these cases. In the case
is clearly infinite in these cases. In the case 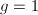 , we have seen an example of explicitly computing rational points for
, we have seen an example of explicitly computing rational points for 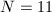 in Erick's talk. One can also quote the big theorem of Faltings for
in Erick's talk. One can also quote the big theorem of Faltings for 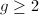 , but Mazur's method can certainly say more about
, but Mazur's method can certainly say more about 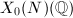 .
.
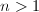 , so there exists a nontrivial Eisenstein prime quotient
, so there exists a nontrivial Eisenstein prime quotient 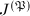 (Remark 2). Since
(Remark 2). Since 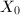 is an irreducible projective curve, the composite map
is an irreducible projective curve, the composite map 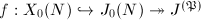 is either constant or a finite morphism onto a curve. Because the image of
is either constant or a finite morphism onto a curve. Because the image of 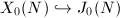 generates
generates 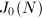 as a group, the image of
as a group, the image of 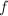 generates
generates 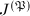 as a group (which has positive dimension) and hence
as a group (which has positive dimension) and hence 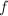 cannot be constant. So
cannot be constant. So 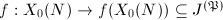 is a finite morphism of curves. By Theorem 1, we know that
is a finite morphism of curves. By Theorem 1, we know that 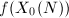 has only finite rational points, thus so does
has only finite rational points, thus so does 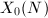 .
¡õ
.
¡õ
 Eisenstein descent
Eisenstein descent
Recall that a quasi-finite flat separated group scheme 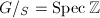 (finite flat over
(finite flat over ![$S'{}=\Spec \mathbb{Z}[1/N]$](./latex/latex2png-EisensteinDescent_227077503_-5.gif) ) is called (
) is called (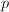 )-admissible if
)-admissible if 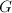 is killed by a power of
is killed by a power of 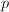 and
and 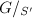 admits a filtration by finite flat group schemes such that the successive quotients are either
admits a filtration by finite flat group schemes such that the successive quotients are either  or
or 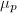 . Bao has explained in his talk that the admissibility can be detected on the associated
. Bao has explained in his talk that the admissibility can be detected on the associated 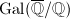 -module
-module 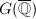 and also proved the following easy but crucial estimate.
and also proved the following easy but crucial estimate.
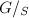 be an admissible group scheme. Then
be an admissible group scheme. Then 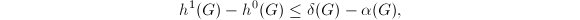 where
where 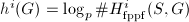 ,
, 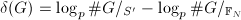 is the defect and
is the defect and 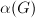 is the number of
is the number of  's in the successive quotients of
's in the successive quotients of 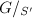 .
.
The proof of Theorem 1 relies on the following admissibility result, which allows one to bound the Mordell-Weil rank of 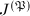 via Theorem 3 and is the major motivation to introduce the notion of the Eisenstein quotients.
via Theorem 3 and is the major motivation to introduce the notion of the Eisenstein quotients.
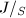 be the Neron model of the Eisenstein prime quotient
be the Neron model of the Eisenstein prime quotient 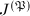 . Then its
. Then its 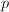 -torsion
-torsion ![$J[p]/_{S}$](./latex/latex2png-EisensteinDescent_186085911_-5.gif) is an admissible group scheme.
is an admissible group scheme.
Assuming Theorem 4, we can finish the proof of main Theorem 1 using a standard descent argument.
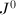 be the fiberwise connected component of
be the fiberwise connected component of 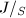 . We know from George's talk that
. We know from George's talk that 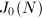 has good reduction outside
has good reduction outside 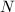 and toric reduction at
and toric reduction at 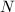 , hence so does
, hence so does 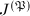 . Then
. Then ![$[p]:J^0\rightarrow J^0$](./latex/latex2png-EisensteinDescent_200151626_-5.gif) is a surjective morphism of schemes (which can be checked on geometric points, Lemma 0487) as there is no unipotent part in
is a surjective morphism of schemes (which can be checked on geometric points, Lemma 0487) as there is no unipotent part in 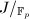 . Since
. Since ![$[p]$](./latex/latex2png-EisensteinDescent_2132972_-5.gif) is also fppf (but not etale since
is also fppf (but not etale since 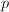 is not invertible on
is not invertible on 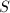 ),
), 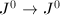 is a surjection as fppf sheaves (Lemma 05VM, but not as etale sheaves). So we obtain an exact sequence of fppf sheaves
is a surjection as fppf sheaves (Lemma 05VM, but not as etale sheaves). So we obtain an exact sequence of fppf sheaves ![$$0\rightarrow J^0[p]\rightarrow J^0\rightarrow J^0\rightarrow 0,$$](./latex/latex2png-EisensteinDescent_30014344_.gif) which induces an exact sequence in fppf cohomology
which induces an exact sequence in fppf cohomology ![$$0\rightarrow J^0(\mathbb{Z})/p J^0(\mathbb{Z})\rightarrow H^1_\mathrm{fppf}(S, J^0[p])\rightarrow H^1_\mathrm{fppf}(S, J^0)[p]\rightarrow 0.$$](./latex/latex2png-EisensteinDescent_124068233_.gif) The first inclusion implies that
The first inclusion implies that 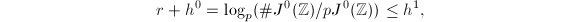 where
where  is the rank of the abelian group
is the rank of the abelian group 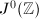 .
.
On the other hand, by Theorem 4, ![$J^0[p]$](./latex/latex2png-EisensteinDescent_2122477_-5.gif) is also admissible. So Theorem 3 gives
is also admissible. So Theorem 3 gives 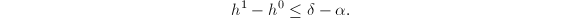 Let
Let 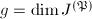 . Using the toric reduction at
. Using the toric reduction at 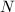 , we can compute
, we can compute ![$\delta(J^0[p])=2g-g=g$](./latex/latex2png-EisensteinDescent_192871403_-5.gif) . Replacing
. Replacing 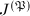 by
by 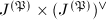 (notice this does not change the reduction type), we may assume that
(notice this does not change the reduction type), we may assume that ![$J^0[p]$](./latex/latex2png-EisensteinDescent_2122477_-5.gif) is its own Cartier dual, then
is its own Cartier dual, then ![$\alpha(J^0[p])=2g/2=g$](./latex/latex2png-EisensteinDescent_21691371_-5.gif) . Then we have
. Then we have 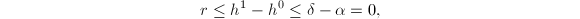 hence
hence 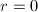 . Finally, by then Neron mapping property,
. Finally, by then Neron mapping property, 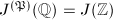 , which has the same rank as
, which has the same rank as 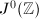 . This completes the proof.
¡õ
. This completes the proof.
¡õ
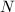 is crucial: the defect
is crucial: the defect 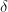 gets bigger when there are more unipotent parts and so the bound on the rank
gets bigger when there are more unipotent parts and so the bound on the rank  gets higher. Also etale cohomology does not fulfill our purpose since
gets higher. Also etale cohomology does not fulfill our purpose since ![$[p]$](./latex/latex2png-EisensteinDescent_2132972_-5.gif) is not invertible over the base
is not invertible over the base 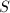 . This point was already illustrated in Tom's talk when performing 19-descent on
. This point was already illustrated in Tom's talk when performing 19-descent on 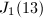 .
.
![$H^1_\mathrm{fppf}(S, J^0[p])$](./latex/latex2png-EisensteinDescent_192281076_-8.gif) has a purely geometric description as
has a purely geometric description as ![$J^0[p]$](./latex/latex2png-EisensteinDescent_2122477_-5.gif) -torsors without using cocycles and coboundaries: since
-torsors without using cocycles and coboundaries: since ![$J^0[p]$](./latex/latex2png-EisensteinDescent_2122477_-5.gif) itself is fppf over
itself is fppf over 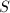 , every
, every ![$J^0[p]$](./latex/latex2png-EisensteinDescent_2122477_-5.gif) -torsor is automatically fppf over
-torsor is automatically fppf over 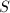 .
.
 Admissibility
Admissibility
It remains to prove the key admissibility result for ![$J[p]/_{S}$](./latex/latex2png-EisensteinDescent_186085911_-5.gif) (Theorem 4), where
(Theorem 4), where 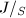 is the Neron model of
is the Neron model of 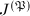 . It suffices to check that the finite Galois module
. It suffices to check that the finite Galois module $](./latex/latex2png-EisensteinDescent_88214082_-5.gif) has composition factors
has composition factors  or
or 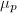 . We will utilize the classical theorem of Brauer-Nesbitt.
. We will utilize the classical theorem of Brauer-Nesbitt.
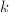 be any field and
be any field and 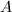 be a
be a 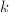 -algebra. Let
-algebra. Let 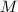 ,
, 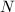 be two
be two 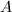 -modules which are finite-dimensional as
-modules which are finite-dimensional as 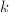 -vector spaces. If for all
-vector spaces. If for all  , the characteristic polynomials of
, the characteristic polynomials of  on
on 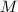 and
and 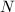 are equal, then
are equal, then 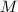 and
and 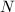 have the same composition factors.
have the same composition factors.
![$A=\mathbb{F}_p[G]$](./latex/latex2png-EisensteinDescent_104079443_-5.gif) will be the group algebra of a finite Galois group
will be the group algebra of a finite Galois group 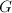 . Since we are in characteristic
. Since we are in characteristic 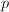 , we need the full characteristic polynomials rather than merely the character of
, we need the full characteristic polynomials rather than merely the character of 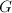 .
.
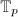 on
on ![$T_pJ[p]$](./latex/latex2png-EisensteinDescent_1962418_-5.gif) factors through
factors through 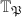 (Remark 4), we know that the action of
(Remark 4), we know that the action of 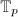 on
on ![$J[p]$](./latex/latex2png-EisensteinDescent_2132934_-5.gif) factors through
factors through 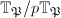 , which is a finite
, which is a finite 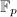 -vector space, hence is an Artinian local ring and the maximal ideal
-vector space, hence is an Artinian local ring and the maximal ideal  is nilpotent in
is nilpotent in 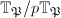 . In other words,
. In other words, 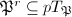 for some
for some 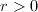 .
¡õ
.
¡õ
So to finish the proof of Theorem 4, it suffices to prove
![$$J_0(N)[\mathfrak{P}^r]\supseteq \mathfrak{P}J_0(N)[\mathfrak{P}^r]\supseteq \cdots\supseteq \mathfrak{P}^rJ_0(N)[\mathfrak{P}^r]=0.$$](./latex/latex2png-EisensteinDescent_159400107_.gif) It suffices to show that
It suffices to show that ![$V=\mathfrak{P}^iJ_0(N)[\mathfrak{P}^r]/\mathfrak{P}^{i+1} J_0(N)[\mathfrak{P}^r]$](./latex/latex2png-EisensteinDescent_20480940_-5.gif) is admissible. Let
is admissible. Let 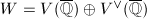 , then
, then 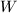 is a finite
is a finite 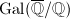 -module and the action of
-module and the action of 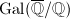 on
on 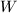 factors through a finite quotient
factors through a finite quotient 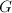 , i.e.,
, i.e., 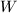 is a
is a ![$\mathbb{F}_p[G]$](./latex/latex2png-EisensteinDescent_61968467_-5.gif) -module. For any element
-module. For any element 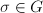 , we can find some
, we can find some 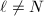 such that
such that 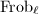 and
and 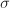 are in the same conjugacy class by Chebotarev. By the Eichler-Shimura relation, we also know that
are in the same conjugacy class by Chebotarev. By the Eichler-Shimura relation, we also know that 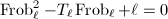 . Since
. Since  kills
kills 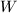 ,
, 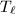 acts as
acts as  on
on 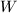 , hence the eigenvalue of
, hence the eigenvalue of 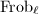 must be either 1 or
must be either 1 or 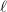 . Since taking the Cartier dual interchanges the eigenvalues 1 and
. Since taking the Cartier dual interchanges the eigenvalues 1 and 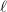 , we know that the characteristic polynomial of
, we know that the characteristic polynomial of 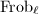 on
on 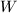 is equal to
is equal to 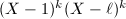 , where
, where 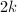 is the dimension of
is the dimension of 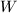 as an
as an 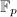 -vector space. So the characteristic polynomial of
-vector space. So the characteristic polynomial of 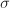 on
on 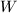 is also
is also 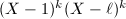 . On the other hand, the characteristic polynomial of
. On the other hand, the characteristic polynomial of 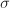 on the admissible group
on the admissible group  (we can always choose
(we can always choose 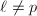 and enlarge
and enlarge 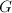 such that
such that 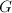 acts on it) is also equal to
acts on it) is also equal to 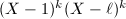 . We now apply Brauer-Nesbitt's Theorem 5 to
. We now apply Brauer-Nesbitt's Theorem 5 to ![$A=\mathbb{F}_p[G]$](./latex/latex2png-EisensteinDescent_104079443_-5.gif) and
and  ,
, 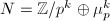 to conclude that
to conclude that 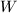 is admissible, and thus
is admissible, and thus 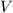 is admissible as required.
¡õ
is admissible as required.
¡õ
![$J[p]\subseteq J_0(N)[\mathfrak{P}^r]$](./latex/latex2png-EisensteinDescent_165600673_-5.gif) for some
for some ![$J_0(N)[\mathfrak{P}^r]$](./latex/latex2png-EisensteinDescent_71075367_-5.gif) is an admissible group scheme for any
is an admissible group scheme for any