These are expanded notes prepared for a talk in a learning seminar on Kato's Euler systems, Fall 2016 at Columbia. We motivate the statement of Kato's explicit reciprocity laws and sketch his proof using 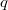 -expansions. Our main references are [1] and [2].
-expansions. Our main references are [1] and [2].
 Hilbert symbols
Hilbert symbols
Recall the classical quadratic reciprocity law: if  ,
,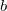 are odd positive coprime integers, then the quadratic residue symbols satisfies
are odd positive coprime integers, then the quadratic residue symbols satisfies 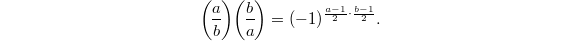 An equivalent formulation in terms of Hilbert symbols (using the product formula) is that for
An equivalent formulation in terms of Hilbert symbols (using the product formula) is that for 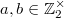 , the Hilbert symbol
, the Hilbert symbol 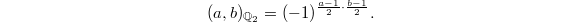
More generally for 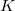 a
a 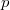 -adic field containing
-adic field containing 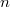 -th roots of unity, Kummer theory/class field theory provide the Hilbert symbol
-th roots of unity, Kummer theory/class field theory provide the Hilbert symbol ![$$(a,b)_K: K^\times/(K^\times)^n\times K^\times/(K^\times)^n\rightarrow \mu_n,\quad (a,b)=\frac{\Art(a)(\sqrt[n]{b})}{\sqrt[n]{b}}.$$](./latex/ExplicitReciprocity/latex2png-ExplicitReciprocity_222854211_.gif) The quadratic reciprocity law can be viewed an explicit formula for
The quadratic reciprocity law can be viewed an explicit formula for 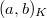 in the case
in the case 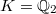 and
and 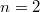 . So the key to explicating higher reciprocity laws is to give explicit formulas for
. So the key to explicating higher reciprocity laws is to give explicit formulas for 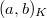 in the wild case
in the wild case 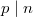 . This is more difficult and such a prototype dates back to Kummer [3].
. This is more difficult and such a prototype dates back to Kummer [3].
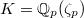 with uniformizer
with uniformizer 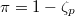 . For
. For 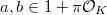 , we have
, we have 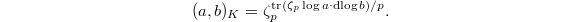 Here
Here 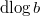 means the logarithmic derivative
means the logarithmic derivative 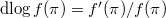 with respect to
with respect to  of any representation
of any representation 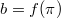 (
(![$f\in \mathbb{Z}_p[ [T]]$](./latex/ExplicitReciprocity/latex2png-ExplicitReciprocity_154539563_-5.gif) ) and
) and 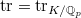 .
.
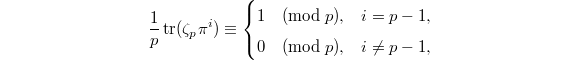 we know that the exponent appearing above is the same as the coefficient of
we know that the exponent appearing above is the same as the coefficient of 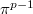 in
in 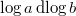 (= the formal residue of
(= the formal residue of 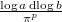 ).
).
 Classical explicit reciprocity laws
Classical explicit reciprocity laws
To facilitate generalization, let us reinterpret Kummer's formula as an explicit formula for the Hilbert symbol using a "dual exponential map". Consider the 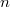 -th layer of the cyclotomic tower
-th layer of the cyclotomic tower 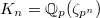 (so
(so 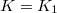 ). We have the
). We have the 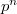 -th Hilbert symbol associated to
-th Hilbert symbol associated to 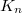 ,
, 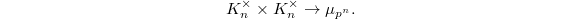 Fix a compatible system of
Fix a compatible system of 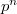 -roots of unity
-roots of unity 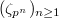 . Sending
. Sending 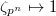 induces a (no longer Galois equivariant) pairing
induces a (no longer Galois equivariant) pairing 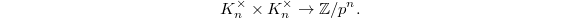 Now fix the first factor to be
Now fix the first factor to be 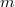 and take inverse limit over
and take inverse limit over 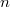 (with respect to norm maps) for the second factor, we obtain a pairing
(with respect to norm maps) for the second factor, we obtain a pairing 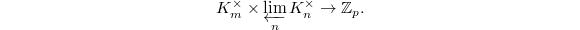 This gives a map
This gives a map 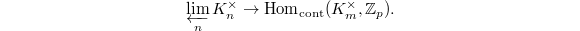 By precomposing with the exponential map
By precomposing with the exponential map 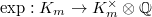 , we obtain a map
, we obtain a map 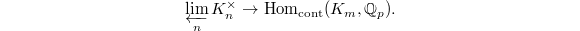 The trace pairing
The trace pairing 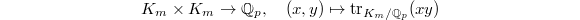 identifies
identifies 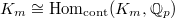 , so at last we obtain a map
, so at last we obtain a map 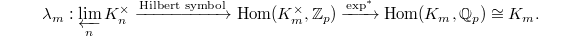
The classical explicit reciprocity law (Artin—Hasse [4], Iwasawa [5]) gives an explicit formula for this map 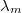 (encoding the Hilbert symbol on the
(encoding the Hilbert symbol on the  -th layer). To state their formulas, let
-th layer). To state their formulas, let ![$A=\mathbb{Z}_p[ [t-1]]$](./latex/ExplicitReciprocity/latex2png-ExplicitReciprocity_189640797_-5.gif) be the ring of formal power series in the variable
be the ring of formal power series in the variable  . The ring homomorphism
. The ring homomorphism 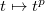 presents
presents 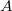 as a free
as a free 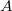 -module of rank
-module of rank 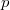 and induces a norm map
and induces a norm map 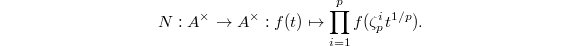
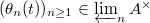 be a norm compatible sequence of
be a norm compatible sequence of 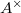 . Then
. Then 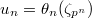 form a norm compatible sequence in
form a norm compatible sequence in 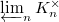 , and
, and 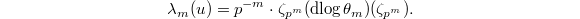
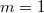 , we recover Kummer's formula by taking
, we recover Kummer's formula by taking 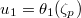 to be
to be 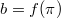 and obtain that
and obtain that 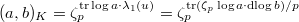 . Notice this formula is valid for general units and does not involve any particular cyclotomic units yet.
. Notice this formula is valid for general units and does not involve any particular cyclotomic units yet.
 -functions — in this case — partial Riemann zeta functions
-functions — in this case — partial Riemann zeta functions  ), we choose the norm compatible elements
), we choose the norm compatible elements 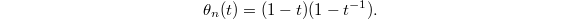 So that
So that 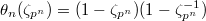 . Since
. Since 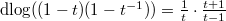 , we obtain
, we obtain 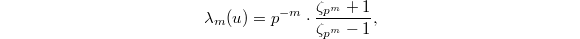 where the cyclotomic units show up!
where the cyclotomic units show up!
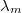 can be essentially viewed as (after identifying the terms with their duals using the Hilbert symbol)
can be essentially viewed as (after identifying the terms with their duals using the Hilbert symbol)
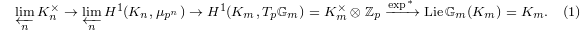 Notice the first map is nothing but the connecting homomorphism in Kummer theory and the last map is nothing but the Block—Kato dual exponential map for the
Notice the first map is nothing but the connecting homomorphism in Kummer theory and the last map is nothing but the Block—Kato dual exponential map for the 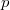 -adic Galois representation
-adic Galois representation 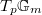 .
.
- Differential forms are more explicit than Galois cohomology. To switch to the former, one composes the etale Abel—Jacobi map with the dual exponential map.
- After choosing an explicit norm compatible sequence, the explicit reciprocity law connects explicit classes in Galois cohomology with special values of
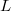 -functions.
-functions.
Needless to say, the first step (though purely local) is by no means easy. The second step (constructing Euler systems) is even harder! (but see a series of recent works of Bertolini—Darmon—Rotger and Kings/Lei—Loeffler—Zerbes on generalized Kato classes).
 Kato's explicit reciprocity laws
Kato's explicit reciprocity laws
Kato's explicit reciprocity law can be viewed as a generalization from the tower of cyclotomic fields 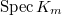 to the tower of open modular curves
to the tower of open modular curves 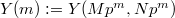 . Here we fix two positive integers
. Here we fix two positive integers 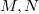 coprime to
coprime to 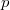 and
and 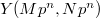 roughly parametrizes elliptic curves together with a marked
roughly parametrizes elliptic curves together with a marked 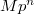 -torsion
-torsion 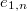 and a marked
and a marked 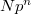 -torsion point
-torsion point 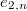 . Similarly define the tower of compact modular curves
. Similarly define the tower of compact modular curves 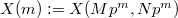 . One needs
. One needs 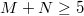 to avoid stacky issues but it is instructional to just think hypothetically as if
to avoid stacky issues but it is instructional to just think hypothetically as if 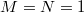 .
.
The map generalizing (1) is then given by
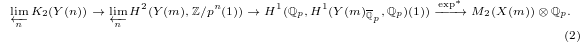
Here:
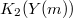 is the second
is the second 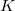 -group of the open modular curve
-group of the open modular curve 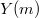 . Notice in the classical case
. Notice in the classical case 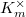 is the first
is the first 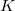 -group of
-group of 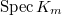 .
.- The first map is induced by composing the Chern class map (the etale regulator) together with cup product with
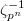 ,
, 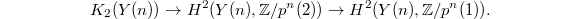
- The second map comes from Leray spectral sequence for
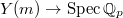 (so the first two maps together essentially gives the etale Abel-Jacobi map).
(so the first two maps together essentially gives the etale Abel-Jacobi map). - The third map is the Bloch—Kato dual exponential map
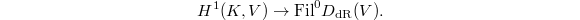 For
For 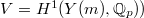 , we have
, we have 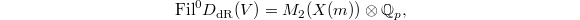 where
where 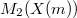 is the space of weight 2 modular forms on
is the space of weight 2 modular forms on 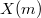 .
.
Kato's explicit reciprocity law ([1, Prop. 10.10]) says

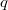 -expansions
-expansions
To prove Kato's explicit reciprocity law, one uses the 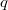 -expansion principle (a modular form is determined by its
-expansion principle (a modular form is determined by its 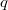 -expansion). More precisely:
-expansion). More precisely:
- Consider
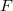 , the
, the 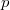 -adic completion of the function field of the modular curve of level
-adic completion of the function field of the modular curve of level 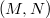 at a cusp. It is a complete discrete valuation field of characteristic 0 with valuation ring
at a cusp. It is a complete discrete valuation field of characteristic 0 with valuation ring ![$$\mathcal{O}_F=\varprojlim_n (\mathbb{Z}[\zeta_N]_\mathfrak{p}[ [q^{1/M}]][q^{-1}]/p^n$$](./latex/ExplicitReciprocity/latex2png-ExplicitReciprocity_182091164_.gif) and imperfect residue field
and imperfect residue field 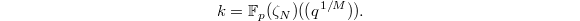 One can visualize
One can visualize 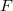 as a "2-dimensional local field" (geometrically a puncture disk around the cusp). Imagine if
as a "2-dimensional local field" (geometrically a puncture disk around the cusp). Imagine if 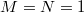 , then
, then 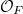 is just the
is just the 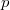 -adic completion of
-adic completion of ![$\mathbb{Z}_p[ [q]][q^{-1}]$](./latex/ExplicitReciprocity/latex2png-ExplicitReciprocity_149328220_-5.gif) and
and 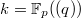 .
. - Let
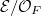 be the Tate curve
be the Tate curve ![$\mathcal{E}/\mathbb{Z}[ [q]]$](./latex/ExplicitReciprocity/latex2png-ExplicitReciprocity_9287371_-5.gif) base changed to
base changed to 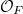 . Notice that
. Notice that 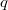 is invertible, so
is invertible, so 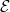 is indeed an elliptic curve.
is indeed an elliptic curve. - Let
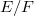 be its generic fiber.
be its generic fiber. - The triple
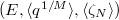 defines an
defines an 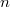 -point of
-point of 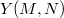 , denoted by
, denoted by 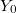 .
. - Let
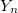 be the pullback
be the pullback 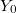 along the natural projection
along the natural projection 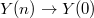 . These cusps
. These cusps 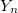 of
of 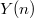 form a Galois covering of the cusp
form a Galois covering of the cusp 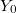 of
of 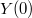 with Galois group
with Galois group 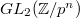 .
.
Analogous to (2), we obtain the map around the cusps, 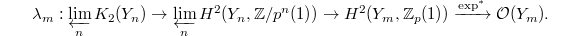 Here the construction of
Here the construction of 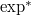 is not so easy and needs
is not so easy and needs 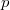 -adic Hodge theory over imperfect residual fields. For this reason it is a nontrivial task to check the compatibility with the usual Bloch—Kato dual exponential map in (2), but this is done in [1, 11]. If we take this compatibility for granted, then it remains to compute the map
-adic Hodge theory over imperfect residual fields. For this reason it is a nontrivial task to check the compatibility with the usual Bloch—Kato dual exponential map in (2), but this is done in [1, 11]. If we take this compatibility for granted, then it remains to compute the map 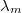 explicitly.
explicitly.
Now we make obvious changes to 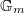 in the classical case:
in the classical case:
- The norm compatible functions will be on the
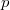 -divisible group
-divisible group 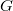 of
of 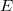 , instead of
, instead of 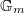 , and the multiplication
, and the multiplication 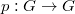 induces a norm map
induces a norm map 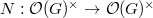 .
. - We evaluate these functions at the marked torsion points
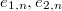 of
of 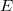 , instead of
, instead of 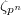 .
.
The main theorem of [2] (quoted as Prop. 10.12 in [1]) is the following.
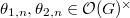 be two norm compatible sequences. Then
be two norm compatible sequences. Then 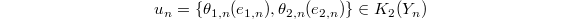 gives a norm compatible sequence
gives a norm compatible sequence 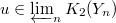 and
and 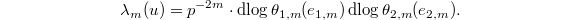 Here
Here 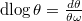 , where
, where 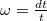 is the canonical basis of
is the canonical basis of 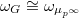 .
.
Using this theorem one can finally finish the proof of Theorem 3 by choosing specific norm compatible functions:
- Take
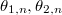 to be the theta functions
to be the theta functions 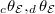 associated to
associated to 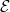 . These theta functions have product expansion roughly of the form (again imagine
. These theta functions have product expansion roughly of the form (again imagine 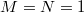 )
) 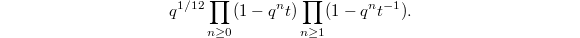 This is analogous to the rational function
This is analogous to the rational function 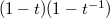 in the classical case.
in the classical case. - Using the product expansion one can explicitly evaluate their
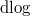 (along the vertical
(along the vertical 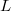 -direction rather than the horizontal
-direction rather than the horizontal 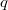 -direction) at the two marked torsion points
-direction) at the two marked torsion points 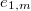 and
and 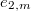 . This gives explicit Eisenstein series
. This gives explicit Eisenstein series 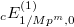 and
and 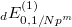 of weights
of weights 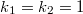 , which appear in the Rankin—Selberg integrals computing
, which appear in the Rankin—Selberg integrals computing 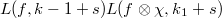 at
at 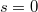 for forms
for forms 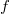 of weight
of weight 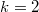 (so one gets the desired central value
(so one gets the desired central value 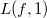 ). They are analogous to cyclotomic units in the classical case.
). They are analogous to cyclotomic units in the classical case.
References
[1]$p$-adic Hodge theory and values of zeta functions of modular forms, Astérisque (2004), no.295, ix, 117--290.
[2]Generalized explicit reciprocity laws, Adv. Stud. Contemp. Math. (Pusan) 1 (1999), 57--126.
[3]Ueber die Ergänzungssätze zu den allgemeinen Reciprocitätsgesetzen, J. Reine Angew. Math. 56 (1859), 270--279.
[4]Die beiden Ergänzungssätze zum reziprozitätsgesetz der $l^n$-ten potenzreste im körper der $l^n$-ten Einheitswurzeln, Abh. Math. Sem. Univ. Hamburg 6 (1928), no.1, 146--162.
[5]On explicit formulas for the norm residue symbol, J. Math. Soc. Japan 20 (1968), 151--165.
![$f\in \mathbb{Z}_p[ [ T]]$](./latex/ExplicitReciprocity/latex2png-ExplicitReciprocity_177837479_-5.gif) (though
(though 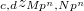 to
to 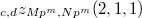 . Here
. Here
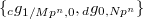 (the integer parameters
(the integer parameters 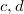 are needed for technical purposes);
are needed for technical purposes);