

Our first exam was held on Tuesday, September 29, in class.
The following charts show the distribution of scores, for each problem and the total. Each chart plots the scores for our class, with higher scores to the left, and perfect scores highlighted:
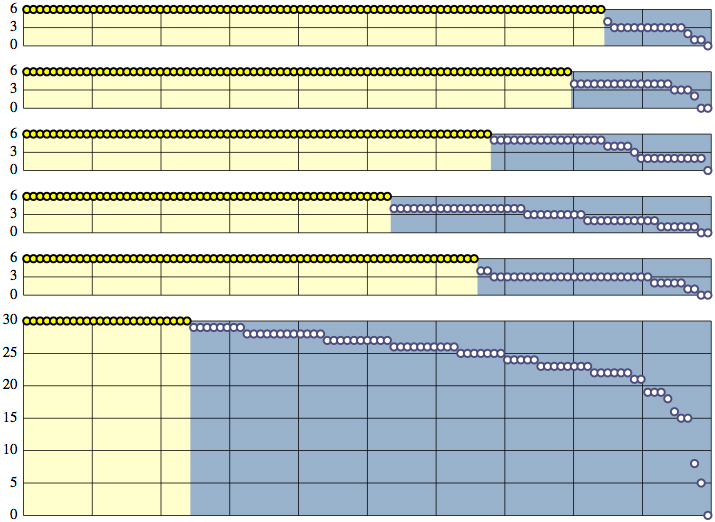
A grade report with a personalized version of these charts (your scores highlighted) is now in your CourseWorks dropbox.
I held a Linear Algebra problem session on Sunday, September 27, from 2:00 PM to 4:00 PM in Altschul 202 (Lehman Auditorium, Barnard).
For our first exam, you should be able to:
Chapters 1 and 2 of Bretscher are essential reading for the above material; work the early exercises after each section for additional practice. We have also been introducing ideas covered in greater detail in Chapter 3, which will also be relevant to our second exam.
The following Wikipedia pages may be useful:
In addition, various students have found Gilbert Strang’s video lectures on Linear Algebra to be very helpful. Start at the beginning:
Paths on graphs, and intersections of affice spaces, are covered in class but relegated to exercises in Bretscher. Your best bet is to study the selection below from our Linear Algebra Course Materials page, which includes worked solutions.
Our first problem set is due by the end of the day on Thursday, September 24. After this deadline, I will post solutions. Late work will not be accepted.
The following is a curated selection of practice materials from our Linear Algebra Course Materials page:
Ideally, one should get far more practice than these problem sets offer. Your best bet is to look at the course materials for previous semesters, many of which include solutions, and work as many similar problems as you can. Use your judgment in determining which past course materials are relevant:
The pattern in previous semesters has been for many students to submit a perfect first exam, and then do poorly on the second exam. This year’s first exam will be somewhat more difficult. In particular, students are expected to be able to generalize the above problem types to similar problems they have not seen before, which is possible if one understands how a particular method works. It is my responsibility to provide resistance to students who want to recognize standard problem types and apply a rote solution technique that they have learned for that problem type. To develop a more fluid understanding based on theory, try to avoid memorizing any details of how one solves the above problems. Rather, start each study session with a blank sheet of paper, and try to work out again from scratch how to solve these problems.
A personalized copy of our first assignment has been placed in your Courseworks Drop Box for this course. That copy includes a bar code identifying you and the problem, so that your work can be scanned, graded, and returned to you as a PDF file. Students prefer this system to rumaging weeks later through a cardboard box in the help room for their graded work, but this system requires some cooperation from you.
Please print this homework out on standard 8.5 x 11 printer paper, and submit it by the end of the day on Thursday, September 24. It may be handed in before or after class, or submitted via the homework boxes for our class, on the fourth floor of the Mathematics building, on the left as one walks toward my office, 426 Math. I will return your work to you as a scanned and graded PDF file.
Pen or pencil is fine, and colors are fine. Your writing needs to be dark enough to be legible when scanned; if it looks faint to you, don’t expect credit for what I cannot read. Please don’t use pencil that smudges easily, or leave eraser crumbs. Don’t crumble or fold your pages. Do not use alternate paper, such as three ring binder paper, other flimsy or oddly sized paper, or pages torn from a spiral notebook. If you disregard these guidelines, and I cannot scan your work, then your work will not be graded. Most students find these instructions easy, but some students ignore them, and I have to stop and clear a paper jam or clean the scanner. This is not the kind of attention you want!
If you print double-sided, then you can only use one side for the first problem; the second problem can continue onto additional blank paper. If you print single-sided, then you can continue your work on the back of each sheet, and then onto additional blank paper. The bar code must come first; anything that follows a bar code is assumed to be that problem, until my program sees the next bar code. If you use extra paper, flip through as a reader, and make sure that a bar code introduces each problem.
You don’t have to staple, but if you do I will cut off the staple with scissors, losing any work near the staple.
I am interested in experimenting with electronic submission, if you would like to return your homework via your Courseworks Drop Box. If you do so, provide scans of the same quality as my solutions above: 8.5 x 11, white or nearly white background, not twisted with respect to the page borders, and of sufficient resolution for your writing and the bar code to be clearly legible. You may submit PDF or JPG files, using file name(s) that start with the file name that you received, for example,
The above example was scanned in good light on a dark background, using my iPhone and the iOS app Scanner Pro 6, which does an excellent job of automatic cropping, alignment, and exposure control. I have tested that such scans can be used with my grading system. Please let me know if you have a similar app that you can recommend for Android phones.
Various copiers around campus can email you a scan of your work. It is tricky to train them to produce scans of an acceptable quality; they are optimized to decide where to put specks of black toner on laser paper, not to produce documents for viewing on a computer.
I scan using a Fujitsu iX500 sheet-fed scanner; I use it for nearly every sheet of paper that enters my life. Basic flatbed scanners start at $50, and more tediously do a credible job. Ordinary cell phone photos are acceptable for some purposes, but not for us. Do not return homework by email; I do not have an automated way to organize files received by email.
You may find it useful to consult study guides from previous semesters: