Groups and Symmetry Homework 1
Due Wednesday, September 20 in class
-
- Indicate whether each of the 5 shapes below is a
fundamental domain for the translations of the square grid.
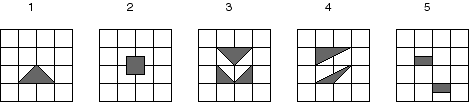
- Now, instead of allowing all the translations of the square
grid, we only allow translations up or down by any whole number
of units, translations left or right by any even number
of units or a combination of these moves. Decide whether each
of the 5 shapes is a fundamental domain for this set of
translations.
- Is it possible for a rectangle (four right angles) to be a
fundamental domain for the translations of the triangle grid? If
so, draw one on the triangle grid (you can use a photocopy of the
grid in your book to do your drawings). If not, why not?
- Pictured below is the equilateral triangle grid, and outlined
in red is the regular hexagon grid (6 equilateral triangles form 1
regular hexagon) superimposed on it. Draw arrows on the triangle
grid labeled a and b to represent translations so that every
translation of the triangle grid can be expressed as some integer
times a plus some integer times b. Now draw arrows on the triangle
grid labeled c and d to represent translations of the
hexagon grid so that every translation of the
hexagon grid can be expressed as some integer times c plus
some integer times d. What is the relationship of a and b to c and
d -- that is, write equations expressing c and d in terms of a and
b. You can do this problem on either a print of the picture below
or a photocopy of the triangle grid in your book (you'll have to
draw in the hexagon grid).

- When the "legal moves" for the square grid consist of all
translations, we can use one of the squares as a fundamental
domain. If we include all rotations of the square grid so that it
looks the same before and after the rotation in the "legal moves"
for the square grid, what can we now use for a fundamental domain?
Draw a fundamental domain for these legal moves on the grid below
or on a photocopy of the square grid from your book.



