These are my live-TeXed notes (reorganized according to my tastes) for the second part of the course Introduction to Riemann surfaces and Teichmuller theory by Professor Feng Luo, June 28 — July 14, at Math Science Center of Tsinghua University.
 Classification of Riemann Surfaces
Classification of Riemann Surfaces
Surfaces (assumed to be connected and orientable) of finite type (i.e., with finitely generated fundamental group) have a complete topological classification due to Mobius ([1, Theorem 1.1]):
- Any closed surface is homeomorphic to the connected sum of a sphere with
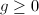 tori, where
tori, where 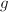 is called the genus.
is called the genus. - Any compact surface is obtained from a closed surface by removing
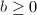 disjoint disks, where
disjoint disks, where 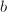 is the number of boundary components.
is the number of boundary components. - Any surface is obtained from a compact surface by removing
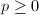 points from the interior, where
points from the interior, where 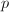 is the number of punctures.
is the number of punctures.
Among these, 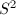 ,
, 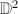 ,
, 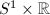 ,
, 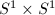 are the only cases with abelian fundamental group
are the only cases with abelian fundamental group 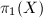 . However, each single topological class may contain various analytic structures.
. However, each single topological class may contain various analytic structures.
 be a topological surface. Denote by
be a topological surface. Denote by 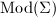 the set of biholomorphism classes of Riemann surfaces that are homeomorphic to
the set of biholomorphism classes of Riemann surfaces that are homeomorphic to 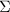 . This is called Riemann's moduli space.
. This is called Riemann's moduli space.
We can restate the uniformization theorem as follows.
Let  be a Riemann surface with nontrivial fundamental group. From general algebraic topology property, we know that there exists a simply connected surface
be a Riemann surface with nontrivial fundamental group. From general algebraic topology property, we know that there exists a simply connected surface 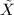 and a covering map
and a covering map 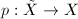 such that
such that 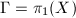 acts freely and discontinuously on
acts freely and discontinuously on 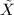 : for any
: for any 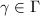 ,
, 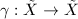 is a homeomorphism and
is a homeomorphism and 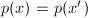 if and only if
if and only if 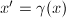 for some
for some 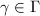 ; for any
; for any 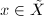 there exists a neighborhood
there exists a neighborhood 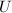 of
of  such that
such that 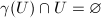 for any nontrivial
for any nontrivial  . In particular, for any nontrivial
. In particular, for any nontrivial  , we have
, we have 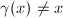 for any
for any 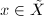 .
. 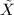 is a Riemann surface such that
is a Riemann surface such that 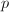 is analytic. The Uniformization Theorem tells us that
is analytic. The Uniformization Theorem tells us that  is either
is either  ,
, 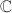 or
or 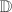 .
.
The main goal of this section is to prove the following classification of Riemann surfaces with simple topology.
 is a Riemann surface such that its fundamental group
is a Riemann surface such that its fundamental group 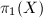 is abelian and nontrivial. Then
is abelian and nontrivial. Then
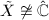 .
.- If
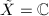 , then
, then 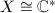 or
or 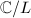 , where
, where 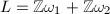 is a lattice in
is a lattice in 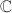 .
. - If
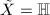 , then
, then 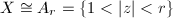 , the annulus of module
, the annulus of module 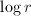 , where
, where 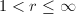 . Moreover,
. Moreover, 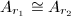 if and only if
if and only if 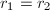 .
.
To prove Theorem 3, we need the following two lemmas.
- For any
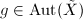 , we have
, we have 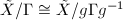 .
. - Any continuous map
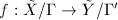 can be lifted to
can be lifted to 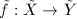 such that
such that 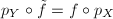 , where
, where 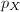 and
and 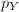 are the universal covering maps. Furthermore, if
are the universal covering maps. Furthermore, if  is a homeomorphism then
is a homeomorphism then 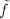 is so. Obviously, if
is so. Obviously, if  is analytic then
is analytic then 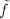 is so, hence if
is so, hence if 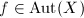 then
then 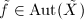 .
.
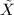 is simply connected and
is simply connected and 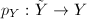 is a covering map, we choose
is a covering map, we choose 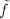 to be the lifting of
to be the lifting of 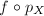 . Furthermore, suppose
. Furthermore, suppose  is a homeomorphism with
is a homeomorphism with 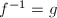 . Taking
. Taking 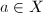 ,
, 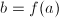 and a lift
and a lift 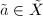 ,
, 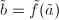 , we get a lifting
, we get a lifting 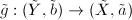 similarly. Then
similarly. Then 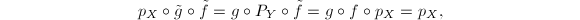 so
so 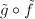 and
and 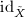 are both the liftings of
are both the liftings of  sending
sending 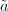 to
to 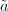 . The uniqueness of the lifting ensures that
. The uniqueness of the lifting ensures that 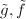 are inverses.
¡õ
are inverses.
¡õ
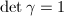 , the eigenvalues are of the form
, the eigenvalues are of the form 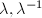 . The condition that the eigenvalues are real implies that
. The condition that the eigenvalues are real implies that 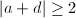 . The fixed points condition implies that
. The fixed points condition implies that 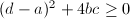 , namely
, namely 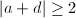 , too.
¡õ
, too.
¡õ
Now we are in a position to prove Theorem 3.
 has a fixed point in
has a fixed point in 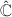 ,
, 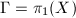 cannot act on
cannot act on 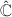 freely.
freely.
(b) Suppose 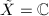 . The automorphism
. The automorphism 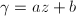 has no fixed points, hence
has no fixed points, hence 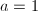 and
and  , namely
, namely 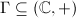 . If
. If 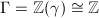 , then
, then 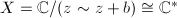 by
by 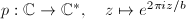 . If
. If 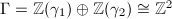 with
with 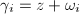 , then topologically
, then topologically  is
is 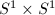 . We claim that
. We claim that 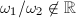 . If
. If 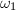 is a rational multiple of
is a rational multiple of 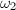 , then
, then 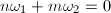 for
for 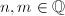 , therefore
, therefore 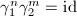 , which contradicts the fact that
, which contradicts the fact that 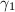 and
and 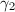 are generators of
are generators of 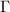 . If
. If 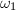 is an irrational multiple of
is an irrational multiple of 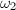 , then
, then 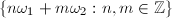 is dense in the line
is dense in the line 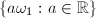 , so that
, so that 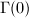 has limit points which contradicts the discontinuity. So
has limit points which contradicts the discontinuity. So 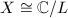 where
where 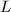 is a lattice. A similar argument shows that
is a lattice. A similar argument shows that 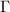 cannot have more than two generators.
cannot have more than two generators.
(c) Suppose 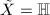 .
.
- If
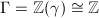 , with
, with 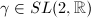 , then every fixed point of
, then every fixed point of  is inside
is inside 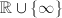 by freeness. After conjugating by some
by freeness. After conjugating by some 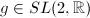 , we may assume that
, we may assume that  has the form
has the form 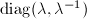 , where
, where 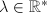 (by Lemma 2) or
(by Lemma 2) or 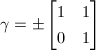 .
If
.
If 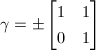 , then
, then 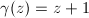 . So
. So 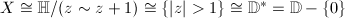 by
by 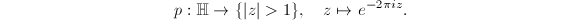 If
If 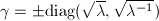 , then
, then 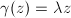 , where
, where 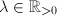 . Then
. Then 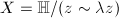 is biholomorphic to
is biholomorphic to 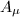 where
where 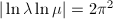 , by composing the logarithm map, the strip-scaling map and the exponential map
, by composing the logarithm map, the strip-scaling map and the exponential map 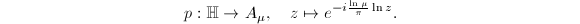
- If
 , then
, then  since
since  . Up to conjugation, we may assume that
. Up to conjugation, we may assume that 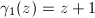 or
or 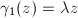 (
(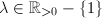 ). If
). If 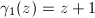 , then
, then 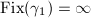 and
and 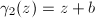 , so
, so  cannot act discontinuously; if
cannot act discontinuously; if  , then
, then 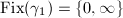 and
and 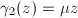 with
with 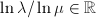 . If
. If 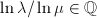 , then
, then 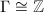 ; if
; if 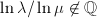 , then
, then 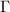 cannot act discontinuously.
cannot act discontinuously.
We claim that no two 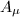 's are not biholomorphically equivalent. If
's are not biholomorphically equivalent. If 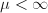 then
then 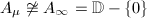 by Riemann's theorem on removable singularities. If
by Riemann's theorem on removable singularities. If 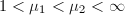 , suppose
, suppose 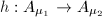 is a biholomorphism, then
is a biholomorphism, then 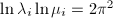 . By Lemma 1,
. By Lemma 1,  lifts to
lifts to  and
and 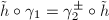 . Comparing the eigenvalues, we know
. Comparing the eigenvalues, we know 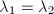 , therefore
, therefore 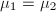 . The claim follows.
¡õ
. The claim follows.
¡õ
Now suppose 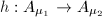 is a biholomorphism. Then by Caratheodory's Theorem 4,
is a biholomorphism. Then by Caratheodory's Theorem 4, 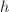 extends to a homeomorphism
extends to a homeomorphism 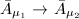 . Applying the Schwarz reflection theorem repeatedly, this map extends to a biholomorphism
. Applying the Schwarz reflection theorem repeatedly, this map extends to a biholomorphism 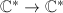 . Thus it is a scalar, which has to be 1 since
. Thus it is a scalar, which has to be 1 since 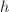 maps
maps 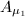 to
to 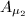 . So
. So 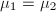 .
.
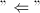 : by change of lattice basis and Remark 1.
: by change of lattice basis and Remark 1. 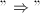 : composing
: composing 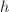 by an automorphism of
by an automorphism of 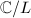 , we may assume
, we may assume ![$h[0]=[0]$](./latex/latex2png-Teichmuller_243782259_-5.gif) . Let
. Let 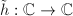 be the lifting of
be the lifting of 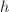 such that
such that 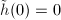 using Lemma 1. Hence
using Lemma 1. Hence 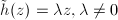 , which implies that
, which implies that 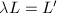 and
and 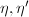 are equivalent under the action of
are equivalent under the action of 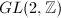 . Moreover,
. Moreover, 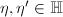 ensures that they are actually equivalent under
ensures that they are actually equivalent under 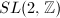 .
¡õ
.
¡õ
By now, we have completely described Riemann's moduli spaces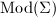 for all topological surfaces
for all topological surfaces 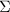 with abelian fundamental groups.
with abelian fundamental groups.
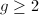 and
and 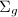 is a genus
is a genus 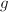 closed Riemann surface. Riemann computed that
closed Riemann surface. Riemann computed that 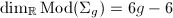 . To see that
. To see that 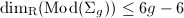 intuitively, let
intuitively, let ![$[X]\in \Mod(\Sigma_g)$](./latex/latex2png-Teichmuller_84046333_-5.gif) , then
, then 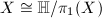 , where the fundamental group
, where the fundamental group 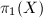 is generated by
is generated by 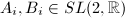 (
(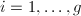 ) subject to
) subject to 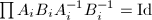 . The total number of degrees of freedom is
. The total number of degrees of freedom is 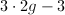 . Since
. Since 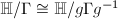 for
for 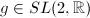 , the total dimension is no more than
, the total dimension is no more than  . More generally, let
. More generally, let 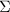 be a topological surface of finite type (homeomorphic to a compact space) such that
be a topological surface of finite type (homeomorphic to a compact space) such that 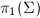 is generated by
is generated by 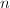 elements, then
elements, then 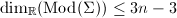 .
.
 Quasi-conformal maps
Quasi-conformal maps
We fix the following conventions in this section: 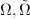 are open in
are open in 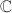 .
. 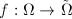 is a
is a 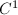 - smooth function. Denote
- smooth function. Denote 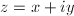 ,
, 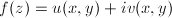 ,
, 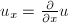 ,
, 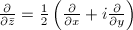 and so on. The following proposition can be thought of the chain rule with respect the variables
and so on. The following proposition can be thought of the chain rule with respect the variables  and
and 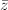 .
.
It is easy to see that every 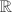 -linear map
-linear map 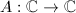 is given by
is given by 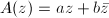 , where
, where 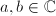 satisfies
satisfies 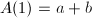 and
and 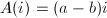 . Moreover,
. Moreover, 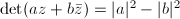 . If
. If 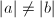 , then
, then 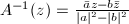 . It follows that the Jacobian of
. It follows that the Jacobian of  is equal to
is equal to 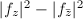 . So
. So  preserves orientation if and only if
preserves orientation if and only if 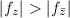 .
.
Geometrically, 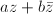 sends circles to ellipses. The following easy lemma describes which of the radii of a circle are sent to the axes of the corresponding ellipse.
sends circles to ellipses. The following easy lemma describes which of the radii of a circle are sent to the axes of the corresponding ellipse.
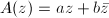 (assume that
(assume that 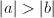 ), we have
), we have 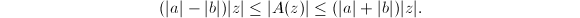 The second equality holds if and only if
The second equality holds if and only if 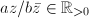 , if and only if
, if and only if 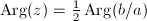 . The first equality holds if and only if
. The first equality holds if and only if 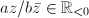 , if and only if
, if and only if 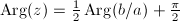 .
.
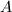 , denoted by
, denoted by 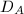 , is the ratio of axes of the ellipse
, is the ratio of axes of the ellipse 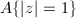 , which is equal to
, which is equal to 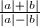 .
.
Note that 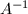 will switch the major axis and the minor axis. Also, it is easy to see that
will switch the major axis and the minor axis. Also, it is easy to see that 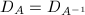 and
and 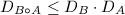 .
.
 preserves orientation. Define
preserves orientation. Define 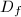 to be the dilatation of
to be the dilatation of 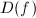 and
and 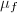 to be the Beltrami coefficient of
to be the Beltrami coefficient of 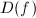 . Then
. Then 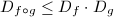 .
.
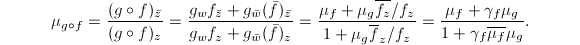 The lemma follows.
¡õ
The lemma follows.
¡õ
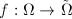 is a quasi-conformal map if
is a quasi-conformal map if  is an orientation-preserving homeomorphism,
is an orientation-preserving homeomorphism, 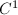 -smooth outside a discrete set
-smooth outside a discrete set 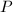 and there exists
and there exists 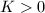 such that
such that 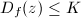 for any
for any 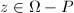 . Denote
. Denote 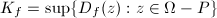 , then
, then 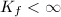 .
.
The concept of quasi-conformal maps can be generalized to Riemann surfaces using local coordinates. A natural question is to find the minimum dilatation quasi-conformal maps (in given a homotopy class) between Riemann surfaces with different analytic structures. This is the content of Teichmuller theory and the main theorem is the following.
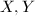 are compact Riemann surfaces of genus
are compact Riemann surfaces of genus 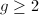 and
and 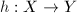 is a given homeomorphism. Then there exists a unique quasi-conformal map
is a given homeomorphism. Then there exists a unique quasi-conformal map 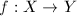 such that
such that  is homotopy equivalent to
is homotopy equivalent to 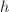 and
and 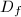 has the smallest dilatation among all such
has the smallest dilatation among all such  . Moreover,
. Moreover, 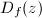 is a constant independent of
is a constant independent of  .
.
This theory is motivated by the classical Grotzsch problem.
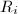 be rectangles with vertices
be rectangles with vertices 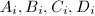 and size
and size 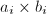 ,
, 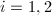 . Consider all
. Consider all 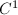 -smooth diffeomorphism
-smooth diffeomorphism 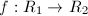 such that
such that 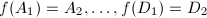 . We have:
. We have:
![$y\in[0, b_1]$](./latex/latex2png-Teichmuller_221554913_-5.gif) , let
, let 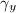 be the horizontal line segment
be the horizontal line segment 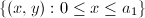 , then
, then 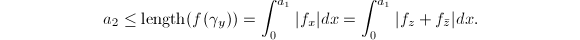 So using the triangle inequality, we obtain
So using the triangle inequality, we obtain 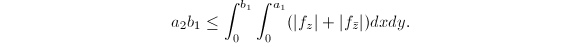 Now the Jacobian
Now the Jacobian 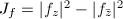 , so
, so
 by Cauchy's inequality. The equality holds if and only if
by Cauchy's inequality. The equality holds if and only if  is affine:
is affine: 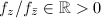 is a constant and
is a constant and 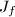 is a constant, therefore
is a constant, therefore 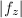 and
and 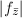 are constants. The theorem now follows.
¡õ
are constants. The theorem now follows.
¡õ
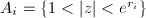 be an annulus of module
be an annulus of module 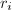 (
(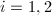 ). Then
). Then 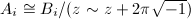 by
by 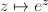 , where
, where 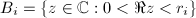 . So if
. So if ![$f:R_1=[0, r_1]\times [0, 2\pi]\rightarrow R_2=f(R_1)$](./latex/latex2png-Teichmuller_12340067_-5.gif) is a
is a 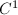 -smooth diffeomorphism, using the same proof as in Theorem 6, we know that
-smooth diffeomorphism, using the same proof as in Theorem 6, we know that 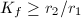 and the equality holds if and only if the lift
and the equality holds if and only if the lift 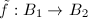 is affine given by
is affine given by  .
.
Teichmuller used quadratic differentials to solve this problem.
 Quadratic differentials
Quadratic differentials
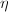 on
on 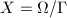 is an analytic function
is an analytic function 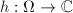 such that
such that 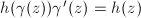 for any
for any 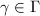 . Similarly, a quadratic differential
. Similarly, a quadratic differential 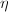 on
on 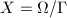 is an analytic function
is an analytic function 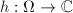 such that
such that 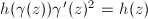 for any
for any 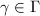 . More generally, for a Riemann surface
. More generally, for a Riemann surface  with analytic charts
with analytic charts 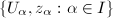 , a holomorphic 1-form on
, a holomorphic 1-form on  is a collection of analytic functions
is a collection of analytic functions 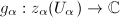 such that
such that 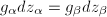 , i.e.,
, i.e., 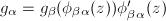 . Similarly, a quadratic differential on
. Similarly, a quadratic differential on  is a collection of analytic functions such that
is a collection of analytic functions such that 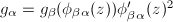 .
.
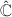 (
( ). All holomorphic 1-forms and quadratic differentials on
). All holomorphic 1-forms and quadratic differentials on 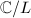 are of the forms
are of the forms 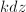 and
and 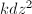 where
where 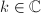 (
(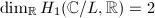 ).
).
 be a compact Riemann surface of genus
be a compact Riemann surface of genus 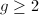 , then the vector space
, then the vector space 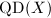 of all quadratic differentials on
of all quadratic differentials on  is of complex dimension
is of complex dimension 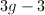 (and real dimension
(and real dimension  ).
).
Roughly speaking, we will see a correspondence between 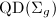 and
and 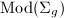 , which explains the significance of quadratic differentials in Teichmuller's construction (cf. Remark 4and Theorem 14).
, which explains the significance of quadratic differentials in Teichmuller's construction (cf. Remark 4and Theorem 14).
A holomorphic 1-form at 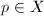 gives an
gives an 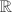 -linear map from the tangent space
-linear map from the tangent space 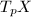 to
to 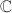 . Similarly, a quadratic differential
. Similarly, a quadratic differential 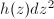 at
at 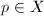 gives a quadratic form
gives a quadratic form ![$$B:v=[\alpha]\mapsto h(\alpha(t))\alpha'(t)^2|_{t=0}$$](./latex/latex2png-Teichmuller_33582089_.gif) from
from 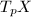 to
to 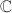 . A quadratic differential provides the following geometric data.
. A quadratic differential provides the following geometric data.
- A horizontal direction in
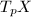 , namely
, namely 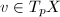 such that
such that 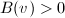 . So
. So 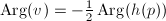 .
. - A vertical direction in
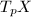 , namely
, namely 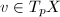 such that
such that 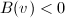 . So
. So 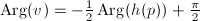 .
. - A flat Riemannian metric
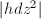 near
near 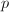 with
with 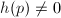 , given by
, given by 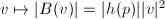 . This metric is conformal to the standard Euclidean metric, i.e., angles in
. This metric is conformal to the standard Euclidean metric, i.e., angles in 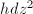 are the same as angles on the Riemann surface
are the same as angles on the Riemann surface  .
. 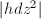 is locally isometric to the Euclidean space
is locally isometric to the Euclidean space 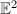 . Indeed, given
. Indeed, given 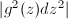 , define
, define 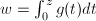 , then
, then 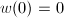 and
and 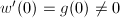 and
and 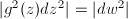 .
.
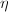 is a nonzero quadratic differential on a Riemann surface
is a nonzero quadratic differential on a Riemann surface  , then for any
, then for any 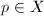 , there exists an analytic coordinate
, there exists an analytic coordinate 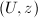 at
at 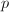 with
with 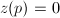 such that
such that 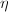 in
in 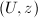 is given by
is given by 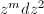 where
where 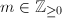 . We call this analytic coordinate the natural coordinate for
. We call this analytic coordinate the natural coordinate for 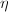 .
.
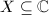 ,
, 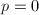 and
and 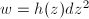 where
where 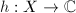 is analytic. If
is analytic. If 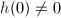 , we have just proved that
, we have just proved that  where
where 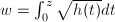 . Now suppose that
. Now suppose that 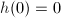 . Let
. Let 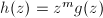 where
where 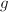 is analytic and
is analytic and 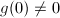 . Our goal is to write
. Our goal is to write 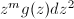 as
as 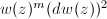 where
where  is analytic,
is analytic, 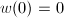 and
and 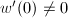 . Namely, we would like to solve the equation
. Namely, we would like to solve the equation 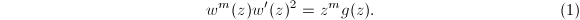 Formally, it is equivalent to
Formally, it is equivalent to 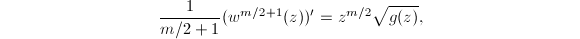 or
or 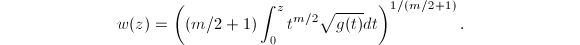 We need to justify that this is well-defined. Suppose
We need to justify that this is well-defined. Suppose 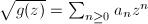 where
where 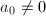 . Then
. Then 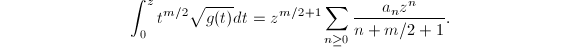 Hence
Hence 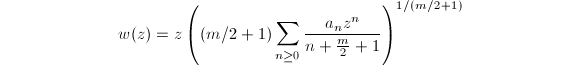 is single-valued and satisfies Equation 1.
¡õ
is single-valued and satisfies Equation 1.
¡õ
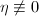 be a quadratic differential on a compact Riemann surface
be a quadratic differential on a compact Riemann surface  , then we obtain a flat Riemannian metric
, then we obtain a flat Riemannian metric  on
on  , so the area of
, so the area of 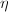 is well-defined:
is well-defined: 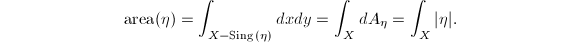 We also denote it by
We also denote it by 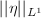 , then
, then 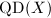 is a
is a 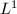 -normed vector space.
-normed vector space.
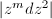 near
near 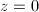 is a cone with cone angle
is a cone with cone angle 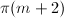 . The cone minus the vertex has a flat metric. Suppose the cone angle is
. The cone minus the vertex has a flat metric. Suppose the cone angle is 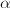 , then the pullback metric of
, then the pullback metric of  via
via 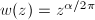 is
is 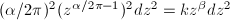 . For example, the metric
. For example, the metric 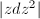 is obtained by gluing three half planes along the origin.
is obtained by gluing three half planes along the origin.
 Teichmuller Uniqueness Theorem
Teichmuller Uniqueness Theorem
Let  be a Riemann surface,
be a Riemann surface, 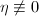 a quadratic differential on
a quadratic differential on  and
and 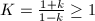 , where
, where 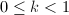 . Then there exists a new Riemann surface
. Then there exists a new Riemann surface  such that the underlying set of
such that the underlying set of  and
and  are the same, and there exists a quadratic differential
are the same, and there exists a quadratic differential 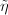 on
on  such that
such that 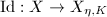 is
is 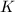 -quasi-conformal. Let us construct the analytic charts for
-quasi-conformal. Let us construct the analytic charts for  as follows. Pick any point
as follows. Pick any point 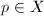 .
.
Type I 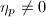 . By Theorem 8, there exists a natural coordinate
. By Theorem 8, there exists a natural coordinate 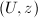 of
of 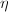 at
at 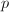 with
with 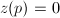 and
and 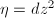 . Define a new analytic chart
. Define a new analytic chart 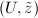 for
for  by
by 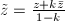 , in other words,
, in other words, 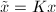 ,
, 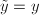 .
.
Note that if another 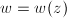 is analytic with
is analytic with 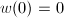 and
and 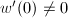 such that
such that 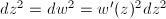 , then
, then 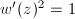 , which implies that
, which implies that 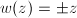 . So if
. So if 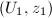 and
and 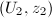 are two natural coordinates of Type I for
are two natural coordinates of Type I for 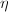 , the the transition function
, the the transition function 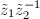 between them is analytic: we know that
between them is analytic: we know that 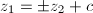 where
where  is a constant, therefore
is a constant, therefore 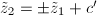 , so
, so 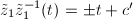 . Hence
. Hence 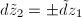 ,
, 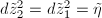 is a well-defined quadratic differential on
is a well-defined quadratic differential on 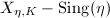 .
.
Type II 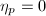 . Choose a natural coordinate
. Choose a natural coordinate  at
at  such that
such that 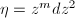 by Theorem 8. Define a chart for
by Theorem 8. Define a chart for  by
by 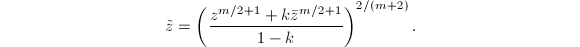 This is well-defined since the right hand side is
This is well-defined since the right hand side is 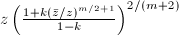 and
and 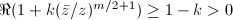 , so we can just choose the principal branch. Moreover,
, so we can just choose the principal branch. Moreover, 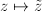 is a homeomorphism
is a homeomorphism 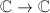 . Indeed,
. Indeed, 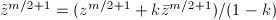 , so
, so 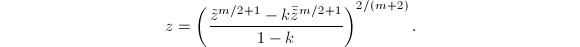
We claim that the transition function 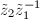 for a Type I chart
for a Type I chart 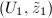 and a Type II chart
and a Type II chart 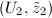 is analytic. Suppose
is analytic. Suppose 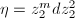 at
at 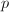 . We may assume that
. We may assume that 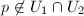 . Then we find that
. Then we find that 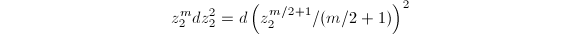 in
in 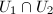 , so
, so 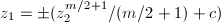 . Hence
. Hence 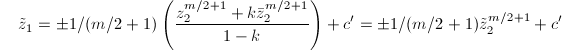 is analytic and
is analytic and 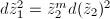 .
.
The following uniqueness theorem can be regarded as the general answer to the Grotzsch problem.
 be a compact Riemann surface with a nonzero quadratic differential
be a compact Riemann surface with a nonzero quadratic differential  . Let
. Let  be the new Riemann surface. If
be the new Riemann surface. If 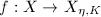 is a quasi-conformal map homotopic to the identity map, then
is a quasi-conformal map homotopic to the identity map, then 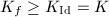 and the equality holds if and only if
and the equality holds if and only if 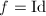 .
.
Denote 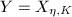 for simplicity.
for simplicity.
![$\alpha:[0,1]\rightarrow Y$](./latex/latex2png-Teichmuller_116178443_-5.gif) is an embedded horizontal arc in
is an embedded horizontal arc in 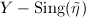 and
and ![$\tilde\alpha:[0,1]\rightarrow Y$](./latex/latex2png-Teichmuller_156900614_-5.gif) such that
such that 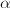 ,
, 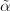 are homotopic relative to
are homotopic relative to 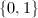 . Then the length of
. Then the length of 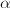 is no greater than the length of
is no greater than the length of 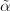 in
in  .
.
The problem occurs due to the presence of singularities (negative curvatures). To prove this Key Lemma, we need the following version of Gauss-Bonnet Theorem.
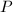 be a polyhedral surface obtained by isometric gluing of Euclidean triangles. For a vertex
be a polyhedral surface obtained by isometric gluing of Euclidean triangles. For a vertex  of
of 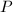 , define its curvature
, define its curvature 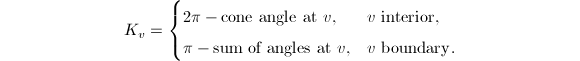 Then
Then 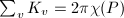 .
.
 . We may assume that
. We may assume that  is a piece-wise geodesic path homotopic to
is a piece-wise geodesic path homotopic to 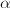 such that the vertices of
such that the vertices of 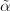 are in
are in 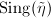 . Moreover, any vertex other than
. Moreover, any vertex other than 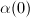 and
and 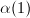 has cone angle at least
has cone angle at least 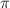 (otherwise we can decrease the length), so
(otherwise we can decrease the length), so 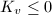 for these vertices. Now by the Gauss-Bonnet Theorem, we get
for these vertices. Now by the Gauss-Bonnet Theorem, we get 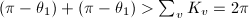 , impossible unless
, impossible unless 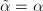 .
¡õ
.
¡õ
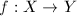 be a
be a 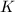 -quasi-conformal map homotopic to the identity map. Then there exists a constant
-quasi-conformal map homotopic to the identity map. Then there exists a constant 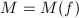 such that for any horizontal arc
such that for any horizontal arc 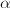 in
in 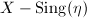 , we have
, we have 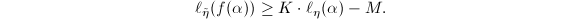
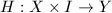 be a
be a 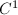 -smooth homotopy between
-smooth homotopy between 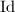 and
and  . Let
. Let 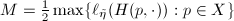 . Using Key Lemma 7, since
. Using Key Lemma 7, since 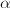 is also horizontal in
is also horizontal in 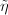 and
and 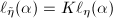 , we know that
, we know that 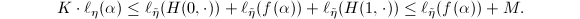 This completes the proof.
¡õ
This completes the proof.
¡õ
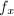 be the partial derivative with respect to the natural coordinate
be the partial derivative with respect to the natural coordinate 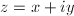 in
in 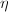 ,
, 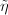 . Let
. Let 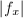 be measured in
be measured in 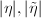 . Then
. Then 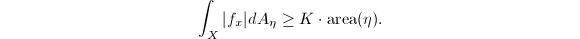
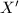 be
be  minus all horizontal lines through
minus all horizontal lines through 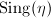 (several branches at one singular point), then
(several branches at one singular point), then 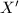 has full measure in
has full measure in  . For any
. For any 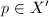 and
and 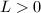 , define
, define 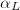 be the horizontal line centered at
be the horizontal line centered at 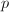 of length
of length 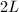 . Then
. Then 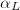 is simple since the horizontal direction is unique outside
is simple since the horizontal direction is unique outside 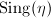 . We choose the arc length parametrization, namely
. We choose the arc length parametrization, namely 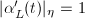 , so
, so 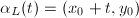 , where
, where 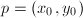 under the natural coordinate. Using Key Lemma 7, we know that
under the natural coordinate. Using Key Lemma 7, we know that 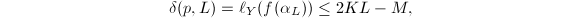 where
where 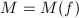 is a constant. But by the chain rule
is a constant. But by the chain rule 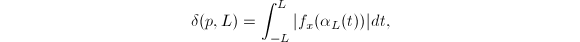 we know that
we know that 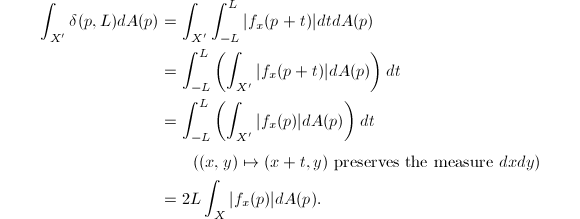 So
So 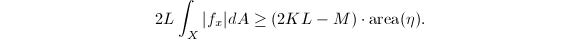 The lemma then follows by letting
The lemma then follows by letting 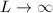 .
¡õ
.
¡õ
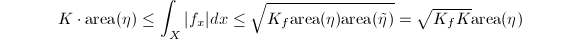 since
since  when
when  is compact. The theorem follows.
¡õ
is compact. The theorem follows.
¡õ
 Teichmuller spaces
Teichmuller spaces
Let us return to the study of Riemann's moduli space 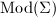 consisting of all Riemann surfaces
consisting of all Riemann surfaces  homeomorphic to a fixed topological surface
homeomorphic to a fixed topological surface 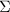 . We observe that it is the equivalent to study all complex structures on
. We observe that it is the equivalent to study all complex structures on 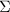 .
.
 Let
Let 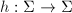 be a homeomorphism, then we can pull
be a homeomorphism, then we can pull 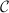 back to another complex structure
back to another complex structure 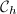 on
on 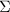 . Define
. Define  Then the Riemann moduli space
Then the Riemann moduli space 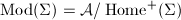 .
.
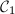 and
and 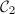 are Teichmuller equivalent if there is a biholomorphism
are Teichmuller equivalent if there is a biholomorphism 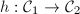 such that
such that 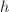 is homotopic to the identity map. The set of all Teichmuller classes is called the Teichmuller space, denoted by
is homotopic to the identity map. The set of all Teichmuller classes is called the Teichmuller space, denoted by 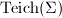 . Define
. Define 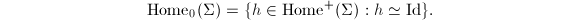 Then
Then 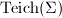 is the same as
is the same as 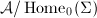 .
.
There is a subtle problem concerning "markings" on the Teichmuller space since we fix the underlying set 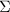 .
.
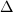 be a fixed triangle. Then
be a fixed triangle. Then 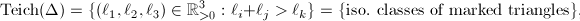 which is isomorphic to
which is isomorphic to 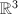 . But the Riemann moduli space
. But the Riemann moduli space 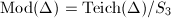 is isomorphic to
is isomorphic to 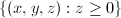 .
.
Instead of fixing the underlying set 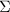 , we may consider the equivalence classes of marked Riemann surfaces.
, we may consider the equivalence classes of marked Riemann surfaces.
 . A marked Riemann surface
. A marked Riemann surface  by
by  is a pair
is a pair 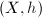 where
where 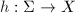 is a homeomorphism.
is a homeomorphism. 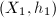 and
and 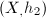 is Teichmuller equivalent if there exists a biholomorphism
is Teichmuller equivalent if there exists a biholomorphism 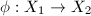 such that
such that 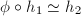 are homotopic. So the Teichmuller space
are homotopic. So the Teichmuller space 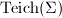 is the set of all Teichmuller equivalent classes of
is the set of all Teichmuller equivalent classes of 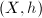 .
.
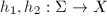 are homotopic, then
are homotopic, then 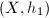 and
and 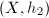 are Teichmuller equivalent, so we may replace
are Teichmuller equivalent, so we may replace 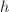 by its homotopy class.
by its homotopy class.
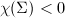 , then
, then 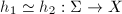 if and only if
if and only if 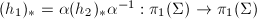 , where
, where 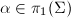 . This can be proved by looking at the universal covering
. This can be proved by looking at the universal covering 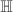 . So a marking on the Riemann surface
. So a marking on the Riemann surface 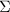 can be regarded as a choice of generators of the fundamental group
can be regarded as a choice of generators of the fundamental group 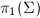 under the equivalence of conjugation.
under the equivalence of conjugation.
Our goal is to show that 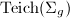 is isomorphic to the Fricke space
is isomorphic to the Fricke space 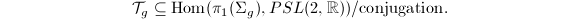 Fricke showed that
Fricke showed that  can be viewed as a subset in a
can be viewed as a subset in a  -dimensional manifold
-dimensional manifold 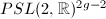 , and then one can prove that
, and then one can prove that  is actually homeomorphic to
is actually homeomorphic to 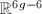 (cf. Uniformization Theorem 14).
(cf. Uniformization Theorem 14).
 Hyperbolic geometry
Hyperbolic geometry
This subsection is a crash course on the basics of hyperbolic geometry. Define a Riemannian metric 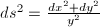 on
on 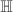 .
.
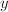 -axis is a geodesic in
-axis is a geodesic in 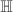 . Let
. Let 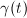 be a path in
be a path in 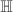 with staring point
with staring point 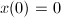 . Then
. Then 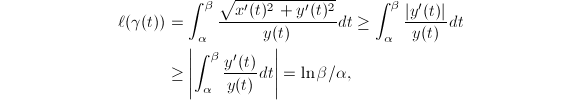 and equality holds if and only
and equality holds if and only 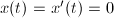 and
and 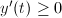 , if and only if
, if and only if 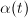 is along the
is along the 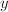 -axis.
-axis.
Note that 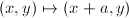 is an isometry of
is an isometry of 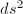 . Thus we know that all vertical lines are geodesics. Note that
. Thus we know that all vertical lines are geodesics. Note that 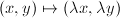 and
and 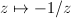 are also isometries. Since all Mobius transformations are composition of these three types of isometries, we know that
are also isometries. Since all Mobius transformations are composition of these three types of isometries, we know that 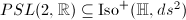 . Actually one can show that
. Actually one can show that 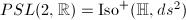 . Using the transformation
. Using the transformation 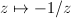 and the translations, it follows that all geodesics are either vertical lines or semicircles perpendicular to the
and the translations, it follows that all geodesics are either vertical lines or semicircles perpendicular to the  -axis.
-axis.
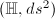 has constant Gaussian curvature
has constant Gaussian curvature 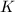 since
since 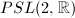 acts on
acts on 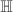 transitively. Indeed, for a Riemannian metric
transitively. Indeed, for a Riemannian metric 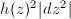 , the Gaussian curvature is given by
, the Gaussian curvature is given by 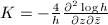 . A computation then shows that
. A computation then shows that 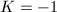 .
.
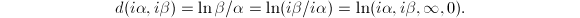 Since the cross ratio is invariant under a Mobius transformation, we have
Since the cross ratio is invariant under a Mobius transformation, we have 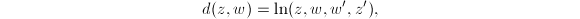 where
where 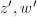 are the intersection points of the semicircle through
are the intersection points of the semicircle through 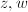 with the
with the  -axis.
-axis.
Let  be a compact Riemann surface of genus
be a compact Riemann surface of genus 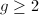 . The uniformization theorem tells us that
. The uniformization theorem tells us that 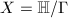 . The metric
. The metric 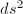 is invariant under
is invariant under 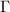 , so it induces a Riemannian metric
, so it induces a Riemannian metric 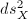 on
on  (thus such an
(thus such an  is called a hyperbolic surface) and now it makes sense to talk about lengths on
is called a hyperbolic surface) and now it makes sense to talk about lengths on  .
.
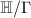 is a closed hyperbolic surface, then for
is a closed hyperbolic surface, then for 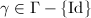 , we have
, we have  , or equivalently,
, or equivalently,  has two distinct real eigenvalues (which are called hyperbolic).
has two distinct real eigenvalues (which are called hyperbolic).
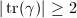 . If
. If 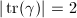 , after conjugation, we may assume that
, after conjugation, we may assume that 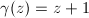 . Since
. Since  is compact, we can find finitely many small balls
is compact, we can find finitely many small balls  covering
covering  (so
(so  's are contractible). By Lebesgue's Lemma, there exists
's are contractible). By Lebesgue's Lemma, there exists 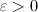 such that any loop of length less than
such that any loop of length less than  in
in  is in some
is in some 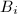 (hence homotopic to a point). But for
(hence homotopic to a point). But for 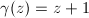 , consider the image of
, consider the image of 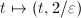 , whose length is
, whose length is 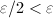 . It is homotopically nontrivial, a contradiction.
¡õ
. It is homotopically nontrivial, a contradiction.
¡õ
 Uniformization theorem
Uniformization theorem
We are now going to talk about the remaining two main theorems, namely the uniformization theorem and the measurable Riemann mapping theorem. Teichmuller asserted that the Teichmuller space 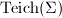 is isomorphic to
is isomorphic to 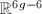 , but this result was not rigorously proved until the work of Ahlfors and Bers in 1950s. We will utilize some corollaries of the measurable Riemann mapping theorem (MRM) to prove the uniformization theorem in this section and discuss the MRM in the last section.
, but this result was not rigorously proved until the work of Ahlfors and Bers in 1950s. We will utilize some corollaries of the measurable Riemann mapping theorem (MRM) to prove the uniformization theorem in this section and discuss the MRM in the last section.
Let 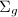 be a closed surface of genus
be a closed surface of genus 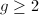 . Let
. Let 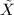 be the universal covering of
be the universal covering of  , then there exists a biholomorphism
, then there exists a biholomorphism 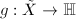 such that
such that 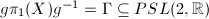 acts freely and discontinuously on
acts freely and discontinuously on 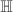 . Moreover,
. Moreover, 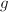 induces a biholomorphism on the quotient
induces a biholomorphism on the quotient 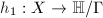 . In summary, we get a map
. In summary, we get a map
![\begin{align*}
\Psi:\Teich(\Sigma_g)&\rightarrow \mathcal{T}_g\subseteq\Hom(\pi_1(\Sigma_g),PSL(2,\mathbb{R}))/\text{conjugation}, \\ [(X,h)]&\mapsto (\phi:\gamma\mapsto g h_1(\gamma) g^{-1}).
\end{align*}](./latex/latex2png-Teichmuller_252314199_.gif) The image
The image  is called the Frick space of
is called the Frick space of 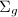 . By Remark 10 , the map
. By Remark 10 , the map 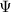 is injective. So we can identify
is injective. So we can identify 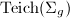 with
with  .
.
 has a natural topology induced from
has a natural topology induced from 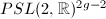 , hence we can use
, hence we can use 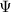 to define a topology on
to define a topology on 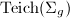 such that
such that 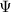 is a homeomorphism.
is a homeomorphism.
![$\pi_1(\Sigma_g)=\langle a_1, b_1,\ldots, a_g, b_g: [a_1, b_1]\cdots[a_g,b_g]=1\rangle$](./latex/latex2png-Teichmuller_246024894_-5.gif) . Let
. Let 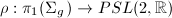 be a discrete faithful representation and
be a discrete faithful representation and 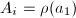 ,
, 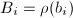 . We get
. We get ![\begin{equation*}
A_1B_1A_1^{-1}B_1^{-1}=[A_g, B_g]^{-1}\cdots [A_2, B_2]^{-1}. \tag{2}
\end{equation*}](./latex/latex2png-Teichmuller_47218397_.gif) After conjugation, we may assume that
After conjugation, we may assume that 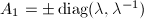 , where
, where 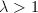 by Lemma 10. Suppose
by Lemma 10. Suppose 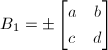 . By the proof of Theorem 3, we know
. By the proof of Theorem 3, we know 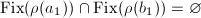 in
in 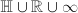 , since
, since 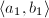 is nonabelian. But
is nonabelian. But 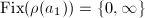 , so
, so 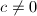 (consider
(consider  ) and
) and  (consider 0).
(consider 0).
Now 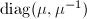 commutes with
commutes with 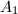 , so after conjugation we get
, so after conjugation we get 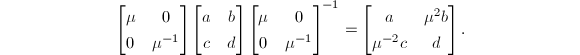
We may assume 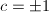 for
for 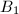 . If we can solve uniquely
. If we can solve uniquely 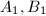 from Equation 2, then
from Equation 2, then 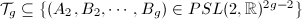 . Indeed, we compute that
. Indeed, we compute that 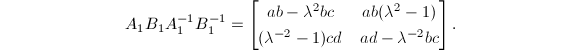 and one can show that
and one can show that 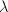 ,
, 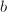 ,
,  ,
, 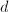 can be solved successively using the fact that
can be solved successively using the fact that 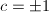 ,
,  .
¡õ
.
¡õ
By the Riemann-Roch Theorem 7, 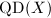 is a
is a  dimensional
dimensional 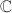 -vector space and has a natural
-vector space and has a natural 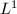 -norm. Let
-norm. Let 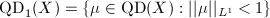 . Denote
. Denote 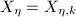 , where
, where 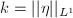 . Define the Teichmuller map
. Define the Teichmuller map ![$$\Phi: \QD_1(X)\rightarrow \Teich(\Sigma_g),\quad \eta\mapsto [X_\eta]=[(X_\eta,\Id)].$$](./latex/latex2png-Teichmuller_85191659_.gif)
Now the Teichmuller Uniqueness Theorem 9 can be restated as follows.
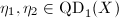 and
and ![$[(X_{\eta_1},\Id_1)]=[(X_{\eta_2},\Id_2)]$](./latex/latex2png-Teichmuller_118188258_-5.gif) , then there exists a biholomorphism
, then there exists a biholomorphism 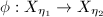 such that
such that 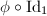 and
and 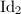 are homotopic. By the Teichmuller Uniqueness Theorem 9, we know that
are homotopic. By the Teichmuller Uniqueness Theorem 9, we know that 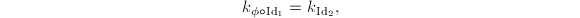 therefore
therefore 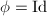 . It follows from the construction of
. It follows from the construction of 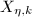 that
that 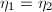 .
¡õ
.
¡õ
Combining Theorem 11 and Theorem 12, we obtain the following picture: ![$$\xymatrix{\QD_1(X) \ar@{^{(}->}[r]^-\Phi & \Teich (\Sigma_g) \ar[r]^-\Psi_-{\sim} & \mathcal{T}_g\subseteq M^{6g-6}.}$$](./latex/latex2png-Teichmuller_111308510_.gif)
The next two lemmas will be proved using MRM in the next section.
Now the uniformization theorem will follow easily from the above two lemmas and Brouwer's famous invariance of domain theorem.
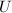 be an open set in
be an open set in 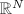 and
and 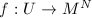 be a one-to-one continuous map into a manifold of the same dimension, then
be a one-to-one continuous map into a manifold of the same dimension, then  is open in
is open in 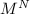 and
and 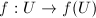 is a homeomorphism.
is a homeomorphism.
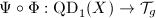 is a homeomorphism. In particular, the Teichmuller space
is a homeomorphism. In particular, the Teichmuller space 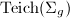 and the Fricke space
and the Fricke space  are homeomorphic to
are homeomorphic to 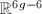 .
.
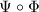 is open in
is open in  . By the properness in Lemma 11and the fact that the target
. By the properness in Lemma 11and the fact that the target  is a locally compact Hausdorff space, we find that
is a locally compact Hausdorff space, we find that 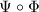 is a closed map and thus the image of
is a closed map and thus the image of 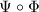 is also closed in
is also closed in  . But
. But  is connected by Lemma 12, hence the image of
is connected by Lemma 12, hence the image of 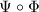 is the whole of
is the whole of  , which completes the proof.
¡õ
, which completes the proof.
¡õ
 Measurable Riemann Mapping Theorem
Measurable Riemann Mapping Theorem
As promised in the last section, we shall discuss the Measurable Riemann Mapping Theorem and utilize it to finish the proof of the uniformization theorem.
Let 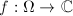 be a quasi-conformal map. By definition, the supremum norm of the Beltrami coefficients
be a quasi-conformal map. By definition, the supremum norm of the Beltrami coefficients 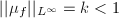 . The following inverse question asks about the existence of such quasi-conformal maps.
. The following inverse question asks about the existence of such quasi-conformal maps.
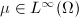 with
with 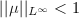 , is there any quasi-conformal map
, is there any quasi-conformal map  such that
such that  ?
?
The Measurable Riemann Mapping Theorem gives affirmative answers to this question.
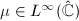 ,
, 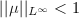 , then there exists a unique quasi-conformal map
, then there exists a unique quasi-conformal map 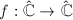 satisfying the normalization
satisfying the normalization 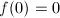 ,
,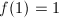 and
and 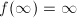 such that
such that  .
.
This deep theorem was proved by Lavrentev for 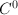 -functions
-functions 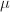 and by Morrey for measurable functions
and by Morrey for measurable functions 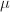 .
.
MRM can be also generalized to Riemann surfaces. From Sullivan's geometric point of view, the MRM simply says the following: place an ellipse on each tangent space on a Riemann surface, then there exists a unique quasi-conformal map sending this ellipse field to a circle field. In other words, for a pair 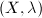 , we need to construct a new Riemann surface
, we need to construct a new Riemann surface 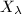 satisfying the above geometric condition.
satisfying the above geometric condition.
 are Riemann surfaces and
are Riemann surfaces and 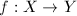 is a quasi-conformal map. Then the Beltrami differential (of
is a quasi-conformal map. Then the Beltrami differential (of  )
) 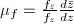 is well-defined on
is well-defined on  .
.
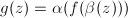 , where
, where  are analytic. Let
are analytic. Let 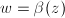 . By the chain rule, we have
. By the chain rule, we have  Then
Then 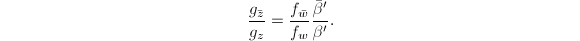 So
So 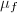 is well-defined.
¡õ
is well-defined.
¡õ
Now let 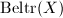 be the vector space of all Beltrami differentials on
be the vector space of all Beltrami differentials on  . It has a natural
. It has a natural 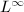 -norm given by
-norm given by 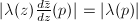 . We have a pairing
. We have a pairing 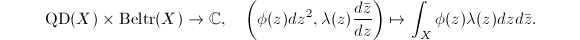 So
So 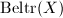 can be viewed as the dual of
can be viewed as the dual of 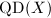 in some sense.
in some sense.
Looking at the universal covering and using the normal MRM Theorem 15, one can prove the following MRM on Riemann Surfaces.
 be a Riemann surface and
be a Riemann surface and 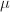 be a Beltrami differential on
be a Beltrami differential on  with
with 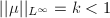 . Then there exists a Riemann surface
. Then there exists a Riemann surface 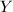 and a quasi-conformal map
and a quasi-conformal map  such that
such that 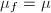 and
and  is unique up to biholomorphism.
is unique up to biholomorphism.
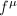 depends analytically on
depends analytically on 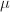 . This will imply that
. This will imply that 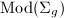 is a complex manifold (see [2]).
is a complex manifold (see [2]).
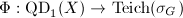 in terms of Beltrami differentials. For a quadratic differential
in terms of Beltrami differentials. For a quadratic differential 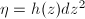 , the associated
, the associated 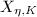 at
at  is constructed by stretching by a factor of
is constructed by stretching by a factor of 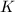 along the horizontal direction
along the horizontal direction 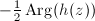 . On the other hand, we know that
. On the other hand, we know that 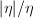 transforms as
transforms as 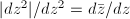 and thus it is a Beltrami differential. The quasi-conformal map
and thus it is a Beltrami differential. The quasi-conformal map 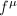 associated to the Beltrami differential
associated to the Beltrami differential 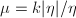 in Theorem 16satisfies
in Theorem 16satisfies 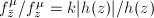 , hence it locally behaves as stretching by a factor of
, hence it locally behaves as stretching by a factor of 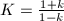 along the horizontal direction
along the horizontal direction 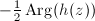 too. In summary, the Teichmuller map can be obtained by taking
too. In summary, the Teichmuller map can be obtained by taking 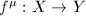 of the Beltrami differential
of the Beltrami differential 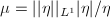 .
.
Finally, here comes the proof of Lemma 11 and Lemma 12, which in turn completes the proof of Theorem 14.
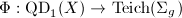 is the composition of the continuous MRM given by Theorem 16 and the continuous map
is the composition of the continuous MRM given by Theorem 16 and the continuous map 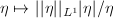 , hence continuous. If it is not proper, suppose
, hence continuous. If it is not proper, suppose 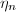 satisfies
satisfies 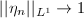 (
( ) and
) and 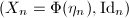 converges to
converges to 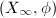 . Then we get quasi-conformal maps
. Then we get quasi-conformal maps 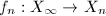 such that
such that  . But
. But 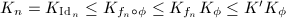 for some constant
for some constant 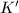 as
as 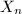 converges to
converges to 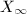 , which contradicts the assumption that
, which contradicts the assumption that  .
¡õ
.
¡õ
 is connected. Namely, we need to show that there is a continuous process from one
is connected. Namely, we need to show that there is a continuous process from one 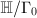 to another
to another  such that every matrix representation of
such that every matrix representation of  is discrete and faithful. This can be done by using
is discrete and faithful. This can be done by using  .
¡õ
.
¡õ
References
[1]A Primer on Mapping Class Groups, http://www.math.utah.edu/~margalit/primer/.
[2]Lectures on Quasiconformal Mappings (University Lecture Series), American Mathematical Society, 2006.
![$$\Mod(S^2)=\{[\hat{\mathbb{C}}]\},\quad \Mod(\mathbb{D}^2)=\{[\mathbb{C}], [\mathbb{D}]\}$$](./latex/latex2png-Teichmuller_64541091_.gif)
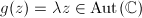 where
where 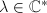 , then
, then 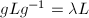 . By lemma
. By lemma 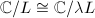 .
.
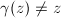 for any
for any 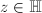 if and only if all eigenvalues of
if and only if all eigenvalues of 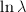 in the third case can be viewed as the length of the hyperbolic geodesic (cf. Example
in the third case can be viewed as the length of the hyperbolic geodesic (cf. Example 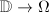 extends to a homeomorphism
extends to a homeomorphism 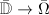 .
.
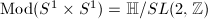 .
. ![$\Mod(S^1\times\mathbb{R})\cong
(1,\infty]$](./latex/latex2png-Teichmuller_96290683_-5.gif) where
where 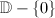 and
and 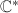 .
.
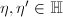 then
then 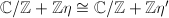 if and only if
if and only if  and
and 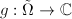 be
be 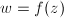 . Then
. Then
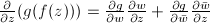 .
.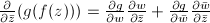 .
.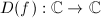 of
of 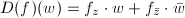 .
.
 The lemma follows.
The lemma follows.
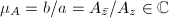 . We have
. We have 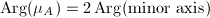 and
and 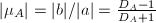 .
.
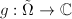 is
is 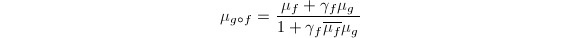 where
where 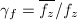 .
.
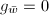 , then
, then 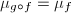 . If
. If  , then
, then 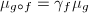 .
.
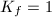 if and only if
if and only if 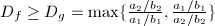 where
where  .
.
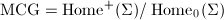 is called the mapping class group of
is called the mapping class group of  .
.
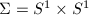 , then
, then 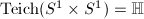 and
and 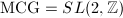 .
.
 is injective.
is injective.