The  -adic etale cohomology of algebraic varieties is much richer than their classical cohomology in the sense that it admits the action of Galois groups. In the 1960's, motivated by its relation to poles of zeta functions and a geometric analogue of the BSD conjecture, Tate was led to formulate his famous conjecture saying roughly that the
-adic etale cohomology of algebraic varieties is much richer than their classical cohomology in the sense that it admits the action of Galois groups. In the 1960's, motivated by its relation to poles of zeta functions and a geometric analogue of the BSD conjecture, Tate was led to formulate his famous conjecture saying roughly that the  -adic cohomology classes fixed by the Galois action should arise from algebraic cycles. Besides making the Tate conjecture precise, we will spend most of the time discussing Tate's original motivation, various evidence supporting it and a few surprising implications.
-adic cohomology classes fixed by the Galois action should arise from algebraic cycles. Besides making the Tate conjecture precise, we will spend most of the time discussing Tate's original motivation, various evidence supporting it and a few surprising implications.
This is an expanded note prepared for a STAGE talk at MIT, Spring 2013. Our main references are [1], [2], [3] and [4].
 The Tate conjecture
The Tate conjecture
Let 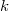 be a field and let
be a field and let 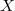 be a smooth geometrically irreducible projective variety over
be a smooth geometrically irreducible projective variety over 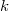 of dimension
of dimension 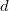 . We denote by
. We denote by 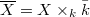 the base change of
the base change of 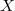 to the algebraic closure
to the algebraic closure 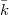 . The Galois group
. The Galois group 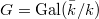 then acts on
then acts on 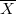 via the second factor.
via the second factor.
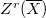 be the free abelian group generated by the irreducible closed subvarieties of
be the free abelian group generated by the irreducible closed subvarieties of 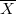 of codimension
of codimension  (
(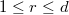 ). An element of
). An element of 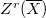 is called an algebraic cycle of codimension
is called an algebraic cycle of codimension  on
on 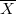 . Inside
. Inside 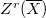 , we have a subgroup
, we have a subgroup 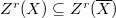 consisting of algebraic cycles that are defined over
consisting of algebraic cycles that are defined over 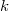 .
.
Let  be a prime different from
be a prime different from 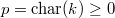 . Recall from John's talk that there is cycle class map (of
. Recall from John's talk that there is cycle class map (of  -modules)
-modules) 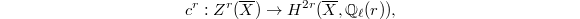 which associates to every algebraic cycle an
which associates to every algebraic cycle an  -adic etale cohomology class.
-adic etale cohomology class.
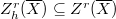 to be the kernel of
to be the kernel of 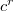 . These are the algebraic cycles
. These are the algebraic cycles  -adically homologically equivalent to zero. Denote the quotient group
-adically homologically equivalent to zero. Denote the quotient group 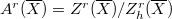 and its subgroup
and its subgroup 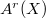 the image of
the image of 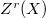 . Then
. Then 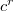 induces a map
induces a map
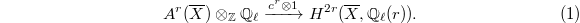 Notice that the image of
Notice that the image of 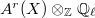 is fixed by the
is fixed by the 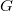 -action, so we have an induced map
-action, so we have an induced map
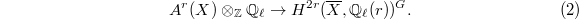 Our expectation will be that this is a bijection: the
Our expectation will be that this is a bijection: the 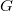 -fixed cohomology classes are exactly the
-fixed cohomology classes are exactly the 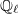 -span of the algebraic classes.
-span of the algebraic classes.
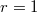 , the cycle class map
, the cycle class map 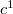 on divisors is relatively easier to describe. Taking the cohomology of the exact sequence of etale sheaves on
on divisors is relatively easier to describe. Taking the cohomology of the exact sequence of etale sheaves on 
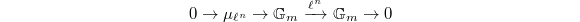 gives an injective map
gives an injective map 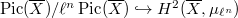 , which by passing to the limit induces the cycle class map for
, which by passing to the limit induces the cycle class map for  ,
, 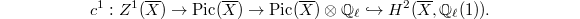 The kernel of
The kernel of 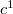 therefore consists of the torsion elements and elements that are
therefore consists of the torsion elements and elements that are 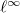 -divisible.
-divisible.
Notice the inclusions 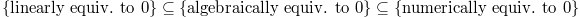 induces surjections
induces surjections 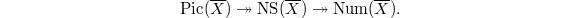 By the theorem of the base,
By the theorem of the base,  is a finitely generated abelian group. The kernel of the first surjection is a divisible group
is a finitely generated abelian group. The kernel of the first surjection is a divisible group 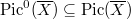 (points of the Picard variety) and the kernel of the second surjection is the torsion subgroup of
(points of the Picard variety) and the kernel of the second surjection is the torsion subgroup of 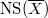 . So we have
. So we have 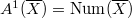 , a free abelian group of rank equal to the Picard number
, a free abelian group of rank equal to the Picard number 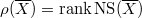 . In particular,
. In particular, 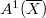 does not depend on the choice of
does not depend on the choice of  . It also follows that the map (2) is at least injective when
. It also follows that the map (2) is at least injective when 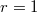 .
.
With this example in mind, we are now ready to state the famous Tate conjecture.
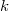 is finitely generated over its prime field.
is finitely generated over its prime field.
- (
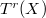 ) The map (2) is bijective.
) The map (2) is bijective. - (
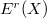 ) The
) The  -adically homological equivalence is the same as the numerical equivalence on
-adically homological equivalence is the same as the numerical equivalence on 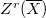 . In particular,
. In particular, 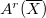 does not depend on the choice of
does not depend on the choice of  .
.
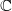 (or any algebraically closed field),
(or any algebraically closed field), 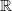 and
and 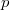 -adic fields are not finitely generated. The Tate conjecture is not expected to hold for the latter.
-adic fields are not finitely generated. The Tate conjecture is not expected to hold for the latter.
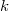 into
into 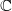 and appeal to the comparison theorem between
and appeal to the comparison theorem between  -adic etale cohomology and singular cohomology. Then the cycle class map
-adic etale cohomology and singular cohomology. Then the cycle class map 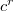 indeed factors through the finitely generated abelian group
indeed factors through the finitely generated abelian group 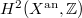 . It follows that
. It follows that 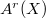 does not depend on the choice of
does not depend on the choice of  and the map (1) is injective, hence the injectivity of the map (2) follows immediately.
and the map (1) is injective, hence the injectivity of the map (2) follows immediately.
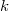 is a finite field, Tate proves that one can identify
is a finite field, Tate proves that one can identify 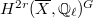 with
with 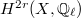 for any
for any 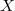 . The Kummer sequence on
. The Kummer sequence on 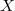 then gives an exact sequence
then gives an exact sequence 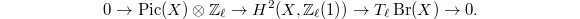 One sees that
One sees that 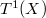 is true if and only if
is true if and only if 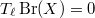 , i.e., the
, i.e., the  -primary part
-primary part ![$\Br(X)[\ell^\infty]$](./latex/latex2png-TateConjecture_211382433_-5.gif) is finite.
is finite.
 maps a 0-cycle to its degree, the Tate conjecture is trivial for
maps a 0-cycle to its degree, the Tate conjecture is trivial for 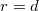 . In particular, for
. In particular, for 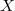 a curve, then Tate conjecture is trivially true; for
a curve, then Tate conjecture is trivially true; for 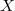 a surface, the only relevant conjecture is
a surface, the only relevant conjecture is 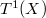 .
.
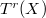 is insensitive to base field extension: if
is insensitive to base field extension: if 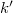 is a field extension, then
is a field extension, then 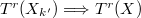 .
.
 Evidence
Evidence
Why should one believe the Tate conjecture? One should because it is a conjecture of Tate (proof by authority, QED). We are going to discuss two of Tate's major original motivations: one is the relation between 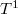 and the geometric analogue of the remarkable conjecture of Birch and Swinnerton-Dyer concerning the rational points of elliptic curves; one has to do with the following conjecture (now a theorem) on homomorphisms between abelian varieties.
and the geometric analogue of the remarkable conjecture of Birch and Swinnerton-Dyer concerning the rational points of elliptic curves; one has to do with the following conjecture (now a theorem) on homomorphisms between abelian varieties.
 )
Suppose
)
Suppose 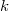 is finitely generated over its prime field. Let
is finitely generated over its prime field. Let 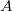 ,
, 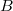 be two abelian varieties over
be two abelian varieties over 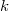 . Then the natural map
. Then the natural map 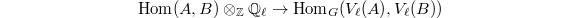 is bijective, where
is bijective, where 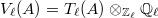 is the rational
is the rational  -adic Tate module of
-adic Tate module of 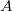 .
.
 -adic Galois representations) on the right hand side! It follows that two abelian varieties are isogenous if and only their Tate modules are isomorphic as
-adic Galois representations) on the right hand side! It follows that two abelian varieties are isogenous if and only their Tate modules are isomorphic as  -modules. For this reason the conjecture
-modules. For this reason the conjecture  is usually called Tate's isogeny conjecture.
is usually called Tate's isogeny conjecture.
 says that taking the Tate module is a fully faithful functor from an isogenous category of abelian varieties where the Hom sets are
says that taking the Tate module is a fully faithful functor from an isogenous category of abelian varieties where the Hom sets are 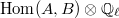 to the category of
to the category of  -adic
-adic 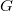 -representations. In the same spirit, the Tate conjecture implies that the functor from the category of pure motives over
-representations. In the same spirit, the Tate conjecture implies that the functor from the category of pure motives over 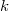 (defined using the numerical equivalence) to the category of
(defined using the numerical equivalence) to the category of  -adic
-adic 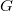 -representations given by taking
-representations given by taking  -adic etale cohomology is fully faithful.
-adic etale cohomology is fully faithful.
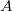 , one can show using the properties of the Weil pairing that
, one can show using the properties of the Weil pairing that 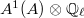 can be identified with the subset of elements of
can be identified with the subset of elements of 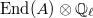 fixed under the Rosati involution ([5, I 14.2]). Similarly,
fixed under the Rosati involution ([5, I 14.2]). Similarly, 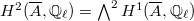 can be identified with the subset of elements of
can be identified with the subset of elements of 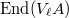 fixed under the Rosati involution. So
fixed under the Rosati involution. So 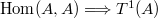 .
.
 was proved by Tate himself ([6]) soon after its formulation, now known as Tate's isogeny theorem. Zarhin [7] proved the case of function fields of positive characteristic. The number field case was proved by Faltings ([8]) as one of the steps in proving the Mordell conjecture. Faltings' method can be extended to any finitely generated fields.
was proved by Tate himself ([6]) soon after its formulation, now known as Tate's isogeny theorem. Zarhin [7] proved the case of function fields of positive characteristic. The number field case was proved by Faltings ([8]) as one of the steps in proving the Mordell conjecture. Faltings' method can be extended to any finitely generated fields.
The truth of  allows us to prove the following
allows us to prove the following
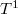 for the product
for the product 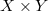 . On the one hand, the Kunneth formula gives decomposition
. On the one hand, the Kunneth formula gives decomposition
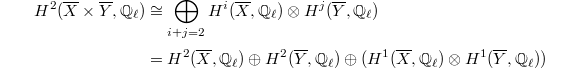 Notice that
Notice that 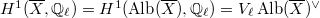 , where
, where 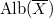 is the Albanese variety of
is the Albanese variety of 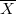 . So using the duality between
. So using the duality between 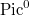 and
and 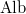 , we know that
, we know that 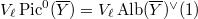 , hence
, hence
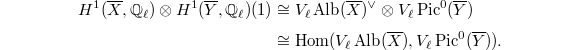 On the other hand, extending the base field if necessary (Remark 6), one can choose
On the other hand, extending the base field if necessary (Remark 6), one can choose 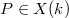 and
and 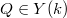 and obtain
and obtain 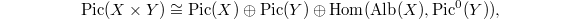 where
where 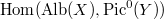 can be identified with the divisorial correspondence between
can be identified with the divisorial correspondence between 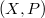 and
and 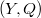 ([5, III 6.3]). This implies an isomorphism of free abelian groups
([5, III 6.3]). This implies an isomorphism of free abelian groups 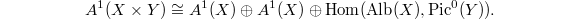 Now the assertion follows by comparing the two decompositions and the truth of
Now the assertion follows by comparing the two decompositions and the truth of  .
¡õ
.
¡õ
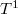 holds by taking products. In particular,
holds by taking products. In particular, 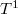 is true for the product of any number of curves and abelian varieties.
is true for the product of any number of curves and abelian varieties.
Even better, Tate proved that
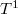 is birationally invariant. More generally, if there is a dominant rational map
is birationally invariant. More generally, if there is a dominant rational map 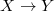 , then
, then 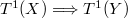 .
.
Together with the previous proposition, we see that 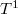 is true for any
is true for any 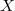 that is dominated by products of varieties for which
that is dominated by products of varieties for which 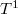 are known to be true.
are known to be true.
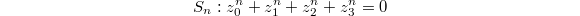 is dominated by the product of two curves
is dominated by the product of two curves 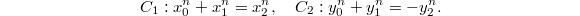 Explicitly,
Explicitly, ![$$C_1\times C_2 \rightarrow S,\quad ([x_0,x_1,x_2],[y_0,y_1,y_2])\mapsto[x_0y_2,x_1y_2,y_0x_2,y_1x_2].$$](./latex/latex2png-TateConjecture_145750861_.gif) So
So 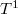 is true for every Fermat surface
is true for every Fermat surface 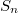 .
.
The Hodge conjecture is known for codimension 1 by Lefschetz 1-1 theorem. In contrast, 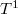 is still not known in general (and as you expected, even less is known when
is still not known in general (and as you expected, even less is known when 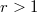 ). We list some known case about K3 surfaces (the theme of this seminar).
). We list some known case about K3 surfaces (the theme of this seminar).
Due to the work of many authors, 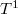 is also known to be true for Hilbert modular surfaces, quaternionic Shimura surfaces, Picard modular surfaces, Siegel modular threefolds... See the references in [2].
is also known to be true for Hilbert modular surfaces, quaternionic Shimura surfaces, Picard modular surfaces, Siegel modular threefolds... See the references in [2].
 Implications
Implications
There are many implications of the Tate conjecture. One surprising implication among them is the BSD conjecture for elliptic curves over global function fields. As we mentioned, this is one of Tate's original motivations for formulating 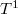 .
.
Assume now that 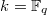 is a finite field of characteristic
is a finite field of characteristic 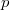 . Recall that the zeta function of
. Recall that the zeta function of 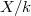 is defined to be the generating function of
is defined to be the generating function of 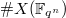 ,
, 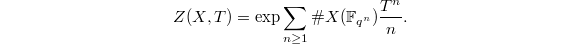 By the Lefschetz trace formula, this is in fact a rational function in
By the Lefschetz trace formula, this is in fact a rational function in 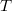 ,
, 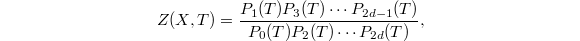 where here
where here 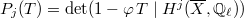 is the characteristic polynomial of the geometric Frobenius
is the characteristic polynomial of the geometric Frobenius 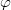 on
on 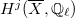 . By Deligne's proof of the Weil conjecture, this is a polynomial in
. By Deligne's proof of the Weil conjecture, this is a polynomial in ![$1+T \mathbb{Z}[T]$](./latex/latex2png-TateConjecture_18307586_-5.gif) independent of the choice of
independent of the choice of  . The inverse roots of
. The inverse roots of 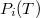 have all absolute values
have all absolute values 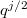 . For example,
. For example, 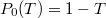 and
and 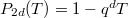 .
.
It follows that the poles of the zeta function 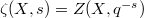 lie on the lines
lie on the lines 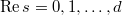 . In particular, the order of pole at
. In particular, the order of pole at 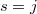 is exactly the multiplicity of
is exactly the multiplicity of 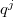 occurring as the eigenvalue of
occurring as the eigenvalue of 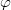 on
on 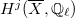 , or the multiplicity of
, or the multiplicity of  occurring as the eigenvalue of
occurring as the eigenvalue of 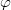 on
on 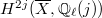 . If
. If 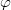 acts semisimply, this is exactly the dimension of
acts semisimply, this is exactly the dimension of 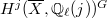 . In fact, by carefully doing linear algebra Tate showed that
. In fact, by carefully doing linear algebra Tate showed that
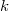 is a finite field. Then
is a finite field. Then 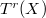 and
and 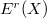 is true if and only if the order of pole of
is true if and only if the order of pole of 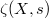 at
at  is equal to the rank of the group of codimension
is equal to the rank of the group of codimension  cycles on
cycles on 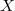 up to numerical equivalence. In particular,
up to numerical equivalence. In particular, 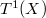 is true if and only the order of the pole of
is true if and only the order of the pole of 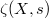 at
at 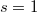 is equal to the the Picard number
is equal to the the Picard number 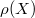 .
.
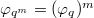 , the Tate conjecture implies that the rank of codimension
, the Tate conjecture implies that the rank of codimension  cycles on
cycles on 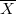 defined over
defined over 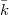 up to numerical equivalence is the number of roots of unity occurring as eigenvalues of
up to numerical equivalence is the number of roots of unity occurring as eigenvalues of 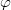 on
on 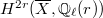 . Suppose
. Suppose 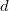 is even. By Poincare duality,
is even. By Poincare duality, 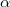 is an eigenvalue of
is an eigenvalue of 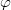 on the middle cohomology
on the middle cohomology 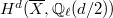 if and only if
if and only if 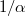 is. In other words, the number of such roots of of unity has the same parity as
is. In other words, the number of such roots of of unity has the same parity as  . In particular, when
. In particular, when 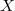 is a K3 surface,
is a K3 surface, 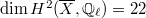 and
and 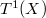 implies that the geometric Picard number
implies that the geometric Picard number 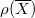 is always even!
is always even!
This may ring some bells if you have seen the remarkable conjecture of Birch and Swinnerton-Dyer, which predicts that the order of zero of the 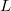 -function
-function 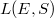 at
at 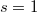 of an elliptic curve
of an elliptic curve 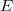 over a global field
over a global field 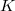 (more generally, any finitely generated field) is equal to the rank of the group of
(more generally, any finitely generated field) is equal to the rank of the group of 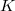 -rational points
-rational points 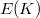 . When
. When 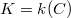 is the function field of a smooth projective curve
is the function field of a smooth projective curve 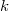 defined over
defined over 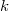 , by resolving singularities one can always find a regular projective elliptic surface
, by resolving singularities one can always find a regular projective elliptic surface 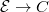 such that the generic fiber of
such that the generic fiber of 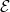 is
is 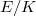 . If
. If 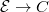 is smooth, the connection is extremely simple: on the one hand, unraveling the definition one finds that
is smooth, the connection is extremely simple: on the one hand, unraveling the definition one finds that 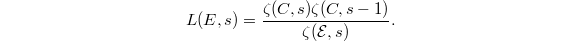 Since
Since 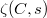 has simple poles at
has simple poles at 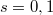 , it follows that at
, it follows that at 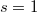 ,
, 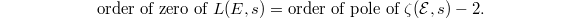 On the other hand,
On the other hand, 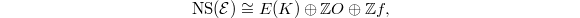 where
where 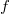 is the class of fibers and
is the class of fibers and 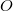 is the class of the zero section. Hence
is the class of the zero section. Hence 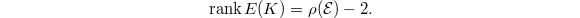 Therefore
Therefore 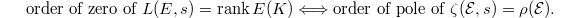 The left hand side is the BSD conjecture for
The left hand side is the BSD conjecture for 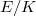 and by the previous theorem the right hand side is equivalent to the Tate conjecture for
and by the previous theorem the right hand side is equivalent to the Tate conjecture for 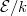 ! In general
! In general 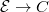 has singular fibers and the theorem of Shioda-Tate says that
has singular fibers and the theorem of Shioda-Tate says that 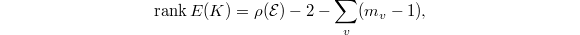 where
where 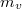 is the number of different components of the fiber over the closed point
is the number of different components of the fiber over the closed point  of
of 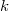 . When taking into account of the modification to
. When taking into account of the modification to 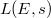 from bad places, the change of the order of zero at
from bad places, the change of the order of zero at 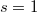 miraculously matches up with
miraculously matches up with 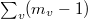 . Hence we know that
. Hence we know that
In view of Remark 4, one naturally wonders if the finiteness of the Brauer group of the elliptic surface 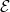 has anything to do the finiteness of the Shafarevich-Tate group
has anything to do the finiteness of the Shafarevich-Tate group 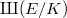 . Amazingly, Grothendieck [14] proved that
. Amazingly, Grothendieck [14] proved that
![$\Sha(E/K)[\ell^\infty]$](./latex/latex2png-TateConjecture_247602292_-5.gif) . This is what Artin and Swinnerton-Dyer actually proved in [9] for elliptic K3 surfaces.
. This is what Artin and Swinnerton-Dyer actually proved in [9] for elliptic K3 surfaces.
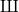 is finite. As Tate commented, otherwise "the Galois cohomology of an abelian variety should be a mess and the determination of the group of rational points by descent would be ineffective". In view of the above equivalence, why shouldn't one also believe the Tate conjecture (at least
is finite. As Tate commented, otherwise "the Galois cohomology of an abelian variety should be a mess and the determination of the group of rational points by descent would be ineffective". In view of the above equivalence, why shouldn't one also believe the Tate conjecture (at least 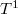 )?
)?
Finally it is worth mentioning another interesting implication of the Tate conjecture for K3 surfaces recently proved in [15].
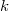 is a finite field of characteristic
is a finite field of characteristic 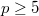 . Then
. Then 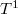 is true for all K3 surfaces over
is true for all K3 surfaces over 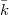 if and only there are only finitely many K3 surfaces defined over each finite extension of
if and only there are only finitely many K3 surfaces defined over each finite extension of 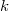 .
.
References
[1]Algebraic cycles and poles of zeta functions, Arithmetical Algebraic Geometry (Proc. Conf. Purdue Univ., 1963), Harper \& Row, 1965, 93--110.
[2]Conjectures on algebraic cycles in $l$-adic cohomology, Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., 55 Amer. Math. Soc., 1994, 71--83.
[3]Elliptic curves over function fields, Arithmetic of $L$-functions, IAS/Park City Math. Ser., 18 Amer. Math. Soc., 2011, 211--280.
[4]The Tate conjecture over finite fields (AIM talk), ArXiv e-prints (2007).
[5]Abelian Varieties (v2.00), Available at www.jmilne.org/math/.
[6]Endomorphisms of abelian varieties over finite fields, Invent. Math. 2 (1966), 134--144.
[7]Endomorphisms of Abelian varieties over fields of finite characteristic, Izv. Akad. Nauk SSSR Ser. Mat. 39 (1975), no.2, 272--277, 471.
[8]Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent. Math. 73 (1983), no.3, 349--366.
[9]The Shafarevich-Tate conjecture for pencils of elliptic curves on $K3$ surfaces, Invent. Math. 20 (1973), 249--266.
[10]Tate's conjecture for $K3$ surfaces of finite height, Ann. of Math. (2) 122 (1985), no.3, 461--507.
[11]Supersingular K3 surfaces for large primes, ArXiv e-prints (2012).
[12]The Tate conjecture for K3 surfaces over finite fields, ArXiv e-prints (2012).
[13]The Tate conjecture for K3 surfaces in odd characteristic, ArXiv e-prints (2013).
[14]Le groupe de Brauer. III. Exemples et compléments, Dix Exposés sur la Cohomologie des Schémas, North-Holland, 1968, 88--188.
[15]Finiteness of K3 surfaces and the Tate conjecture, ArXiv e-prints (2011).
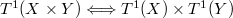 .
.
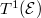 is equivalent to the BSD conjecture for
is equivalent to the BSD conjecture for 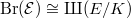 .
.