This is an introduction to a GIT construction of the moduli space of stable vector bundles on curves, presented at the GIT seminar. Our main sources are [1] and [2].
 Stable vector bundles on curves
Stable vector bundles on curves
Fix a smooth projective algebraic curve 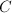 (over
(over 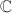 ) of genus
) of genus 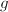 . Unlike the case of line bundles, it has been observed that in general all vector bundles are not classifiable. For example, one can construct a family of vector bundles of rank
. Unlike the case of line bundles, it has been observed that in general all vector bundles are not classifiable. For example, one can construct a family of vector bundles of rank 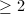 parametrized by the disk where all the fibers apart from the origin are mutually isomorphic, but not isomorphic to the fiber at the origin ([1, 11.32]). This "jump phenomenon" illustrates that the set of all vector bundles on curves is not even separated. In other words, even the coarse moduli space does not exist. To construct well-behaved moduli spaces of vector bundles, Mumford's geometric invariant theory hints at finding stable conditions on vector bundles and restricting our attention to stable vector bundles.
parametrized by the disk where all the fibers apart from the origin are mutually isomorphic, but not isomorphic to the fiber at the origin ([1, 11.32]). This "jump phenomenon" illustrates that the set of all vector bundles on curves is not even separated. In other words, even the coarse moduli space does not exist. To construct well-behaved moduli spaces of vector bundles, Mumford's geometric invariant theory hints at finding stable conditions on vector bundles and restricting our attention to stable vector bundles.
 is the ratio
is the ratio 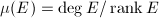 .
.  is called stable (resp. semistable) if every subbundle
is called stable (resp. semistable) if every subbundle 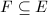 satisfies
satisfies 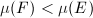 (resp.
(resp. 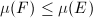 ). Equivalently,
). Equivalently,  is stable (resp. semistable) if every quotient bundle
is stable (resp. semistable) if every quotient bundle 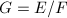 satisfies
satisfies 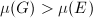 (resp.
(resp. 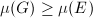 ).
).
By definition, every line bundle is stable. The following implications partially explain that why stable bundles are "nice".
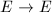 is an isomorphism, hence is a scalar by looking at one fiber.
¡õ
is an isomorphism, hence is a scalar by looking at one fiber.
¡õ
The moduli space 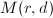 of stable vector bundles over
of stable vector bundles over 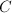 of rank
of rank  and degree
and degree 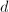 was first given by Mumford [3] and Seshadri [4]. Later, Gieseker gave a different construction which generalized to higher dimensions. Simpson invented a more natural and general method using Grothendieck's Quot scheme which also extends to singular curves and higher dimensions (see [5]).
was first given by Mumford [3] and Seshadri [4]. Later, Gieseker gave a different construction which generalized to higher dimensions. Simpson invented a more natural and general method using Grothendieck's Quot scheme which also extends to singular curves and higher dimensions (see [5]).
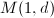 is simply the Picard variety
is simply the Picard variety 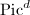 we have constructed. We have the natural map
we have constructed. We have the natural map 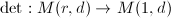 sending
sending  to its determinant bundle
to its determinant bundle 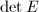 . We fix a line bundle
. We fix a line bundle 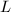 and study the fiber of this map. In other words, we are going to construct the space of stable vector bundles
and study the fiber of this map. In other words, we are going to construct the space of stable vector bundles 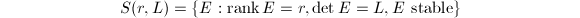 using GIT.
using GIT.
Similarly to the case of Picard varieties, we will assume 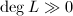 so that Riemann-Roch brings us some convenience.
so that Riemann-Roch brings us some convenience.
 has degree
has degree  . So there is no nonzero morphism
. So there is no nonzero morphism 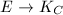 as
as 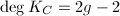 . Hence
. Hence 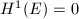 by Serre duality.
¡õ
by Serre duality.
¡õ
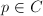 ,
, 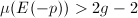 , we know that
, we know that 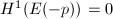 as
as 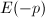 is semistable (tensoring with a line bundle does not change stability). By the exact sequence
is semistable (tensoring with a line bundle does not change stability). By the exact sequence 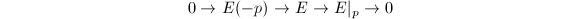 We know that
We know that 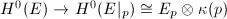 is surjective. By Nakayama's lemma we know that
is surjective. By Nakayama's lemma we know that 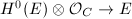 is surjective.
¡õ
is surjective.
¡õ
 Vector bundles of Rank 2
Vector bundles of Rank 2
Now let us concentrate on the case 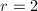 . Similarly to the case of Picard varieties, we will associate to each isomorphism class of vector bundles of rank 2 a
. Similarly to the case of Picard varieties, we will associate to each isomorphism class of vector bundles of rank 2 a 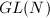 -orbit of a matrix and study its stability. Let
-orbit of a matrix and study its stability. Let  be a vector bundle of rank 2 with
be a vector bundle of rank 2 with 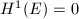 and generated by global sections. Let
and generated by global sections. Let 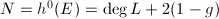 and
and 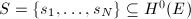 be a basis. Since
be a basis. Since  is generated by global sections, we have a surjection
is generated by global sections, we have a surjection 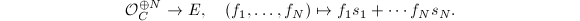 The pairing
The pairing 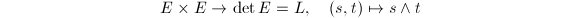 induces a map
induces a map 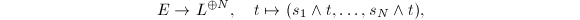 which is injective since
which is injective since  is generated by global sections. The composition map
is generated by global sections. The composition map 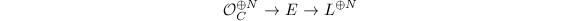 is given by the
is given by the  matrix
matrix 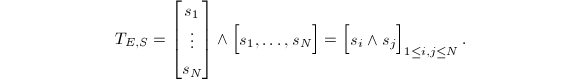 Let
Let 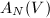 be the set of skew-symmetric
be the set of skew-symmetric 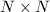 matrices with entries in a vector space
matrices with entries in a vector space 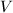 . Then
. Then 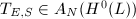 and we call it the Gieseker point of
and we call it the Gieseker point of 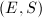 . The different choices of the marking
. The different choices of the marking 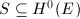 correspond to the
correspond to the 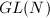 -orbit of
-orbit of 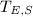 under the action
under the action 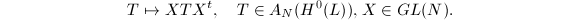 Moreover,
Moreover,  is isomorphic to the image of
is isomorphic to the image of 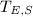 , hence one can recover
, hence one can recover  from its Gieseker points. So we have proved:
from its Gieseker points. So we have proved:
Since  is a vector bundle of rank 2, the matrix
is a vector bundle of rank 2, the matrix 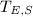 have rank 2 over the function field
have rank 2 over the function field  . Denote
. Denote 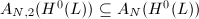 to be set of matrices having rank
to be set of matrices having rank 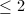 over
over 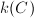 .
. 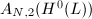 is a subvariety of
is a subvariety of 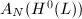 and the image of the above map
and the image of the above map 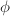 lies in it.
lies in it.
 Stability of Gieseker points
Stability of Gieseker points
To apply GIT to construct 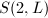 , we need to study the stability of
, we need to study the stability of 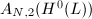 under the action of
under the action of 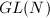 . This consists of two steps: for
. This consists of two steps: for 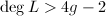 ,
,
Step 1 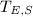 is semistable (stable) if and only if
is semistable (stable) if and only if  is semistable (stable).
is semistable (stable).
Step 2 Every semistable 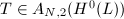 is the Gieseker point for some
is the Gieseker point for some  .
.
Assuming these two steps, we can construct 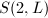 as a GIT quotient immediately.
as a GIT quotient immediately.
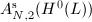 are free. Suppose
are free. Suppose 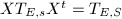 . We then have the following commutative diagram
. We then have the following commutative diagram ![$$\xymatrix{\mathcal{O}_C^{\oplus N}\ar[r]^{T_{E,S}} \ar[d]^{X^t}& L^{\oplus N} \\\mathcal{O}_C^{\oplus N}\ar[r]^{T_{E,S}} & L^{\oplus N}\ar[u]^{X} }$$](./latex/latex2png-StableVectorBundles_172428361_.gif) This gives an endomorphism of
This gives an endomorphism of  . Since
. Since  is stable, we know that
is stable, we know that  is simple. Hence
is simple. Hence 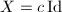 with
with 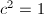 . Namely
. Namely 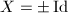 , which acts trivially on
, which acts trivially on 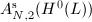 .
¡õ
.
¡õ
For the first step, we need the following observation. This phenomenon did not appear in the case of line bundles.
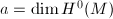 ,
, 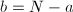 . We may assume
. We may assume 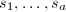 generates
generates  over
over  . Since
. Since 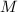 is a line bundle, we know
is a line bundle, we know 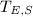 contains a top left
contains a top left 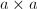 block consisting of only zeros. Write
block consisting of only zeros. Write 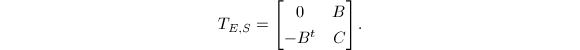 Consider a 1-parameter subgroup
Consider a 1-parameter subgroup 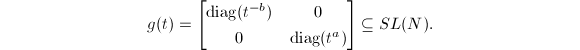 Then
Then 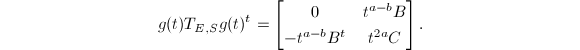 If
If 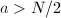 , then
, then 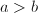 . Letting
. Letting 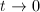 , we know
, we know 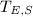 is unstable. If
is unstable. If 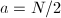 , then
, then 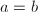 . Letting
. Letting 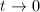 , we obtain the matrix
, we obtain the matrix 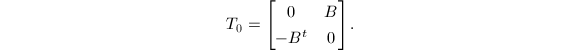
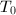 is not stable since it does not have finite stabilizer. So
is not stable since it does not have finite stabilizer. So 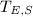 is not stable.
¡õ
is not stable.
¡õ
 be a vector bundle. We call
be a vector bundle. We call 
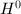 -semistable (resp.
-semistable (resp. 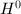 -stable) if
-stable) if 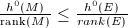 (resp.
(resp. 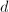 ) for any subbundle
) for any subbundle 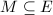 .
.
So we have shown:
In fact, the converse is also true:
We omit the proof of this fact since it is a bit long (see [1, 10.70]). The key idea is to construct 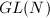 -semi-invariant polynomials using the Pfaffians or the radical vectors of skew symmetric matrices depending on whether
-semi-invariant polynomials using the Pfaffians or the radical vectors of skew symmetric matrices depending on whether 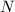 is even or odd.
is even or odd.
The condition for 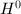 -semistability is already quite similar to semistability. One can use Riemann-Roch to prove the following, which finishes the proof of the first step.
-semistability is already quite similar to semistability. One can use Riemann-Roch to prove the following, which finishes the proof of the first step.
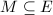 subbundle,
subbundle, 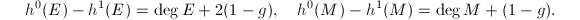 Since
Since  , we know that
, we know that 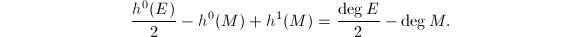 Since the left-hand-side is
Since the left-hand-side is 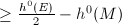 ,
, 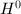 -(semi)stability implies (semi)stability. Now suppose
-(semi)stability implies (semi)stability. Now suppose 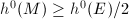 . Since
. Since 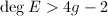 , we know that
, we know that 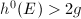 , hence
, hence 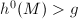 . Riemann-Roch implies that
. Riemann-Roch implies that 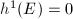 . Therefore
. Therefore 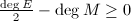 . The converse is proved.
¡õ
. The converse is proved.
¡õ
Now let us come to the second step.
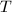 has only zeros in the first row and column. Then choosing the 1-parameter subgroup
has only zeros in the first row and column. Then choosing the 1-parameter subgroup 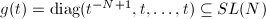 . Then
. Then 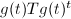 goes to 0 as
goes to 0 as 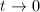 . Then
. Then 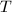 is unstable, a contradiction.
¡õ
is unstable, a contradiction.
¡õ
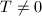 is skew-symmetric, it has even rank, so
is skew-symmetric, it has even rank, so 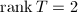 over
over 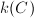 . Let
. Let  be the image of
be the image of 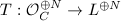 , then
, then  is a vector bundle of rank 2.
is a vector bundle of rank 2.
Let us first show 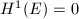 . Since
. Since 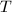 is semistable, we know that
is semistable, we know that 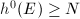 by the last lemma. Suppose
by the last lemma. Suppose 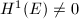 , then by Serre duality, we have a nonzero morphism
, then by Serre duality, we have a nonzero morphism 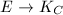 , which gives a map
, which gives a map 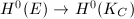 . Let
. Let 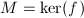 , then
, then 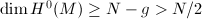 as
as 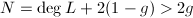 . So
. So 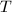 is unstable, a contradiction.
is unstable, a contradiction.
Next we need to show that 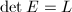 . The map
. The map 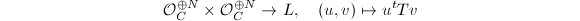 is skew-symmetric and vanishes on
is skew-symmetric and vanishes on 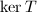 , hence induces a sheaf morphism
, hence induces a sheaf morphism 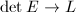 . From
. From 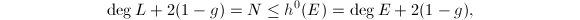 we know that
we know that 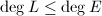 . So
. So 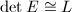 .
.
Finally we conclude  is semistable as
is semistable as 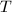 is the Gieseker point of
is the Gieseker point of  generated by global sections and
generated by global sections and 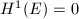 .
¡õ
.
¡õ
 , Gieseker similarly considered the action of
, Gieseker similarly considered the action of 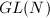 on the space
on the space 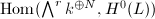 and deduced the stability condition.
and deduced the stability condition.
 Examples
Examples
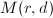 is smooth and if
is smooth and if 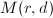 is nonempty (when
is nonempty (when 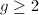 , or
, or 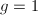 ,
, 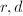 coprime, or
coprime, or 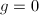 ,
, 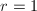 ), then
), then 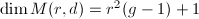 . Moreover,
. Moreover, 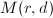 is a fine moduli space if and only if
is a fine moduli space if and only if 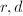 are coprime. The dimension of
are coprime. The dimension of 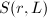 is
is 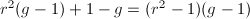 as expected. In particular,
as expected. In particular, 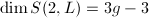 if it is nonempty.
if it is nonempty.
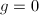 ,
, 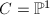 , Grothendieck's theorem asserts that each vector bundle on
, Grothendieck's theorem asserts that each vector bundle on 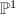 is a direct sum of line bundles. So there is no stable vector bundle of rank 2 and
is a direct sum of line bundles. So there is no stable vector bundle of rank 2 and 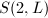 is empty.
is empty.
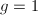 ,
, 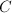 an elliptic curve, Atiyah's theorem asserts that for any line bundle
an elliptic curve, Atiyah's theorem asserts that for any line bundle 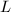 of odd degree, there exists a unique isomorphism class of stable vector bundles of rank 2 and
of odd degree, there exists a unique isomorphism class of stable vector bundles of rank 2 and 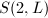 is a single point. For any line bundle
is a single point. For any line bundle 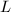 of even degree, there is no such stable bundle and
of even degree, there is no such stable bundle and 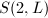 is empty.
is empty.
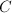 be a curve of genus
be a curve of genus 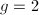 . Its canonical bundle
. Its canonical bundle 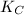 has degree 2. Take
has degree 2. Take 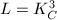 , then
, then 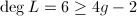 . By Riemann-Roch,
. By Riemann-Roch, 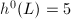 , so
, so 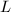 defines an embedding
defines an embedding 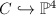 , whose image is the intersection of four quartics. A stable bundle
, whose image is the intersection of four quartics. A stable bundle  has
has 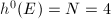 . An element of
. An element of 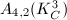 is a
is a 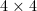 skew-symmetric matrix of linear forms in
skew-symmetric matrix of linear forms in 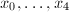 which has rank 2 on
which has rank 2 on 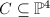 , hence its Pfaffian is a linear combination of the four quartics. The ring of semi-invariants of
, hence its Pfaffian is a linear combination of the four quartics. The ring of semi-invariants of 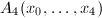 has 15 generators and
has 15 generators and 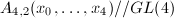 is the linear span of the four quartics
is the linear span of the four quartics 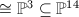 . Moreover, the stable moduli
. Moreover, the stable moduli 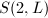 is the complement
is the complement 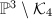 , where
, where 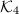 is known as the Kummer quartic surface.
is known as the Kummer quartic surface.
References
[1]An introduction to invariants and moduli, Cambridge University Press, 2003.
[2]Vector Bundles on Algebraic Curves, 2002, http://www.mimuw.edu.pl/~jarekw/EAGER/Lukecin02.html.
[3]Projective invariants of projective structures and applications, Proc. Internal. Congr. Math., 1962, 526--530.
[4]Space of Unitary Vector Bundles on a Compact Riemann Surface, The Annals of Mathematics 85 (1967), no.2, pp. 303-336.
[5]The geometry of moduli spaces of sheaves, University Press, 2010.
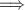 simple
simple 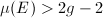 , then
, then 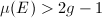 , then
, then 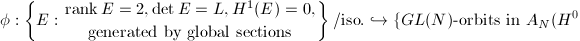
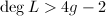 ,
, 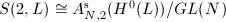 is a smooth quasi-projective variety.
is a smooth quasi-projective variety.
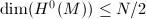 (
(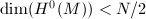 ).
).