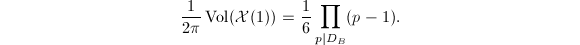In the 60s, Shimura studied certain algebraic curves as analogues of classical modular curves in order to construct class fields of totally real number fields. These curves were later coined "Shimura curves" and vastly generalized by Deligne. We will take a tour of the rich geometry and arithmetic of Shimura curves. Along the way, we may encounter tessellations of disks, quaternion algebras, abelian surfaces, elliptic curves with CM, Hurwitz curves ... and the answer to life, the universe and everything.
This is a note I prepared for my first Trivial Notions talk at Harvard, Fall 2011. Our main sources are [1], [2], [3], [4] and [5].
Briefly speaking, Shimura curves are simply one-dimensional Shimura varieties. I have accomplished my trivial notion task because I have told you a trivial notion. But obviously it does not help much if you do not know what the term Shimura varieties means. It only takes 5 chapters in Milne's notes in order to define them — not too bad — but initially Shimura invented them really because they are natural analogues of classical modular curves.
 Review of Modular Curves
Review of Modular Curves
Let  be the upper half plane. Then
be the upper half plane. Then 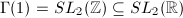 acts on
acts on  by Mobius transformations. For each complex number
by Mobius transformations. For each complex number 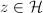 , we can associate an elliptic curve
, we can associate an elliptic curve 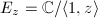 . The endomorphism ring is given by
. The endomorphism ring is given by 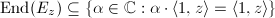 , which is either
, which is either 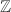 or an order in some imaginary quadratic field
or an order in some imaginary quadratic field 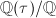 . The latter case is rarer and is given the name complex multiplication (CM). Two such elliptic curves
. The latter case is rarer and is given the name complex multiplication (CM). Two such elliptic curves 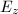 and
and 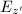 are isomorphic if and only if
are isomorphic if and only if 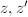 lie in the same
lie in the same 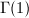 -orbit. Hence we have the following bijection.
-orbit. Hence we have the following bijection.
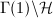 can be identified with the fundamental set
can be identified with the fundamental set 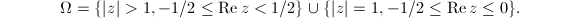 The elliptic point
The elliptic point 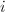 and
and 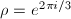 have nontrivial stabilizer of order 2 and 3, which correspond to elliptic curves with complex multiplication by
have nontrivial stabilizer of order 2 and 3, which correspond to elliptic curves with complex multiplication by ![$\mathbb{Z}[i]$](./latex/latex2png-ShimuraCurves_42772926_-5.gif) and
and ![$\mathbb{Z}[\rho]$](./latex/latex2png-ShimuraCurves_49444867_-5.gif) and automorphisms groups of order
and automorphisms groups of order 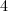 and
and 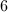 .
. 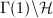 can be viewed as the Riemann sphere with the north pole missing. By adding the cusp
can be viewed as the Riemann sphere with the north pole missing. By adding the cusp 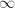 , we get the compactification
, we get the compactification 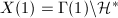 . The cusp has the moduli interpretation as degenerate elliptic curves — nodal cubic curves.
. The cusp has the moduli interpretation as degenerate elliptic curves — nodal cubic curves.
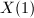 is the coarse moduli space of complex elliptic curves and is isomorphic to
is the coarse moduli space of complex elliptic curves and is isomorphic to 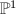 via the
via the 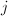 -invariant.
-invariant.
Analogously, for the congruence subgroups 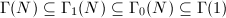 , where
, where
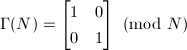 ,
,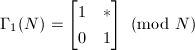 ,
, ,
,
we get the compact Riemann surfaces 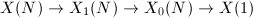 after adding cusps to the quotient
after adding cusps to the quotient 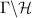 . These classical modular curves, which date back to Klein and Fricke in the 19th century, also play an important role in the modern proof of Fermat's last theorem. They are coverings of
. These classical modular curves, which date back to Klein and Fricke in the 19th century, also play an important role in the modern proof of Fermat's last theorem. They are coverings of 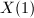 and are coarse moduli spaces of elliptic curves with additional torsion data:
and are coarse moduli spaces of elliptic curves with additional torsion data:
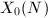 parametrizes elliptic curves with a
parametrizes elliptic curves with a 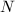 -cyclic subgroup.
-cyclic subgroup.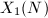 parametrizes elliptic curves with a point of order
parametrizes elliptic curves with a point of order 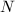 .
.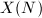 parametrizes elliptic curves with a basis of the
parametrizes elliptic curves with a basis of the 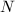 -torsion points with a fixed Weil pairing.
-torsion points with a fixed Weil pairing.
Due to the moduli interpretation, 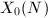 and
and 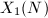 both have models over
both have models over  .
. 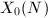 has the function field
has the function field 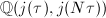 , so there is a polynomial
, so there is a polynomial ![$\Phi_n(x,y)\in \mathbb{Q}[x,y]$](./latex/latex2png-ShimuraCurves_216029304_-5.gif) such that
such that 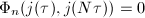 . A remarkable fact is that
. A remarkable fact is that 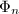 actually has integer coefficients. One can utilize this to show that for an elliptic curve
actually has integer coefficients. One can utilize this to show that for an elliptic curve 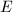 with CM by
with CM by 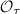 , where
, where 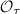 is the ring of integers of
is the ring of integers of 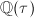 ,
, 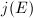 is actually an algebraic integer (Gross-Zagier have very explicit formula for these values). Moreover, the theory of complex multiplication shows:
is actually an algebraic integer (Gross-Zagier have very explicit formula for these values). Moreover, the theory of complex multiplication shows:
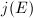 is an algebraic integer of degree
is an algebraic integer of degree 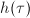 , where
, where 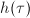 is the class number of the imaginary quadratic field
is the class number of the imaginary quadratic field 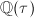 . The Hilbert class filed
. The Hilbert class filed 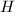 of
of 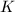 can be obtained from
can be obtained from 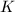 by adjoining
by adjoining 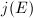 . The maximal abelian extension of
. The maximal abelian extension of 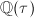 can be obtained by adjoining
can be obtained by adjoining 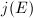 and the
and the  -coordinates of torsion points of
-coordinates of torsion points of 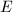 . Moreover, the action of
. Moreover, the action of 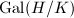 on
on 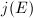 can be described explicitly.
can be described explicitly.
This main theorem of complex multiplication implies an interesting result discovered by Ramanujan: 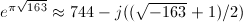 is an "almost integer" as
is an "almost integer" as 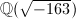 has class number 1!
has class number 1!
 Shimura curves
Shimura curves
One problem with 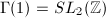 is that its fundamental domain
is that its fundamental domain 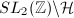 is not compact. As a consequence, every subgroup of
is not compact. As a consequence, every subgroup of 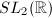 commensurable with
commensurable with 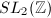 is not cocompact and we have to add cusps to obtain modular curves.
is not cocompact and we have to add cusps to obtain modular curves.
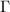 of
of 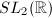 such that
such that 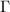 is cocompact?
is cocompact?
You have definitely seen many examples from the artwork of M. C. Escher. Using the Poincare disk model for 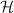 , we can tessellate
, we can tessellate 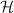 with infinitely many hyperbolic triangles with geodesic sides.
with infinitely many hyperbolic triangles with geodesic sides.
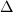 be the hyperbolic triangle with angles
be the hyperbolic triangle with angles 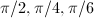 . Let
. Let 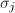 be the
be the 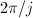 rotation with respect to its
rotation with respect to its 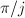 vertex (
vertex (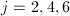 ). Then the group
). Then the group 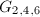 generated by
generated by 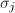 acts on
acts on  as automorphisms. Looking at the picture we obtain the representation
as automorphisms. Looking at the picture we obtain the representation 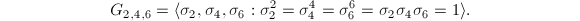 It is called the
It is called the  -triangle group and has the fundamental domain consisting of
-triangle group and has the fundamental domain consisting of 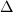 and one copy of its reflection. Hence
and one copy of its reflection. Hence 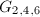 is a discrete cocompact subgroup of
is a discrete cocompact subgroup of 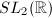 .
.

More generally, any triple 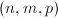 satisfying
satisfying 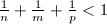 gives us a triangle group. It is a cocompact subgroup of
gives us a triangle group. It is a cocompact subgroup of 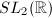 and has exactly three elliptic points of orders
and has exactly three elliptic points of orders 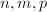 . From this point view,
. From this point view, 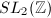 is simply the limiting case
is simply the limiting case 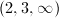 , where
, where 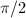 and
and 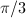 are the order 2 and 3 elliptic points and the cusp emerges as the limit
are the order 2 and 3 elliptic points and the cusp emerges as the limit 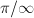 vertex.
vertex.
By "arithmetically" we mean the way we obtained 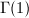 and other congruence subgroups by "taking
and other congruence subgroups by "taking 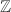 -points" of a matrix group. More precisely,
-points" of a matrix group. More precisely,
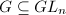 be an algebraic group over
be an algebraic group over 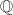 . A subgroup of
. A subgroup of 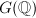 is called arithmetic if
is called arithmetic if 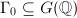 is commensurable with
is commensurable with 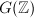 .
.
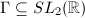 is called arithmetic if there exists an algebraic group
is called arithmetic if there exists an algebraic group 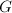 over
over 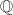 and a surjective homomorphism
and a surjective homomorphism 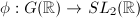 with compact kernel such that
with compact kernel such that 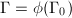 , where
, where 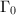 is an arithmetic subgroup of
is an arithmetic subgroup of 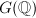 .
.
Roughly speaking, after ignoring compact factors, an arithmetic subgroup of 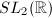 is simply a subgroup commensurable with
is simply a subgroup commensurable with 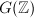 provided
provided 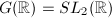 . The congruence subgroups of
. The congruence subgroups of 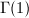 are obtained by taking
are obtained by taking 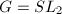 . But none of them are cocompact! In order get a cocompact arithmetic subgroup, we need to find some other algebraic group
. But none of them are cocompact! In order get a cocompact arithmetic subgroup, we need to find some other algebraic group 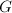 with
with 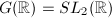 . Instead of working with the matrix algebra
. Instead of working with the matrix algebra 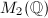 and
and 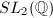 , we need some other
, we need some other 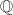 -algebra structure. One example is given by the quaternion algebra.
-algebra structure. One example is given by the quaternion algebra.
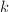 is a central simple
is a central simple 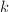 -algebra of dimension 4, namely a 4-dimensional
-algebra of dimension 4, namely a 4-dimensional 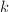 -algebra with center
-algebra with center 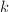 and no nontrivial two-sided ideals.
and no nontrivial two-sided ideals.
By Wedderburn's theorem, every central simple 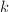 algebra is a matrix algebra over a central division
algebra is a matrix algebra over a central division 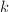 -algebra. All the central division
-algebra. All the central division 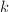 -algebra are classified by the Brauer group
-algebra are classified by the Brauer group 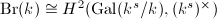 . Quaternion algebras are characterized from division
. Quaternion algebras are characterized from division 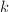 -algebras as those having a quadratic splitting field.
-algebras as those having a quadratic splitting field.
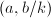 is the
is the 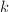 -algebra with basis
-algebra with basis 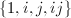 satisfying the relations
satisfying the relations 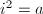 ,
, 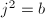 ,
, 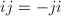 , where
, where 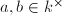 . Then
. Then 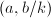 is a quaternion algebra. We can view
is a quaternion algebra. We can view 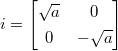 and
and 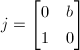 . Then
. Then 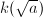 splits
splits 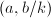 as
as 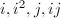 are
are 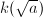 -linear independent. Conversely, every quaternion algebra (including
-linear independent. Conversely, every quaternion algebra (including 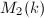 ) is of the form
) is of the form 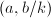 . One can regard quaternion algebras as a noncommutative way of gluing quadratic fields together. There is a natural involution given by
. One can regard quaternion algebras as a noncommutative way of gluing quadratic fields together. There is a natural involution given by 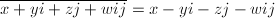 . The trace and norm are given by
. The trace and norm are given by 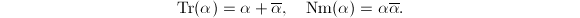
 , we have the matrix algebra
, we have the matrix algebra 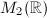 and the Hamilton quaternion
and the Hamilton quaternion 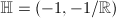 . As
. As 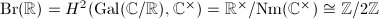 , these are the only two! Moreover, the norm one elements in
, these are the only two! Moreover, the norm one elements in 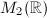 form
form 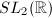 and the norm one elements in
and the norm one elements in 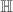 form a compact group.
form a compact group.
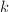 a non-archimedean local field, one big result from local class field theory tells us that
a non-archimedean local field, one big result from local class field theory tells us that 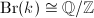 and quaternion algebras are classified by
and quaternion algebras are classified by ![$\mathrm{Br}(k)[2 ]\cong \mathbb{Z}/2 \mathbb{Z}$](./latex/latex2png-ShimuraCurves_157065750_-5.gif) . Again there is a unique nonsplit quaternion algebra.
. Again there is a unique nonsplit quaternion algebra.
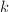 a number field, one big result from global class field theory tells us that
a number field, one big result from global class field theory tells us that 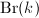 sits inside an exact sequence
sits inside an exact sequence 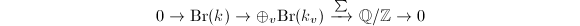 and quaternion algebras are classified by
and quaternion algebras are classified by ![$\mathrm{Br}(k)[2 ]$](./latex/latex2png-ShimuraCurves_170405697_-5.gif) . So there are many quaternion algebras
. So there are many quaternion algebras 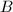 over
over 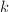 , each of which is uniquely determined by an even number of nonsplit places. The discriminant
, each of which is uniquely determined by an even number of nonsplit places. The discriminant 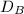 of
of 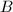 is product of all nonsplit places of
is product of all nonsplit places of 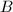 . So for
. So for 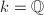 , any finite set
, any finite set 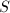 of finite primes will give a unique rational quaternion algebra, which is split at
of finite primes will give a unique rational quaternion algebra, which is split at 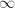 if
if 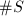 is even and nonsplit at
is even and nonsplit at 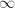 if
if 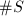 is odd. In particular, a quaternion algebras split at every place is just the usual matrix algebra
is odd. In particular, a quaternion algebras split at every place is just the usual matrix algebra 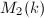 .
.
Now on let 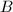 be a rational quaternion algebra split at
be a rational quaternion algebra split at 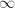 . We can generalize the procedure of taking
. We can generalize the procedure of taking 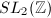 from
from 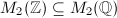 by taking a maximal order (a
by taking a maximal order (a 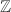 -lattice of rank 4 which also a subring)
-lattice of rank 4 which also a subring) 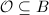 and its norm 1 elements
and its norm 1 elements 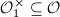 . Since
. Since 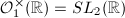 ,
, 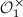 is an arithmetic subgroup of
is an arithmetic subgroup of 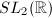 . As
. As 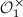 has no parabolic elements, we know that
has no parabolic elements, we know that 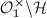 is cocompact. The resulting complex algebraic curve is the counterpart of the classical modular curve
is cocompact. The resulting complex algebraic curve is the counterpart of the classical modular curve 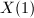 .
.
 Moduli interpretation and class fields
Moduli interpretation and class fields
Now given any 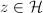 , we have a rank 4-lattice
, we have a rank 4-lattice 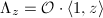 in
in 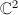 , where we view
, where we view 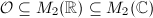 . So we obtain a complex torus
. So we obtain a complex torus 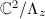 with an
with an 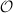 -action. It is actually an abelian surface via the Riemann form
-action. It is actually an abelian surface via the Riemann form 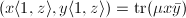 , where
, where 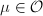 is chosen in the way that
is chosen in the way that 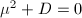 . A special case is when
. A special case is when 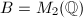 and
and 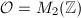 ,
, 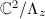 is just two copies of the elliptic curve
is just two copies of the elliptic curve 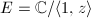 . So the same logic should apply and we can check that
. So the same logic should apply and we can check that
In this case we say 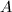 is a QM-surface (quaternionic multiplication). For a fixed choice of
is a QM-surface (quaternionic multiplication). For a fixed choice of 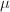 , a theorem of Milne implies that if there is an embedding
, a theorem of Milne implies that if there is an embedding 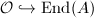 , then there is a unique principal polarization
, then there is a unique principal polarization 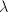 of
of 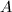 such that the corresponding Rosati involution
such that the corresponding Rosati involution 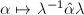 on
on 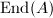 coincides with the positive involution
coincides with the positive involution 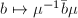 on
on 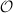 .
.
Now assume 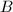 is nonsplit and let
is nonsplit and let 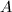 be a QM-surface.
be a QM-surface.
- If
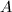 is simple, then its endomorphism algebra
is simple, then its endomorphism algebra 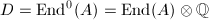 is an division algebra.
is an division algebra. 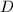 acts on
acts on 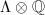 freely, so
freely, so 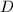 has dimension at most 4. But
has dimension at most 4. But 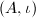 is QM, so
is QM, so 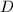 has dimension at least 4 and
has dimension at least 4 and 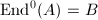 .
. - If
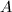 is not simple, then
is not simple, then 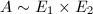 . If
. If 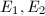 are not isogenous, then
are not isogenous, then 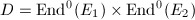 which cannot contain the quaternion algebra
which cannot contain the quaternion algebra 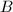 . Hence
. Hence 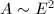 and
and 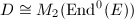 . Since
. Since 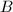 is nonsplit, we know that
is nonsplit, we know that 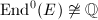 , hence
, hence 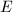 is an elliptic curve with CM by a field
is an elliptic curve with CM by a field 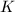 which splits
which splits 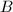 .
.
So we have proved the following
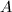 is a QM-surface. Then either
is a QM-surface. Then either 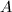 is simple with
is simple with 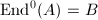 or
or 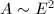 , where
, where 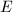 is an elliptic curve with CM by a field which splits
is an elliptic curve with CM by a field which splits 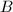 .
.
In the latter case, the corresponding point on the Shimura curve 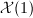 is called a CM point. Those are in some sense "degenerate" points on the moduli space of QM-surfaces. One can expect that these CM points could play an important role, since, unlike the modular curves case, we do not have truly degenerate cusps to work with.
is called a CM point. Those are in some sense "degenerate" points on the moduli space of QM-surfaces. One can expect that these CM points could play an important role, since, unlike the modular curves case, we do not have truly degenerate cusps to work with.
Due to the moduli interpretation, 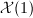 has a canonical model over
has a canonical model over 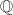 . More generally, one can define the order
. More generally, one can define the order 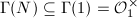 by imposing a congruence condition
by imposing a congruence condition 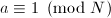 . The resulting Shimura curve
. The resulting Shimura curve 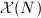 has a similar moduli interpretation as QM-surfaces with extra level-
has a similar moduli interpretation as QM-surfaces with extra level-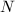 structures, which I do not quite bother writing down here.
structures, which I do not quite bother writing down here.
Instead of 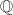 , one can also work more generally with a totally real number field
, one can also work more generally with a totally real number field 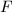 of degree
of degree ![$[F:\mathbb{Q}]=n$](./latex/latex2png-ShimuraCurves_12169831_-5.gif) and a quaternion algebra
and a quaternion algebra 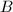 over
over 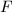 split only at one real place. Then we have an embedding from
split only at one real place. Then we have an embedding from 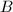 to the split factor
to the split factor 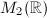 of
of 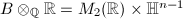 . Then norm one element
. Then norm one element 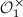 in the maximal order
in the maximal order 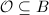 will again form a cocompact arithmetic subgroup of
will again form a cocompact arithmetic subgroup of 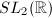 and the quotient
and the quotient 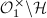 is a Shimura curve. These curves also have a moduli interpretation as abelian varieties of dimension
is a Shimura curve. These curves also have a moduli interpretation as abelian varieties of dimension 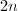 with
with 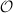 -actions, which is more complicated than the
-actions, which is more complicated than the 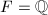 case. Using the moduli interpretation, Shimura proved that
case. Using the moduli interpretation, Shimura proved that 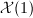 has a canonical model
has a canonical model 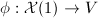 , where
, where 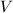 is a complete algebraic curve over
is a complete algebraic curve over 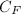 , the maximal abelian extension of
, the maximal abelian extension of 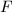 unramified at all finite primes. Shimura then constructed class fields for totally imaginary extension of totally real number fields:
unramified at all finite primes. Shimura then constructed class fields for totally imaginary extension of totally real number fields:
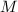 be a totally imaginary extension of
be a totally imaginary extension of 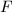 , which is isomorphic to a quadratic subfield of
, which is isomorphic to a quadratic subfield of 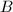 over
over 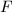 . Then the Hilbert class field
. Then the Hilbert class field 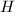 of
of 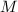 is obtained from
is obtained from 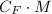 by adjoining
by adjoining 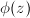 for
for  a regular fixed point of
a regular fixed point of 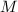 on
on 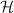 .
.
Whatever the word "regular fixed point" means, it can be viewed as an analogue of the value of 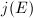 in the modular curves case. Moreover, the action of
in the modular curves case. Moreover, the action of 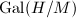 can be described explicitly by the Shimura reciprocity law. We shall not go into the excessive details here.
can be described explicitly by the Shimura reciprocity law. We shall not go into the excessive details here.
 Hurwitz curves
Hurwitz curves
Now let us look at an interesting example of Shimura curves which relates to
In the mathematical context, you may have seen this magic number as a bound for the number of automorphisms of a complex algebraic curve 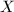 .
.
You know the proof if you went to Anand's class and listened carefully. Those curves with equality are called Hurwitz curves. Now let me show you how quaternion algebras and Shimura curves could help us in finding Hurwitz curves. Let us get started by finding a volume formula for the fundamental domain of 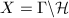 . Suppose
. Suppose 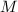 is the half fundamental domain consisting of
is the half fundamental domain consisting of 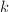 elliptic points of orders
elliptic points of orders 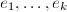 and
and 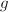 quadruples of sides which are glued together in a way you all know. By the Gauss-Bonnet formula
quadruples of sides which are glued together in a way you all know. By the Gauss-Bonnet formula 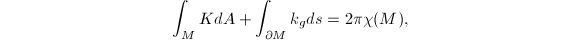 where
where 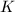 is the Gaussian curvature of
is the Gaussian curvature of 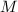 ,
, 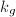 is the geodesic curvature of
is the geodesic curvature of 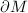 . In our case,
. In our case, 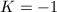 ,
, 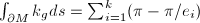 and
and 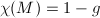 . Therefore,
. Therefore, 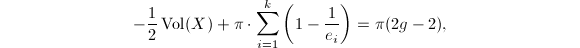 In other words, we recover the Riemann-Hurwitz formula,
In other words, we recover the Riemann-Hurwitz formula, 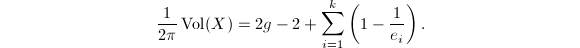 A simple calculation shows that the fundamental domain has the minimal volume
A simple calculation shows that the fundamental domain has the minimal volume 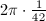 when
when 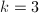 ,
, 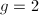 and
and 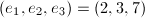 , which corresponds to
, which corresponds to 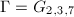 . Suppose
. Suppose 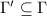 is a normal subgroup, then we know
is a normal subgroup, then we know 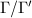 acts on
acts on 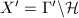 as automorphisms and
as automorphisms and ![$[\Gamma:\Gamma']=\Vol(X')/\Vol(X)$](./latex/latex2png-ShimuraCurves_184772378_-5.gif) . If
. If 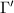 furthermore has no elliptic points, then
furthermore has no elliptic points, then 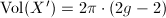 , hence
, hence 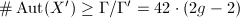 and
and 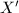 is indeed a Hurwitz curve!
is indeed a Hurwitz curve!
The remarkable thing is that 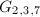 is actually an arithmetic subgroup coming from a quaternion algebra. How can one possibly figure this out? The above volume formula is true for an arbitrary discrete subgroup
is actually an arithmetic subgroup coming from a quaternion algebra. How can one possibly figure this out? The above volume formula is true for an arbitrary discrete subgroup 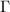 . But since arithmetic subgroups are defined in an arithmetic way, so one could expect that the arithmetic properties of quaternion algebras would benefit us. This is the case and here is an amazing volume formula worked out by Shimizu [6] using only arithmetic properties.
. But since arithmetic subgroups are defined in an arithmetic way, so one could expect that the arithmetic properties of quaternion algebras would benefit us. This is the case and here is an amazing volume formula worked out by Shimizu [6] using only arithmetic properties.
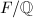 be a totally real number field of degree
be a totally real number field of degree 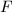 . Then
. Then 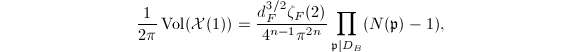 where
where 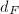 is the discriminant of
is the discriminant of 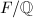 ,
, 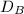 is the discriminant of
is the discriminant of 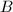 and
and 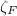 is the Dedekind zeta function of
is the Dedekind zeta function of 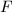 .
.
Given a quaternion algebra, we can work out the volume of 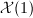 with Shimizu's formula in hand (and the zeta function is going to take over the world). Hence we can possibly solve
with Shimizu's formula in hand (and the zeta function is going to take over the world). Hence we can possibly solve 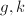 and
and 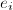 using the general volume formula. In fact,
using the general volume formula. In fact, 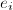 can also be determined by investigating arithmetics by the work of Eichler. So one can sit down and work hard with quaternion algebras with a hope of finding triangle groups, i.e. those with
can also be determined by investigating arithmetics by the work of Eichler. So one can sit down and work hard with quaternion algebras with a hope of finding triangle groups, i.e. those with 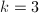 and
and 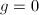 . The complete list of arithmetic triangle groups are determined by Takeuchi [7], [8].
. The complete list of arithmetic triangle groups are determined by Takeuchi [7], [8].
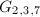 can be identified the group
can be identified the group 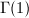 for the cubic totally real field
for the cubic totally real field 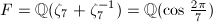 and the quaternion algebras
and the quaternion algebras 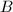 over
over 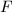 only nonsplit at two real places. As discussed above, any normal subgroup
only nonsplit at two real places. As discussed above, any normal subgroup 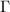 of
of 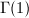 gives us a Hurwitz curve if it has no elliptic points. It turns out that the congruence subgroup
gives us a Hurwitz curve if it has no elliptic points. It turns out that the congruence subgroup 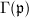 has no elliptic points for any ideal
has no elliptic points for any ideal 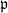 of
of 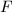 , hence gives sn infinite family of Hurwitz curves! Even better, the number of automorphisms can be computed as
, hence gives sn infinite family of Hurwitz curves! Even better, the number of automorphisms can be computed as 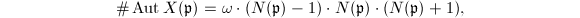 where
where 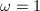 if
if 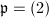 and
and 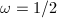 otherwise. The first few with small values of genus are listed as follows.
otherwise. The first few with small values of genus are listed as follows.
- For the ramified prime over 7,
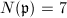 . So
. So 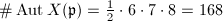 ,
, 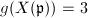 and
and 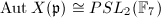 .. It is known as the Klein quartic with the model
.. It is known as the Klein quartic with the model 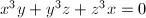 .
. - For the inert prime over 2,
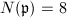 . So
. So 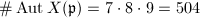 ,
, 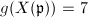 and
and 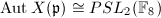 . It is known as the Fricke-Macbeath curve.
. It is known as the Fricke-Macbeath curve. - For the three unramified primes over 13,
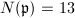 . So we have three curves with
. So we have three curves with 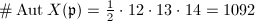 ,
, 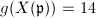 and
and 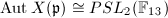 . These were unkown before Shimura and are called the first Hurwitz triplet.
. These were unkown before Shimura and are called the first Hurwitz triplet.
The above five are actually the first five smallest genus Hurwitz curves. The next one is of genus 17, which is non-arithmetic. The next arithmetic one is of genus 118 given by the inert prime above 3.
References
[1]Rational points on Atkin-Lehner quotients of Shimura curves, Harvard University Cambridge, Massachusetts, 2003.
[2]Construction of class fields and zeta functions of algebraic curves, The Annals of Mathematics 85 (1967), no.1, 58--159.
[3]Shimura curve computations, Arithmetic geometry 8 (2006), 103--113.
[4]Shimura curve computations, Algorithmic number theory (1998), 1--47.
[5]The Klein quartic in number theory, The Eightfold Way, edited by S. Lévy (1999), 51--102.
[6]On zeta functions of quaternion algebras, The Annals of Mathematics 81 (1965), no.1, 166--193.
[7]Commensurability classes of arithmetic triangle groups, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24 (1977), no.1, 201--212.
[8]Arithmetic triangle groups, J. Math. Soc. Japan 29 (1977), no.1, 91--106.
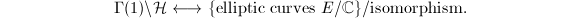
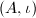 , where
, where 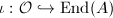 is an embedding.
is an embedding.
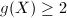 , then
, then 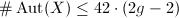 .
.