After recalling the category 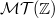 of mixed Tate motives over
of mixed Tate motives over 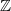 and its relationship with
and its relationship with 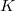 -groups, we discuss the basics of algebraic
-groups, we discuss the basics of algebraic 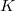 -theory and Borel's computation of the rational
-theory and Borel's computation of the rational 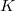 -groups of
-groups of 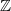 . We then explain how to use Borel's theorem to give a concrete description of the motivic Galois group of
. We then explain how to use Borel's theorem to give a concrete description of the motivic Galois group of 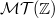 and bound the dimension of the span of multiple zeta values.
and bound the dimension of the span of multiple zeta values.
This is an expanded note prepared for a STAGE talk, Fall 2014. Our main references are [1],[2],[3], [4] and [5].
 Mixed Tate motives
Mixed Tate motives
Let 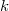 be a number field with ring of integers
be a number field with ring of integers 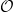 . Last time we introduced a neutral Tannakian category
. Last time we introduced a neutral Tannakian category 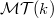 of mixed Tate motives over
of mixed Tate motives over 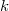 . Intuitively, it consists of mixed motives over
. Intuitively, it consists of mixed motives over 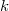 which are successive extensions of the Tate objects
which are successive extensions of the Tate objects 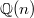 . Since the category of mixed motives
. Since the category of mixed motives 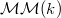 has yet to be constructed, we had to work around to define
has yet to be constructed, we had to work around to define 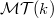 . People (e.g, Voevodsky) have constructed a triangulated tensor category
. People (e.g, Voevodsky) have constructed a triangulated tensor category 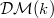 that behaves like the bounded derived category of the conjectural
that behaves like the bounded derived category of the conjectural 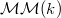 (even over more general base schemes). We take a triangulated tensor subcategory
(even over more general base schemes). We take a triangulated tensor subcategory 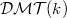 generated by the Tate objects. The Beilinson-Soule vanishing conjecture is true for
generated by the Tate objects. The Beilinson-Soule vanishing conjecture is true for 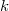 and it allows one to define a
and it allows one to define a  -structure on
-structure on 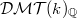 using its natural weight structure. The category of mixed Tate motives
using its natural weight structure. The category of mixed Tate motives 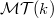 is then defined as the heart of this
is then defined as the heart of this 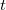 -structure (see [6]). We also introduced a subcategory
-structure (see [6]). We also introduced a subcategory 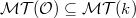 of mixed Tate motives over
of mixed Tate motives over 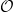 . The
. The  -adic realization of a mixed Tate motive defined over
-adic realization of a mixed Tate motive defined over 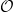 is unramified at any place
is unramified at any place 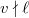 of
of 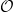 . These categories can be pictured as follows.
. These categories can be pictured as follows.
![$$\xymatrix@1@!C=1em{& \mathcal{DM}(k)& \supset &\mathcal{DMT}(k) \ar[d]^{\heartsuit} & &\\ & *+[F--]{\mathcal{MM}(k)} & \supset & \mathcal{MT}(k) & \supset & \mathcal{MT}(\mathcal{O}).}$$](./latex/latex2png-MixedTateMotives_8398203_.gif) Recall that the subcategory
Recall that the subcategory 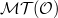 is defined via restricting the extension group
is defined via restricting the extension group 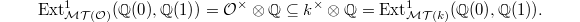 These can be reinterpreted as the first algebraic
These can be reinterpreted as the first algebraic  -group
-group  and the restriction can be viewed as a special case of the following theorem, which is a (highly nontrivial) consequence of the construction of
and the restriction can be viewed as a special case of the following theorem, which is a (highly nontrivial) consequence of the construction of 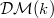 .
.
 Algebraic K-theory
Algebraic K-theory
We now briefly explain the basics of algebraic 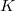 -theory (see [7] and [8]) and state Borel's theorem on these rational
-theory (see [7] and [8]) and state Borel's theorem on these rational 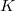 -groups of
-groups of 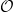 . Algebraic
. Algebraic 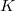 -theory is a sequence of functors
-theory is a sequence of functors 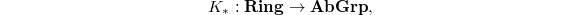 which, roughly speaking, extracts abelian invariants from "linear algebra construction" of
which, roughly speaking, extracts abelian invariants from "linear algebra construction" of  .
.
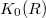 are abelian invariants of "vector spaces" over
are abelian invariants of "vector spaces" over 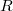 . The isomorphism classes of finitely generated projective modules over
. The isomorphism classes of finitely generated projective modules over 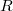 form a semigroup under the direct sum operation.
form a semigroup under the direct sum operation. 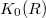 is defined to be the group completion (aka. Grothendieck group) of this semigroup. The analogy with topological
is defined to be the group completion (aka. Grothendieck group) of this semigroup. The analogy with topological 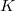 -theory is evident.
-theory is evident.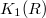 are abelian invariants of "matrices" over
are abelian invariants of "matrices" over 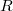 . Let
. Let 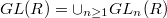 , where
, where 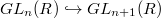 via
via 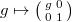 . Then
. Then 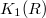 is defined to be
is defined to be ![$GL(R)^\mathrm{ab}=GL(R)/[GL(R),GL(R)]$](./latex/latex2png-MixedTateMotives_32190771_-5.gif) . In fact the commutator
. In fact the commutator ![$[GL(R),GL(R)]=E(R)$](./latex/latex2png-MixedTateMotives_214650769_-5.gif) , where
, where 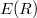 is generated by elementary matrices
is generated by elementary matrices 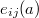 (1's on the diagonal,
(1's on the diagonal, 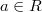 on the
on the 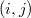 -entry).
-entry).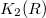 is defined to be the group homology
is defined to be the group homology 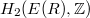 , which measures the relations between the elementary matrices
, which measures the relations between the elementary matrices 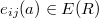 . Since
. Since 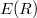 is perfect, i.e.,
is perfect, i.e., ![$[E(R),E(R)]=E(R)$](./latex/latex2png-MixedTateMotives_34424072_-5.gif) , we know that
, we know that 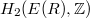 is isomorphic to the kernel of the universal central extension
is isomorphic to the kernel of the universal central extension 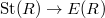 of
of 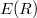 . Here
. Here 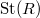 is known as the Steinberg group of
is known as the Steinberg group of 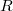 .
.
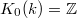 (= dimension of vector spaces over a field),
(= dimension of vector spaces over a field), 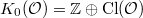 (each finitely generated projective
(each finitely generated projective 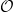 -module is isomorphic to a fractional ideal;
-module is isomorphic to a fractional ideal; 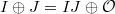 ).
).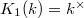 ,
, 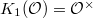 (a matrix
(a matrix  over a field or
over a field or  can be transformed via elementary matrices into
can be transformed via elementary matrices into 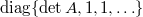 ; notice, however, this is not true for a general Dedekind domain
; notice, however, this is not true for a general Dedekind domain 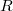 ).
).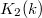 can be identified as Milnor's
can be identified as Milnor's 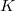 -group (defined for fields)
-group (defined for fields) 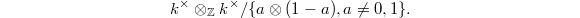
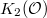 is known to a finite abelian group but harder to compute (it is known that
is known to a finite abelian group but harder to compute (it is known that 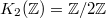 ).
).
 -groups may seem a bit random at first glance. The good thing is that they fit nicely in long exact sequence (like in usual cohomology theory):
-groups may seem a bit random at first glance. The good thing is that they fit nicely in long exact sequence (like in usual cohomology theory): 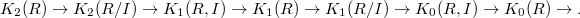 where
where 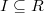 is an ideal and
is an ideal and 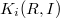 are suitably defined relative
are suitably defined relative 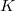 -groups. To further extend the long exact sequence to the left, Quillen came up with a uniform definition of all higher
-groups. To further extend the long exact sequence to the left, Quillen came up with a uniform definition of all higher 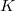 -groups rather than constructing them one by one in an ad hoc way. The idea is to realize
-groups rather than constructing them one by one in an ad hoc way. The idea is to realize 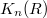 as the
as the 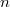 -th homotopy group
-th homotopy group 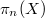 of a certain topological space
of a certain topological space 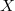 (or rather, its homotopy type), which is constructed from linear algebra over
(or rather, its homotopy type), which is constructed from linear algebra over 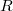 so that the
so that the 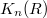 (
( ) matches up with the previous definitions. The above long exact then comes for free from the long exact homotopy sequence associated to a pair of spaces. Quillen gave two constructions:
) matches up with the previous definitions. The above long exact then comes for free from the long exact homotopy sequence associated to a pair of spaces. Quillen gave two constructions:
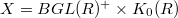 , where
, where 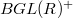 is the
is the 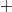 -construction applied to the classifying space
-construction applied to the classifying space 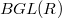 of
of 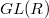 . The
. The 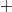 -construction of a topological space modifies its fundamental group but does not change its homology;
-construction of a topological space modifies its fundamental group but does not change its homology;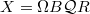 . Here
. Here 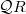 is a category whose objects are finitely generated projective
is a category whose objects are finitely generated projective 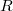 -modules and
-modules and  is the set of equivalence classes of diagrams
is the set of equivalence classes of diagrams 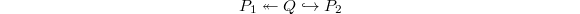 such that
such that 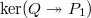 and
and 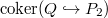 are also finitely generated
are also finitely generated  -modules.
-modules. 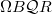 is the loop space of the classifying space of the category
is the loop space of the classifying space of the category 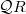 : so
: so 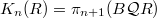 .
.
These two constructions look very different on the surface, but they turn out to produce the same 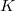 -groups.
-groups.
When 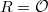 is the ring of integers of a number field
is the ring of integers of a number field 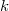 , Quillen proved that
, Quillen proved that 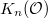 is always finitely generated. A celebrated theorem of Borel further computed the rank of
is always finitely generated. A celebrated theorem of Borel further computed the rank of 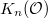 .
.
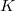 -groups are generally very difficult to compute. A useful consequence of Quillen's
-groups are generally very difficult to compute. A useful consequence of Quillen's 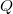 -construction is the localization theorem for computing
-construction is the localization theorem for computing 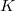 -groups. For example, for any Dedekind domain
-groups. For example, for any Dedekind domain 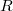 with fraction field
with fraction field 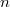 , there is a long exact sequence
, there is a long exact sequence 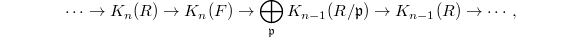 where
where 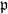 runs over all maximal ideals of
runs over all maximal ideals of 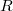 . For
. For 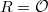 , more is true: Soule proved that the map
, more is true: Soule proved that the map 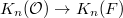 is injective, therefore by Example 2for each
is injective, therefore by Example 2for each 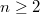 , we have
, we have 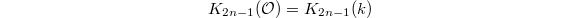 and for each
and for each 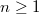 an exact sequence
an exact sequence 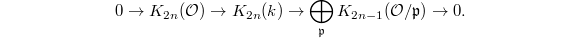 In particular, by Borel's theorem,
In particular, by Borel's theorem, 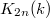 is an infinite torsion group.
is an infinite torsion group.
 . The Chern classes of algebraic
. The Chern classes of algebraic 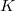 -theory
-theory 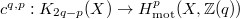 induce an isomorphism
induce an isomorphism ![$$K_{2q-p}(X)^{(q)}\cong H^p_\mathrm{mot}(X, \mathbb{Z}(q)) \otimes \mathbb{Q}:=\Hom_{\mathcal{DM}(k)}(\mathbb{Q}(0), \mathbb{Q}_X(q)[p]).$$](./latex/latex2png-MixedTateMotives_110278772_.gif) Here
Here 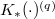 is the weight
is the weight 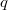 eigenspace of the Adams operators acting on
eigenspace of the Adams operators acting on 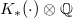 and
and 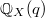 is an object in
is an object in 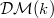 . Theorem 1 is a special case when
. Theorem 1 is a special case when 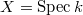 ,
, 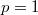 and
and 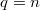 since
since 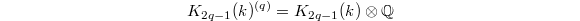 by a result of Soule. Also, for
by a result of Soule. Also, for 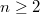 , the extension group
, the extension group 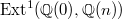 doesn't change when restricting to
doesn't change when restricting to  . Indeed we have
. Indeed we have 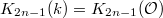 when
when 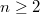 as in the previous remark.
as in the previous remark.
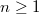 , the Dedekind zeta function
, the Dedekind zeta function 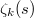 has order of vanishing equal to
has order of vanishing equal to 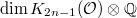 at
at 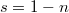 . More generally, Beilinson's first conjecture predicts the relation between order of vanishing of motivic
. More generally, Beilinson's first conjecture predicts the relation between order of vanishing of motivic 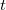 -function and motivic cohomology groups when
-function and motivic cohomology groups when 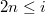 :
: 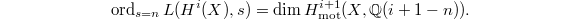 From this point of view, Borel's theorem verifies the special case
From this point of view, Borel's theorem verifies the special case 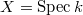 ,
, 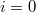 .
.
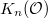 is harder to compute. People knew the case when
is harder to compute. People knew the case when 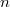 is odd. People also knew the order of
is odd. People also knew the order of 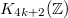 and conjectured that
and conjectured that 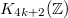 should be a cyclic group. The order
should be a cyclic group. The order 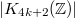 is related to the
is related to the 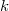 -th Bernoulli number: no surprise they should relate to the Riemann zeta function as well (Lichtenbaum's conjecture)! People also conjectured that
-th Bernoulli number: no surprise they should relate to the Riemann zeta function as well (Lichtenbaum's conjecture)! People also conjectured that 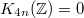 — this is in fact equivalent to Vandiver's conjecture on class groups of cyclotomic fields and seems to be extremely difficult.
— this is in fact equivalent to Vandiver's conjecture on class groups of cyclotomic fields and seems to be extremely difficult.
 Motivic Galois group of
Motivic Galois group of 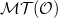
Recall that the de Rham realization functor 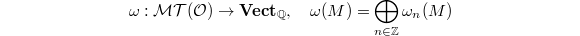 is a fiber functor (i.e., a faithful
is a fiber functor (i.e., a faithful  -linear exact tensor functor). Here
-linear exact tensor functor). Here 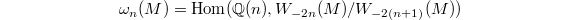 is multiplicity space of the weight
is multiplicity space of the weight 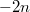 piece of
piece of 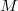 . This fiber functor
. This fiber functor  makes
makes 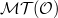 is neutral Tannakian category. We denote by
is neutral Tannakian category. We denote by 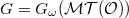 the corresponding Tannakian fundamental group. Then
the corresponding Tannakian fundamental group. Then 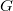 is a pro-algebraic group defined over
is a pro-algebraic group defined over 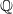 and
and 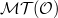 is equivalent to
is equivalent to 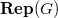 , the category of finite dimensional
, the category of finite dimensional 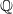 -representations of
-representations of 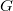 . Naturally
. Naturally 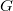 is called the motivic Galois group of
is called the motivic Galois group of 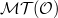 . By definition we have
. By definition we have 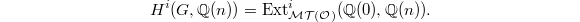 Our next goal is to give a concrete description of
Our next goal is to give a concrete description of 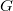 using this relation between the group cohomology of
using this relation between the group cohomology of 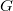 and the extension groups computed by Borel's theorem.
and the extension groups computed by Borel's theorem.
For any object 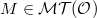 , we denote by
, we denote by 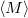 the full Tannakian subcategory generated by
the full Tannakian subcategory generated by 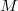 (whose objects are subquotients of
(whose objects are subquotients of 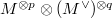 ). If
). If 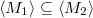 , then we have a surjection
, then we have a surjection 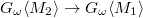 , which induces an isomorphism
, which induces an isomorphism 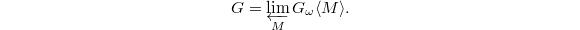 The "smallest" nontrivial Tannakian subcategory
The "smallest" nontrivial Tannakian subcategory 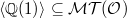 is nothing but the category of pure Tate motives over
is nothing but the category of pure Tate motives over 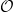 . Notice that
. Notice that 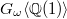 is determined by its action on the 1-dimensional vector space
is determined by its action on the 1-dimensional vector space 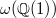 , hence is
, hence is 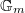 . This induces a surjection
. This induces a surjection 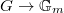 and we denote its kernel by
and we denote its kernel by 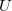 . Since
. Since 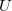 acts trivially on each graded piece of
acts trivially on each graded piece of 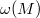 ,
, 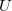 is pro-unipotent. Moreover, the exact sequence
is pro-unipotent. Moreover, the exact sequence 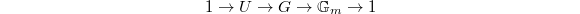 in fact splits: a splitting
in fact splits: a splitting 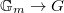 is given by
is given by  multiplication by
multiplication by  on
on 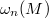 . This identifies
. This identifies 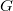 as the semi-direct product
as the semi-direct product 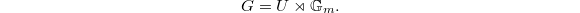 It remains to compute
It remains to compute 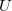 :
:
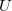 is a free pro-unipotent group generated by
is a free pro-unipotent group generated by 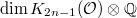 elements in degree
elements in degree 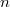 . In particular, when
. In particular, when 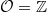 , it follows from Borel's theorem that
, it follows from Borel's theorem that 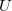 is a free pro-unipotent group with one generator in each odd degree
is a free pro-unipotent group with one generator in each odd degree 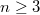 .
.
Let us review a bit background on pro-unipotent completions (see [9]). For any abstract group 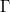 , its group algebra
, its group algebra ![$\mathbb{Q}[\Gamma]$](./latex/latex2png-MixedTateMotives_77372163_-5.gif) is naturally a Hopf algebra under
is naturally a Hopf algebra under 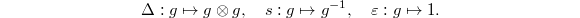 Moreover, the group
Moreover, the group 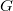 can be recovered as the group-like elements of the Hopf algebra
can be recovered as the group-like elements of the Hopf algebra ![$R=\mathbb{Q}[\Gamma]$](./latex/latex2png-MixedTateMotives_194812634_-5.gif) ,
, 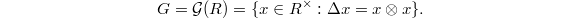 These two functors form an adjoint pair
These two functors form an adjoint pair ![$$\mathbb{Q}[\cdot]\{\text{Abstract groups}\}\rightleftarrows\{\text{Hopf algebras}\}: \mathcal{G}.$$](./latex/latex2png-MixedTateMotives_144563925_.gif) Notice that the Hopf algebra
Notice that the Hopf algebra ![$\mathbb{Q}[\Gamma]$](./latex/latex2png-MixedTateMotives_77372163_-5.gif) is cocommutative not necessarily commutative (it is commutative if and only if
is cocommutative not necessarily commutative (it is commutative if and only if 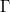 is abelian), hence does not correspond to the coordinate ring of an algebraic group. To obtain a commutative Hopf algebra, the natural idea is to take dual. To ensure taking dual is a reasonable operation, the topology on such Hopf algebras should not be too far away from finite dimensional vector spaces.
is abelian), hence does not correspond to the coordinate ring of an algebraic group. To obtain a commutative Hopf algebra, the natural idea is to take dual. To ensure taking dual is a reasonable operation, the topology on such Hopf algebras should not be too far away from finite dimensional vector spaces.
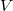 is linearly compact if it is homeomorphic to
is linearly compact if it is homeomorphic to 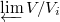 , where
, where 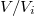 are discrete and finite dimensional. If
are discrete and finite dimensional. If 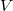 is linearly compact and
is linearly compact and 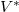 is its topological dual, then the linear dual
is its topological dual, then the linear dual 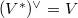 .
.
For a Hopf algebra 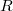 with argumentation ideal
with argumentation ideal 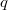 , the
, the 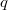 -adic completion
-adic completion 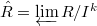 is is linearly compact if and only if
is is linearly compact if and only if 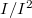 is finite dimensional. Restricting to such a subcategory we obtain a functor
is finite dimensional. Restricting to such a subcategory we obtain a functor 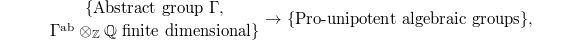 given by
given by ![$\Gamma\mapsto \Spec \widehat{\mathbb{Q}[\Gamma]}^*$](./latex/latex2png-MixedTateMotives_81247985_-5.gif) . Moreover, for a unipotent algebraic group
. Moreover, for a unipotent algebraic group  ,
, 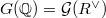 gives an adjoint functor (but not an equivalence).
gives an adjoint functor (but not an equivalence).
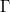 is a free abstract group on two generators
is a free abstract group on two generators 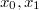 .
.
![$\mathbb{Q}[\Gamma]=\mathbb{Q}\langle x_0,x_1\rangle$](./latex/latex2png-MixedTateMotives_56909045_-5.gif) is the non-commutative polynomial ring in
is the non-commutative polynomial ring in 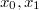 .
.![$\widehat{\mathbb{Q}[\Gamma]}=\mathbb{Q}\langle\langle y_0,y_1\rangle\rangle$](./latex/latex2png-MixedTateMotives_232390363_-5.gif) is the non-commutative power series ring in
is the non-commutative power series ring in 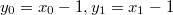 .
As a graded vector space,
.
As a graded vector space, ![$\widehat{\mathbb{Q}[\Gamma]}$](./latex/latex2png-MixedTateMotives_105474346_-5.gif) is isomorphic to the
is isomorphic to the 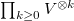 , where
, where 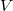 is a 2-dimensional vector space with basis
is a 2-dimensional vector space with basis 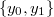 .
.![$G=\Spec \widehat{\mathbb{Q}[\Gamma]}^*$](./latex/latex2png-MixedTateMotives_235926146_-5.gif) is the free pro-unipotent group in two generators. As a graded vector space,
is the free pro-unipotent group in two generators. As a graded vector space, ![$\Spec \widehat{\mathbb{Q}[\Gamma]}^*=\bigoplus_{k\ge0}(V^\vee)^{\otimes k}$](./latex/latex2png-MixedTateMotives_93157956_-7.gif) . The algebra structure is given by the shuffle product and the coalgebra structure is given by de-concatenation.
. The algebra structure is given by the shuffle product and the coalgebra structure is given by de-concatenation.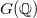 consists of group-like power series in
consists of group-like power series in ![$(\widehat{\mathbb{Q}[\Gamma]}^*)^\vee=\widehat{\mathbb{Q}[\Gamma]}=\mathbb{Q}\langle\langle y_0,y_1\rangle\rangle$](./latex/latex2png-MixedTateMotives_199045906_-5.gif) .
.
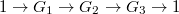 is an exact sequence of pro-unipotent groups, for a free pro-unipotent group
is an exact sequence of pro-unipotent groups, for a free pro-unipotent group 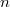 , any homomorphism
, any homomorphism 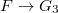 lifts to a homomorphism
lifts to a homomorphism 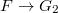 . Also analogous to usual group cohomology, for a pro-unipotent group
. Also analogous to usual group cohomology, for a pro-unipotent group 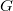 ,
, 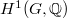 (resp.,
(resp., 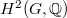 ) has an interpretation of generators (resp., relations). In particular, if
) has an interpretation of generators (resp., relations). In particular, if 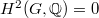 , then
, then 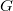 is a free pro-unipotent group, with generators given by a basis of
is a free pro-unipotent group, with generators given by a basis of 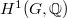 (see [10]).
(see [10]).
Now let us come back to our original situation 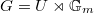 , where
, where 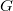 is the motivic Galois group of
is the motivic Galois group of 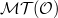 . The cohomology
. The cohomology 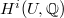 can be computed as follows. Theorem 3 then follows from it in view of the previous Remark 6 and Theorem 1.
can be computed as follows. Theorem 3 then follows from it in view of the previous Remark 6 and Theorem 1.
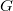 -representation
-representation 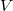 , the Hochschild-Serre spectral sequence implies that
, the Hochschild-Serre spectral sequence implies that 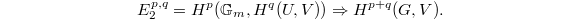 Since
Since 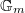 is reductive, we have
is reductive, we have 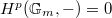 for
for 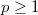 . Therefore,
. Therefore, 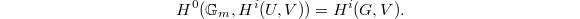 Now take
Now take 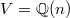 , we obtain that
, we obtain that 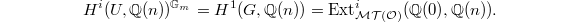 Since
Since 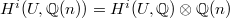 , we obtain that
, we obtain that 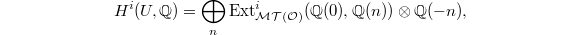 as desired.
¡õ
as desired.
¡õ
 Multiple zeta values
Multiple zeta values
Finally, we will use the concrete description of 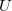 in Theorem 3 to give an explicit upper bound for the span of multiple zeta values. Recall that for
in Theorem 3 to give an explicit upper bound for the span of multiple zeta values. Recall that for 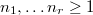 such that
such that 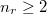 , the multiple zeta values is defined to be
, the multiple zeta values is defined to be 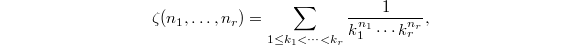 where
where  is called its depth and
is called its depth and 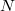 is called its weight. The depth
is called its weight. The depth 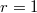 case recovers the classical zeta values
case recovers the classical zeta values 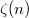 ,
, 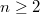 . These are transcendental real numbers satisfying a lot of mysterious relations (see [11]). We are interested in finding the dimension of the
. These are transcendental real numbers satisfying a lot of mysterious relations (see [11]). We are interested in finding the dimension of the  -linear span
-linear span 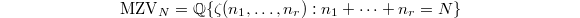 of multiple zeta values of weight
of multiple zeta values of weight 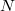 .
.
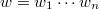 be a word in 0 and 1 starting with 1 and ending with 0. Let
be a word in 0 and 1 starting with 1 and ending with 0. Let 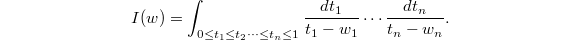 Then it is easy to see that
Then it is easy to see that 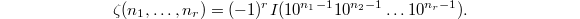 From this integral formula one can deduce that the product of two multiple zeta values with words
From this integral formula one can deduce that the product of two multiple zeta values with words 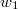 and
and 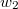 can be written as an
can be written as an 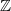 -linear combinations of other multiple zeta values (by shuffling
-linear combinations of other multiple zeta values (by shuffling 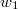 and
and 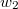 ). For example,
). For example, 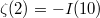 ,
, 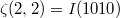 ,
, 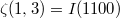 . The shuffle product of
. The shuffle product of 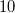 with
with 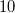 is
is 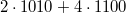 which implies the relation
which implies the relation 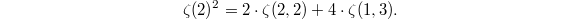 These are known as shuffle relations.
These are known as shuffle relations.
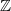 -linear combination by reordering the summation. For example,
-linear combination by reordering the summation. For example, 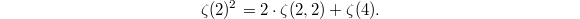 These relations are known as stuffle relations.
These relations are known as stuffle relations.
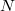 and depth
and depth  are the same when varying the depth
are the same when varying the depth  . For example,
. For example, 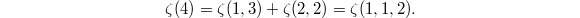
The following remarkable conjecture of Zagier predicts that though there are 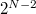 multiple zeta values with weight
multiple zeta values with weight 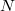 , the
, the 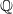 -span of them is much smaller.
-span of them is much smaller.
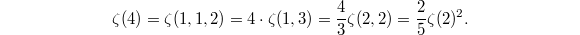 In particular,
In particular, 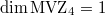 as predicted (these are all rational multiples of
as predicted (these are all rational multiples of 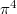 !) Zagier's conjecture can be checked for small values of
!) Zagier's conjecture can be checked for small values of 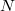 (this is done at least for
(this is done at least for 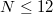 ), which probably serves as a good reason for making such a conjecture.
), which probably serves as a good reason for making such a conjecture.
Using the concrete description of pro-unipotent group 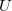 , we are now able to prove the following upper bound.
, we are now able to prove the following upper bound.
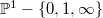 , and then define a graded algebra
, and then define a graded algebra 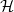 consisting of motivic multiple zeta values
consisting of motivic multiple zeta values 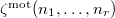 whose image under a period map are the classical multiple zeta values
whose image under a period map are the classical multiple zeta values 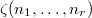 .
.
More precisely, let 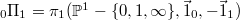 be the motivic torsor of paths from 0 to 1. Evaluating a regular function on
be the motivic torsor of paths from 0 to 1. Evaluating a regular function on 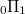 at the straight path
at the straight path 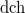 (droit chemin in French) from 0 to 1 gives a homomorphism
(droit chemin in French) from 0 to 1 gives a homomorphism 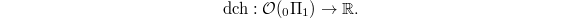 Concretely,
Concretely, 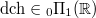 is a group-like power series in two letters 0 and 1 (see Example 3) whose coefficient before a word
is a group-like power series in two letters 0 and 1 (see Example 3) whose coefficient before a word  is given by the iterated integral
is given by the iterated integral 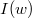 . Recall that
. Recall that 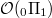 is an ind-object in
is an ind-object in 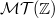 and thus
and thus 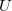 acts on it. Then
acts on it. Then 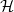 is defined to be the quotient of
is defined to be the quotient of 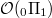 by the "motivic relations" between multiple zeta values: namely the quotient
by the "motivic relations" between multiple zeta values: namely the quotient 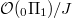 by the largest ideal
by the largest ideal 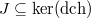 which is stable under the action of
which is stable under the action of 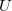 .
.
By Theorem 3, we have 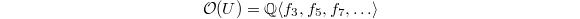 as a graded vector space (where
as a graded vector space (where 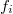 has degree
has degree 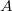 ). It turns out that one can find a (non-canonical) injective
). It turns out that one can find a (non-canonical) injective  -comodule morphism
-comodule morphism ![$$ \mathcal{H}\hookrightarrow \mathcal{H}^{\mathcal{MT}_+}:=\mathcal{O}(U) \otimes_\mathbb{Q} \mathbb{Q}[f_2]$$](./latex/latex2png-MixedTateMotives_77871642_.gif) which maps
which maps 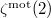 to
to 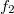 and
and 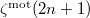 to
to 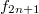 . Clearly an upper bound on the dimension of the weight
. Clearly an upper bound on the dimension of the weight 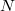 piece
piece 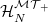 of
of 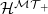 gives an upper bound on
gives an upper bound on 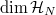 , hence on
, hence on 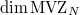 .
.
Now the point is that we can compute 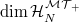 explicitly! It is the coefficients of
explicitly! It is the coefficients of 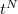 in the generating series
in the generating series 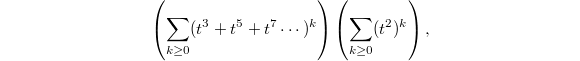 which is equal to
which is equal to 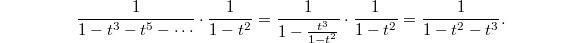 This last generating series is nothing but
This last generating series is nothing but  !
¡õ
!
¡õ
References
[1]Mixed Tate motives over $\Bbb Z$, Ann. of Math. (2) 175 (2012), no.2, 949--976.
[2]Motivic periods and the projective line minus three points, ArXiv e-prints (2014).
[3]On multiple zeta values, www.ihes.fr/~brown/Arbeitstatung.pdf.
[4]Groupes fondamentaux motiviques de Tate mixte, Ann. Sci. &EACUTE;cole Norm. Sup. (4) 38 (2005), no.1, 1--56.
[5]Tannakian fundamental groups associated to Galois groups, Galois groups and fundamental groups, Math. Sci. Res. Inst. Publ., 41 Cambridge Univ. Press, Cambridge, 2003, 183--216.
[6]Tate motives and the vanishing conjectures for algebraic $K$-theory, Algebraic $K$-theory and algebraic topology (Lake Louise, AB, 1991), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 407 Kluwer Acad. Publ., Dordrecht, 1993, 167--188.
[7]Algebraic $K$-theory and its applications, Springer-Verlag, New York, 1994.
[8]Algebraic $K$-theory of rings of integers in local and global fields, Handbook of $K$-theory. Vol. 1, 2, Springer, Berlin, 2005, 139--190.
[9]The pro-unipotent completion, http://perso.univ-rennes1.fr/alberto.vezzani/Files/Research/prounipotent.pdf.
[10]Cohomology of unipotent and prounipotent groups, J. Algebra 74 (1982), no.1, 76--95.
[11]Relations among multiple zeta values, http://www2.mathematik.hu-berlin.de/~mzv/mzv2013.pdf.
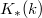 be the algebraic
be the algebraic 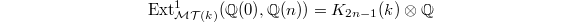 and
and 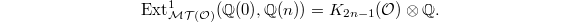 Moreover, all higher
Moreover, all higher 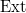 -groups vanish.
-groups vanish.
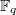 , Quillen computed that
, Quillen computed that 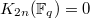 and
and 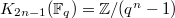 for
for 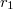 and
and 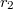 is the number of real and complex places of
is the number of real and complex places of 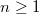 ,
, 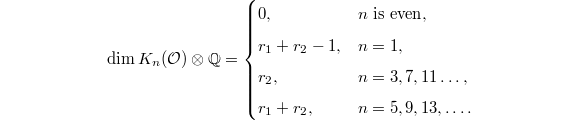
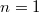 , Borel's theorem recovers Dirichlet's unit theorem.
, Borel's theorem recovers Dirichlet's unit theorem.
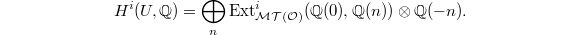
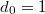 ,
, 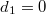 ,
, 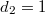 and
and 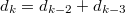 for
for 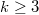 . Then
. Then 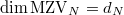 .
.
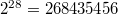 multiple zeta values of weight
multiple zeta values of weight 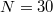 , but
, but 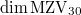 is conjecturally only
is conjecturally only 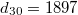 .
.
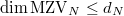 .
.