We start with an overview of heights on projective spaces and varieties to give a hint about their role in attacking finiteness problems of abelian varieties. We then try to explain the motivation for introducing the Faltings height on abelian varieties and do explicit computation in the case of elliptic curves. Finally we include a direct proof of the finiteness theorems of elliptic curves. Our main sources are [1], [2] and [3]. See also [4] and [5]. This is a note prepared for the Faltings' Theorem seminar at Harvard.
 Heights on projective spaces and projective varieties
Heights on projective spaces and projective varieties
Let us start by reviewing several basic properties of heights on projective spaces. The general scheme of height functions is a measurement of "arithmetic complexity". For a rational number 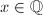 , we can write it as
, we can write it as 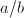 for two integers
for two integers 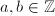 without common divisors, and define the height of
without common divisors, and define the height of  as
as 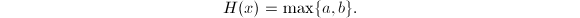 It will be troublesome to draw a graph of this "function" defined on
It will be troublesome to draw a graph of this "function" defined on 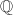 . Nevertheless, the definition matches our intuition: the larger
. Nevertheless, the definition matches our intuition: the larger 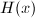 is, the more complicated
is, the more complicated  is.
is.
More intrinsically, let 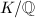 be a number field. Set the absolute values:
be a number field. Set the absolute values:
 satisfies
satisfies 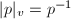 for
for 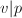 and
and 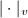 is the real or complex absolute value for
is the real or complex absolute value for  real or complex.
real or complex.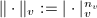 , where
, where ![$n_v=[K_v:\mathbb{Q}_v]$](./latex/latex2png-HeightsAndFiniteness_88391261_-5.gif) . It takes the value
. It takes the value 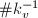 on the uniformizer
on the uniformizer 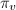 .
.
Note that by the product formula, 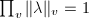 for
for 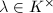 , thus we know that
, thus we know that 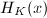 does not depend on the choice of homogeneous coordinates
does not depend on the choice of homogeneous coordinates ![$[a,b]$](./latex/latex2png-HeightsAndFiniteness_35152_-5.gif) . Because for
. Because for 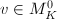 ,
, 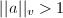 if and only if
if and only if 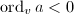 , it is easy to check that
, it is easy to check that
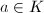 generates the ideal
generates the ideal 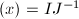 , where
, where 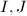 are relative prime integral ideals of
are relative prime integral ideals of  , then
, then 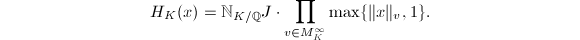
This definition of heights extends to projective spaces 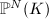 of dimension
of dimension  in an obvious way.
in an obvious way.
![$x=[x_0,\ldots x_N]\in \mathbb{P}^N(K)$](./latex/latex2png-HeightsAndFiniteness_41753293_-5.gif) . We define the relative height
. We define the relative height 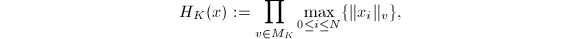 the absolute height
the absolute height ![$$H(x):=H_K(x)^{1/[K:\mathbb{Q}]},$$](./latex/latex2png-HeightsAndFiniteness_247659961_.gif) and the logarithmic height
and the logarithmic height 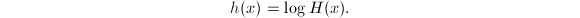 Note that for a finite extension
Note that for a finite extension 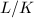 ,
, ![$H_L(x)=H_K(x)^{[L:K]}$](./latex/latex2png-HeightsAndFiniteness_220823940_-5.gif) , therefore the absolute height and the logarithmic height do not depend on the choice of
, therefore the absolute height and the logarithmic height do not depend on the choice of  .
.
The following is a prototype of a finiteness result under the bounded height condition.
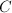 and
and 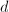 , there are only finitely many points
, there are only finitely many points 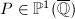 satisfying
satisfying 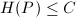 and
and ![$[\mathbb{Q}(P):\mathbb{Q}]\le d$](./latex/latex2png-HeightsAndFiniteness_263749229_-5.gif) . In particular, for any number field
. In particular, for any number field  , there are only finitely many points
, there are only finitely many points 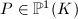 with bounded height.
with bounded height.
![$P=[x,1]$](./latex/latex2png-HeightsAndFiniteness_259131458_-5.gif) and let
and let 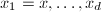 be the Galois conjugates of
be the Galois conjugates of  . Then the minimal polynomial of
. Then the minimal polynomial of  is of the form
is of the form 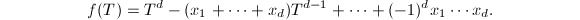 Note that the heights of the
Note that the heights of the 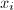 's are all the same, therefore the coefficient of
's are all the same, therefore the coefficient of 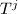 is bounded by
is bounded by 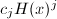 for some constant
for some constant 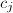 not depending on
not depending on  . So these coefficients are rational numbers with bounded heights, therefore there are only finitely many choices of the coefficients, hence finitely many choices of
. So these coefficients are rational numbers with bounded heights, therefore there are only finitely many choices of the coefficients, hence finitely many choices of 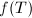 .
¡õ
.
¡õ
Here comes a neat corollary of the Northcott's property.
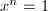 for some
for some 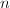 . Then
. Then 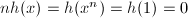 , hence
, hence 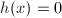 . Conversely, suppose
. Conversely, suppose 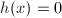 , then
, then 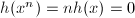 for every
for every 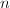 . By the Northcott's, some
. By the Northcott's, some 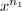 and
and 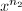 have to be same, which implies
have to be same, which implies  is a root of unity.
¡õ
is a root of unity.
¡õ
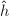 , called the canonical height (or Neron-Tate height) attached to every rational point on an abelian variety over
, called the canonical height (or Neron-Tate height) attached to every rational point on an abelian variety over  . It measures the arithmetic complexity of the point: for example,
. It measures the arithmetic complexity of the point: for example, 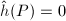 if and only if
if and only if  is a torsion point analogously.
is a torsion point analogously.
Slightly more generally, given a projective variety 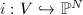 , the embedding
, the embedding 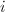 associates with every point
associates with every point 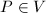 a height
a height 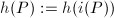 using the height on the projective space
using the height on the projective space 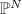 . The height thus obtained does depend on the choice of the projective embedding, nevertheless, it turns out to be uniquely determined up to a bounded function. From the previous theorem, we know that over a number field
. The height thus obtained does depend on the choice of the projective embedding, nevertheless, it turns out to be uniquely determined up to a bounded function. From the previous theorem, we know that over a number field  , there are only finitely many points in
, there are only finitely many points in 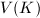 with bounded heights.
with bounded heights.
 Finiteness of abelian varieties and Modular Heights
Finiteness of abelian varieties and Modular Heights
One of the key steps in proving Faltings' theorem is to prove the finiteness theorems of abelian varieties.
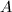 be an abelian variety over a number field
be an abelian variety over a number field  . Then there are only finitely many isomorphism classes of abelian varieties over
. Then there are only finitely many isomorphism classes of abelian varieties over  isogenous to
isogenous to 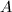 .
.
 of dimension
of dimension 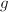 having good reduction outside a finite set of places
having good reduction outside a finite set of places 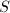 .
.
Carl has showed the implication
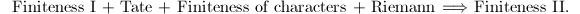 So it remains to show Finiteness I. Faltings' argument involves the usage of "heights":
So it remains to show Finiteness I. Faltings' argument involves the usage of "heights":
Height I There are only finitely many isomorphism classes of polarized abelian varieties 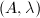 over
over  of dimension
of dimension 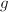 ,
, 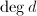 with semistable reduction everywhere and bounded "heights".
with semistable reduction everywhere and bounded "heights".
Height II The "height" is bounded in every isogeny class of abelian varieties over  .
.
Assuming these two parts, then together with the semistable reduction theorem (every abelian variety has semistable reduction after a finite extension), we can easily deduce Finiteness I.
To possibly show the finiteness statement like Height I, we would like to associate a height to each abelian variety using Northcott's property. A natural option is to view an abelian variety as a point in the Siegel moduli variety and attach the height of that point to the corresponding abelian varieties. This motivates the notion of modular heights.
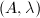 be a polarized abelian variety over
be a polarized abelian variety over  of dimension
of dimension 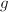 and degree
and degree 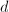 . Let
. Let 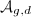 be the Siegel modular variety with its canonical projective embedding. Then associated with
be the Siegel modular variety with its canonical projective embedding. Then associated with 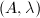 we have a point
we have a point 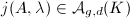 .We define the modular height of
.We define the modular height of 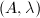 to be
to be 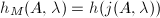 .
.
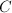 be a constant. Then there are only finitely many isomorphism classes of polarized abelian varieties
be a constant. Then there are only finitely many isomorphism classes of polarized abelian varieties 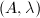 over
over  of dimension
of dimension 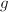 , degree
, degree 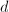 having semistable reduction everywhere and
having semistable reduction everywhere and 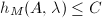 .
.
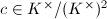 ,
, 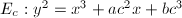 are all isomorphic over
are all isomorphic over 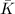 but not isomorphic over
but not isomorphic over  . These
. These 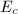 's have the same
's have the same 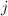 -invariant, hence
-invariant, hence 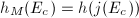 are the same.
are the same.
To clarify the proof, we recall the following lemma without proof.
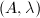 be a polarized abelian variety. Then
be a polarized abelian variety. Then
- The group of automorphisms
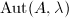 is finite.
is finite. - Suppose
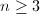 , an automorphism of
, an automorphism of 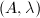 acting on
acting on 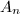 trivially must be the identity.
trivially must be the identity.
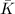 -isomorphism classes of such
-isomorphism classes of such 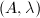 is finite. So we need to show that given a polarized abelian variety
is finite. So we need to show that given a polarized abelian variety 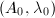 with semistable reduction everywhere, there are only finitely many
with semistable reduction everywhere, there are only finitely many  -isomorphism classes
-isomorphism classes 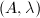 with semistable reduction everywhere which are isomorphic to
with semistable reduction everywhere which are isomorphic to 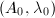 over
over 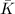 . We shall show that there exists a finite extension
. We shall show that there exists a finite extension 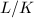 such that all these
such that all these 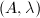 are actually isomorphic to
are actually isomorphic to 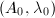 over
over 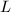 . Then
. Then 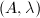 's are parametrized by
's are parametrized by 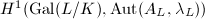 , which is finite, since
, which is finite, since 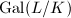 and
and 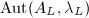 (by the previous lemma) are finite. This completes the proof.
(by the previous lemma) are finite. This completes the proof.
It remains to construct such an 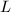 . Because
. Because 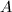 ,
, 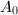 have semistable reduction everywhere and they are isomorphic over a finite extension of
have semistable reduction everywhere and they are isomorphic over a finite extension of  , we know that
, we know that 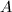 ,
, 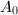 have the same set
have the same set 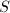 of places of bad reduction. Fix a prime
of places of bad reduction. Fix a prime 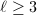 , then
, then 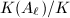 is an extension of degree
is an extension of degree 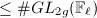 and is unramified outside
and is unramified outside 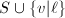 by Neron-Ogg-Shafarevich's criterion. Therefore by Hermite's theorem, the compositum field
by Neron-Ogg-Shafarevich's criterion. Therefore by Hermite's theorem, the compositum field 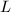 of all
of all 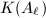 's must be a finite extension of
's must be a finite extension of  . We claim that all
. We claim that all 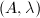 's are isomorphic to
's are isomorphic to 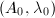 over
over 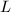 . Let
. Let 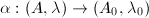 be an isomorphism over
be an isomorphism over 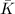 . Then for any
. Then for any 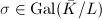 ,
, 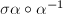 is an automorphism of
is an automorphism of 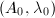 which leaves
which leaves 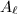 fixed, therefore is the identity by the previous lemma. So the isomorphism
fixed, therefore is the identity by the previous lemma. So the isomorphism 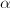 is actually defined over
is actually defined over 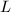 .
¡õ
.
¡õ
It would be wonderful to show Height II for the modular height, unfortunately, it is not clear how 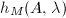 changes under isogeny. Faltings introduced what is now known as the Faltings height
changes under isogeny. Faltings introduced what is now known as the Faltings height 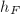 to attack Finiteness II. It turns out miraculously that the Faltings height can be proved to change only slightly under isogeny, and thus Height II is true for
to attack Finiteness II. It turns out miraculously that the Faltings height can be proved to change only slightly under isogeny, and thus Height II is true for 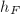 . More precisely,
. More precisely,
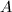 be an abelian variety over
be an abelian variety over  having semistable reduction everywhere. Then
having semistable reduction everywhere. Then 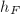 is bounded in the isogeny class of
is bounded in the isogeny class of 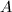 .
.
Finally, to combine the Height I result for 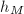 and Height II result for
and Height II result for 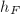 , one needs a comparison theorem between
, one needs a comparison theorem between 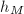 and
and 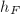 : the boundedness of one of them implies the boundedness of the other.
: the boundedness of one of them implies the boundedness of the other.
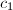 ,
, 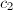 ,
, 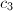 such that for abelian varieties
such that for abelian varieties 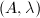 over
over  with semistable reduction everywhere,
with semistable reduction everywhere, 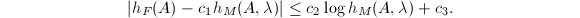
Now the road-map for proving Finiteness I is
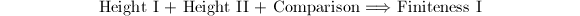
Height II (using the results of Raynaud and Tate on 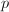 -divisible groups) and the comparison theorem (using the compactified Siegel modular variety over
-divisible groups) and the comparison theorem (using the compactified Siegel modular variety over 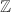 ) are the hardest parts of the whole proof and will occupy most of the remaining semester. In the rest of this talk, I will prove the comparison theorem for the case of elliptic curves, to somehow convince you that it is a reasonable thing to expect. If time permits, I will show Finiteness I for elliptic curves using a different argument, taking advantage of Siegel's theorem on integral points on elliptic curves.
) are the hardest parts of the whole proof and will occupy most of the remaining semester. In the rest of this talk, I will prove the comparison theorem for the case of elliptic curves, to somehow convince you that it is a reasonable thing to expect. If time permits, I will show Finiteness I for elliptic curves using a different argument, taking advantage of Siegel's theorem on integral points on elliptic curves.
 Metrized line bundles and the Faltings height
Metrized line bundles and the Faltings height
We shall now motivate the definition of the Faltings height, which already showed up in Dick's introduction and also in Carl's talk. Suppose we have a complex elliptic curve 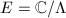 for some period lattice
for some period lattice 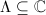 . Intuitively,
. Intuitively, 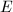 is more complicated if
is more complicated if 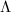 is more complicated, so we may attempt to define the height of
is more complicated, so we may attempt to define the height of 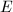 as
as 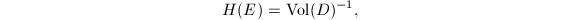 where
where 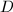 is the fundamental domain for
is the fundamental domain for 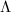 . However, this quantity is not well defined for a given isomorphism class: for example, scaling
. However, this quantity is not well defined for a given isomorphism class: for example, scaling 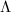 gives isomorphic elliptic curves, but
gives isomorphic elliptic curves, but 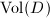 is different. Notice that fixing the period lattice is equivalent to fixing a canonical choice for a differential
is different. Notice that fixing the period lattice is equivalent to fixing a canonical choice for a differential 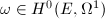 :
: 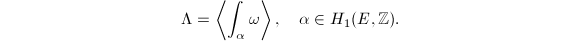 If
If 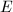 is defined over
is defined over 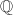 , this canonical choice can be made using the minimal Weierstrass equation
, this canonical choice can be made using the minimal Weierstrass equation 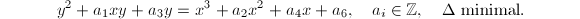 The differential
The differential 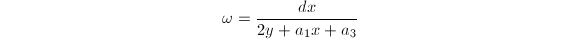 is then well defined up to multiplication by
is then well defined up to multiplication by 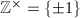 and the period lattice is uniquely determined by the isomorphism class of
and the period lattice is uniquely determined by the isomorphism class of 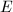 . In this case,
. In this case, 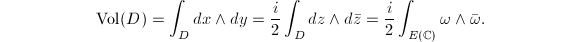
We are using the crucial fact that 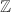 is a PID to define the minimal Weierstrass equation. In general, for
is a PID to define the minimal Weierstrass equation. In general, for 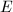 defined over a number field
defined over a number field  , its ring of integers
, its ring of integers 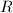 is not necessarily a PID and a minimal Weierstrass equation does not exist. To obtain a canonical choice of the differential, we need the Neron models George talked about last time. Let
is not necessarily a PID and a minimal Weierstrass equation does not exist. To obtain a canonical choice of the differential, we need the Neron models George talked about last time. Let 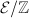 be the Neron model of
be the Neron model of 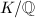 . Then the sheaf of Neron differentials
. Then the sheaf of Neron differentials 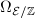 is locally free of rank 1. So the pull back
is locally free of rank 1. So the pull back 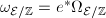 by the zero section
by the zero section 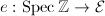 gives us a projective
gives us a projective 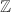 - module of rank 1. Because
- module of rank 1. Because 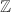 is a PID, this module is actually a free module of rank 1. Therefore it has a canonical generator up to sign, which is exactly the above differential
is a PID, this module is actually a free module of rank 1. Therefore it has a canonical generator up to sign, which is exactly the above differential 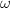 . For a number field
. For a number field  , the same construction gives a projective
, the same construction gives a projective 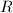 -module of rank 1, where
-module of rank 1, where 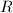 is the ring of integers of
is the ring of integers of  . When
. When 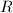 is not a PID,
is not a PID, 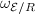 is not necessarily free and we cannot take a global generator, but only a bunch of local generators for each finite place. This motivates us to define the notion of metrized line bundles, introduced by Arakelov.
is not necessarily free and we cannot take a global generator, but only a bunch of local generators for each finite place. This motivates us to define the notion of metrized line bundles, introduced by Arakelov.
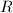 be the ring of integers of
be the ring of integers of  . A metrized line bundle on
. A metrized line bundle on 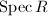 is a pair
is a pair 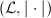 , where
, where 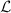 is a line bundle on
is a line bundle on 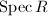 (i.e. a projective
(i.e. a projective 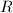 -module of rank 1) and for each
-module of rank 1) and for each 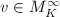 ,
, 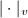 is a norm on the real or complex vector space
is a norm on the real or complex vector space 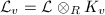 .
.
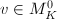 , suppose
, suppose 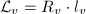 , we set
, we set 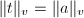 if
if 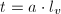 for
for 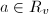 . For
. For 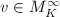 , we denote
, we denote 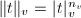 . The height of a metrized line bundle
. The height of a metrized line bundle 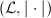 is defined to be
is defined to be 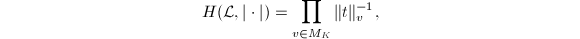 for any
for any 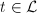 . It is well-defined by the product formula. The degree of
. It is well-defined by the product formula. The degree of 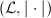 is defined to be
is defined to be 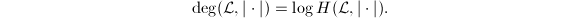
![$[\mathcal{L}:Rt]$](./latex/latex2png-HeightsAndFiniteness_80274248_-5.gif) . When
. When 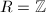 and
and 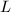 is the generator of
is the generator of 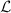 , one then recovers that
, one then recovers that 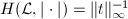 (one thinks of
(one thinks of 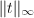 as the area
as the area 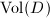 ).
).
Now let us come back to the case of abelian varieties. Let 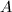 be an abelian variety of dimension
be an abelian variety of dimension 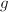 over
over  . Let
. Let 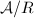 be the Neron model of
be the Neron model of 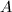 . Then the sheaf of Neron differentials
. Then the sheaf of Neron differentials 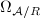 is locally free of rank
is locally free of rank 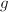 on
on 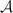 . So the top wedge power
. So the top wedge power 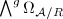 is a locally free sheaf of rank 1 on
is a locally free sheaf of rank 1 on 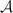 . Pulling back by the zero section
. Pulling back by the zero section 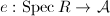 , we obtain a line bundle
, we obtain a line bundle 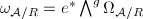 . We specify the norm for every
. We specify the norm for every 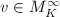 by
by 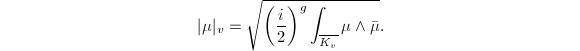
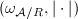 be the metrized line bundle on
be the metrized line bundle on  described above. The Faltings height of
described above. The Faltings height of 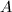 is defined to be
is defined to be ![$$h_F(A)=\frac{1}{[K:\mathbb{Q}]}\deg (\mathcal{L},|\cdot|).$$](./latex/latex2png-HeightsAndFiniteness_83143373_.gif)
 . However, by the semistable stable reduction theorem, the Neron model does not change after base change to some finite field extension. We thus define the stable Faltings height to be the Faltings height
. However, by the semistable stable reduction theorem, the Neron model does not change after base change to some finite field extension. We thus define the stable Faltings height to be the Faltings height 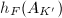 , for any
, for any  such that
such that  has semistable stable reduction everywhere.
has semistable stable reduction everywhere.
 Comparison of heights for elliptic curves
Comparison of heights for elliptic curves
We first give an explicit formula of the Faltings height 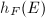 .
.
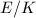 be an elliptic curve. Suppose
be an elliptic curve. Suppose 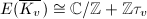 for
for 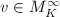 . Then
. Then ![$$h_F(E)=\frac{1}{12[K:\mathbb{Q}]}\left(\log|\mathbb{N}_{K/\mathbb{Q}}\Delta_{E/K}|-\sum_{v\in M_K^\infty}n_v\log\left(|\Delta(\tau_v)|(\Im \tau_v)^6\right)\right),$$](./latex/latex2png-HeightsAndFiniteness_236917916_.gif) where
where 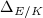 is the minimal discriminant and
is the minimal discriminant and 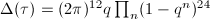 is the modular discriminant function.
is the modular discriminant function.
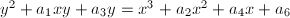 be any Weierstrass equation of
be any Weierstrass equation of 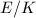 . We shall utilize the invariance of the section
. We shall utilize the invariance of the section 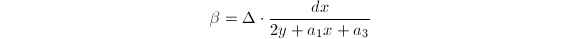 of
of 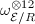 under the change of coordinates to calculate the Faltings height locally. For
under the change of coordinates to calculate the Faltings height locally. For 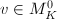 , let
, let 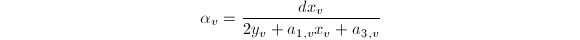 be the Neron differential at
be the Neron differential at  , then by the invariance of
, then by the invariance of 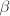 , we know that
, we know that 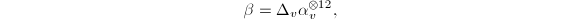 where
where 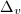 is the minimal discriminant of
is the minimal discriminant of 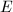 at
at  . So for
. So for 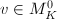 ,
, 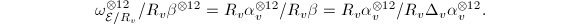 Hence the local contribution at
Hence the local contribution at  is
is 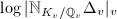 and the total nonarchimedean contribution is
and the total nonarchimedean contribution is 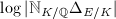 . For
. For 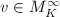 , let
, let 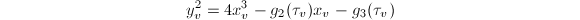 be the Weierstrass equation given by
be the Weierstrass equation given by 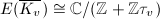 and
and 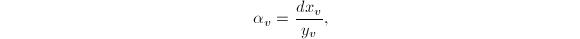 then by the invariance of
then by the invariance of 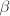 , we know that
, we know that 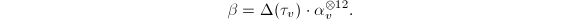 We compute
We compute 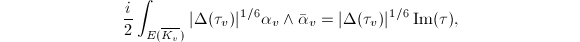 therefore the local contribution at
therefore the local contribution at  is
is ![$$\frac{n_v}{[K:\mathbb{Q}]}\log \left(|\Delta(\tau_v)|^{1/6}\Im\tau_v\right)^{1/2},$$](./latex/latex2png-HeightsAndFiniteness_13383407_.gif) and the total archimedean contribution is
and the total archimedean contribution is ![$$\frac{1}{12[K:\mathbb{Q}]}\sum_{v\in M_K^\infty}n_v\log\left(|\Delta(\tau_v)|(\Im \tau_v)^6\right).$$](./latex/latex2png-HeightsAndFiniteness_106003929_.gif) This completes the proof.
¡õ
This completes the proof.
¡õ
Using the previous explicit expression, now we can prove the comparison theorem of the Faltings height and the modular height for elliptic curves.
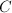 such that for elliptic curves
such that for elliptic curves 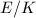 with semistable reduction everywhere,
with semistable reduction everywhere, 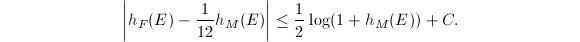
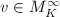 , we can suitably choose
, we can suitably choose 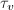 such that
such that 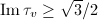 , so that
, so that 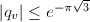 . Hence
. Hence 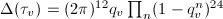 implies that
implies that 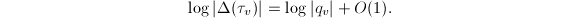 Using the
Using the 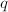 -expansion of
-expansion of 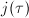 , one also knows that
, one also knows that 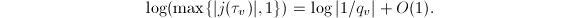 Therefore
Therefore 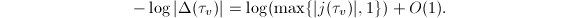 Also from
Also from 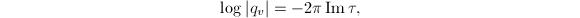 we obtain
we obtain 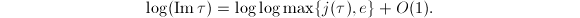 Plugging into the explicit formula of the Faltings height gives
Plugging into the explicit formula of the Faltings height gives
![\begin{equation*}
\begin{split}
h_F(E)=\frac{1}{12[K:\mathbb{Q}]}\Big(\log|\mathbb{N}_{K/\mathbb{Q}}\Delta_{E/K}|+\sum_{v\in M_K^\infty}n_v\big(\log \max\{|j(E)|_v,1\}\\-6\log\log\max\{|j(\tau)|_v,e\}+O(1)\big)\Big).
\end{split}
\end{equation*}](./latex/latex2png-HeightsAndFiniteness_194158782_.gif)
Since  has semistable reduction everywhere, we know that
has semistable reduction everywhere, we know that 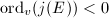 if and only if
if and only if  dividing
dividing 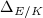 and in this case
and in this case 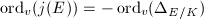 . Thus
. Thus ![$$\log|\mathbb{N}_{K/\mathbb{Q}}\Delta_{E/K}|+\sum_{v\in M_K^\infty}n_v\log \max\{|j(E)|_v,1\}=\log H_K(j(E))=[K:\mathbb{Q}]h(j(E)).$$](./latex/latex2png-HeightsAndFiniteness_97153221_.gif) So it remains to show that
So it remains to show that ![$$\sum_{v\in M_K^\infty}\log\log\max\{|j(\tau)|_v,e\}\le [K:\mathbb{Q}]\log(1+h(j(E))), $$](./latex/latex2png-HeightsAndFiniteness_147020577_.gif) which I shall leave it as an exercise using the arithmetic-geometric mean inequality.
¡õ
which I shall leave it as an exercise using the arithmetic-geometric mean inequality.
¡õ
 Finiteness theorems for elliptic curves
Finiteness theorems for elliptic curves
Finally, we shall utilize Siegel's theorem on the integral points of elliptic curves to give a completely different direct proof of Finiteness I for elliptic curves.
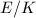 be an (affine) elliptic curve,
be an (affine) elliptic curve, 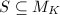 be a finite set containing
be a finite set containing 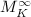 and
and 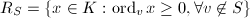 be the ring of
be the ring of 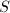 -integers. Then the set of integral points
-integers. Then the set of integral points 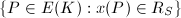 is finite.
is finite.
Siegel's proof uses techniques from Diophantine approximations, which we do not get into here. We will deduce Finiteness I from the even stronger Shafarevich's theorem for elliptic curves. The following cute proof is due to Shafarevich.
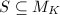 be a finite set containing
be a finite set containing 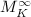 . Then there are only finitely many isomorphism classes
. Then there are only finitely many isomorphism classes 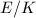 having good reduction outside
having good reduction outside 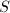 .
.
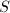 so that
so that 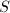 contains all places over 2 and 3 and also
contains all places over 2 and 3 and also 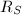 is a PID. Then for every
is a PID. Then for every 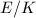 , we have a minimal Weierstrass equation
, we have a minimal Weierstrass equation 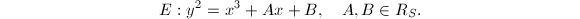 If further
If further 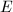 has good reduction outside
has good reduction outside 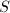 , we know the discriminant
, we know the discriminant 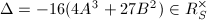 . Suppose we have an infinite sequence of elliptic curves
. Suppose we have an infinite sequence of elliptic curves 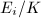 having good reduction outside
having good reduction outside 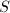 . Since the
. Since the 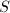 -unit group
-unit group 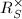 is finitely generated, we know that
is finitely generated, we know that 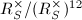 is a finite group. So we can find an infinite subsequence (still denoted by
is a finite group. So we can find an infinite subsequence (still denoted by 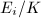 ), such that
), such that 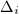 are in the same class of
are in the same class of 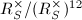 . In other words,
. In other words, 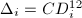 for a fixed
for a fixed 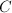 . From
. From 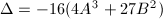 , we know that
, we know that 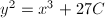 has
has 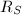 -solutions
-solutions 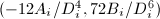 . Therefore by Siegel's theorem, there are only finitely many possibilities for
. Therefore by Siegel's theorem, there are only finitely many possibilities for 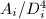 and
and 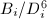 . Moreover, each of the identities
. Moreover, each of the identities 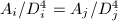 ,
, 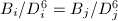 gives a
gives a  -isomorphism
-isomorphism  via
via 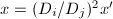 ,
, 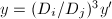 .
¡õ
.
¡õ
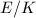 . Then there are only finitely many elliptic curves
. Then there are only finitely many elliptic curves 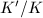 which are isogenous to
which are isogenous to 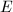 .
.
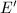 and
and 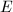 are isogenous over
are isogenous over  . Then they have the same set of places of good reduction by Neron-Ogg-Shafarevich (the induced map
. Then they have the same set of places of good reduction by Neron-Ogg-Shafarevich (the induced map ![$E'[m]\rightarrow E[m]$](./latex/latex2png-HeightsAndFiniteness_255947009_-5.gif) is an isomorphism of
is an isomorphism of 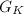 -modules for all
-modules for all 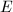 's prime to the characteristic of the residue field and the degree of the isogeny). The result then follows from Shafarevich's theorem.
¡õ
's prime to the characteristic of the residue field and the degree of the isogeny). The result then follows from Shafarevich's theorem.
¡õ
References
[1]Heights and elliptic curves, Arithmetic geometry (Storrs, Conn., 1984), Springer, 1986, 253--265.
[2]Abelian Varieties (v2.00), Available at www.jmilne.org/math/.
[3]The Arithmetic of Elliptic Curves (Graduate Texts in Mathematics), Springer, 2010.
[4]Heights in Diophantine Geometry (New Mathematical Monographs), Cambridge University Press, 2007.
[5]Diophantine Geometry: An Introduction (Graduate Texts in Mathematics), Springer, 2000.
![$x=[a,b]\in \mathbb{P}^1(K)$](./latex/latex2png-HeightsAndFiniteness_95009199_-5.gif) , we define the relative height
, we define the relative height 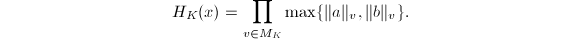
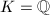 , in that case
, in that case 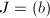 and
and 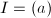 .
.
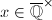 . Then
. Then 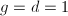 , the modular height of an elliptic curve is simply the height of its
, the modular height of an elliptic curve is simply the height of its 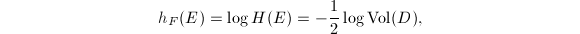 which coincides with our intuition.
which coincides with our intuition.
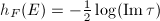 for the minimal Weierstrass equation
for the minimal Weierstrass equation 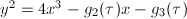 .
.