- Deformations of Galois representations
- Group-theoretic hypothesis
-
Liftings of mod
 representations
representations
- Some background on irreducible representations
-
Deformations of mod
 representations
representations
- Linear algebraic lemmas
- Tangent spaces
- Generic fiber of universal lifting rings
- Deformation problems
- Global Galois deformation problems
- Presenting global deformation rings over local lifting rings
-
Computation of
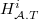
-
Local universal lifting rings
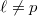
-
Local universal lifting rings
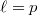
These are my live-TeXed notes for the course 18.786: Galois Representations taught by Sug Woo Shin at MIT, Spring 2014. References.
Any mistakes are the fault of the notetaker. Let me know if you notice any mistakes or have any comments!
02/25/2014
 Deformations of Galois representations
Deformations of Galois representations
The global Langlands correspondence is roughly a correspondence between automorphic forms (representations) and  -adic Galois representations. Suppose we are given the arrow automorphic representations
-adic Galois representations. Suppose we are given the arrow automorphic representations 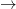
 -adic Galois representations (of course this is highly nontrivial), then it is relatively easy to show this arrow is injective. The strategy to show that this is also surjective (modularity of Galois representations
-adic Galois representations (of course this is highly nontrivial), then it is relatively easy to show this arrow is injective. The strategy to show that this is also surjective (modularity of Galois representations  ) is to first show that the reduction
) is to first show that the reduction 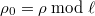 is the reduction of the Galois representation
is the reduction of the Galois representation  coming from a modular form
coming from a modular form  (this is Serre's conjecture in general), then try to study infinitesimal liftings
(this is Serre's conjecture in general), then try to study infinitesimal liftings 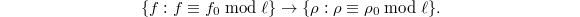 Now both sides then have more algebro-geometric structures (like a map of schemes
Now both sides then have more algebro-geometric structures (like a map of schemes 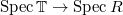 ). It often turns out to be a closed immersion. If one can then show (e.g., by dimension reason) this is actually an isomorphism (
). It often turns out to be a closed immersion. If one can then show (e.g., by dimension reason) this is actually an isomorphism (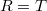 theorem), then the surjectivity will follow. Our goal in next few lectures is to study the right hand side, the deformations of Galois representations.
theorem), then the surjectivity will follow. Our goal in next few lectures is to study the right hand side, the deformations of Galois representations.
 Group-theoretic hypothesis
Group-theoretic hypothesis
When deforming a representation 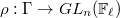 , we would like to impose a finiteness condition on the profinite
, we would like to impose a finiteness condition on the profinite 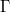 , in order to make sense of the the space of deformations and make ring
, in order to make sense of the the space of deformations and make ring 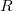 noetherian. Fix
noetherian. Fix  a prime and
a prime and 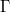 a profinite group. We impose the following
a profinite group. We impose the following  -finiteness assumption.
-finiteness assumption.
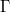 ): for any
): for any 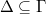 an open finite index subgroup,
an open finite index subgroup,
![$\Delta/\langle[\Delta,\Delta],\Delta^\ell\rangle$](./latex/latex2png-GaloisRepresentations_120802874_-5.gif) is finite ( =
is finite ( = 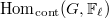 is finite dimensional over
is finite dimensional over 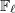 ). Here
). Here 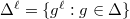 .
.- The maximal pro-
 quotient of
quotient of 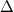 is topologically finitely generated (i.e., there exists a finitely generated dense subgroup).
is topologically finitely generated (i.e., there exists a finitely generated dense subgroup).
 is topologically finitely generated, any finite index subgroup
is topologically finitely generated, any finite index subgroup  is automatically open. This may fail for groups like
is automatically open. This may fail for groups like  .
.
- Use Burnside basis theorem (see [Boe] Ex 1.8.1).
- The same generator for
 will work for the maximal pro-
will work for the maximal pro- quotient of
quotient of 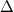 .
¡õ
.
¡õ
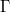 is topologically finitely generated, then any
is topologically finitely generated, then any 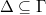 of finite index is also topologically finitely generated.
of finite index is also topologically finitely generated.
- Let
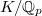 be a finite extension (
be a finite extension (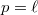 or
or 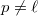 ) Then
) Then 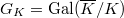 satisfies Hyp: to check a), it is the same thing to check that there exists only finitely many abelian extension of exponent
satisfies Hyp: to check a), it is the same thing to check that there exists only finitely many abelian extension of exponent  for a given local field. This follows from Kummer theory.
for a given local field. This follows from Kummer theory. - Let
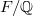 be a finite extension,
be a finite extension, 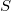 be a finite set of finite places of
be a finite set of finite places of 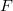 ,
, 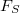 be the maximal extension of
be the maximal extension of 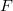 unramified outside
unramified outside  . Then
. Then  satisfies Hyp (by global class field theory, see [DDT] 2.41 for details). Notice that
satisfies Hyp (by global class field theory, see [DDT] 2.41 for details). Notice that  itself is not known to be topologically finitely generated.
itself is not known to be topologically finitely generated.
 Liftings of mod
Liftings of mod  representations
representations
Let 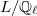 be a finite extension,
be a finite extension, 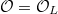 with uniformizer
with uniformizer 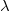 and residue field
and residue field 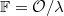 .
.
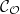 be the following category. The objects of
be the following category. The objects of 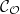 are complete noetherian local
are complete noetherian local 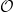 -algebras
-algebras 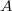 such that
such that 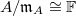 . Here
. Here 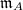 is the unique maximal ideal of
is the unique maximal ideal of 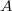 and the completeness means that
and the completeness means that 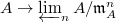 is an isomorphism. Notice the
is an isomorphism. Notice the  -algebra isomorphism
-algebra isomorphism 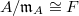 is unique if it exists.
is unique if it exists.
The morphisms in 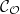 are morphisms of local
are morphisms of local  -algebras
-algebras 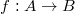 (i.e.,
(i.e., 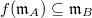 ). It follows that
). It follows that  induces an isomorphism
induces an isomorphism  .
.
 -algebra morphism
-algebra morphism 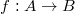 between
between 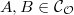 is automatically local: since
is automatically local: since 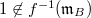 ,
, 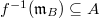 is proper ideal. Hence
is proper ideal. Hence 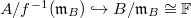 is a nonzero subring, so
is a nonzero subring, so 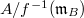 must be a field. Therefore
must be a field. Therefore 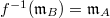 .
.
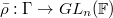 be a continuous representation. Define
be a continuous representation. Define 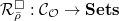 given by
given by 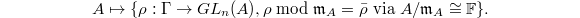 This is a functor and is called the liftings of
This is a functor and is called the liftings of 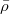 .
.
 is involved in the definition! In Kisin's terminology,
is involved in the definition! In Kisin's terminology, 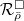 is called the framed deformations of
is called the framed deformations of 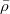 , which somehow explains the
, which somehow explains the  in the notation.
in the notation.
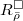 the universal lifting ring of
the universal lifting ring of 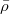 . Explicitly, this means that
. Explicitly, this means that 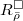 satisfies one of the following equivalent conditions:
satisfies one of the following equivalent conditions:
- There are bijections
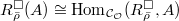 , functorial in
, functorial in 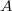 .
. - There exists a universal lifting
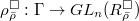 of
of 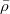 such that for any
such that for any 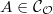 and a lifting
and a lifting 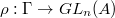 , there exists a unique
, there exists a unique 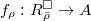 such that
such that 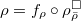
 . Giving
. Giving 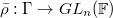 is the same as giving an element
is the same as giving an element 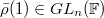 . Fix a lift
. Fix a lift 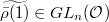 . Then
. Then  is in bijection with
is in bijection with 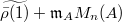 , given by
, given by 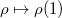 . Hence
. Hence ![$$\mathcal{R}^\Box_{\bar\rho}(A)\cong\mathfrak{m}_A^{n^2}\cong\Hom_{\mathcal{C}_\mathcal{O}}(\mathcal{O}[ [X_{i,j}] ]_{i,j=1}^n, A).$$](./latex/latex2png-GaloisRepresentations_32344580_.gif) So
So ![$\mathcal{O}[ [ X_{i,j}] ]_{i,j=1}^n$](./latex/latex2png-GaloisRepresentations_196908519_-6.gif) represents
represents 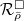 .
.
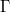 ), one may assume that
), one may assume that 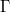 is topologically finitely generated.
is topologically finitely generated.
In fact, let 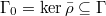 (an open finite index subgroup). Let
(an open finite index subgroup). Let 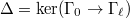 , here
, here 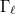 is the maximal pro-
is the maximal pro- quotient of
quotient of 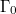 . We claim that one may replace
. We claim that one may replace 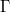 with
with 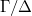 . Then
. Then 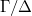 is topologically finitely generated profinite group (though
is topologically finitely generated profinite group (though 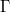 may not be): look at the exact sequence
may not be): look at the exact sequence 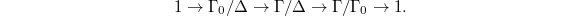 Notice
Notice 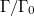 is finite and
is finite and 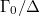 is topologically finitely generated by Hyp(
is topologically finitely generated by Hyp( ). It follows that
). It follows that  is also topologically finitely generated.
is also topologically finitely generated.
The key thing is that every lifting of  factors through
factors through  . Indeed, Suppose
. Indeed, Suppose 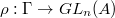 is such a lifting. Since
is such a lifting. Since 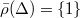 , we know that
, we know that 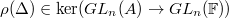 , this kernel is pro-
, this kernel is pro- , but by construction
, but by construction 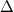 is prime-to-
is prime-to- . Hence
. Hence 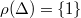 and we may replace
and we may replace 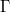 with
with 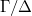 .
.
Step 2 Let 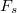 be the free group on
be the free group on  generators
generators 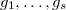 and
and 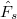 be the profinite completion of
be the profinite completion of 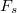 . One can choose
. One can choose  so that there is a surjection
so that there is a surjection 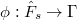 . Let
. Let 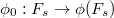 be the restriction to the dense subgroup
be the restriction to the dense subgroup 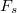 . Let
. Let 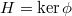 and
and 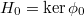 . One can check that
. One can check that 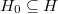 is also dense. Now giving a lifting
is also dense. Now giving a lifting 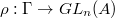 is the same as giving
is the same as giving 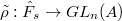 (i.e.
(i.e. 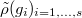 ) being trivial on
) being trivial on 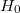 . Now
. Now 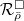 is represented by
is represented by ![$\mathcal{O}[ [X_{i,j}^k] ]_{i,j=1}^n{}_{k=1}^s/\{\text{relations from }H_0\}$](./latex/latex2png-GaloisRepresentations_229055668_-6.gif) .
¡õ
.
¡õ
02/27/2014
 Some background on irreducible representations
Some background on irreducible representations
We switch notations temperately. Let 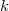 be a field,
be a field, 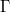 be an abstract group,
be an abstract group, 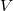 be an finite dimensional
be an finite dimensional 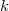 -vector spaces. Recall that
-vector spaces. Recall that 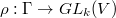 is irreducible if there is no proper
is irreducible if there is no proper 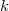 -subvector space which is
-subvector space which is 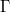 -stable.
-stable.
![$\alpha\in\End_{k[\Gamma]}(\rho)$](./latex/latex2png-GaloisRepresentations_73738464_-6.gif) is nonzero, then
is nonzero, then 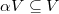 is nonzero and
is nonzero and  -stable, hence
-stable, hence  . Therefore
. Therefore  is invertible.
¡õ
is invertible.
¡õ
 is irreducible does not imply that
is irreducible does not imply that 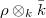 is irreducible. A division algebra over
is irreducible. A division algebra over 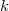 may not be a division algebra when extending scalars to
may not be a division algebra when extending scalars to 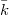 .
.
![$\End_{k[\Gamma]}(\rho)=k$](./latex/latex2png-GaloisRepresentations_201823886_-6.gif) does not imply that
does not imply that  is irreducible. For example, consider the non-semisimple representation
is irreducible. For example, consider the non-semisimple representation 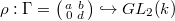 . Then
. Then ![$\End_{k[\Gamma]}(\rho)=k$](./latex/latex2png-GaloisRepresentations_201823886_-6.gif) but
but  is clearly reducible.
is clearly reducible.
 is Schur, if
is Schur, if ![$\End_{k[\Gamma]}(\rho)=k$](./latex/latex2png-GaloisRepresentations_201823886_-6.gif) ; absolutely irreducible if for any
; absolutely irreducible if for any 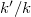 a field extension,
a field extension, 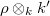 is irreducible.
is irreducible.
 is absolutely irreducible if and only if
is absolutely irreducible if and only if 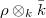 is irreducible, if and only if
is irreducible, if and only if  is irreducible and Schur.
is irreducible and Schur.
 Deformations of mod
Deformations of mod  representations
representations
We are back to the usual notation as in the section of lifting of mod  representations.
representations.
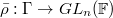 be a continuous representation. We define
be a continuous representation. We define  the functor of deformations of
the functor of deformations of 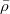 by
by 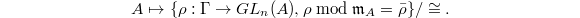 Here
Here  if there exists
if there exists 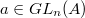 such that
such that 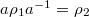 . When
. When 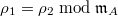 , this happens if and only if
, this happens if and only if  can be chosen in
can be chosen in 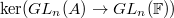 .
.
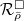 (see [DDT] 2.36). Kisin's approach, roughly speaking, is to show that
(see [DDT] 2.36). Kisin's approach, roughly speaking, is to show that 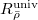 is the geometric quotient of
is the geometric quotient of 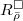 by
by 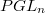 (see [Boe] 2.1). Also see [Maz97] 10.
¡õ
(see [Boe] 2.1). Also see [Maz97] 10.
¡õ
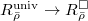 . It is induced by the functor
. It is induced by the functor 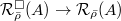 by sending
by sending  to its isomorphism class. Another way: view
to its isomorphism class. Another way: view 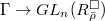 as a deformation. We will see more precise descriptions later.
as a deformation. We will see more precise descriptions later.
 Linear algebraic lemmas
Linear algebraic lemmas
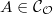 ,
, 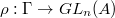 be a continuous representation. Assume
be a continuous representation. Assume 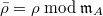 is absolutely irreducible.
is absolutely irreducible.
- (Schur for
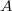 -coefficient) For
-coefficient) For 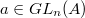 , if
, if 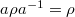 , then
, then 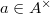 .
. - (Carayol's Lemma) Suppose
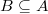 (in
(in 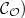 is closed and
is closed and 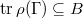 . Then there exists
. Then there exists 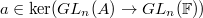 such that
such that 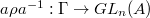 factors through
factors through 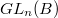 .
.
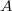 is Artinian local
is Artinian local 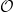 -algebra (since
-algebra (since 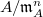 are of this shape). Then induct on the length of
are of this shape). Then induct on the length of 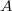 . The case
. The case  is easy and one can further reduce to the case
is easy and one can further reduce to the case ![$A=\mathbb{F}[\varepsilon]/(\varepsilon^2)$](./latex/latex2png-GaloisRepresentations_57364708_-5.gif) .
.
- Assume
 . Choose a minimal nonzero ideal
. Choose a minimal nonzero ideal 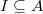 : one has the filtration
: one has the filtration 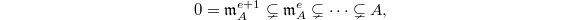 where
where 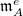 is a
is a  -vector space; one can choose
-vector space; one can choose 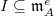 to be isomorphic to
to be isomorphic to 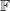 as an
as an 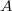 -module. Let
-module. Let 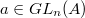 such that
such that  . Then the induction hypothesis implies that
. Then the induction hypothesis implies that  . So we can write
. So we can write  , where
, where  and
and 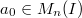 . Now the equation
. Now the equation 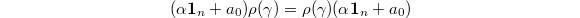 tells us that
tells us that 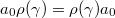 in
in 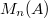 . Under the identification
. Under the identification 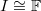 , we find that
, we find that 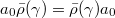 in
in 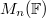 , hence by Schur's lemma,
, hence by Schur's lemma, 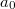 itself must be a scalar too (we only need
itself must be a scalar too (we only need  to be Schur in this part).
to be Schur in this part). - By induction hypothesis, we may assume that
 lands in
lands in  . Since
. Since  as
as 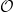 -submodules, we know that either
-submodules, we know that either 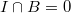 or
or 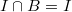 . In the latter case, it is immediate that
. In the latter case, it is immediate that  lands in
lands in 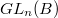 . The first case is more difficult. We build the
. The first case is more difficult. We build the 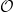 -algebra
-algebra 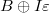 , where
, where 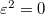 . Then
. Then 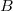 embeds into
embeds into 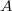 by
by 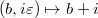 . By induction hypothesis, we may assume
. By induction hypothesis, we may assume 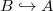 is indeed an isomorphism. We may replace
is indeed an isomorphism. We may replace 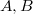 by
by 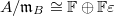 and
and 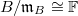 (because quotient by any thing in
(because quotient by any thing in 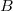 is fine). This is a much more concrete problem and the rest of the proof can be found in [CHT] Lemma 2.1.10. Here is roughly how it works. Extend
is fine). This is a much more concrete problem and the rest of the proof can be found in [CHT] Lemma 2.1.10. Here is roughly how it works. Extend ![$\rho: \Gamma\rightarrow \mathbb{F}[\varepsilon]/\varepsilon^2$](./latex/latex2png-GaloisRepresentations_170117944_-5.gif)
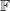 -linearly and we obtain that
-linearly and we obtain that ![$\rho: \mathbb{F}[\Gamma]\rightarrow M_n(\mathbb{F})\oplus M_n(\mathbb{F})\varepsilon$](./latex/latex2png-GaloisRepresentations_105402247_-5.gif) ,
, 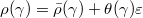 . Here
. Here
![$\theta:\mathbb{F}[\Gamma]\rightarrow M_n(\mathbb{F})$](./latex/latex2png-GaloisRepresentations_184596061_-5.gif) is
is 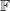 -linear,
-linear,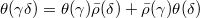 ,
,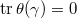 .
.
We want to get rid of 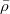 and deal with purely matrix algebra. We claim that
and deal with purely matrix algebra. We claim that 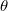 factors through the surjective map
factors through the surjective map ![$\bar\rho: \mathbb{F}[\Gamma]\rightarrow M_n(\mathbb{F})$](./latex/latex2png-GaloisRepresentations_73005711_-5.gif) (here we used the absolutely irreducible assumption for the surjectivity), i.e.,
(here we used the absolutely irreducible assumption for the surjectivity), i.e., 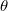 is trivial on
is trivial on 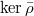 . Let
. Let 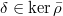 , then
, then 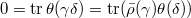 . By the surjectivity of
. By the surjectivity of 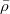 , we know that
, we know that 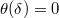 because
because 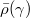 can be anything in
can be anything in 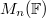 . This proves the claim.
. This proves the claim.
Now we are looking for 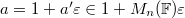 such that
such that 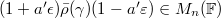 for any
for any 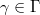 . This is equivalent to that the coefficient of
. This is equivalent to that the coefficient of 
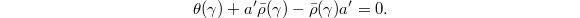 So we are reduced to the problem of showing that for
So we are reduced to the problem of showing that for 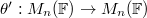 , there exists
, there exists 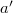 such that
such that
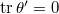 ,
,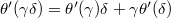 ,
,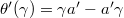 .
.
Conceptually this means that every derivation on 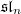 is given by the Lie bracket with some element
is given by the Lie bracket with some element 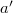 . One can directly show that
. One can directly show that 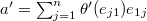 works.
¡õ
works.
¡õ
![$A=\mathbb{F}[\varepsilon]/(\varepsilon^2)$](./latex/latex2png-GaloisRepresentations_57364708_-5.gif) . See [Boe] 2.2.1.
¡õ
. See [Boe] 2.2.1.
¡õ
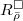 is a power series ring in
is a power series ring in 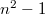 variables over the the universal deformation ring
variables over the the universal deformation ring 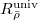 .
.
03/04/2014
 Tangent spaces
Tangent spaces
We are going to work with the universal lifting rings (the same argument works for universal deformation rings). Write 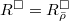 for short. Denote its unique maximal ideal by
for short. Denote its unique maximal ideal by 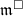 .
.
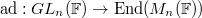 is given by conjugation
is given by conjugation 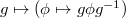 . We denote
. We denote 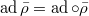 (and the corresponding
(and the corresponding ![$\mathbb{F}[\Gamma]$](./latex/latex2png-GaloisRepresentations_88906499_-5.gif) -module).
-module).
One can analyze the tangent space of  in terms of group cohomology of
in terms of group cohomology of  .
.
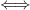 c): by definition.
c): by definition.
a) 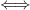 b): Since
b): Since 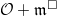 surjects on
surjects on 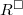 . For
. For 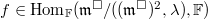 , we define
, we define ![$$R^\Box\rightarrow\mathbb{F}[\varepsilon]/\varepsilon^2\quad, a+x\mapsto \bar a+f(x)\varepsilon.$$](./latex/latex2png-GaloisRepresentations_231435160_.gif) One routinely check that this is well defined (using
One routinely check that this is well defined (using 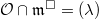 and gives the desired bijection.
and gives the desired bijection.
c) 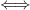 d). Given
d). Given ![$\rho:\Gamma\rightarrow GL_n(\mathbb{F}[\varepsilon]/\varepsilon^2)$](./latex/latex2png-GaloisRepresentations_38338794_-5.gif) , we can write
, we can write 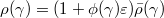 . One can check that
. One can check that  is a homomorphism if and only if
is a homomorphism if and only if 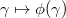 defines a continuous 1-cocycle.
¡õ
defines a continuous 1-cocycle.
¡õ
Write 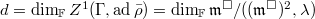 . This is the dimension of cotangent space (ignoring the
. This is the dimension of cotangent space (ignoring the 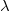 -direction) of
-direction) of 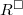 .
.
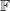 -vector spaces
-vector spaces 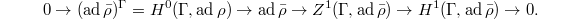 Here any
Here any 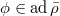 gives the coboundary
gives the coboundary 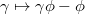 . The result immediately follows.
¡õ
. The result immediately follows.
¡õ
So we can know how big the ring 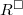 is as long as we know the dimension of
is as long as we know the dimension of 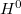 and
and 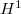 of the adjoint representation.
of the adjoint representation.
This follows from a topological version of Nakayama's lemma. In nice situations, 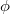 is an isomorphism. In general this is too optimistic but one can further control the the kernel
is an isomorphism. In general this is too optimistic but one can further control the the kernel 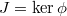 . Notice that
. Notice that 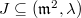 . Here
. Here 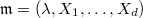 is the maximal ideal of
is the maximal ideal of ![$\mathcal{O}[ [X_1,\ldots, X_d] ]$](./latex/latex2png-GaloisRepresentations_189999498_-5.gif) . We shall construct an injective map
. We shall construct an injective map ![$$\Hom_\mathbb{F}(J/\mathfrak{m}J,\mathbb{F})\rightarrow H^2(\Gamma,\ad\bar\rho),\quad f\mapsto [C_f].$$](./latex/latex2png-GaloisRepresentations_137462282_.gif) When this
When this 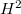 vanishes,
vanishes, 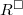 will be an formal power series ring and hence is formally smooth of dimension
will be an formal power series ring and hence is formally smooth of dimension 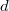 : there is no obstruction for liftings (controlled by
: there is no obstruction for liftings (controlled by 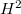 ) and the space of liftings is
) and the space of liftings is 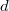 -dimensional (controlled by
-dimensional (controlled by 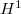 and
and 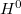 ).
).
To construct ![$f\mapsto [C_f]$](./latex/latex2png-GaloisRepresentations_17802674_-5.gif) , we notice that
, we notice that ![$GL_n(\mathcal{O}[ [X_1,\ldots, X_d] ]/\mathfrak{m}J)\rightarrow GL_n(\mathcal{O}[ [X_1,\ldots, X_d] ]/J)$](./latex/latex2png-GaloisRepresentations_140776487_-5.gif) is surjective. For
is surjective. For 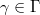 , we can choose a lift
, we can choose a lift 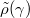 of
of 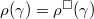 . Notice
. Notice 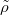 may not be a homomorphism and this failure is measured by
may not be a homomorphism and this failure is measured by 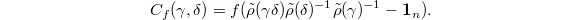 Since
Since 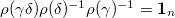 , we know that
, we know that 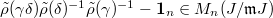 and hence it makes sense to apply
and hence it makes sense to apply 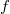 in this expression. One checks directly that
in this expression. One checks directly that 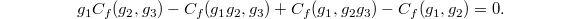 So
So
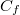 gives a well-defined class
gives a well-defined class ![$[C_f]\in H^2(\Gamma,\ad\bar\rho)$](./latex/latex2png-GaloisRepresentations_219467235_-5.gif) .
.![$[C_f]=0$](./latex/latex2png-GaloisRepresentations_17109925_-5.gif) if and only if there exists a choice of
if and only if there exists a choice of 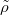 such that
such that 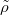 mod
mod 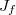 is a homomorphism. Here
is a homomorphism. Here 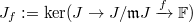 (so
(so 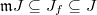 ).
).
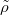 as in b) of the previous exercise, then
as in b) of the previous exercise, then  . Notice
. Notice ![$\mathcal{O}[ [X_1,\ldots, X_d] ]/J_f\twoheadrightarrow \mathcal{O} [[ X_1,\ldots,X_d] ]/J=R^\Box$](./latex/latex2png-GaloisRepresentations_259244193_-5.gif) . Since
. Since 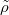 is a lifting of
is a lifting of 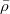 , we have a map
, we have a map ![$$\eta: \mathcal{O} [[ X_1,\ldots,X_d] ]/J\rightarrow \mathcal{O} [[ X_1,\ldots,X_d] ]/J_f$$](./latex/latex2png-GaloisRepresentations_174759622_.gif) by the universal property. The composite map
by the universal property. The composite map ![$$\mathcal{O} [[ X_1,\ldots,X_d] ]/J\xrightarrow{\eta} \mathcal{O} [[ X_1,\ldots,X_d] ]/J_f\twoheadrightarrow \mathcal{O} [[ X_1,\ldots,X_d] ]/J$$](./latex/latex2png-GaloisRepresentations_93773712_.gif) is the identity map. This shows that
is the identity map. This shows that 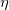 is injective. Let
is injective. Let 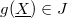 (in particular
(in particular 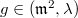 ), we want to show that
), we want to show that 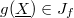 . Suppose
. Suppose 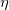 maps
maps 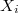 to
to 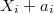 (so
(so 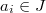 ). One checks directly that
). One checks directly that 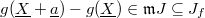 . But
. But 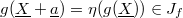 by injectivity, hence
by injectivity, hence 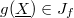 . Therefore so
. Therefore so 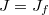 and
and  .
¡õ
.
¡õ
So the number of generators of 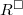 is
is 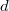 and with the number of relations is equal to
and with the number of relations is equal to 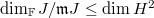 .
.
03/06/2014
 Generic fiber of universal lifting rings
Generic fiber of universal lifting rings
The following is a basic algebraic fact.
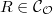 . There is a bijection between closed points of the generic fiber
. There is a bijection between closed points of the generic fiber ![$R[1/\ell]$](./latex/latex2png-GaloisRepresentations_80258974_-5.gif) (these are dense in the generic fiber) and pairs
(these are dense in the generic fiber) and pairs  , where
, where 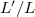 is a finite extension,
is a finite extension, 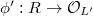 is continuous such that
is continuous such that ![$L'{}=L(\phi'(R[1/\ell]))$](./latex/latex2png-GaloisRepresentations_156666643_-5.gif) .
.
 induces
induces ![$\phi'[/1/\ell]: R[1/\ell]\rightarrow L'$](./latex/latex2png-GaloisRepresentations_12373066_-5.gif) . The kernel of this map is a maximal ideal. This gives the corresponding closed point of the generic fiber. Conversely, any closed point
. The kernel of this map is a maximal ideal. This gives the corresponding closed point of the generic fiber. Conversely, any closed point  with maximal ideal
with maximal ideal 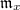 gives rise to
gives rise to ![$\phi_x: R\rightarrow R[1/\ell]\rightarrow R[1/\ell]/\mathfrak{m}_x=L_x$](./latex/latex2png-GaloisRepresentations_110441129_-5.gif) (which factors through
(which factors through 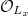 ).
).
Let ![$x\in \Spec R^\Box[1/\ell]$](./latex/latex2png-GaloisRepresentations_105106580_-5.gif) be a closed point. Then we know from the above bijection and the universal property that
be a closed point. Then we know from the above bijection and the universal property that  corresponds to a representation
corresponds to a representation 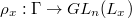 . Let
. Let 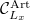 to be the category of local Artinian
to be the category of local Artinian 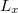 -algebra with residue field
-algebra with residue field 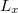 .
.
![$\Hom(R^\Box[1/\ell]_x^\wedge,A)=\mathcal{R}^\Box_{\rho_x}(A)$](./latex/latex2png-GaloisRepresentations_156798025_-6.gif) , functorial in
, functorial in 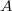 . Though
. Though 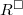 is constructed as the deformations of a representation in characteristic
is constructed as the deformations of a representation in characteristic  , the generic fiber of
, the generic fiber of 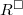 knows about deformations of representations in characteristic 0.
knows about deformations of representations in characteristic 0.
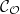 (so the functor is in fact representable in
(so the functor is in fact representable in 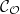 ). But Artinian rings are easier to deal with because the topology on finite dimensional representations are obvious (the
). But Artinian rings are easier to deal with because the topology on finite dimensional representations are obvious (the  -adic topology).
-adic topology).
![$f: R^\Box[1/\ell]_x^\wedge\rightarrow A$](./latex/latex2png-GaloisRepresentations_70557663_-5.gif) , one simply composes to get
, one simply composes to get ![$R^\Box\rightarrow GL_n(R^\Box)\rightarrow GL_n(R^\Box[1/\ell]_x^\wedge)\xrightarrow{f}GL_n(A)$](./latex/latex2png-GaloisRepresentations_264406199_-5.gif) , an object in
, an object in 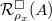 .
.
Conversely, given 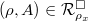 , let
, let 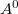 be the
be the 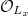 -subalgebra of
-subalgebra of 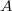 generated by the entries
generated by the entries 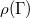 . One can show by a compactness argument that
. One can show by a compactness argument that 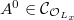 and is finitely generated as
and is finitely generated as 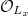 -module. Let
-module. Let 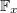 be the residue field of
be the residue field of 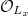 . Reducing
. Reducing  then gives
then gives 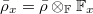 . One can show (homework) that
. One can show (homework) that 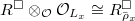 , so the universal property gives the map
, so the universal property gives the map 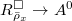 , hence a map
, hence a map 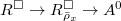 . By the universal property of localization, it extends to a map on the generic fiber
. By the universal property of localization, it extends to a map on the generic fiber ![$R^\Box[1/\ell]\rightarrow A^0[1/ \ell]$](./latex/latex2png-GaloisRepresentations_112869971_-5.gif) . By continuity, it extends to the completion
. By continuity, it extends to the completion ![$R^\Box[1/\ell]_x^\wedge\rightarrow A$](./latex/latex2png-GaloisRepresentations_70721915_-5.gif) . For more details, see Brian's notes at Stanford seminar on modularity liftings.
¡õ
. For more details, see Brian's notes at Stanford seminar on modularity liftings.
¡õ
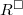 .
.
 Deformation problems
Deformation problems
In practice, we are more interested in lifting Galois representations with prescribed local behaviors (e.g., requiring good reduction at certain primes for elliptic curves). So one would like to work with certain subspaces of 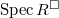 (or in terms of rings, certain quotient rings of
(or in terms of rings, certain quotient rings of 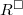 ). We would like to make a checklist for technical conditions to define nice subspaces of
). We would like to make a checklist for technical conditions to define nice subspaces of 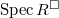 .
.
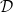 is a collection
is a collection 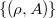 , where
, where 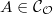 ,
, 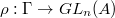 is a lifting of
is a lifting of 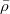 such that
such that
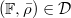 .
.- If
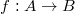 is a map in
is a map in 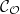 and
and 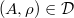 , then
, then 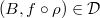 .
. - (restriction) If
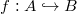 and
and 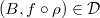 , then
, then 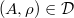 .
. - (gluing) Let
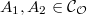 with ideals
with ideals 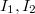 and
and 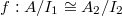 . Suppose
. Suppose 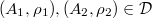 such that
such that 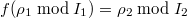 , then
, then 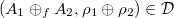 . Here
. Here 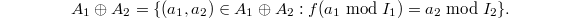
- (nested intersection) Suppose
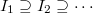 is a chain of ideals of
is a chain of ideals of 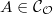 such that
such that 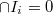 . Suppose
. Suppose 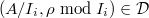 , then
, then 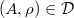 .
. - (conjugate) If
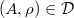 ,
, 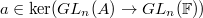 , then
, then 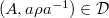 .
.
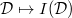 is characterized by
is characterized by 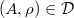 if and only if
if and only if 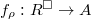 is trivial on
is trivial on 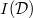 . Conversely, when
. Conversely, when 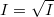 and
and 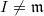 (these restrictions are needed to check f), for this subtlety, see [BLGHT] Lem 3.2), we have
(these restrictions are needed to check f), for this subtlety, see [BLGHT] Lem 3.2), we have 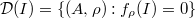 .
.
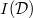 is uniquely determined. Let
is uniquely determined. Let 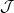 be the set of all ideals
be the set of all ideals 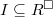 such that
such that 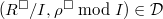 . This is nonempty by a). Using b) and c), we know
. This is nonempty by a). Using b) and c), we know 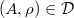 if and only if
if and only if  . Moreover
. Moreover 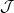 is closed under finite intersection and nested infinite intersection by d) and e). So by Zorn's lemma, there exists a unique minimal ideal
is closed under finite intersection and nested infinite intersection by d) and e). So by Zorn's lemma, there exists a unique minimal ideal 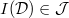 . It is kernel invariant by f).
¡õ
. It is kernel invariant by f).
¡õ
03/11/2014
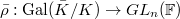 , where
, where 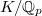 is a local field. See [CHT] 2.4 for several examples: when
is a local field. See [CHT] 2.4 for several examples: when 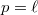 , the Fontaine-Laffaille liftings or ordinary liftings; when
, the Fontaine-Laffaille liftings or ordinary liftings; when 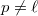 , Taylor-Wiles liftings, are all deformation problems.
, Taylor-Wiles liftings, are all deformation problems.
For applications, it is important to understand the ring theoretic properties of 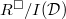 , e.g., Krull dimension, number of generators, number of relations and so on. We computed these for
, e.g., Krull dimension, number of generators, number of relations and so on. We computed these for 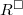 in terms of Galois cohomology. It is similar for
in terms of Galois cohomology. It is similar for 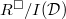 .
.
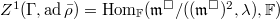 , one can consider the annihilator of the image of
, one can consider the annihilator of the image of 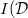 in
in 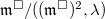 ,
, 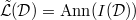 (think: the subspace cut out by
(think: the subspace cut out by 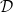 of the tangent space). We define
of the tangent space). We define 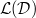 be its image in
be its image in 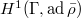 .
.
Using the kernel-invariance property of 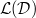 , one can show that
, one can show that
So one can work directly at the level of cohomology instead of cocycles.
 Global Galois deformation problems
Global Galois deformation problems
We begin with a remark on fixing the determinant.
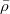 to
to 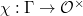 such that
such that 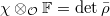 , then one obtains a subfunctor
, then one obtains a subfunctor 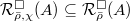 by requiring the extra condition
by requiring the extra condition 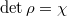 on the liftings (
on the liftings (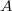 is an
is an 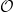 -algebra, so this makes sense). This subfunctor
-algebra, so this makes sense). This subfunctor 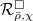 is represented by a ring
is represented by a ring 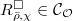 (one can construct
(one can construct 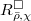 as the quotient of
as the quotient of 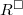 by the equation
by the equation 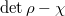 ). The previous discussion all carries over to this setting: the main change is that
). The previous discussion all carries over to this setting: the main change is that 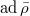 should be replaced by
should be replaced by 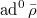 (the traceless subspace).
(the traceless subspace).
Now let 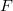 be a number field. Let
be a number field. Let  be a place of
be a place of 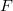 and fix
and fix 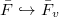 . One has the local Galois group
. One has the local Galois group 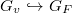 (well-defined up to conjugation). Let
(well-defined up to conjugation). Let 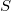 be a set of finite places of
be a set of finite places of 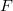 and
and 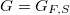 .
.
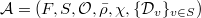 , where
, where
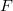 ,
, 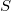 ,
, 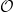 as above;
as above;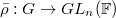 is absolutely irreducible (the work of Skinner-Wiles and Thorne can relax this condition);
is absolutely irreducible (the work of Skinner-Wiles and Thorne can relax this condition);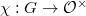 such that
such that 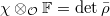 ;
;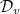 is a deformation problem for
is a deformation problem for 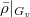 .
.
Next we will define a deformation functor and show it is representable and study its ring theoretic properties.
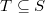 (may be empty). Define the functor
(may be empty). Define the functor 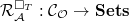 given by
given by 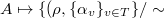 . Here
. Here
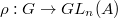 is a lifting of
is a lifting of 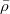 with
with 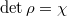 ,
,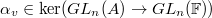 ,
,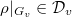 for
for 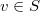 .
.
The equivalence relations 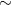 is generated by the following: for any
is generated by the following: for any 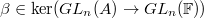 ,
, 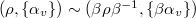 .(Think: we are imposing local conditions at
.(Think: we are imposing local conditions at  and "framing at
and "framing at  "; this helps the Galois cohomology calculation and also helps achieving the final goal of comparing the deformation ring with the Hecke ring).
"; this helps the Galois cohomology calculation and also helps achieving the final goal of comparing the deformation ring with the Hecke ring).
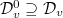 be all liftings of
be all liftings of 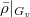 and
and 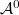 be the deformation problem given by
be the deformation problem given by 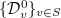 . Then
. Then 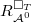 is representable (which is
is representable (which is  if
if 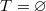 ). Then one can construct
). Then one can construct 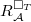 as
as 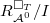 , where
, where 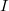 is the minimal ideal such that
is the minimal ideal such that  factors through
factors through 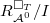 if and only if
if and only if 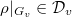 for
for 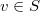 . For more details, see [CHT].
¡õ
. For more details, see [CHT].
¡õ
 Presenting global deformation rings over local lifting rings
Presenting global deformation rings over local lifting rings
We have seen how to represent 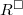 over
over 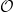 and when
and when 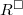 happens to be a power series ring over
happens to be a power series ring over 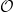 . We are now going to represent
. We are now going to represent 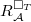 over another bigger ring, the local lifting ring. This idea is due to Kisin.
over another bigger ring, the local lifting ring. This idea is due to Kisin.
Notice 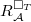 has the following universal object:
has the following universal object:
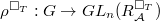 , and
, and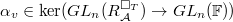 ,
, 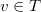 .
.
By the kernel-invariance property, 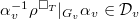 . Moreover, it is well-defined element independent of the choice of the representative of the equivalence class. By the universal property of
. Moreover, it is well-defined element independent of the choice of the representative of the equivalence class. By the universal property of 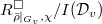 , we know that
, we know that 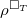 factors through
factors through 
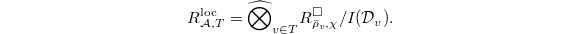 We have a natural map
We have a natural map 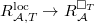 .
.
Our next goal is to find the number of the generators and relations for presenting 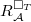 over
over 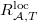 using Galois cohomology.
using Galois cohomology.
As a first thought, suppose 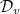 consists of all liftings. Write
consists of all liftings. Write 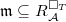 and
and 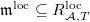 be the maximal ideals. The the same argument as in Lemma 6 shows that
be the maximal ideals. The the same argument as in Lemma 6 shows that ![$$\Hom_\mathbb{F}(\mathfrak{m}/(\mathfrak{m}^2,\lambda),\mathbb{F})=\mathcal{R}_\mathcal{A}^{\Box_T}(\mathbb{F}[\varepsilon]/(\varepsilon^2))\cong \frac{Z^1(G,\ad^0\bar\rho)\oplus\bigoplus_{v\in T}1+\varepsilon M_n(\mathbb{F})}{1+\varepsilon M_n(\mathbb{F})}.$$](./latex/latex2png-GaloisRepresentations_97762865_.gif) Here
Here 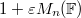 sits diagonally. Rewriting this as
sits diagonally. Rewriting this as 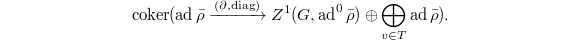
Two modifications are needed in general:
- to consider the tangent space over
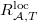 : one should replace
: one should replace 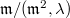 by
by 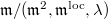 . Concretely, this requires the liftings at
. Concretely, this requires the liftings at 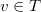 to be trivial, i.e.,
to be trivial, i.e.,  lies in the kernel of
lies in the kernel of 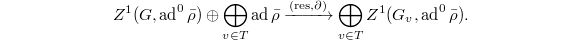 Notice the image of
Notice the image of 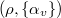 is
is 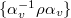 , which we require to be trivial, i.e.,
, which we require to be trivial, i.e., 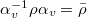 . Write
. Write 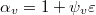 and
and 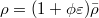 , then
, then 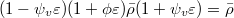 if and only if
if and only if 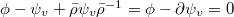 .
. - to allow general
 for
for  : one requires that
: one requires that 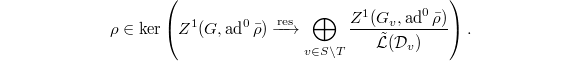
The upshot is that 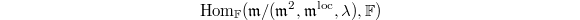 is the
is the 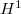 of the complex
of the complex 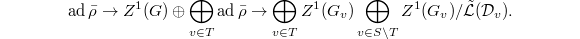
This motivates the definition of the mysterious complex in [Gee].
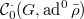 to be the complex in the first row and
to be the complex in the first row and  to be complex in the second row. So
to be complex in the second row. So 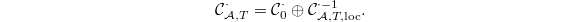
We define 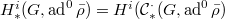 , for
, for 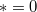 or
or 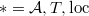 .
.
Next time we shall study the cohomology 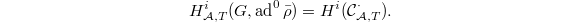 Similarly, the number of generators will be given by
Similarly, the number of generators will be given by 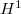 and the number of generators will be bounded by
and the number of generators will be bounded by 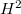 . Can we compute
. Can we compute  and
and 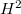 ? This needs serious input from Galois cohomology, which we will do next time.
? This needs serious input from Galois cohomology, which we will do next time.
03/13/2014
Our next goal is to compute 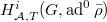 for
for 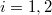 in terms of
in terms of
- the usual local and global Galois cohomology,
- the dimension of the local conditions
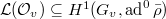 ,
, - the dimension of the "dual Selmer group" (as the error term).
 Computation of
Computation of 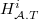
Assume for simplicity that
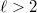 (
(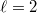 causes, e.g., problems at real places; see Kisin's modularity results on 2-adic representations),
causes, e.g., problems at real places; see Kisin's modularity results on 2-adic representations),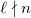 . This implies that there exists a splitting of Galois modules
. This implies that there exists a splitting of Galois modules 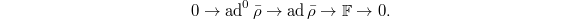
- all places above of
 above
above  lies in
lies in  (this is a harmless assumption).
(this is a harmless assumption).
The fact is that all cohomology groups are finite dimensional over  and concentrate in bounded degree. So we can define the Euler characteristic
and concentrate in bounded degree. So we can define the Euler characteristic 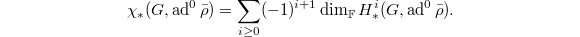
There are four steps to compute  .
.
Step 1
We have
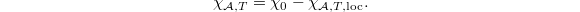 This is clear exact sequence of complexes
This is clear exact sequence of complexes 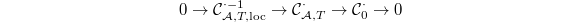 and the fact that the Euler characteristic is additive in long exact sequences. It follows that
and the fact that the Euler characteristic is additive in long exact sequences. It follows that 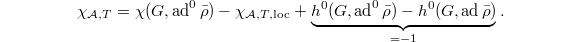 The latter is equal to
The latter is equal to 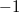 due to the existence of the splitting
due to the existence of the splitting 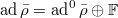 .
.
Step 2
We compute  in terms of usual Galois cohomology. By definition,
in terms of usual Galois cohomology. By definition, 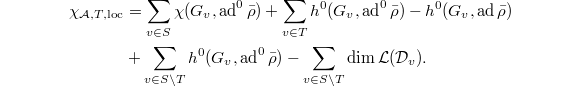 Again, the second term is equal to
Again, the second term is equal to 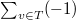 . Therefore
. Therefore 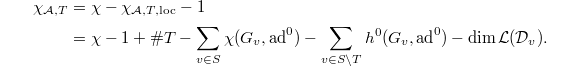
Step 3
Apply the local and global Euler-Poincare characteristic formula to 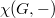 and
and 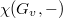 to get a formula for
to get a formula for 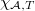 .
.
Step 4
It turns out  when
when 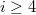 .
. 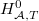 is always easy. By the Euler-Poincare characteristic, to compute
is always easy. By the Euler-Poincare characteristic, to compute 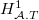 , it remains to compute
, it remains to compute 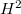 and
and 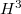 . The Poitou-Tate duality allows one to understand
. The Poitou-Tate duality allows one to understand 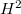 and
and 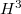 in terms of
in terms of 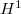 (this is the error term mentioned above) and
(this is the error term mentioned above) and 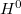 (easy) of the dual Galois module. When the error term vanishes,
(easy) of the dual Galois module. When the error term vanishes, 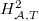 is zero so the deformation ring is indeed a power series ring.
is zero so the deformation ring is indeed a power series ring.
To execute the last two steps, We need the following facts.
- Let
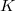 be a nonarchimedean local field and
be a nonarchimedean local field and 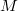 be a finite
be a finite ![$\mathbb{F}[G_K]$](./latex/latex2png-GaloisRepresentations_135163825_-5.gif) -module. Then
-module. Then 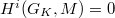 for
for 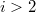 . (
. (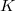 has cohomological dimension 2).
has cohomological dimension 2). - When
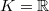 ,
,  for
for 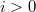 (here we use the assumption that
(here we use the assumption that 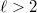 ).
). - When
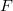 is a number field and
is a number field and 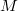 is a finite
is a finite ![$\mathbb{F}[G=G_{F,S}]$](./latex/latex2png-GaloisRepresentations_161142105_-5.gif) -module,
-module, 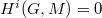 for
for 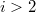 (here we use the assumption that
(here we use the assumption that 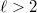 as well: the
as well: the  -cohomological dimension of a number field is 2 when
-cohomological dimension of a number field is 2 when 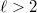 ).
).
From the long exact sequence in cohomology, it follows that
Another input is the determination of the Euler-Poincare characteristics.
- When
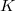 is a nonarchimedean local field of characteristic 0, then
is a nonarchimedean local field of characteristic 0, then 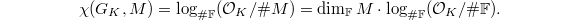 This is zero unless
This is zero unless 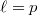 , in which case is
, in which case is ![$\dim_\mathbb{F}M\cdot [K: \mathbb{Q}_p=\mathbb{Q}_\ell]$](./latex/latex2png-GaloisRepresentations_59008094_-5.gif) .
. - When
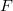 is a number field and
is a number field and 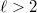 , then
, then ![$$\chi(G_{F,S},M)=[F: \mathbb{Q}]\dim_\mathbb{F}M-\sum_{v\mid \infty}h^0(G_v,M).$$](./latex/latex2png-GaloisRepresentations_58262687_.gif)
The final key inputs are the local and global duality theorems.
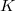 be a local or global field. Let
be a local or global field. Let 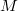 be a finite
be a finite ![$\mathbb{F}[G_K]$](./latex/latex2png-GaloisRepresentations_135163825_-5.gif) -module. Let
-module. Let 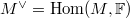 be the linear dual and
be the linear dual and 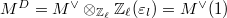 be the Cartier dual. Here
be the Cartier dual. Here 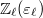 the twist of
the twist of 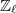 by the cyclotomic character
by the cyclotomic character 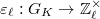 .
.
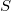 is infinite,
is infinite, 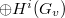 needs to be replaced with the restricted product with respect to the unramified parts, which is the direct product (direct sum) when
needs to be replaced with the restricted product with respect to the unramified parts, which is the direct product (direct sum) when 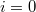 (
(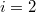 ), since
), since 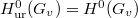 (
(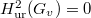 ); When
); When 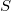 contains infinite places, the corresponding
contains infinite places, the corresponding 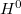 should be replaced by
should be replaced by 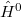 .
.
Back to our situation with 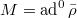 , by definition we have the following exact sequence
, by definition we have the following exact sequence
![$$\xymatrix{ & H^1(G,M) \ar[r] & \displaystyle\bigoplus_{v\in T}H^1(G_v,M)\bigoplus_{v\in S\setminus T}H^1(G_v,M)/\mathcal{L}(\mathcal{D}_v) \ar[r] & H^2_{\mathcal{A},T} \\ \ar[r] & H^2(G,M) \ar[r] & \displaystyle\bigoplus_{v\in S}H^2(G_v,M) \ar[r] & H^3_{\mathcal{A},T}.}$$](./latex/latex2png-GaloisRepresentations_186561407_.gif)
Notice that 1, 4, 5 terms are the same as in Poitou-Tate.
Suppose we have a commutative diagram
![$$\xymatrix{1 \ar[r] \ar[d]^{=}& 2 \ar[r]^{\gamma} \ar[d]& 3 \ar[r] \ar[d] & 4 \ar[d]^{=}\\ 1 \ar[r] & 2/N \ar[r] & 3/\gamma(N) \ar[r] & 4}.$$](./latex/latex2png-GaloisRepresentations_87544349_.gif) where
where 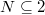 is a subspace. If the top row is exact, then the second row is still exact. Take the first row to be the Poitou-Tate exact sequence and
is a subspace. If the top row is exact, then the second row is still exact. Take the first row to be the Poitou-Tate exact sequence and 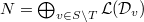 . Then
. Then

It follows that 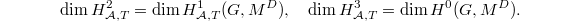 Since
Since 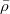 is absolutely irreducible, we also know that
is absolutely irreducible, we also know that 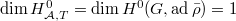 . Combining these with the Euler-Poincare characteristics computation, we obtain desired formulas for
. Combining these with the Euler-Poincare characteristics computation, we obtain desired formulas for 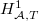 and
and 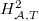 . For explicit expressions, see [Gee] 3.24.
. For explicit expressions, see [Gee] 3.24.
03/18/2014
(I was out of town for AWS 2014, this section is shameless copied from Rong Zhou's typed notes.)
The notation is as above. 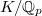 is a finite extension and
is a finite extension and 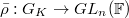 is a continuous representations, and fix a character
is a continuous representations, and fix a character 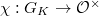 , which reduces to
, which reduces to 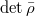 .
.
We constructed the ring 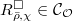 which represents the lifting problem for
which represents the lifting problem for 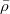 with the fixed determinant
with the fixed determinant 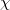 . Its generic fiber
. Its generic fiber ![$R^\Box_{\bar\rho,\chi}[1/\ell]$](./latex/latex2png-GaloisRepresentations_203483901_-6.gif) has closed points corresponding to
has closed points corresponding to  -adic liftings of
-adic liftings of 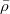 with determinant
with determinant 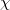 .
.
The goal of the next week will be to study the properties (e.g. irreducible components, dimension) of ![$R^\Box_{\bar\rho,\chi}[1/\ell]$](./latex/latex2png-GaloisRepresentations_203483901_-6.gif) (or
(or 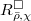 ). We split into the two cases
). We split into the two cases 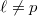 and
and 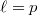 (the second requires some background in
(the second requires some background in 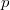 -adic hodge theory). This information (irreducible components, dimension) enters into the proof of automorphy lifting theorems. In order to control
-adic hodge theory). This information (irreducible components, dimension) enters into the proof of automorphy lifting theorems. In order to control 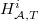 (
(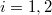 ) or the Krull dimension of
) or the Krull dimension of 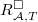 , we saw last time that we need to know the
, we saw last time that we need to know the 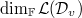 , or the Krull dimension of
, or the Krull dimension of 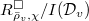 .
.
 Local universal lifting rings
Local universal lifting rings 
![$\Spec R^\Box_{\bar\rho,\chi}[1/\ell]$](./latex/latex2png-GaloisRepresentations_195019054_-6.gif) has finitely many irreducible components and each irreducible component is generically formally smooth (over
has finitely many irreducible components and each irreducible component is generically formally smooth (over 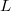 ) and of dimension
) and of dimension 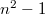 .
.
 of
of ![$\Spec R^\Box[1/\ell]$](./latex/latex2png-GaloisRepresentations_148492784_-5.gif) corresponding to the
corresponding to the  -adic representation
-adic representation 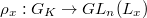 to be smooth if
to be smooth if 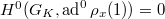 . It is shown in [BLGGT], Lemma 1.3.2 that the smooth points are Zariski dense. Thus it suffices to prove that
. It is shown in [BLGGT], Lemma 1.3.2 that the smooth points are Zariski dense. Thus it suffices to prove that ![$R^\Box[1/\ell]^\wedge_x\cong L_x[ [y_1,...,y_{n^2-1}] ]$](./latex/latex2png-GaloisRepresentations_182851690_-5.gif) . Notice this ring is the universal lifting ring for
. Notice this ring is the universal lifting ring for 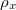 with coefficients in
with coefficients in 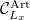 (Lemma 9). The idea is to mimic the argument for liftings of
(Lemma 9). The idea is to mimic the argument for liftings of 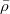 using tangent spaces and Galois cohomology. Define
using tangent spaces and Galois cohomology. Define 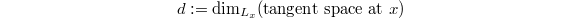 which, if we fix the determinant, is equal to
which, if we fix the determinant, is equal to  Hence there exists a surjection
Hence there exists a surjection ![$$\phi:L_x[ [x_1,...,x_d] ]\twoheadrightarrow R^\Box[1/\ell]_x^\wedge.$$](./latex/latex2png-GaloisRepresentations_259215030_.gif) One shows in the same way as before that
One shows in the same way as before that 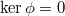 if
if 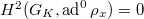 .
.
Thus it suffices to prove 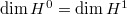 and
and 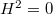 . This follows from the
. This follows from the  -adic version of local duality and the Euler-Poincare formula. The first gives us
-adic version of local duality and the Euler-Poincare formula. The first gives us 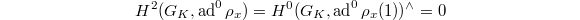 (the second equality follows from the smoothness), and the second gives
(the second equality follows from the smoothness), and the second gives 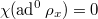 . These two together imply what we wanted.
¡õ
. These two together imply what we wanted.
¡õ
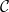 be a nonempty subset of irreducible components of
be a nonempty subset of irreducible components of ![$\Spec R^\Box[1/\ell]$](./latex/latex2png-GaloisRepresentations_148492784_-5.gif) . We define
. We define 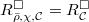 to be the largest quotient of
to be the largest quotient of 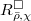 which is
which is
- reduced and
 -torsion free;
-torsion free; ![$\Spec R^\Box_{\bar\rho,\chi,\mathcal{C}}[1/\ell]\subset \mathcal{C}$](./latex/latex2png-GaloisRepresentations_92899507_-7.gif) .
.
![$$\overline{R}^\Box:=R^\Box/\ell\text{-torsion}\hookrightarrow R^\Box[1/\ell].$$](./latex/latex2png-GaloisRepresentations_102759545_.gif) Then
Then ![$\Spec R^\Box[1/\ell]\subset \Spec \overline{R}^\Box$](./latex/latex2png-GaloisRepresentations_207010817_-5.gif) is open dense. Take the closure
is open dense. Take the closure 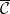 of
of 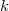 in
in 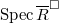 and then take the reduced closed subscheme structure on
and then take the reduced closed subscheme structure on 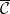 .
.
- The non-trivial part is to show that
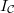 is
is 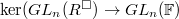 invariant (this is [BLGGT] Lemma 1.2.2).
invariant (this is [BLGGT] Lemma 1.2.2). ![$\Spec R^\Box[1/\ell]$](./latex/latex2png-GaloisRepresentations_148492784_-5.gif) is open and dense in
is open and dense in 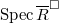 . Let
. Let 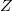 be an irreducible component of
be an irreducible component of 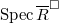 and define
and define ![$Z':=Z\cap\Spec R^\Box[1/\ell]$](./latex/latex2png-GaloisRepresentations_89534304_-5.gif) . One checks that
. One checks that 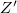 is an irreducible component and is non-empty with
is an irreducible component and is non-empty with 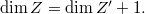 In fact, suppose
In fact, suppose 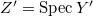 and
and 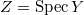 . Take a sequence of ideals:
. Take a sequence of ideals: 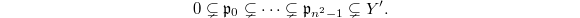 Then
Then 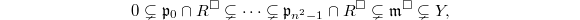 since the quotient
since the quotient 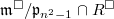 is the ring of integers in a finite extension of
is the ring of integers in a finite extension of 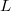 .
¡õ
.
¡õ
Now consider the map which takes finite dimensional Weil-Deligne representations of 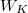 on
on 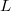 -vector space to equivalence classes of triples
-vector space to equivalence classes of triples 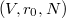 , where
, where 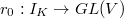 is an representation of the inertia subgroup,
is an representation of the inertia subgroup, 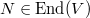 is nilpotent, and
is nilpotent, and  and
and  commute.
commute.
 in the image. A Weil-Deligne representation is of type
in the image. A Weil-Deligne representation is of type  if it lies in the preimage of
if it lies in the preimage of  .
.
 (or
(or 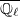 ) coefficients, there are four inertial types:
) coefficients, there are four inertial types:
- Unramified up to character
![$\tau=[(\psi\oplus\psi,0)]$](./latex/latex2png-GaloisRepresentations_54626780_-5.gif) ,
, 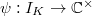 a character.
a character. - Steinberg:
![$\tau=[(\psi\oplus\psi, \left(\begin{smallmatrix} 0& 1 \\ 0 & 0\end{smallmatrix}\right)]$](./latex/latex2png-GaloisRepresentations_211423577_-5.gif) .
. - Split unramified:
![$\tau=[(\psi_1\oplus\psi_2,0)]$](./latex/latex2png-GaloisRepresentations_154556334_-5.gif) where
where 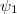 and
and 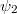 are two distinct characters of
are two distinct characters of 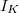 .
. - Irreducible type:
![$\tau=[(r_0,0)]$](./latex/latex2png-GaloisRepresentations_199397820_-5.gif) comes from an irreducible Weil-Deligne representations of dimension 2.
comes from an irreducible Weil-Deligne representations of dimension 2.
Notice that an irreducible Weil-Deligne representation may restrict to a reducible representation of 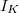 . To make type c) and d) disjoint, we make the additional condition that type c) comes reducible Weil-Deligne representations.
. To make type c) and d) disjoint, we make the additional condition that type c) comes reducible Weil-Deligne representations.
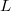 is sufficiently large (or we can work with geometrical irreducible components). Then
is sufficiently large (or we can work with geometrical irreducible components). Then
- Each irreducible component
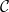 of
of ![$\Spec R^\Box[1/\ell]$](./latex/latex2png-GaloisRepresentations_148492784_-5.gif) has associated type
has associated type 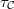 such that:
such that:
- Closed points corresponds to
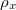 such that
such that 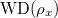 has type
has type 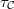 (type a), c), d)), or
(type a), c), d)), or - Closed points correspond to
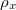 fitting into an exact sequence
fitting into an exact sequence 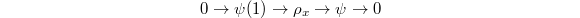 for some
for some  (type a) or b)).
(type a) or b)).
- Closed points corresponds to
- Each type occurs in at most one component with the following exception: if
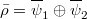 with
with 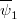 and
and 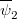 distinct, and
distinct, and 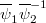 is unramified, then there exists 2 components with type c).
is unramified, then there exists 2 components with type c). - Two components intersect only when the two components are of type a) and type b), the representations in the component corresponding to type a) are of the form
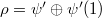 and those of type b) are of the form
and those of type b) are of the form 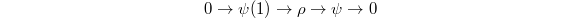 such that
such that 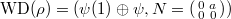 . As one approaches the intersection point,
. As one approaches the intersection point,  approaches
approaches 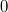 and
and 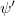 approaches
approaches 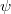 , the representation at the intersection point is
, the representation at the intersection point is 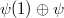 .
. - Each component is formally smooth.
 is the intersection point, the proof of the previous proposition implies that
is the intersection point, the proof of the previous proposition implies that 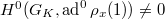 . Hence
. Hence ![$$0\neq \ad\rho_x(1)^{G_K}=\Hom_{L_x}(\rho_x,\rho_x(1))^{G_K}=\Hom_{L_x[G_K]}(\rho_x,\rho_x(1)).$$](./latex/latex2png-GaloisRepresentations_239263999_.gif) This implies
This implies 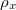 is reducible
is reducible 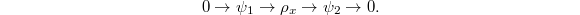 Hence
Hence 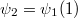 and
and 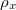 is split, i.e..
is split, i.e.. 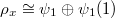 .
.
03/20/2014
Last time we looked at local universal lifting rings for 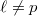 . We will leave the important Taylor-Wiles deformation (allowing auxiliary primes with ramification) in the homework. Another important deformation problem is the Ihara avoidance defomations due to Taylor (for
. We will leave the important Taylor-Wiles deformation (allowing auxiliary primes with ramification) in the homework. Another important deformation problem is the Ihara avoidance defomations due to Taylor (for 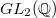 , Ihara's lemma allows one to raise the level; but Ihara's lemma is not known in higher dimensional. The Ihara avoidance deformation was introduced to bypass Ihara's lemma).
, Ihara's lemma allows one to raise the level; but Ihara's lemma is not known in higher dimensional. The Ihara avoidance deformation was introduced to bypass Ihara's lemma).
 Local universal lifting rings
Local universal lifting rings 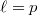
As always, all Galois representations are finite dimensional on 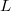 -vector spaces. There are more
-vector spaces. There are more 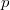 -adic representations of
-adic representations of 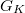 than
than  -adic representations
-adic representations 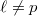 (where the wild inertia is almost killed). The slogan of
(where the wild inertia is almost killed). The slogan of 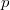 -adic Hodge theory is to try to understand
-adic Hodge theory is to try to understand 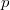 -adic representations of
-adic representations of 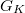 through linear algebraic categories via equivalence (at least fully faithful embeddings) of categories. There exists a hierarchy of
through linear algebraic categories via equivalence (at least fully faithful embeddings) of categories. There exists a hierarchy of 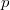 -adic Galois representations:
-adic Galois representations:
crystalline 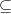 semistable
semistable  potentially semistable ( = de Rham)
potentially semistable ( = de Rham)  Hodge-Tate
Hodge-Tate  all
all
We will not explain these technical terms but show some analogies with  -adic (
-adic ( ) representations and representations comes from geometry (smooth projective varieties
) representations and representations comes from geometry (smooth projective varieties 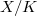 ).
).
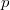 -adic -adic |
crystalline | semistable | potentially semistable | de Rham |
 -adic -adic |
unramified | inertia acting unipotently | inertia acting potentially unipotent | all |
smooth projective variety 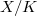 |
good reduction | semistable reduction | potentially semistable reduction | all |
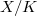 with good reduction gives rises to unramified
with good reduction gives rises to unramified  -adic representations (but the converse is not true). It is still a conjecture that all smooth projective varieties are potentially semistable. Notice by Grothendieck's
-adic representations (but the converse is not true). It is still a conjecture that all smooth projective varieties are potentially semistable. Notice by Grothendieck's  -adic monodromy theorem, all
-adic monodromy theorem, all  -adic representations are potentially unipotent.
-adic representations are potentially unipotent.
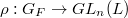 comes from automorphic forms, then
comes from automorphic forms, then 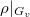 (for
(for 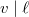 ) is potentially semistable (=de Rham). Conversely, if
) is potentially semistable (=de Rham). Conversely, if  is potentially semistable at
is potentially semistable at 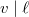 and unramified at almost all places, then
and unramified at almost all places, then  should be automorphic. From this philosophy it is natural to impose potentially semistable condition at
should be automorphic. From this philosophy it is natural to impose potentially semistable condition at 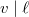 so that
so that 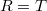 theorem has a chance to be true.
theorem has a chance to be true.
There are two important invariants associated to potentially semistable representations: WD (a Weil-Deligne representation of 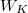 ) and HT (Hodge-Tate weights, a multiset of integers).
) and HT (Hodge-Tate weights, a multiset of integers).
 The Weil-Deligne functor
The Weil-Deligne functor
When 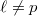 , taking the Weil-Deligne representation gives a functor from all
, taking the Weil-Deligne representation gives a functor from all 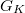 -representations to WD-representations of
-representations to WD-representations of 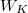 . When
. When 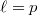 , we only define the Weil-Deligne representation functor for potentially semistable representations. Let
, we only define the Weil-Deligne representation functor for potentially semistable representations. Let 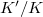 be a finite Galois extension and
be a finite Galois extension and 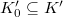 be the maximal unramified subextension over
be the maximal unramified subextension over 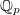 . Take
. Take 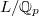 to be sufficient large (containing the Galois closure of
to be sufficient large (containing the Galois closure of 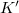 ), e.g.,
), e.g., 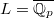 . Let
. Let 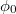 be the absolute Frobenius on
be the absolute Frobenius on 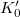 .
.
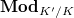 to be the category of
to be the category of 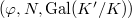 -modules
-modules  . Here
. Here
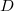 is a finite rank free
is a finite rank free 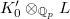 -module;
-module;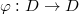 is a bijection and
is a bijection and 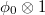 -semilinear, i.e.,
-semilinear, i.e., 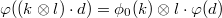 ;
;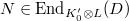 is nilpotent and
is nilpotent and 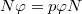 ;
;- The
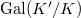 -action on
-action on 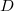 is semilinear and commutes with
is semilinear and commutes with 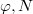 .
.
- There exists a dimension preserving functor
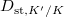 from the category of potentially semistable representations
from the category of potentially semistable representations  such that
such that 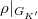 is semistable to the category
is semistable to the category 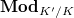 .
. - There exists an equivalence between
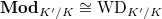 .
.
We treat the first functor as a black box (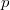 -adic Hodge-Tate theorem). The second functor is purely linear algebraic and can be described more easily. Let
-adic Hodge-Tate theorem). The second functor is purely linear algebraic and can be described more easily. Let 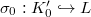 be an embedding. Suppose
be an embedding. Suppose 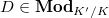 , we define
, we define 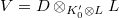 via
via 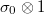 and
and 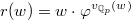 , here
, here 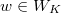 ,
, 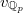 is the absolute
is the absolute 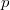 -adic valuation, and
-adic valuation, and 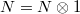 . Then
. Then 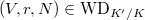 and the isomorphism class does not depend on
and the isomorphism class does not depend on 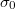 .
.
Allowing 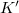 to be larger and larger, we obtain a functor from potentially semistable
to be larger and larger, we obtain a functor from potentially semistable 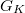 -representations to the category of WD-representations of
-representations to the category of WD-representations of 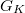 (
(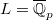 ).
).
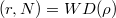 . Then
. Then  is semistable if and only if
is semistable if and only if  is unramified;
is unramified;  is crystalline if and only if
is crystalline if and only if  is unramified and
is unramified and 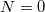 ;
;  is potentially crystalline if and only if
is potentially crystalline if and only if 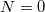 . Moreover,
. Moreover, 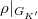 is semistable if and only if
is semistable if and only if 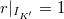 and
and 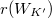 centralizes
centralizes 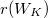 .
.
 Hodge-Tate weights
Hodge-Tate weights
Given 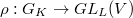 , we will define a collection
, we will define a collection 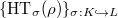 , where
, where 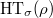 is an unordered multiset of integers. Each
is an unordered multiset of integers. Each 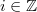 in
in 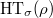 has the following multiplicity
has the following multiplicity 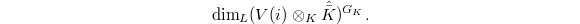 It is known that the sum of all these multiplicities is equal to
It is known that the sum of all these multiplicities is equal to 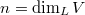 (for any Hodge-Tate representation). These numbers can be read off from some natural filtration (defined after extending coefficients) attached to
(for any Hodge-Tate representation). These numbers can be read off from some natural filtration (defined after extending coefficients) attached to  .
.
 is an abelian variety and
is an abelian variety and  is given by its
is given by its 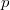 -adic Tate module. Then
-adic Tate module. Then 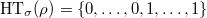 with 0 and 1 each occurring
with 0 and 1 each occurring 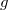 times.
times.
 from
from 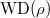 and
and 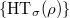 uniquely? This is the case when the latter data has an "admissible filtration". Breuil-Scheider conjectured a nice answer to what these should correspond to on the
uniquely? This is the case when the latter data has an "admissible filtration". Breuil-Scheider conjectured a nice answer to what these should correspond to on the 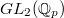 -side, which is part of the beginning of the
-side, which is part of the beginning of the 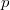 -adic Langlands program.
-adic Langlands program.
 Potentially semistable local lifting rings
Potentially semistable local lifting rings
 , where each
, where each 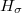 consists of distinct integers.
consists of distinct integers.
- There exists a unique
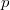 -torsion-free, reduced quotient
-torsion-free, reduced quotient 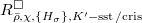 of
of 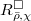 such that for any closed (geometric) point
such that for any closed (geometric) point  of
of ![$R^{\Box}_{\bar\rho,\chi}[1/p]$](./latex/latex2png-GaloisRepresentations_247694321_-6.gif) ,
,  factors through this quotient if and only if
factors through this quotient if and only if 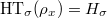 and
and 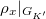 is semistable/crystalline.
is semistable/crystalline. 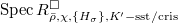 is equidimensional of dimension
is equidimensional of dimension ![$n^2+[K:\mathbb{Q}_p]n(n-1)/2$](./latex/latex2png-GaloisRepresentations_10821806_-5.gif) . Its generic fiber is generically smooth.
. Its generic fiber is generically smooth.
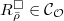 .
.
![$\End_{k[\Gamma]}(\rho)=\{\phi\in\End_k(V): \phi\rho(\gamma)=\rho(\gamma)\phi,\forall \gamma\in\Gamma\}$](./latex/latex2png-GaloisRepresentations_260279013_-6.gif) is a division algebra over
is a division algebra over  is algebraically closed. Let
is algebraically closed. Let 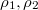 be irreducible representations. Then
be irreducible representations. Then ![$$\Hom_{k[\Gamma]}(\rho_1,\rho_2)=
\begin{cases}
k & \rho_1\cong\rho_2,\\
0 & \rho_1\not\cong\rho_2.
\end{cases}$$](./latex/latex2png-GaloisRepresentations_69992204_.gif)
![$k[\Gamma]\rightarrow \End_k(V)$](./latex/latex2png-GaloisRepresentations_251315174_-5.gif) is surjective.
is surjective.
 is representable. Say by
is representable. Say by 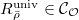 , the universal deformation ring of
, the universal deformation ring of 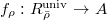 such that
such that 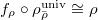 .
.
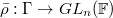 is absolutely irreducible. If
is absolutely irreducible. If 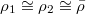 such that
such that 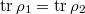 . Then
. Then 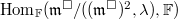 .
.![$\Hom_{\mathcal{C}_\mathcal{O}}(R^\Box,\mathbb{F}[\varepsilon]/\varepsilon^2)$](./latex/latex2png-GaloisRepresentations_91497733_-5.gif) .
.![$\mathcal{R}^\Box(\mathbb{F}[\varepsilon]/\varepsilon^2)$](./latex/latex2png-GaloisRepresentations_232566604_-5.gif) (liftings of
(liftings of ![$\mathbb{F}[\varepsilon]/\varepsilon^2$](./latex/latex2png-GaloisRepresentations_244827125_-5.gif) ).
).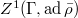 (continuous 1-cocycles).
(continuous 1-cocycles).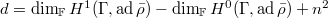 .
.
![$\phi: \mathcal{O}[ [X_1,\ldots, X_d] ]\rightarrow R^\Box$](./latex/latex2png-GaloisRepresentations_123969035_-5.gif) such that
such that 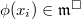 generate
generate 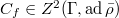 is a continuous 2-cocycle.
is a continuous 2-cocycle.
 is injective.
is injective.
![$R^\Box\cong \mathcal{O}[ [X_1,\ldots, X_d] ]$](./latex/latex2png-GaloisRepresentations_155578292_-5.gif) .
.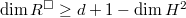 .
.![$R^\Box[1/\ell]_x^\wedge:= \lim_j R^\Box[1/\ell]/(\ker\phi_x[1/\ell])^j$](./latex/latex2png-GaloisRepresentations_170406041_-5.gif) pro-represents the functor
pro-represents the functor 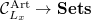 given by
given by 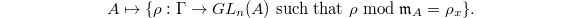
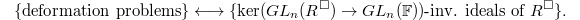
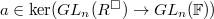 , then conjugation on
, then conjugation on 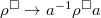 induces an action
induces an action 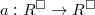 by the universal property.
by the universal property.
 is the full preimage of
is the full preimage of 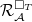 is represented by
is represented by 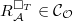 . When
. When 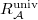 .
.
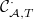 to be
to be ![$$\xymatrix@R=0cm@C=0.3cm{\mathcal{C}^0(G,\ad\bar\rho) \ar[r] \ar[rdd] & \mathcal{C}^1(G,\ad^0\bar\rho) \ar[r] \ar[rdd] & \mathcal{C}^2(G,\ad^0\bar\rho) \ar[r] & \mathcal{C}^3(G,\ad^0\bar\rho)\\ & \oplus & \oplus &\oplus \\& \mathcal{C}^0(G,\ad\bar\rho) \ar[r] \ar[rdd] & \displaystyle\bigoplus_{v\in T}\mathcal{C}^1(G_v,\ad^0\bar\rho) \ar[r] & \displaystyle\bigoplus_{v\in S}\mathcal{C}^2(G_v,\ad^0\bar\rho)\\ & & \oplus & &\\ & & \displaystyle\bigoplus_{v\in S\setminus T}\mathcal{C}^1(G_v,\ad^0\bar\rho)/\tilde{\mathcal{L}}(\mathcal{D}_v) \ar[ruu]& }$$](./latex/latex2png-GaloisRepresentations_256398670_.gif) Here
Here 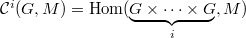 .
.
![$R_{\mathcal{A},T}^\mathrm{loc}[ [ X_1,\ldots, X_d] ]\twoheadrightarrow R_\mathcal{A}^{\Box_T}$](./latex/latex2png-GaloisRepresentations_18306381_-7.gif) . Here
. Here 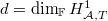 and the number of the relation is at most
and the number of the relation is at most 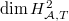 .
.
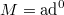 , then
, then ![\begin{align*}
\chi(G,M)-\sum_{v\in S}\chi(G_v,M)&=[F:\mathbb{Q}]\dim_\mathbb{F}M-\sum_{v\mid \infty}h^0(G_v, M)-\sum_{v\mid \ell}\dim_\mathbb{F}M [F_v: \mathbb{Q}_\ell]\\&=-\sum_{v\mid\infty}h^0(G_v,M).
\end{align*}](./latex/latex2png-GaloisRepresentations_247052606_.gif) (here we use the assumption that all primes above
(here we use the assumption that all primes above 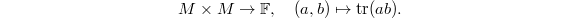 This gives identification
This gives identification 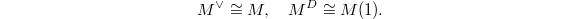
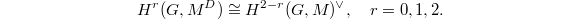
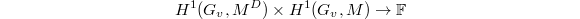 defines the dual
defines the dual 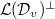 of
of 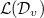 as the annihilator of
as the annihilator of ![$$\xymatrix{0 \ar[r] & H^0(G,M) \ar[r] & \oplus_{v\in S}H^0(G_v,M) \ar[r] & H^2(G,M^D)^\vee &\\
\ar[r] & H^1(G,M) \ar[r] & \oplus_{v\in S}H^1(G_v,M) \ar[r] & H^1(G,M^D)^\vee &\\
\ar[r] & H^2(G,M) \ar[r] & \oplus_{v\in S}H^2(G_v,M) \ar[r] & H^0(G,M^D)^\vee \ar[r] & 0\\}$$](./latex/latex2png-GaloisRepresentations_51080726_.gif)
![$R^\Box_{\bar\rho}[1/\ell]$](./latex/latex2png-GaloisRepresentations_76707535_-6.gif) (here the dimension is
(here the dimension is 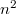 ) and
) and ![$R^\mathrm{univ}_{\bar\rho}[1/\ell]$](./latex/latex2png-GaloisRepresentations_170285479_-6.gif) if
if 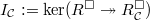 . Then
. Then 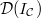 is a deformation problem.
is a deformation problem.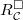 is equidimensional of dimension
is equidimensional of dimension 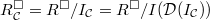 .
.![$\tau=[(1,0)]$](./latex/latex2png-GaloisRepresentations_47227376_-5.gif) of any dimension.
of any dimension.
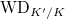 to be the category of WD-representations
to be the category of WD-representations 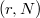 of
of 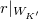 is unramified.
is unramified.
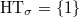 for any
for any 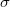 .
.
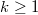 . The associated Galois representation
. The associated Galois representation 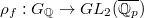 has
has 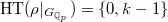 .
.
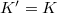 , which has only one component.
, which has only one component.