This is a rather sketchy (yet hopefully motivated) introduction to minimal models and the Enriques classification of complex algebraic surfaces. In the sequel, a surface means a smooth projective variety of dimension 2 over 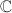 . Our main source is [1]. See also [2] and [3].
. Our main source is [1]. See also [2] and [3].
 Blow-ups and birational maps
Blow-ups and birational maps
Let  be a surface. The structure of rational maps between
be a surface. The structure of rational maps between  and any projective variety
and any projective variety 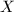 is simple by the following
is simple by the following
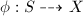 be a rational map. Then there exists a composite of finite many blow-ups
be a rational map. Then there exists a composite of finite many blow-ups 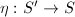 and a morphism
and a morphism 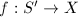 such that
such that 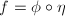 .
.
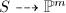 and linear systems on
and linear systems on  of dimension
of dimension 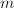 which has no fixed components. We use this correspondence and induct on the dimension of the linear systems. Each blow-up drops the dimension and this process terminates using the intersection pairing.
¡õ
which has no fixed components. We use this correspondence and induct on the dimension of the linear systems. Each blow-up drops the dimension and this process terminates using the intersection pairing.
¡õ
The structure of birational morphisms between surfaces is also rather simple. Suppose 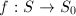 is a birational morphism of surfaces. Then
is a birational morphism of surfaces. Then 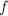 can be decomposed as a sequence of blow-ups
can be decomposed as a sequence of blow-ups 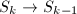 ,
, 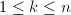 and an isomorphism
and an isomorphism  . Combining this fact with the elimination of indeterminacy, we obtain that
. Combining this fact with the elimination of indeterminacy, we obtain that
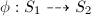 be a birational map between surfaces. Then there exists morphisms
be a birational map between surfaces. Then there exists morphisms 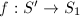 and
and 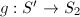 such that
such that 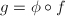 , where each of
, where each of 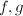 can be decomposed as a sequence of blow-ups and an isomorphism.
can be decomposed as a sequence of blow-ups and an isomorphism.
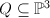 be a smooth quadric. The projection from a point
be a smooth quadric. The projection from a point 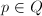 gives a birational map
gives a birational map 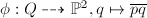 . Let
. Let 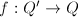 be the blow-up of
be the blow-up of 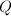 at
at 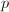 . We can identify
. We can identify 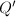 as
as 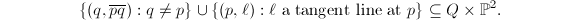 The composition
The composition 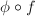 coincides with the projection onto the second factor
coincides with the projection onto the second factor 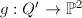 , which is also the blow-up of
, which is also the blow-up of 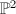 at the two points corresponding to the two lines on
at the two points corresponding to the two lines on 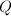 passing through
passing through 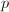 .
.
 Neron-Severi groups and minimal models
Neron-Severi groups and minimal models
The exponential exact sequence 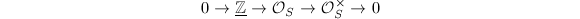 induces a long exact sequence
induces a long exact sequence 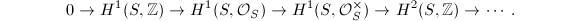 Hodge theory shows that
Hodge theory shows that 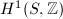 is a lattice in
is a lattice in 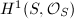 , so the Picard variety
, so the Picard variety 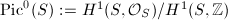 is a complex torus (and indeed an abelian variety). Since
is a complex torus (and indeed an abelian variety). Since 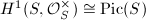 , we obtain an exact sequence
, we obtain an exact sequence 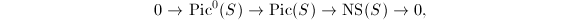 where
where 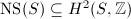 is the image of
is the image of 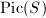 .
.
Since 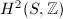 is finitely generated, the Neron-Severi group
is finitely generated, the Neron-Severi group 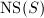 is also finitely generated. The rank
is also finitely generated. The rank 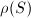 of
of 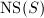 is called the Picard number of
is called the Picard number of  . The Neron-Severi group can also be described as the group of divisors on
. The Neron-Severi group can also be described as the group of divisors on  modulo algebraic equivalence ([3, V 1.7]).
modulo algebraic equivalence ([3, V 1.7]).
The behavior of the Neron-Severi group under a blow-up can be easily seen.
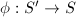 be a blow-up at a point with exceptional divisor
be a blow-up at a point with exceptional divisor 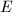 . Then there is a canonical isomorphism
. Then there is a canonical isomorphism ![$\NS(S')\cong \NS(S)\oplus \mathbb{Z}[E]$](./latex/latex2png-EnriquesClassification_181309615_-5.gif) .
.
![$\Pic(S)\oplus \mathbb{Z}[E]\cong\Pic(S')$](./latex/latex2png-EnriquesClassification_161532755_-5.gif) given by
given by 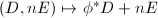 descends to the Neron-Severi groups.
¡õ
descends to the Neron-Severi groups.
¡õ
In other words, a blow-up increases the Picard number 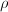 by 1. Thus the Neron-Severi group gives us a canonical order on the set
by 1. Thus the Neron-Severi group gives us a canonical order on the set 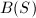 of isomorphism classes of surfaces birationally equivalent to a given surface
of isomorphism classes of surfaces birationally equivalent to a given surface  .
.
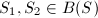 . We say that
. We say that 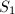 dominates
dominates 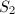 if there exists a birationally morphism
if there exists a birationally morphism 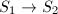 (in particular,
(in particular, 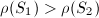 ). We say that
). We say that  is minimal if every birational morphism
is minimal if every birational morphism 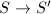 is an isomorphism.
is an isomorphism.
In particular, every surface dominates a minimal surface since the Picard number 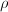 is finite. Conversely, every surface is obtained by a sequence of blow-ups of a minimal surface. So the problem of birational classification boils down to classifying minimal surfaces.
is finite. Conversely, every surface is obtained by a sequence of blow-ups of a minimal surface. So the problem of birational classification boils down to classifying minimal surfaces.
We can characterize minimal surfaces as those without exceptional curves. By the very definition of blow-ups, an exceptional curve 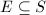 is isomorphic to
is isomorphic to 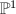 and has self-intersection number
and has self-intersection number 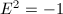 . This is actually a useful numerical criterion of minimality of surfaces ([1, II. 17]).
. This is actually a useful numerical criterion of minimality of surfaces ([1, II. 17]).
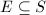 is isomorphic to
is isomorphic to 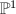 with
with 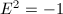 . Then
. Then 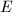 is an exceptional curve on
is an exceptional curve on  .
.
 Ruled surfaces
Ruled surfaces
In most cases, 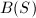 has a unique minimal element. However, the situation is not that simple for a large class of surfaces — ruled surfaces.
has a unique minimal element. However, the situation is not that simple for a large class of surfaces — ruled surfaces.
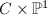 is a ruled surface. More generally, for any vector bundle
is a ruled surface. More generally, for any vector bundle 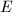 of rank two over the curve
of rank two over the curve 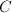 , the projective bundle
, the projective bundle 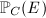 associated to
associated to 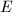 is a ruled surface due to the local trivialization. Every rational surface is ruled as it is birational to
is a ruled surface due to the local trivialization. Every rational surface is ruled as it is birational to 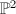 , hence birational to
, hence birational to 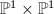 .
.
As a little digression, we can calculate several birational invariants for ruled surfaces easily.
 be any surface. We define
be any surface. We define
- the irregularity
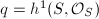 . It is equal to
. It is equal to 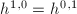 by Hodge theory. It is the dimension of the Picard variety
by Hodge theory. It is the dimension of the Picard variety 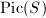 and the Albanese variety of
and the Albanese variety of  . It is also the difference
. It is also the difference 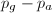 of the geometric genus and the arithmetic genus, hence its name.
of the geometric genus and the arithmetic genus, hence its name. - the geometric genus
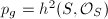 . It is equal to
. It is equal to 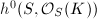 by Serre duality and
by Serre duality and 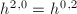 by Hodge theory.
by Hodge theory. - the plurigenus
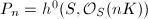 (
(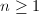 ).
).
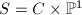 . Using the isomorphism
. Using the isomorphism 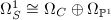 , we know that
, we know that 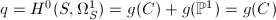 . Using the Künneth formula
. Using the Künneth formula 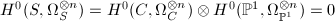 , we know that
, we know that 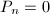 for all
for all 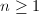 .
¡õ
.
¡õ
Now let us step back to the problem of finding the minimal models of ruled surfaces. This is closely related to the notion of geometrically ruled surfaces.
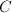 is a surface
is a surface  together with a smooth morphism
together with a smooth morphism 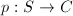 whose fibers are isomorphic to
whose fibers are isomorphic to 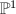 .
.
The first thing to notice is that geometrically ruled surfaces form a subclass of ruled surfaces due to the following theorem ([1, III.4]).
 be a surface together with a smooth morphism
be a surface together with a smooth morphism 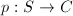 . If for some point
. If for some point 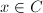 ,
, 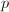 is smooth over
is smooth over 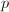 and
and 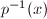 is isomorphic to
is isomorphic to 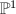 . Then there exists an open neighborhood
. Then there exists an open neighborhood 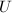 of
of  such that
such that 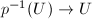 is a trivial
is a trivial 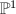 bundle. In particular, every geometrically ruled surface is ruled.
bundle. In particular, every geometrically ruled surface is ruled.
Also from the Noether-Enriques theorem, we know that every geometrically ruled surface over 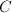 admits local trivializations as a
admits local trivializations as a 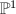 -bundle, thus they are are classified by the cohomology group
-bundle, thus they are are classified by the cohomology group 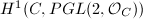 . The exact sequence
. The exact sequence 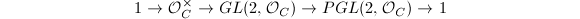 gives a long exact sequence
gives a long exact sequence 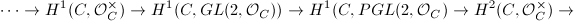 Since
Since 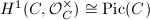 ,
, 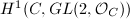 classifies rank 2 vector bundle over
classifies rank 2 vector bundle over 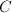 and
and 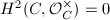 , one knows that every geometrically ruled surface over
, one knows that every geometrically ruled surface over 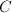 is actually
is actually 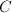 -isomorphic to
-isomorphic to 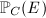 for some rank two vector bundle
for some rank two vector bundle 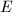 over
over 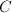 . Moreover, such
. Moreover, such  and
and 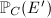 are
are 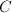 -isomorphic if and only if
-isomorphic if and only if 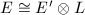 for some line bundle
for some line bundle 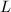 over
over 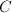 .
.
Now let us see how geometrically ruled surfaces play a significant role in classifying minimal ruled surfaces.
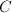 be a smooth irrational curve. Then the minimal models of
be a smooth irrational curve. Then the minimal models of 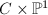 are geometrically rules surfaces over
are geometrically rules surfaces over 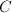 .
.
 is a minimal surface and
is a minimal surface and 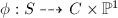 is a birational map. Then by elimination of indeterminacy, we can find another surface
is a birational map. Then by elimination of indeterminacy, we can find another surface 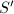 fitting in the following diagram
fitting in the following diagram ![$$\xymatrix{&S'\ar[dl]_f\ar[dr]^g &\\ S \ar@{-->}[rr]^-{\pi_1\circ\phi}& & C,}$$](./latex/latex2png-EnriquesClassification_160847498_.gif) where
where 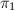 is the projection onto the first factor and
is the projection onto the first factor and 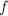 is a composition of
is a composition of 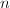 blow-ups. Suppose
blow-ups. Suppose 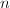 is the smallest such integer. If
is the smallest such integer. If 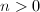 , let
, let 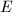 be the exceptional curve of the
be the exceptional curve of the 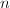 -th blow-up, then
-th blow-up, then 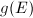 must be a point since
must be a point since 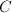 is irrational by assumption. So we can eliminate the
is irrational by assumption. So we can eliminate the 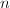 -th blow-up, which contradicts the minimality of
-th blow-up, which contradicts the minimality of 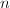 . Therefore
. Therefore 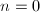 and
and 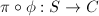 is actually a morphism with its generic fiber isomorphic to
is actually a morphism with its generic fiber isomorphic to 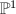 . Hence ([1, III.8])
. Hence ([1, III.8])  is a geometrically ruled surface over
is a geometrically ruled surface over 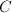 .
¡õ
.
¡õ
In other words, for an irrational ruled surface, its minimal models are not unique and are classified by those projective bundles 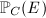 : the theory of rank two vector bundles
: the theory of rank two vector bundles 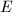 over a curve
over a curve 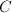 is delicate, but more or less understood.
is delicate, but more or less understood.
 Rational surfaces and Castelnuovo's theorem
Rational surfaces and Castelnuovo's theorem
The ruled surfaces with base curve 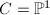 are called Hirzebruch surfaces. In particular, they are rational surfaces. Among these, the only geometrically ruled ones are
are called Hirzebruch surfaces. In particular, they are rational surfaces. Among these, the only geometrically ruled ones are 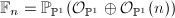 (
(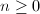 ) since every vector bundle over
) since every vector bundle over 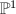 is a direct sum of line bundles. The above classification of minimal models of ruled surfaces fails for Hirzebruch surfaces. A calculation of intersection numbers on ruled surface implies the following result ([1, IV.1]).
is a direct sum of line bundles. The above classification of minimal models of ruled surfaces fails for Hirzebruch surfaces. A calculation of intersection numbers on ruled surface implies the following result ([1, IV.1]).
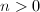 , then there is a unique irreducible curve on
, then there is a unique irreducible curve on 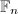 with negative self-intersection. Moreover, its self-intersection is
with negative self-intersection. Moreover, its self-intersection is 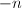 .
.
It follows that 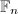 's are distinct and minimal for
's are distinct and minimal for 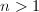 . However, it also follows that there is an irreducible curve
. However, it also follows that there is an irreducible curve 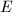 on
on 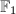 with
with 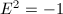 . Hence by the uniqueness,
. Hence by the uniqueness, 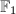 coincides with the blow-up of
coincides with the blow-up of 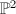 at one point, hence is not minimal.
at one point, hence is not minimal.
In order to find minimal models for rational surfaces, we need the following nontrivial fact ([1, V.6]). Notice that any rational surface satisfies 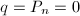 (
(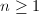 ).
).
Now we can deduce the following classification of minimal models of rational surfaces.
 be a minimal rational surfaces. By the lemma, there exists smooth curves
be a minimal rational surfaces. By the lemma, there exists smooth curves 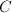 on
on  with the least nonnegative
with the least nonnegative 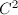 . Choose such a curve with the least
. Choose such a curve with the least 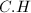 , where
, where 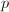 is a hyperplane section of
is a hyperplane section of  . Then using the minimality and Riemann-Roch, one can show that every divisor
. Then using the minimality and Riemann-Roch, one can show that every divisor 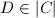 is a smooth rational curve. Since the linear system of curves of
is a smooth rational curve. Since the linear system of curves of 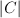 passing through
passing through 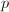 with multiplicity
with multiplicity 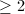 has codimension
has codimension 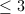 in
in 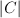 . We know that
. We know that 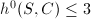 . Suppose
. Suppose 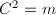 , then for any
, then for any 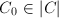 , the exact sequence
, the exact sequence 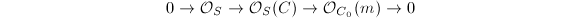 implies that
implies that 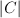 has no base point and
has no base point and 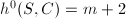 as
as 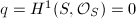 . Therefore
. Therefore 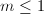 . When
. When 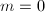 , the morphism
, the morphism 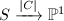 is geometrically ruled over
is geometrically ruled over 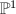 , hence
, hence  is
is 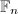 for some
for some 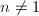 . When
. When 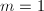 , each fiber of the morphism
, each fiber of the morphism 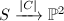 is the intersection of two distinct rational curves, hence a point. Therefore
is the intersection of two distinct rational curves, hence a point. Therefore 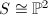 .
¡õ
.
¡õ
A similar argument using above useful lemma implies the following numerical characterization of rational surfaces ([1, V.1]).
Castelnuovo's Rationality Criterion together with the usage of Albanese varieties will enable us to finally show the uniqueness of the minimal models of all non-ruled surfaces ([1, V.19]).
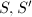 be two minimal non-ruled surfaces. Then every birational map between
be two minimal non-ruled surfaces. Then every birational map between  and
and 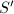 is an isomorphism. In particular, every non-ruled surface admits a unique minimal model.
is an isomorphism. In particular, every non-ruled surface admits a unique minimal model.
Hence we have found a complete list of minimal surfaces by now.
 Kodaira dimension
Kodaira dimension
Castelnuovo's Rationality Criterion provides a handy numerical tool to distinguish rational surfaces from others. We would like to see how the birational invariants will help us classifying surfaces. This can be achieved for ruled surfaces as well ([1, VI.18]).
In view of the important role played by the plurigenera, we introduce the notion of Kodaira dimension for a smooth projective variety.
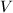 be a smooth projective variety and
be a smooth projective variety and 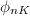 be the rational map from
be the rational map from 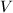 to the projective space associated to the complete linear system
to the projective space associated to the complete linear system 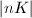 . We define the Kodaira dimension
. We define the Kodaira dimension 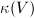 of
of 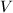 to be the maximal dimension of the images of
to be the maximal dimension of the images of 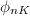 for
for 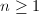 . We write
. We write 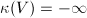 if
if 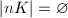 for
for 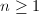 .
.
In particular, the Kodaira dimension 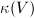 is always no greater than the dimension of
is always no greater than the dimension of 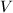 . Some examples are in order.
. Some examples are in order.
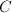 be a curve of genus
be a curve of genus 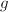 . Then Riemann-Roch implies the following correspondence:
. Then Riemann-Roch implies the following correspondence:
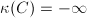 :
: 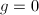 ,
,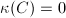 :
: 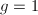 ,
,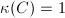 :
: 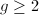 .
.
 be a surface. Then we have the following correspondence:
be a surface. Then we have the following correspondence:
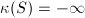 :
: 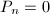 for
for 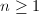 . By Enriques' theorem, these are exactly the ruled surfaces. Moreover, those with
. By Enriques' theorem, these are exactly the ruled surfaces. Moreover, those with 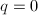 are exactly the rational surfaces,
are exactly the rational surfaces,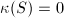 :
: 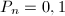 (not all 0),
(not all 0),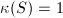 :
: 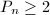 and
and 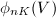 is a curve for some
is a curve for some 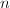 ,
,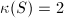 :
: 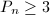 and
and 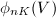 is a surface for some
is a surface for some 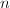 .
.
From this point of view, Kodaira dimension 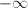 surfaces are analogous to rational curves, Kodaira dimension 0,1 surfaces are analogous to elliptic curves and Kodaira dimension 2 surfaces are analogous to curves of genus
surfaces are analogous to rational curves, Kodaira dimension 0,1 surfaces are analogous to elliptic curves and Kodaira dimension 2 surfaces are analogous to curves of genus 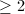 . For this reason we introduce the following piece of terminology.
. For this reason we introduce the following piece of terminology.
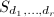 be a surface in
be a surface in 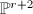 which is a complete intersection of hypersurfaces of degrees
which is a complete intersection of hypersurfaces of degrees 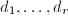 . Then as an application of the adjunction formula, we know that
. Then as an application of the adjunction formula, we know that
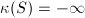 :
: 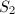 ,
, 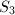 ,
, 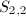 ,
,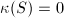 :
: 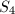 ,
, 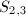 ,
, 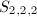 ,
,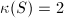 : all other cases.
: all other cases.
 Enriques classification
Enriques classification
To complete the Enriques classification, we shall name all remaining possibilities for surfaces of Kodaira dimension 0 and 1.
 is called elliptic if
is called elliptic if  is equipped with an elliptic fibration over some smooth curve
is equipped with an elliptic fibration over some smooth curve 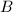 , i.e., there is a surjective morphism
, i.e., there is a surjective morphism 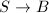 whose generic fiber is an elliptic curve.
whose generic fiber is an elliptic curve.
However, the converse is not true: the ruled surface 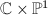 is elliptic but has Kodaira dimension
is elliptic but has Kodaira dimension 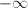 . An abelian surface which is an extension of two elliptic curves is also elliptic but has Kodaira dimension 0 (because any abelian surface has trivial canonical bundle).
. An abelian surface which is an extension of two elliptic curves is also elliptic but has Kodaira dimension 0 (because any abelian surface has trivial canonical bundle).
 is called hyperelliptic (or bielliptic) if
is called hyperelliptic (or bielliptic) if 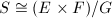 , where
, where 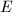 ,
, 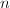 are two elliptic curves and
are two elliptic curves and 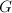 is a finite group of translations of
is a finite group of translations of 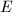 acting on
acting on 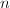 such that
such that  .
.
Hyperelliptic surfaces form another subclass of elliptic surfaces with 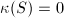 . Now we are in a position to classify all surfaces with
. Now we are in a position to classify all surfaces with 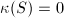 ([1, VIII.2]).
([1, VIII.2]).
 be a minimal surfaces with
be a minimal surfaces with 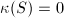 . Then there are four possibilities:
. Then there are four possibilities:
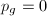 ,
, 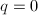 ; these are called Enriques surfaces,
; these are called Enriques surfaces,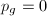 ,
, 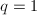 ; these are hyperelliptic surfaces,
; these are hyperelliptic surfaces,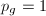 ,
, 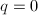 ; these are called K3 (Kummer-Kähler-Kodaira) surfaces,
; these are called K3 (Kummer-Kähler-Kodaira) surfaces,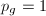 ,
, 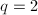 ; these are abelian surfaces.
; these are abelian surfaces.
A huge amount of geometry of these surfaces have been discovered since the 19th century, which may be the topic of another (sketchy) note.
So far we have complete the Enriques classification of minimal algebraic surfaces:
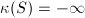 : ruled surfaces (including rational surfaces),
: ruled surfaces (including rational surfaces),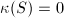 : Enriques surfaces, hyperelliptic surfaces, K3 surfaces, abelian surfaces,
: Enriques surfaces, hyperelliptic surfaces, K3 surfaces, abelian surfaces,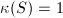 : elliptic surfaces (excluding the above two cases),
: elliptic surfaces (excluding the above two cases),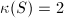 : surfaces of generic type.
: surfaces of generic type.
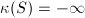 : surfaces of class VII,
: surfaces of class VII,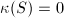 : complex tori (non-algebraic abelian surfaces), non-algebraic K3 surfaces, primary and secondary Kodaira surfaces,
: complex tori (non-algebraic abelian surfaces), non-algebraic K3 surfaces, primary and secondary Kodaira surfaces,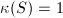 : non-algebraic elliptic surfaces.
: non-algebraic elliptic surfaces.
And also some extra classes in the case of characteristic 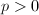 :
:
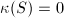 : non-classical Enriques surfaces (
: non-classical Enriques surfaces (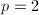 ), quasi-hyperelliptic (
), quasi-hyperelliptic (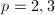 ),
),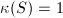 : quasi-elliptic surfaces (
: quasi-elliptic surfaces (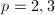 )
)
References
[1]Complex algebraic surfaces, Cambridge University Press, 1996.
[2]Complex Compact Surfaces, Springer, 2004.
[3]Algebraic Geometry, Springer, 2010.
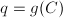 ,
, 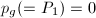 and
and  .
.
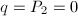 . Then there exists a smooth rational curve
. Then there exists a smooth rational curve 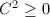 .
.
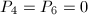 (or
(or 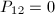 ). Then
). Then 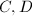 be two curves and
be two curves and 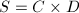 . From the example of curves, we know that
. From the example of curves, we know that
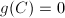 or
or 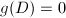 ,
,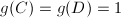 ,
,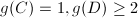 or
or 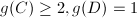 ,
,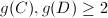 .
.