An elliptic surface is a surface that admits an elliptic fibration. Its generic fiber is an elliptic curve over a function field but special fibers may be singular. After giving the Kodaira-Neron classification of possible singular fibers and related geometric invariants, we build the neat connection between the geometry of elliptic surfaces and arithmetic of elliptic curves. This allows us to reprove the finite generation of the Mordell-Weil group of an elliptic curve and to further classify its possible rank and torsion using techniques from intersection theory and lattice theory. The theory of Mordell-Weil lattices plays an important role in finding elliptic curves over 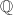 of high rank via specialization on elliptic surfaces. Our main sources are [1] and [2]. See also [3], [4] and [5]. This is a note prepared for the Baby Algebraic Geometry Seminar at Harvard.
of high rank via specialization on elliptic surfaces. Our main sources are [1] and [2]. See also [3], [4] and [5]. This is a note prepared for the Baby Algebraic Geometry Seminar at Harvard.
 Elliptic Surfaces
Elliptic Surfaces
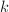 be an algebraically closed field and
be an algebraically closed field and 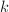 be a smooth projective curve over
be a smooth projective curve over 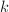 . An elliptic surface
. An elliptic surface 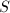 over
over 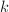 is a smooth projective surface
is a smooth projective surface 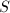 with an elliptic fibration over
with an elliptic fibration over 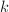 , i.e., a surjection
, i.e., a surjection 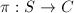 such that almost all fibers are smooth curves of genus 1.
such that almost all fibers are smooth curves of genus 1.
By definition, the generic fiber 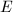 of an elliptic surface
of an elliptic surface 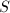 is a smooth curve of genus 1 over the function field
is a smooth curve of genus 1 over the function field 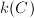 . Let
. Let 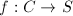 be a section of
be a section of 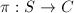 . Then
. Then 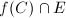 gives a rational point
gives a rational point 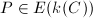 . Conversely, let
. Conversely, let 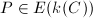 . Let
. Let 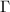 be the closure of
be the closure of 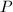 in
in 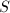 . We obtain a surjective birational morphism
. We obtain a surjective birational morphism 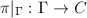 , which is an isomorphism since
, which is an isomorphism since 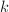 is smooth. In this way we have exhibited a bijection
is smooth. In this way we have exhibited a bijection 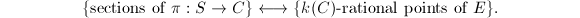
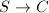 gives an elliptic curve
gives an elliptic curve 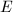 over
over 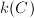 . We also make the convention that every elliptic surface has a singular fiber. So
. We also make the convention that every elliptic surface has a singular fiber. So 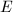 is a genuine elliptic curve over
is a genuine elliptic curve over 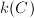 and cannot be defined over
and cannot be defined over 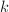 . In particular, this excludes trivial families of elliptic curves.
. In particular, this excludes trivial families of elliptic curves.
Given an elliptic curve 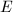 over
over 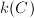 , there are different ways to extend
, there are different ways to extend 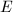 to an elliptic surface
to an elliptic surface 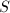 over
over 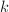 giving rise to the generic fiber. However, all these models are birational, so if we require that
giving rise to the generic fiber. However, all these models are birational, so if we require that 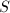 is relatively minimal, i.e., the fibers do not contain
is relatively minimal, i.e., the fibers do not contain 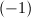 -curves, then
-curves, then 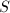 is unique up to isomorphism (the uniqueness will follow from the classification of singular fibers, see [4, II.1.2]). We obtain the following correspondence:
is unique up to isomorphism (the uniqueness will follow from the classification of singular fibers, see [4, II.1.2]). We obtain the following correspondence: 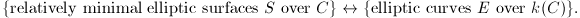 The explicit description of the relatively minimal model is given by Kodaira in characteristic 0 and by Neron in general. The elliptic surface thus associated to
The explicit description of the relatively minimal model is given by Kodaira in characteristic 0 and by Neron in general. The elliptic surface thus associated to 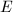 is sometimes called the Kodaira-Neron model of
is sometimes called the Kodaira-Neron model of 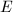 .
.
As already alluded, the theme of this talk is to relate the geometry of the elliptic surface 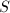 and the arithmetic of the elliptic curve
and the arithmetic of the elliptic curve 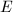 .
.
 The Kodaira-Neron Model
The Kodaira-Neron Model
How do the singular fibers of an elliptic surface look like? There are many ways to classify the possible singular fibers. Here we use the explicit equations.
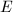 be the elliptic curve over
be the elliptic curve over 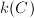 . We work locally and take a local parameter
. We work locally and take a local parameter 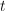 . Assume
. Assume 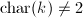 for simplicity, then
for simplicity, then 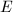 is given by the Weierstrass equation
is given by the Weierstrass equation 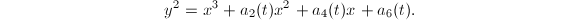 Assume we have a singular fiber at
Assume we have a singular fiber at 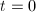 . Moving the singularity to
. Moving the singularity to 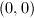 , we know that
, we know that 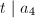 and
and 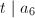 . We change notation and write
. We change notation and write 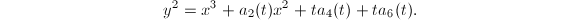 So if this equation defines an elliptic surface, then we know the singular fiber is either a nodal cubic curve (if
So if this equation defines an elliptic surface, then we know the singular fiber is either a nodal cubic curve (if 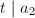 ) or a cusp cubic curve (if
) or a cusp cubic curve (if 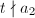 ). These are called multiplicative and additive reduction (due to their group structures) and the Kodaira symbols are
). These are called multiplicative and additive reduction (due to their group structures) and the Kodaira symbols are  and II respectively.
and II respectively.
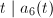 .
.
- Suppose
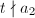 . Then
. Then 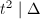 . Let us consider the case
. Let us consider the case 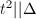 for simplicity, then translating
for simplicity, then translating 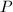 gives
gives 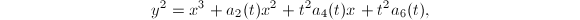 where
where 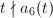 . Now we blow up
. Now we blow up  with
with 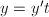 ,
, 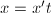 , to get
, to get 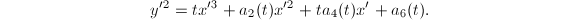 One can check that the surface singularity is resolved and the fiber at
One can check that the surface singularity is resolved and the fiber at  is the strict transform of the nodal cubic curve (a rational curve) together with the rational exceptional divisor given by
is the strict transform of the nodal cubic curve (a rational curve) together with the rational exceptional divisor given by 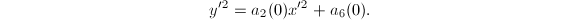 This singular fiber type is denoted by
This singular fiber type is denoted by 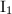 . More generally, when higher powers of
. More generally, when higher powers of 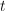 divide
divide 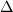 , we need to blow-up multiple times to resolve the surface singularity. The resulting singular type is denoted by
, we need to blow-up multiple times to resolve the surface singularity. The resulting singular type is denoted by 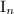 , an
, an 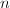 -polygon of rational curves.
-polygon of rational curves. - Suppose
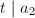 . Then the first blow-up has three possibilities:
. Then the first blow-up has three possibilities:
- a rational point meeting the strict transform of the cuspidal curve tangentially at 1 point (Type III);
- two lines meeting the strict transform of the cuspidal curve at 1 point (Type IV);
- a double line (Type
 )
)
It may not be a good idea if I keep on blowing-up for 3 hours. Let me tell you the result instead. In fact, one can determine the singular type from the equation using the so-called Tate's algorithm over any perfect field, as demonstrated above.
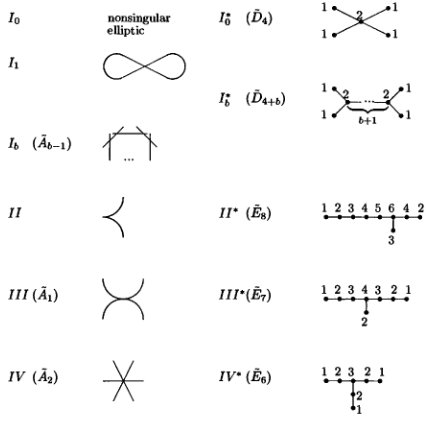 |
| Kodaira-Neron classification |
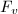 , which is either
, which is either 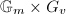 or
or 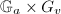 . Here
. Here 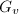 is the component group associated to a singular fiber
is the component group associated to a singular fiber 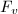 , which is a finite abelian group.
, which is a finite abelian group.
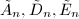 . Removing the simple component meeting the zero section, we obtain exactly the Dynkin diagrams
. Removing the simple component meeting the zero section, we obtain exactly the Dynkin diagrams 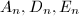 . These are root systems with roots of the same length
. These are root systems with roots of the same length 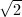 and correspond to even positive definite lattices, with determinants
and correspond to even positive definite lattices, with determinants 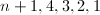 respectively. Miraculously, the determinants are exactly equal to the number of simple components, i.e., the order of
respectively. Miraculously, the determinants are exactly equal to the number of simple components, i.e., the order of 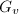 . Notice that
. Notice that 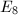 is unimodular which ends up to be important for us. In fact, a basic result from lattice theory is that
is unimodular which ends up to be important for us. In fact, a basic result from lattice theory is that 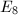 is the unique unimodular even positive definite lattice with rank
is the unique unimodular even positive definite lattice with rank 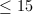 .
.
 Neron-Severi groups and Mordell-Weil groups
Neron-Severi groups and Mordell-Weil groups
Write 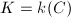 for short. A point
for short. A point 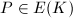 determines a section of
determines a section of 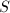 . Denote the image curve by
. Denote the image curve by 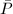 . A point
. A point 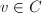 also gives us a divisor
also gives us a divisor 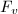 , the fiber above
, the fiber above 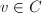 . Every divisor on the elliptic surfaces
. Every divisor on the elliptic surfaces 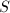 can be written as the sum of such horizontal and vertical divisors. Let
can be written as the sum of such horizontal and vertical divisors. Let 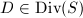 be an divisor, then we can decompose
be an divisor, then we can decompose 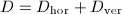 . The horizontal part
. The horizontal part 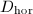 intersects
intersects 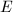 at a divisor on
at a divisor on 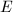 , which gives a point
, which gives a point 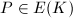 using the group law. So we have a map
using the group law. So we have a map 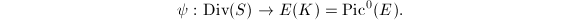 The kernel of
The kernel of 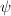 is
is 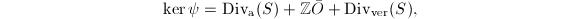 where
where 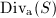 is the group of divisors algebraically equivalent to 0. To see that
is the group of divisors algebraically equivalent to 0. To see that 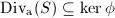 , we use the fact ([4, VII.1.1]) that
, we use the fact ([4, VII.1.1]) that 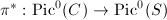 is an isomorphism to conclude that any divisor in
is an isomorphism to conclude that any divisor in 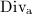 is linearly equivalent to a vertical divisor in
is linearly equivalent to a vertical divisor in 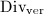 . So we obtained that
. So we obtained that
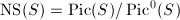 be the Neron-Severi group of
be the Neron-Severi group of 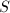 , i.e., the divisors modulo algebraic equivalence. Let
, i.e., the divisors modulo algebraic equivalence. Let 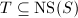 be the subgroup generated by
be the subgroup generated by  and vertical divisors. Then
and vertical divisors. Then 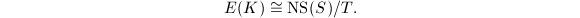
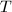 is called the trivial lattice for the obvious reason.
is called the trivial lattice for the obvious reason.
This theorem relates the arithmetic of 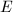 and the geometry of
and the geometry of 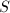 . It is well-known that the Neron-Severi group
. It is well-known that the Neron-Severi group 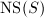 is finitely generated for any smooth projective variety (the theorem of the base). Consequently, we have reproved the Mordell-Weil theorem using an argument of geometric nature.
is finitely generated for any smooth projective variety (the theorem of the base). Consequently, we have reproved the Mordell-Weil theorem using an argument of geometric nature.
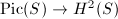 . We have an intersection pairing on
. We have an intersection pairing on 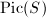 and a cup product pairing on
and a cup product pairing on 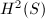 . The cycle map preserves the pairings, hence its kernel is the group of divisors numerically equivalent to 0. Using Riemann-Roch, one can show that numerical equivalence and algebraic equivalence are the same on an elliptic surface, hence
. The cycle map preserves the pairings, hence its kernel is the group of divisors numerically equivalent to 0. Using Riemann-Roch, one can show that numerical equivalence and algebraic equivalence are the same on an elliptic surface, hence 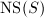 itself embeds into the finite dimensional vector space
itself embeds into the finite dimensional vector space 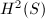 , In particular.
, In particular. 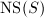 is finitely generated and even torsion-free.
is finitely generated and even torsion-free.
Our next goal is to further study the structure of 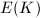 (e.g., its rank and torsion) using the geometry of
(e.g., its rank and torsion) using the geometry of 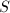 .
.
The number 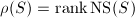 is called the Picard number of
is called the Picard number of 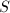 . By the Hodge index theorem, the lattice
. By the Hodge index theorem, the lattice 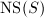 equipped with the intersection pairing has signature
equipped with the intersection pairing has signature 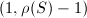 . We immediately find the following bound on the rank of
. We immediately find the following bound on the rank of 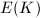 :
:
As discussed above, 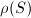 is bounded above by
is bounded above by 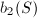 , the second Betti number (it is even bounded by
, the second Betti number (it is even bounded by  if
if 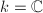 ). So we need more knowledge about the trivial lattice
). So we need more knowledge about the trivial lattice 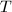 .
.
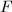 : a generic fiber
: a generic fiber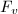 : the fiber above
: the fiber above 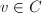
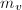 : the number of components of
: the number of components of 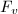
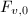 : the identity component of
: the identity component of 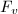
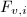 : the
: the 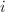 -th non-identity component of
-th non-identity component of 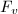 ,
, 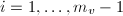
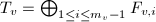 : the subgroup of
: the subgroup of 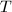 generated non-identity components of
generated non-identity components of 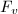
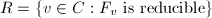
Because all fibers are algebraically equivalent, we know that 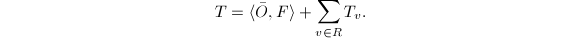 Note that the intersection matrix of
Note that the intersection matrix of 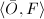 is
is 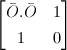 which is non-degenerate with determinant
which is non-degenerate with determinant 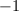 and signature
and signature 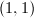 . Also,
. Also, 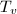 is a root lattice of type
is a root lattice of type 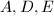 , hence the intersection matrix, denoted by
, hence the intersection matrix, denoted by 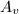 , is negative definite. Therefore, the above decomposition of
, is negative definite. Therefore, the above decomposition of 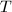 is actually a direct sum. It follows that
is actually a direct sum. It follows that
Therefore we can really compute the rank of 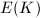 as long as we know all the singular fibers. Conversely, knowing the possible rank of
as long as we know all the singular fibers. Conversely, knowing the possible rank of 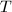 will help us to classify configurations of singular fibers of elliptic surfaces.
will help us to classify configurations of singular fibers of elliptic surfaces.
 Height Pairings
Height Pairings
How about the torsion? The crucial idea is to endow 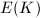 a height pairing. We already know that
a height pairing. We already know that 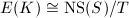 and
and 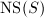 possesses an intersection pairing. So it is natural to construct a splitting of this isomorphism so that we can embed
possesses an intersection pairing. So it is natural to construct a splitting of this isomorphism so that we can embed 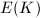 into
into 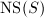 .
.
We need the following theorem due to Kodaira.
The following is not quite a ``splitting'', nonetheless is good enough for our purpose.
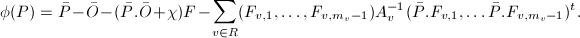 This is easily verified by taking the intersection pairing of
This is easily verified by taking the intersection pairing of 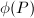 and the basis elements of the trivial lattice
and the basis elements of the trivial lattice 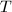 together with the canonical bundle formula. The reason we need to tensor with
together with the canonical bundle formula. The reason we need to tensor with 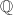 is that the coefficients may not be integers.
¡õ
is that the coefficients may not be integers.
¡õ
One can check that 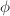 is also a group homomorphism. So we can define a pairing on
is also a group homomorphism. So we can define a pairing on 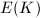 using the pairing on
using the pairing on 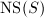 .
.
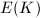 by
by 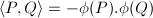 . We add a sign in order to make the height pairing positive definite.
. We add a sign in order to make the height pairing positive definite.
The following is easily deduced.
Now from the explicit formula for 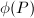 , we can also write down the height pairing explicitly,
, we can also write down the height pairing explicitly, 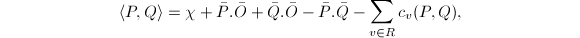 where
where 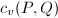 is a positive number only depending on the the fiber components of
is a positive number only depending on the the fiber components of 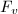 meeting
meeting 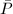 and
and 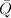 .
.
We can apply the height pairing to deduce some information about torsion groups. Recall that 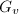 is the component group of the singular fiber
is the component group of the singular fiber 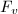 . The map
. The map 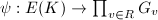 sending a section to the simple fiber components it meets is a group homomorphism.
sending a section to the simple fiber components it meets is a group homomorphism.
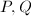 have the same image. Then
have the same image. Then 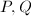 meets the same simple components, hence
meets the same simple components, hence 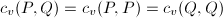 . Because
. Because 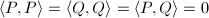 , from the above explicit formula we conclude that
, from the above explicit formula we conclude that 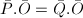 and
and 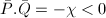 . Hence
. Hence 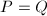 .
¡õ
.
¡õ
In this way, the singular types of the elliptic surface  impose very strong constraints on the torsion group of
impose very strong constraints on the torsion group of  , and vice versa.
, and vice versa.
 Mordell-Weil Lattices
Mordell-Weil Lattices
How can we identify 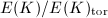 with a sublattice of
with a sublattice of 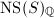 ? A bit of lattice-theoretic and intersection-theoretic computation gives the precise answer as long as
? A bit of lattice-theoretic and intersection-theoretic computation gives the precise answer as long as 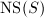 is unimodular.
is unimodular.
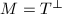 be the complementary lattice of
be the complementary lattice of 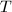 in
in 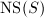 (called the essential lattice) and
(called the essential lattice) and 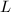 be the opposite lattice of
be the opposite lattice of 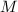 . Then
. Then 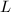 is an even positive definite lattice. Suppose
is an even positive definite lattice. Suppose 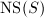 is unimodular. Then
is unimodular. Then 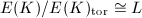 as lattices.
as lattices.
We now step toward the case study of rational elliptic surfaces, where the lattice-theoretic method has achieved huge success in classifying all possible structures of 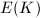 .
.
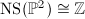 is unimodular. Since each blow-up changes the determinant of
is unimodular. Since each blow-up changes the determinant of 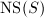 by
by 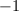 due to the exceptional divisor, we know that
due to the exceptional divisor, we know that 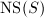 is also unimodular. Because
is also unimodular. Because 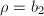 for a rational surface, it suffices to check that
for a rational surface, it suffices to check that 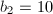 . This follows from the middle row (0,10,0) of the Hodge diamond.
¡õ
. This follows from the middle row (0,10,0) of the Hodge diamond.
¡õ
Here comes a clever way to classify 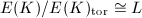 relying on the fact there is only one unimodular even positive definite lattice of rank 8, namely the root lattice
relying on the fact there is only one unimodular even positive definite lattice of rank 8, namely the root lattice 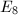 . Consider the complementary lattice
. Consider the complementary lattice 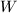 of the rank 2 sublattice
of the rank 2 sublattice 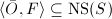 . Then
. Then 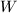 is unimodular, even and positive definite, so it must be
is unimodular, even and positive definite, so it must be 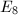 ! Since
! Since 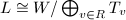 and each
and each 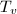 is a root lattice. We only need to find all possible embeddings of a root lattice into
is a root lattice. We only need to find all possible embeddings of a root lattice into 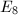 . If you know
. If you know 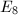 , it is just so simple — there are only 74 cases. All the possible shapes of
, it is just so simple — there are only 74 cases. All the possible shapes of 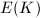 are beautifully classified by Oguiso and Shioda [6].
are beautifully classified by Oguiso and Shioda [6].
 of high rank via specialization. A theorem of Neron ensures that the ranks of infinitely many specializations do not go down. Indeed, all rank records so far are obtained this way (together with searching techniques). The maximal rank of the Mordell-Weil lattice of a rational elliptic surface is 8, as we have seen, and Neron used it to find infinitely many elliptic curves with rank at least 11. Elkies stepped further and used elliptic K3 surfaces with maximal Mordell-Weil rank 17 to find the current record curve with rank
of high rank via specialization. A theorem of Neron ensures that the ranks of infinitely many specializations do not go down. Indeed, all rank records so far are obtained this way (together with searching techniques). The maximal rank of the Mordell-Weil lattice of a rational elliptic surface is 8, as we have seen, and Neron used it to find infinitely many elliptic curves with rank at least 11. Elkies stepped further and used elliptic K3 surfaces with maximal Mordell-Weil rank 17 to find the current record curve with rank 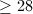 . This story probably is the theme of a different talk.
. This story probably is the theme of a different talk.
References
[1]Elliptic Surfaces, Arxiv preprint arXiv:0907.0298 (2009).
[2]On the Mordell-Weil lattices, Comment. Math. Univ. St. Paul 39 (1990), no.2, 211--240.
[3]Three lectures on elliptic surfaces and curves of high rank, Arxiv preprint arXiv:0709.2908 (2007).
[4]The basic theory of elliptic surfaces, ETS Editrice Pisa, 1989.
[5]K3 surfaces of high rank, Harvard University Cambridge, Massachusetts, 2006.
[6]The Mordell-Weil lattice of a rational elliptic surface, Comment. Math. Univ. St. Paul 40 (1991), no.1, 83--99.
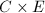 is an elliptic surface.
is an elliptic surface.
![$$y^2=x^3+a_2(t)x^2+a_4(t)x+a_6(t),\quad a_i(t)\in k[t]$$](./latex/latex2png-EllipticSurfaces_100732817_.gif) defines an elliptic surface over
defines an elliptic surface over 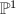 as long as it is smooth.
as long as it is smooth.
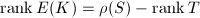 .
.
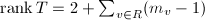 .
.
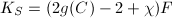 ,
, 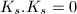 and for any
and for any 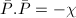 , where
, where 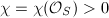 .
.
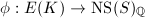 such that
such that 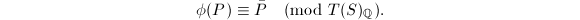
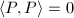 if and only if
if and only if 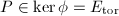 .
.
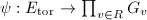 is injective.
is injective.
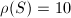 .
.
![\begin{center}
\begin{tabular}[h]{|c|c|}
$E(K)_\mathrm{tor}$ & $r=\rank E(K)$\\\hline
$0$ & $0\le r\le 8$\\
$\mathbb{Z}/2 \mathbb{Z}$ & $0\le r\le 4$\\
$\mathbb{Z}/3 \mathbb{Z}$ & $0\le r\le 2$\\
$\mathbb{Z}/2 \mathbb{Z}\times\mathbb{Z}/2 \mathbb{Z}$ & $0\le r\le 2$\\
$\mathbb{Z}/4 \mathbb{Z}$ & $0\le r\le 1$\\
$\mathbb{Z}/5 \mathbb{Z}$ & $0$\\
$\mathbb{Z}/6 \mathbb{Z}$ & $0$\\
$\mathbb{Z}/4 \mathbb{Z}\times \mathbb{Z}/2 \mathbb{Z}$ & $0$\\
$\mathbb{Z}/3 \mathbb{Z}\times \mathbb{Z}/3 \mathbb{Z}$ & $0$
\end{tabular}
\end{center}](./latex/latex2png-EllipticSurfaces_221369468_.gif)