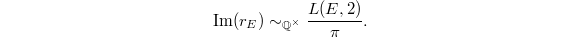Euler in 1735 discovered that 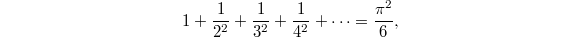 and Dirichlet in 1839 proved that
and Dirichlet in 1839 proved that 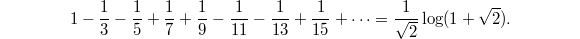 We begin by re-interpreting these sums as special values of
We begin by re-interpreting these sums as special values of  -functions of number fields. The notion of
-functions of number fields. The notion of 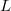 -functions has been vastly generalized and their special values are the subject of the celebrated conjectures of Birch-Swinnerton-Dyer, Beilinson and many others. We then focus on the next simplest (but incredibly rich) case: the
-functions has been vastly generalized and their special values are the subject of the celebrated conjectures of Birch-Swinnerton-Dyer, Beilinson and many others. We then focus on the next simplest (but incredibly rich) case: the 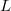 -function
-function 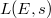 of an elliptic curve
of an elliptic curve 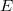 . In 1970s, Bloch discovered a beautiful formula for
. In 1970s, Bloch discovered a beautiful formula for 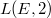 in terms of Wigner's dilogarithm function (a generalization of the usual logarithm). We illustrate this formula with explicit examples and explain how Quillen's
in terms of Wigner's dilogarithm function (a generalization of the usual logarithm). We illustrate this formula with explicit examples and explain how Quillen's 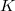 -group
-group 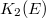 plays a surprising role in calculating
plays a surprising role in calculating 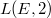 .
.
This is a note I prepared for my fourth Trivial Notions talk at Harvard, Spring 2015. Our main sources are [1], [2], [3], [4], [5] and [6].
 Riemann and Dedekind zeta function
Riemann and Dedekind zeta function
Euler's identity 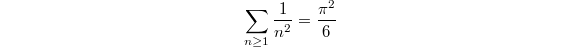 and other similar identities like
and other similar identities like 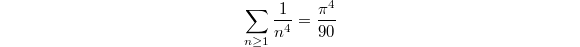 can be viewed as the special value at
can be viewed as the special value at 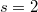 ,
, 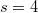 of the Riemann zeta function
of the Riemann zeta function 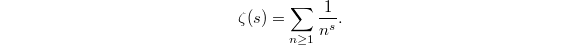 This sum converges when
This sum converges when 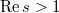 and the basic observation due to Riemann is that
and the basic observation due to Riemann is that  can be extended as a meromorphic function on
can be extended as a meromorphic function on  on via analytic continuation. It is holomorphic everywhere except a simple pole at
on via analytic continuation. It is holomorphic everywhere except a simple pole at 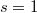 with residue
with residue 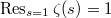 .
.
Here are two key properties of 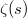 . It has an Euler product when
. It has an Euler product when 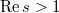 , essentially due to the fundamental theorem of arithmetics in
, essentially due to the fundamental theorem of arithmetics in 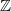 :
: 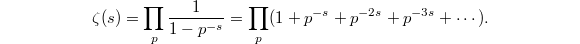 It satisfies a functional equation, also established by Riemann, relating
It satisfies a functional equation, also established by Riemann, relating 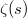 and
and 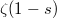 :
: 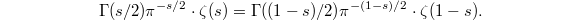 The analytic continuation endows the famous formula
The analytic continuation endows the famous formula 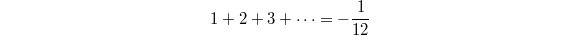 a mathematical meaning by interpreting the left hand side as
a mathematical meaning by interpreting the left hand side as 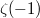 , which can be easily computed by the functional equation and the value
, which can be easily computed by the functional equation and the value 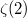 .
.
By replacing 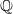 with arbitrary number field
with arbitrary number field 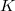 , we obtain the Dedekind zeta function,
, we obtain the Dedekind zeta function, 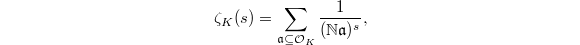 which has a similar Euler product by replacing prime numbers by prime ideals of
which has a similar Euler product by replacing prime numbers by prime ideals of 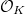 . It also has analytic continuation and a functional equation. If you ever wonder what analytic continuation does any good for you besides computing the sum of all natural numbers:
. It also has analytic continuation and a functional equation. If you ever wonder what analytic continuation does any good for you besides computing the sum of all natural numbers:
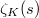 at
at 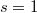 is equal to
is equal to 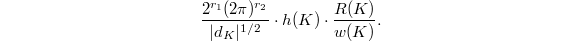 Here
Here
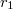 and
and 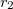 are the number of real and complex places of
are the number of real and complex places of 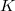 .
.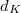 is the discriminant of
is the discriminant of 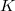 .
.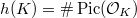 is the class number.
is the class number.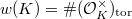 is the number of roots of unity.
is the number of roots of unity.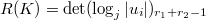 is the regulator, where
is the regulator, where 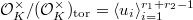 .
.
To summarize: you first collect all local information about 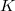 (at all primes of
(at all primes of 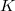 ) and form the Euler product, then running the mysterious process of analytic continuation pops out deep global information about
) and form the Euler product, then running the mysterious process of analytic continuation pops out deep global information about 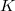 for you!
for you!
 Dirichlet L-functions
Dirichlet L-functions
Analogously, Dirichlet's identity can be viewed as the special value at 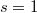 of the Dirichlet
of the Dirichlet 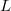 -function
-function 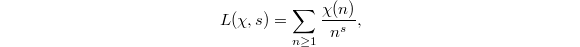 where
where 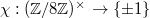 is a group homomorphism with
is a group homomorphism with 
The sum converges when 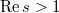 and can be analytic continued to a holomorphic function on
and can be analytic continued to a holomorphic function on 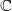 . The multiplicativity of
. The multiplicativity of 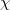 also gives an Euler product
also gives an Euler product 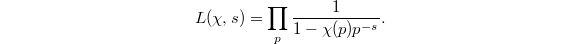 The key observation is that one can also view
The key observation is that one can also view 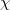 as the the Legendre symbol
as the the Legendre symbol 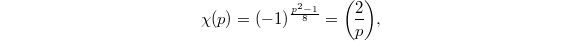 whose value dictates the splitting behavior of
whose value dictates the splitting behavior of 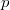 in
in 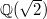 . Therefore
. Therefore
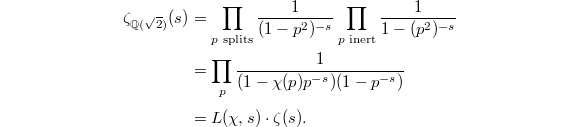 Now comparing the residues at
Now comparing the residues at 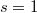 on both sides we obtain Dirichlet's formula that
on both sides we obtain Dirichlet's formula that 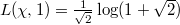 in the beginning! To summarize: Dirichlet's formula is simply the consequence of the class number formula together with the key that
in the beginning! To summarize: Dirichlet's formula is simply the consequence of the class number formula together with the key that 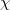 is linked to "arithmetic".
is linked to "arithmetic".
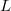 -function can be defined as a sum
-function can be defined as a sum 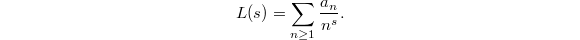 But if you put random
But if you put random 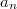 there it is hopeless to get you hands on.
there it is hopeless to get you hands on. 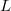 -functions people studied a lot involves two major sources of
-functions people studied a lot involves two major sources of 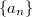 : coming form algebraic varieties/Galois representations (Dedekind, Artin, Hasse-Weil, ...) or coming from modular forms/automorphic representations (Dirichlet, Hecke, ...). It is hard to define precisely what a general
: coming form algebraic varieties/Galois representations (Dedekind, Artin, Hasse-Weil, ...) or coming from modular forms/automorphic representations (Dirichlet, Hecke, ...). It is hard to define precisely what a general 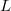 -function is, but you know one when you see one: in particular it should have an Euler product and should satisfy a certain functional equation. The first class of
-function is, but you know one when you see one: in particular it should have an Euler product and should satisfy a certain functional equation. The first class of 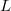 -functions (motivic
-functions (motivic 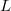 -functions) has natural definition as Euler products but the functional equation and analytic continuation are hard to establish, while the second class of
-functions) has natural definition as Euler products but the functional equation and analytic continuation are hard to establish, while the second class of 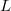 -functions (automorphic
-functions (automorphic 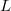 -functions) are harder to construct but has more accessible analytic property once constructed. One major motivation of the Langlands program is trying to relate these two sources of
-functions) are harder to construct but has more accessible analytic property once constructed. One major motivation of the Langlands program is trying to relate these two sources of 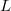 -functions.
-functions.
 L-function of elliptic curves
L-function of elliptic curves
Now let 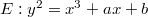 be an elliptic curve over
be an elliptic curve over 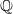 . To define its
. To define its 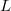 -function, we would like to first collect the local information about
-function, we would like to first collect the local information about 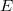 . The natural choice is to look at the number of its
. The natural choice is to look at the number of its 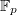 -rational points (we will systematically ignore bad reduction in this talk). It is a theorem of Hasse that
-rational points (we will systematically ignore bad reduction in this talk). It is a theorem of Hasse that 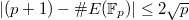 . Let
. Let 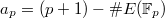 be the error term. The Hasse-Weil
be the error term. The Hasse-Weil 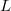 -function of
-function of 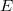 is then defined to be
is then defined to be 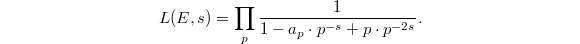 The sum converges when
The sum converges when 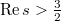 due to Hasse's bound. The definition looks familiar except that the denominator becomes a quadratic polynomial rather than a linear polynomial in
due to Hasse's bound. The definition looks familiar except that the denominator becomes a quadratic polynomial rather than a linear polynomial in 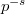 (since we are looking at a motive of rank 2).
(since we are looking at a motive of rank 2).
The most interesting global information about 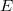 is its rational points
is its rational points 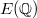 , which is a finitely generated abelian group by Mordell-Weil. Does
, which is a finitely generated abelian group by Mordell-Weil. Does 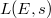 give any hint about it? Let us try to plug in
give any hint about it? Let us try to plug in 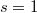 formally:
formally: 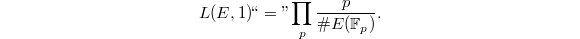 Since each point in
Since each point in 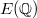 reduces to a point in
reduces to a point in 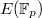 , when
, when 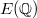 has large rank
has large rank 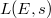 tends to be small. Moreover, the rate of
tends to be small. Moreover, the rate of 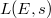 converging to zero should be related to
converging to zero should be related to 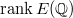 ! In 1960s, Birch and Swinnerton-Dyer did numerical experiments on EDSAC and suggested the heuristic
! In 1960s, Birch and Swinnerton-Dyer did numerical experiments on EDSAC and suggested the heuristic 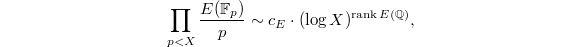 which leads to the famous conjecture that
which leads to the famous conjecture that
Now it is a theorem that 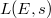 has analytic continuation to
has analytic continuation to 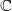 (and satisfies a functional equation relating
(and satisfies a functional equation relating 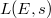 and
and 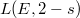 ), so the BSD conjecture actually makes sense. The proof of this hard theorem is via the famous modularity theorem due to Wiles, Taylor, Breuil, Conrad and Diamond: there exists
), so the BSD conjecture actually makes sense. The proof of this hard theorem is via the famous modularity theorem due to Wiles, Taylor, Breuil, Conrad and Diamond: there exists 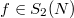 (weight 2 cusp newform of level
(weight 2 cusp newform of level 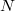 ) such that
) such that 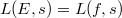 . The following example may illustrate how nontrivial this modularity theorem is.
. The following example may illustrate how nontrivial this modularity theorem is.
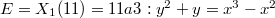 . Counting points over
. Counting points over 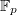 we can tabulate the first few
we can tabulate the first few 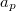 's.
's.
![\begin{center}
\begin{tabular}[h]{*{16}{|>{$}c<{$}}|}
p & 2& 3& 5& 7& 11& 13& 17& 19& 23& 29& 31& 37& 41& 43& 47\\\hline
a_p & -2& -1& 1& -2& 1& 4& -2& 0& -1& 0& 7& 3& -8& -6& 8\\
\end{tabular}
\end{center}](./latex/latex2png-BeilinsonBloch_173439349_.gif) On the other hand, the modularity theorem ensures
On the other hand, the modularity theorem ensures 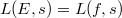 for some
for some 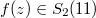 . It turns out
. It turns out 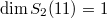 . The unique such form has the classical eta product
. The unique such form has the classical eta product
 One now can have infinite fun checking the coefficient before
One now can have infinite fun checking the coefficient before 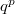 actually agrees with
actually agrees with 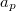 ! It is far from obvious why this power series expansion should have anything to do with solving the cubic equation
! It is far from obvious why this power series expansion should have anything to do with solving the cubic equation 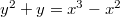 over all finite fields.
over all finite fields.
 L(E,2)
L(E,2)
Though important progresses toward it have been made, the BSD conjecture is still widely open. In some sense the value of 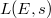 at
at 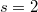 is more accessible than
is more accessible than 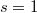 since it does not involve the process of analytic continuation. Our next goal is to illustrate Bloch and Beilinson's theorem on the special value
since it does not involve the process of analytic continuation. Our next goal is to illustrate Bloch and Beilinson's theorem on the special value 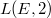 .
.
The idea is to generalize the logarithm appearing in Dirichlet's formula to the dilogarithm.
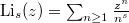 . In particular
. In particular 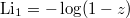 . It converges when
. It converges when 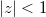 and like the logarithm, it can be analytic continued to obtain a multi-valued function on
and like the logarithm, it can be analytic continued to obtain a multi-valued function on 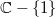 . The dilogarithm jumps by
. The dilogarithm jumps by 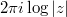 as
as  go around
go around 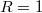 . To obtain a single valued function, we modify the dilogarithm and define the Bloch-Wigner dilogarithm
. To obtain a single valued function, we modify the dilogarithm and define the Bloch-Wigner dilogarithm 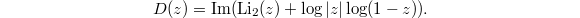 It becomes a continuous single-valued function on
It becomes a continuous single-valued function on 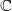 , real analytic on
, real analytic on 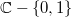 (with singular type
(with singular type 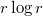 ), vanish on the real line and satisfies
), vanish on the real line and satisfies 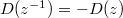 .
.
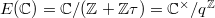 , with
, with 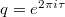 . Bloch defined the elliptic dilogarithm
. Bloch defined the elliptic dilogarithm 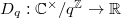 by averaging
by averaging 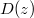 using the action of
using the action of 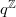 on
on 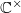 ,
, 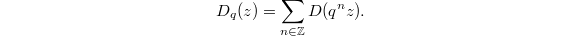
This is a purely complex analytic construction. Interesting things happen when evaluating 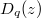 at rational points of
at rational points of 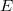 .
.
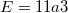 has complex uniformization
has complex uniformization 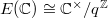 , where
, where 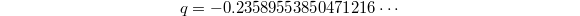 We have
We have 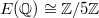 with
with 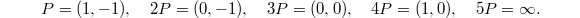 Under the complex uniformization,
Under the complex uniformization, 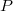 corresponds to
corresponds to 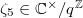 . We can compute
. We can compute 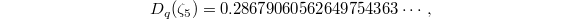 and
and 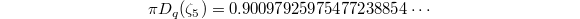 Now the miracle is
Now the miracle is 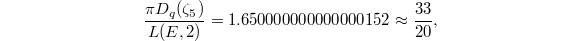 which looks like a rational number! In other words, we find a rational point
which looks like a rational number! In other words, we find a rational point 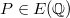 whose elliptic dilogarithm
whose elliptic dilogarithm 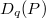 contributes the transcendental part of
contributes the transcendental part of 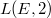 .
.
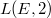 only depends on the
only depends on the 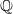 -isogeny class of
-isogeny class of 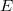 . What happens when we choose a different curve in the same isogeny class? Here is an example to illustrate the subtlety. Let
. What happens when we choose a different curve in the same isogeny class? Here is an example to illustrate the subtlety. Let 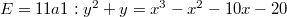 . It is 5-isogenous to
. It is 5-isogenous to 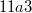 and thus has the same
and thus has the same 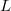 -function as
-function as 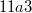 . It has complex uniformization
. It has complex uniformization 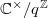 with
with 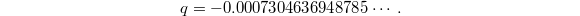 We also have
We also have 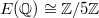 , with
, with 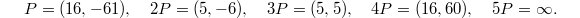 Again
Again 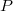 corresponds to
corresponds to 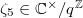 . We can compute
. We can compute 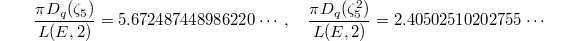 neither of which looks like a rational number. If we take the linear combination of these two transcendental numbers, the miracle happens again:
neither of which looks like a rational number. If we take the linear combination of these two transcendental numbers, the miracle happens again: 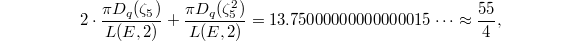 which should be rational! In other words we find the divisor
which should be rational! In other words we find the divisor ![$2[P]+ [2P]$](./latex/latex2png-BeilinsonBloch_249549800_-5.gif) supported on
supported on 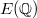 whose elliptic dilogarithm contributes to the transcendental part of
whose elliptic dilogarithm contributes to the transcendental part of 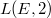 .
.
In general 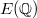 could be trivial and such a divisor supported on
could be trivial and such a divisor supported on 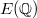 related to
related to 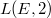 may not always exist. The next best thing one can hope:
may not always exist. The next best thing one can hope:
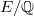 be an elliptic curve with
be an elliptic curve with 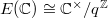 . There exists a
. There exists a 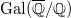 -stable divisor
-stable divisor 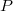 on
on 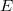 such that
such that 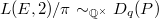 .
.
 K-Groups
K-Groups
We finish by explaining the role of algebraic 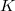 -theory in the proof. Algebraic
-theory in the proof. Algebraic 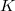 -theory is a sequence of functors
-theory is a sequence of functors 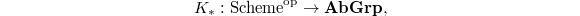 which, roughly speaking, extracts abelian invariants from "linear algebraic construction" over the scheme
which, roughly speaking, extracts abelian invariants from "linear algebraic construction" over the scheme 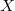 . For example,
. For example, 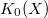 are abelian invariants of "vector spaces" over
are abelian invariants of "vector spaces" over 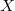 : it is the Grothendieck group on the isomorphism classes of vector bundles over
: it is the Grothendieck group on the isomorphism classes of vector bundles over 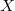 . Similarly,
. Similarly, 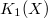 ,
, 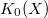 can be thought of as abelian invariants coming from "matrices" over
can be thought of as abelian invariants coming from "matrices" over 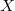 and "relations" between elementary matrices.
and "relations" between elementary matrices.
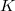 -groups simply because Grothendieck used the letter
-groups simply because Grothendieck used the letter 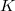 to denote his group (now we see the first connection between the two words in the title). Though this time the name had a bit justification:
to denote his group (now we see the first connection between the two words in the title). Though this time the name had a bit justification: 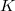 was intended to stand for the German word Klasse.
was intended to stand for the German word Klasse.
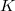 , we have
, we have 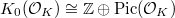 ,
, 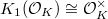 . So the invariants appearing in Dirichlet's theorem can all be rephrased in terms of pieces of these
. So the invariants appearing in Dirichlet's theorem can all be rephrased in terms of pieces of these 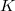 -groups. In particular, we can interpret the regulator as the determinant of the regulator map
-groups. In particular, we can interpret the regulator as the determinant of the regulator map 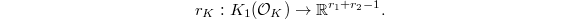
The generalization for the logarithm we seek now can be thought as a regulator map 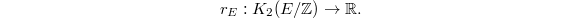 To construct
To construct 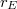 we need to understand what
we need to understand what 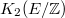 is. Unfortunately Quillen's
is. Unfortunately Quillen's 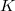 -group are highly nonconstructive and are very difficult to compute. We do not explain Quillen's construction here since we will not need it. The key fact we will use is that for a field
-group are highly nonconstructive and are very difficult to compute. We do not explain Quillen's construction here since we will not need it. The key fact we will use is that for a field 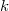 ,
, 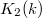 can be identified as Milnor's
can be identified as Milnor's 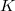 -group (defined for fields)
-group (defined for fields) 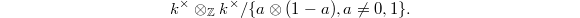 This explains the following construction and the importance of the function
This explains the following construction and the importance of the function 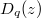 .
.
Thus 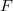 descends to a map
descends to a map 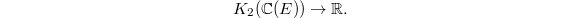 Now composing the functorial map, we obtain Bloch's regulator map
Now composing the functorial map, we obtain Bloch's regulator map 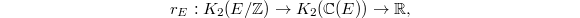 where
where 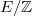 denotes the Neron model of
denotes the Neron model of 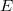 over
over 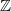 .
.
This is quite elegant but the difficulty dramatically increases compared to Dirichlet's theorem. For example it is not even known that 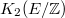 is finitely generated! Notice, for a field
is finitely generated! Notice, for a field 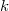 , by the localization exact sequence,
, by the localization exact sequence, 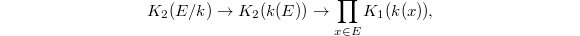 the elements in
the elements in 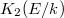 can be represented by elements of the form
can be represented by elements of the form 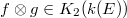 which maps trivially into
which maps trivially into 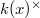 for each point
for each point 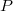 . What Bloch and Beilinson did is something weaker than the conjecture: they were able to construct explicit elements (represented as above) in
. What Bloch and Beilinson did is something weaker than the conjecture: they were able to construct explicit elements (represented as above) in 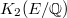 and relate their regulators to
and relate their regulators to 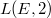 . In other words, they prove that there is a subspace of
. In other words, they prove that there is a subspace of 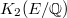 whose image under
whose image under 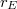 is a rational multiple of
is a rational multiple of 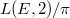 .
.
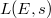 is a Hecke
is a Hecke 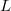 -series and Bloch's evaluation of the regulator map at functions supported at torsion points mimics the classical computation of Kummer relating Dirichlet
-series and Bloch's evaluation of the regulator map at functions supported at torsion points mimics the classical computation of Kummer relating Dirichlet 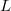 -series and logarithm of cyclotomic units, via Fourier transform. For the general case, Beilinson used another construction of the regulator map, which replaces the target
-series and logarithm of cyclotomic units, via Fourier transform. For the general case, Beilinson used another construction of the regulator map, which replaces the target 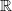 by the Deligne cohomology group
by the Deligne cohomology group  (which is one dimensional). To be more precise, Beilinson works with modular curves and the value of the regulator map at a modular unit gives an integral of the product of
(which is one dimensional). To be more precise, Beilinson works with modular curves and the value of the regulator map at a modular unit gives an integral of the product of 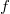 and two Eisenstein series, which evaluates to
and two Eisenstein series, which evaluates to 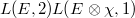 for some Dirichlet characters
for some Dirichlet characters 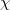 , via Rankin's method.
, via Rankin's method.
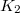 of modular curves constructed by Beilinson were later used by Kato to construct Euler systems and became the starting point of Kato's proof [8] of the BSD conjecture in the analytic rank zero case and one divisibility in the Iwasawa main conjecture for
of modular curves constructed by Beilinson were later used by Kato to construct Euler systems and became the starting point of Kato's proof [8] of the BSD conjecture in the analytic rank zero case and one divisibility in the Iwasawa main conjecture for 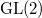 .
.
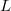 -functions by constructing regulator maps from motivic cohomology to Deligne cohomolgy, which is further generalized in the framework of mixed motives. For the list of (very few) proved cases, see the end of [9].
-functions by constructing regulator maps from motivic cohomology to Deligne cohomolgy, which is further generalized in the framework of mixed motives. For the list of (very few) proved cases, see the end of [9].
References
[1]Algebraic $K$-theory and zeta functions of elliptic curves, Proceedings of the International Congress of Mathematicians (Helsinki, 1978), Acad. Sci. Fennica, Helsinki, 1980, 511--515.
[2]$K_2$ and $L$-functions of elliptic curves: computer calculations, Applications of algebraic $K$-theory to algebraic geometry and number theory, Part I, II (Boulder, Colo., 1983), Contemp. Math., 55 Amer. Math. Soc., Providence, RI, 1986, 79--88.
[3]Higher regulators, algebraic $K$-theory, and zeta functions of elliptic curves, American Mathematical Society, Providence, RI, 2000.
[4]Classical and elliptic polylogarithms and special values of $L$-series, The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), NATO Sci. Ser. C Math. Phys. Sci., 548 Kluwer Acad. Publ., Dordrecht, 2000, 561--615.
[5]Zagier's conjecture on $L(E,2)$, Invent. Math. 132 (1998), no.2, 393--432.
[6]Zagier's conjectures on special values of $L$-functions, Riv. Mat. Univ. Parma (7) 3* (2004), 165--176.
[7]Higher regulators of modular curves, Applications of algebraic $K$-theory to algebraic geometry and number theory, Part I, II (Boulder, Colo., 1983), Contemp. Math., 55 Amer. Math. Soc., Providence, RI, 1986, 1--34.
[8]$p$-adic Hodge theory and values of zeta functions of modular forms, Astérisque (2004), no.295, ix, 117--290.
[9]Be\u\i linson's conjectures, Motives (Seattle, WA, 1991), Proc. Sympos. Pure Math., 55 Amer. Math. Soc., Providence, RI, 1994, 537--570.
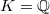 , we have
, we have 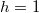 ,
, 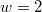 ,
, 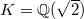 , we have
, we have ![$\mathcal{O}_K=\mathbb{Z}[\sqrt{2}]$](./latex/latex2png-BeilinsonBloch_254690350_-5.gif) ,
, 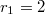 ,
, 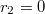 ,
, 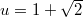 ,
, 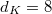 . So
. So 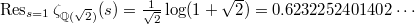 .
.
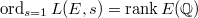 .
.
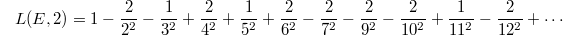 Numerically one can compute that
Numerically one can compute that 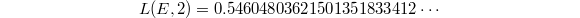
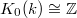 ,
, 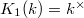 .
.
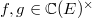 with divisor
with divisor 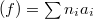 ,
, 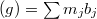 . Define
. Define 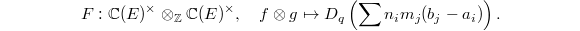 Then
Then 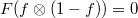 for any
for any