The tilting functor induces an equivalence between the category of finite extensions of a perfectoid field 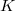 and the category of finite extensions of its tilt
and the category of finite extensions of its tilt 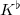 . The proof of this fact (and further generalization in families) relies on Faltings' almost mathematics. We shall introduce the necessary background in almost ring theory and sketch the proof following Chapter 4 of Scholze's paper [1].
. The proof of this fact (and further generalization in families) relies on Faltings' almost mathematics. We shall introduce the necessary background in almost ring theory and sketch the proof following Chapter 4 of Scholze's paper [1].
This is an expanded note prepared for a STAGE talk at MIT, Fall 2013. Our main references are [1] and [2]. I would like to thank George Boxer for helpful discussions.
 Motivation
Motivation
Recall that a perfectoid field 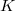 is a complete nonarchimedean field of residue field of characteristic
is a complete nonarchimedean field of residue field of characteristic 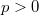 such that
such that
- The valuation is nondiscrete of rank 1.
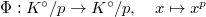 is surjective.
is surjective.
We also defined a tilting operation: let 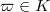 such that
such that 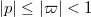 . Then
. Then ![$$K^{\flat}=(\varprojlim_{\Phi} K^\circ/\varpi)[(\varpi^{\flat})^{-1}],$$](./latex/latex2png-AlmostMathematics_3882529_.gif) where
where 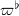 is an element of
is an element of 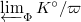 such that
such that 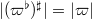 . We have
. We have 
The following is the main theorem of today's talk, which already appeared in the classical work of Fontaine-Wintenberger [3] for many fields.
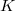 be a perfectoid field. The the tilting functor
be a perfectoid field. The the tilting functor 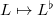 induces an equivalence between of the category of finite extensions of
induces an equivalence between of the category of finite extensions of 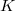 and the category of finite extensions of
and the category of finite extensions of 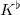 .
.
In particular, one obtains a canonical isomorphism between the absolute Galois group of (a characteristic 0 field) 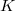 and the absolute Galois group of (a characteristic
and the absolute Galois group of (a characteristic 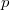 field)
field) 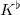 . To convince you that this is really a miracle, let us consider the following two (non-)examples.
. To convince you that this is really a miracle, let us consider the following two (non-)examples.
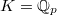 satisfies the condition b) but not a) in the definition of perfectoid fields. If one has the gut to compute the tilt of
satisfies the condition b) but not a) in the definition of perfectoid fields. If one has the gut to compute the tilt of 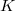 anyway, one easily finds that
anyway, one easily finds that 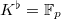 .
.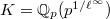 satisfies the condition a) but not b) and one finds that
satisfies the condition a) but not b) and one finds that 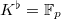 too.
too.
In both cases, one loses tons of information when passing to the tilt and the above main theorem is far from true!
So how does one prove such a miraculous theorem? The main tool is Faltings' almost mathematics. Let us look at the following simple example to motivate this idea.
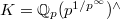 be a perfectoid field. Assume
be a perfectoid field. Assume 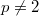 , then
, then 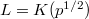 is a degree 2 extension of
is a degree 2 extension of 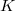 . The key observation is that though
. The key observation is that though 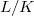 is certainly ramified, it is almost unramified. Consider the extension at the finite level
is certainly ramified, it is almost unramified. Consider the extension at the finite level 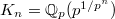 and
and 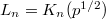 . Then by Bezout,
. Then by Bezout, 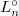 is generated over
is generated over 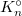 by
by 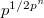 . One computes the relative different
. One computes the relative different 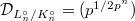 , whose (additive) valuation tends to 0 when
, whose (additive) valuation tends to 0 when 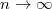 . Namely, the ramification gets arbitrarily small when
. Namely, the ramification gets arbitrarily small when 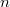 gets arbitrarily large! Another way to say this is that the module of Kahler differentials
gets arbitrarily large! Another way to say this is that the module of Kahler differentials 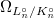 is killed by
is killed by 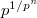 for arbitrarily large
for arbitrarily large 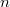 , i.e., killed by arbitrarily small power of
, i.e., killed by arbitrarily small power of 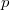 (= killed by the maximal ideal
(= killed by the maximal ideal 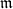 of
of 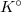 ).
).
So we would like to consider a category of 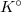 -modules where the
-modules where the 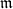 -torsion are systematically ignored ( almost
-torsion are systematically ignored ( almost 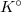 -modules, or
-modules, or 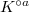 -modules) and use this category to define the notion of almost finite etale
-modules) and use this category to define the notion of almost finite etale 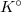 -algebra rigorously.
-algebra rigorously. ![$$\xymatrix{ K^\circ\Mod \ar[rr]^{\text{ignoring all $p$-power torsion}} \ar[rd]_{\text{ignoring only}\atop\text{small $p$-power torsion}} & & K\Mod & \text{(generic fiber)}\\ & K^{\circ a}\Mod \ar[ru] & &\text{(slightly generic fiber)} }$$](./latex/latex2png-AlmostMathematics_4026790_.gif) In view of the above example, a finite (= finite etale) extension
In view of the above example, a finite (= finite etale) extension 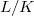 is expected to extend automatically to an almost finite etale extension
is expected to extend automatically to an almost finite etale extension 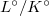 on the integral level. This is known as almost purity (analogous to the Nagata-Zariski's purity theorem on the branch locus in algebraic geometry) and lies in the core of the proof of the above stated main theorem.
on the integral level. This is known as almost purity (analogous to the Nagata-Zariski's purity theorem on the branch locus in algebraic geometry) and lies in the core of the proof of the above stated main theorem.
 Almost modules and almost algebras
Almost modules and almost algebras
Fix a perfectoid field 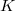 with valuation ring
with valuation ring 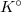 and maximal ideal
and maximal ideal 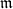 .
.
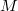 be a
be a 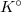 -module. We say
-module. We say 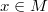 is almost zero if
is almost zero if 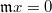 . We say
. We say 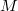 is almost zero if every element of
is almost zero if every element of 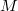 is almost zero, i.e.,
is almost zero, i.e., 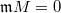 .
.
We would like to "quotient out" all almost zero modules. We recall the machinery to do so: the quotient of an abelian category by a Serre subcategory.
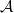 be an abelian category. A Serre subcategory is a full subcategory
be an abelian category. A Serre subcategory is a full subcategory 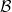 of
of 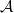 such that for any exact sequence
such that for any exact sequence 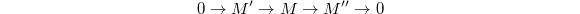 in
in 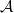 , one has
, one has 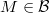 if and only if
if and only if 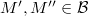 . Suppose
. Suppose 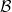 is a Serre subcategory, the one can form the quotient category
is a Serre subcategory, the one can form the quotient category 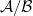 , whose objects are the objects of
, whose objects are the objects of 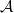 , and for
, and for 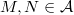 ,
, 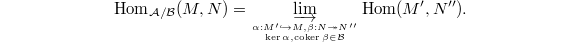 The quotient category is again an abelian category. By construction, one has a canonical localization functor
The quotient category is again an abelian category. By construction, one has a canonical localization functor 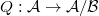 . If
. If 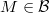 , then
, then 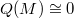 in
in 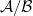 . The quotient category enjoys the following universal property: suppose
. The quotient category enjoys the following universal property: suppose 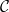 is another abelian category and
is another abelian category and 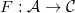 is an exact functor such that
is an exact functor such that 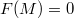 for any
for any 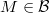 , then
, then 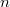 uniquely facts through
uniquely facts through 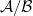 .
.
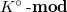 consisting of almost zero
consisting of almost zero 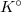 -modules is a Serre subcategory of
-modules is a Serre subcategory of 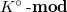 . Denote the quotient category by
. Denote the quotient category by 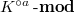 .
.
 is
is  -torsion, then clearly any sub or quotient of
-torsion, then clearly any sub or quotient of 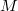 is also
is also 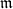 -torsion. Conversely, if
-torsion. Conversely, if 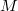 is an extension of
is an extension of 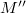 by
by 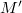 , where
, where 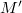 and
and 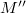 are
are 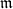 -torsion, then
-torsion, then 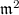 kills
kills 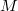 . But the valuation on
. But the valuation on 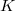 is nondiscrete, we have
is nondiscrete, we have 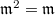 .
¡õ
.
¡õ
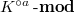 is called the category of almost
is called the category of almost 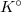 -modules, or
-modules, or 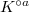 -modules. For
-modules. For 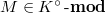 , we denote
, we denote 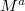 to be its image under the localizing functor, i.e., the same object viewed in the almost category
to be its image under the localizing functor, i.e., the same object viewed in the almost category 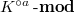 .
.
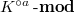 has all formal properties of the category of modules over a commutative ring. So one can define the notion of almost
has all formal properties of the category of modules over a commutative ring. So one can define the notion of almost 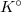 -algebras, or
-algebras, or 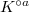 -algebras: these are commutative unitary monoid objects in
-algebras: these are commutative unitary monoid objects in 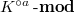 . Let
. Let 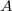 be a
be a 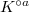 -algebra, one can also define the notation of
-algebra, one can also define the notation of 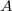 -modules and
-modules and 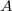 -algebras. I should stop boring you by defining them and refer you to the details in [2, 2.2.5]. Just to mention that, for example, an
-algebras. I should stop boring you by defining them and refer you to the details in [2, 2.2.5]. Just to mention that, for example, an 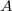 -algebra is an object
-algebra is an object 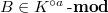 together with an almost morphism
together with an almost morphism 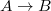 .
.
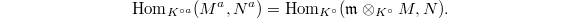 This is a
This is a 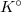 -module (an honest module!) with no almost zero elements. We define
-module (an honest module!) with no almost zero elements. We define 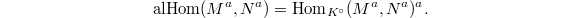
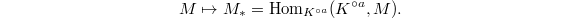 One easily checks (by the previous remark) that
One easily checks (by the previous remark) that 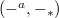 is an adjoint pair and
is an adjoint pair and 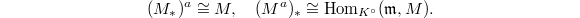
 Almost properties
Almost properties
 be a
be a 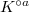 -algebra and
-algebra and 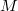 be an
be an 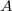 -module.
-module.
- We say
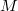 is flat if the functor
is flat if the functor 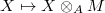 is flat on
is flat on 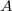 -modules.
-modules. - We say
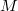 is almost projective if the functor
is almost projective if the functor 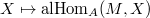 is exact on
is exact on 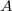 -modules. (There is the usual notion of projectivity, but it turns out to be ill-behaved: even
-modules. (There is the usual notion of projectivity, but it turns out to be ill-behaved: even 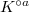 is not projective over itself.)
is not projective over itself.) - Let
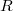 be a
be a 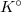 -algebra and
-algebra and 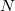 be an
be an 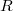 -module such that
-module such that 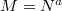 and
and 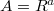 . We say
. We say 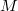 is almost finitely generated if for all
is almost finitely generated if for all 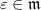 , there is some finitely generated
, there is some finitely generated 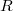 -module
-module 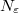 together with a map
together with a map 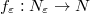 such that
such that 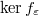 and
and 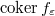 are killed by
are killed by  . We further say that
. We further say that 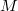 is uniformly finitely generated if there exists some integer
is uniformly finitely generated if there exists some integer 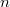 , such that
, such that 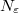 can be generated by
can be generated by 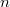 elements for all
elements for all  . These notions do not depend on the choice of
. These notions do not depend on the choice of 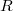 and
and 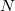 .
. - We similarly define the notion of almost finitely presented modules.
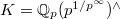 and
and 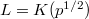 (
(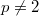 ). Notice
). Notice 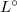 is not finitely generated as a
is not finitely generated as a 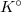 -module: one needs the generators
-module: one needs the generators 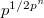 for arbitrarily large
for arbitrarily large 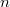 . But
. But 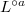 is an almost finitely generated as a
is an almost finitely generated as a 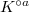 -module. Indeed, for any
-module. Indeed, for any 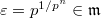 , the inclusion
, the inclusion 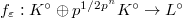 has cokernel which is killed by
has cokernel which is killed by  . We also see that
. We also see that 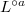 is almost finitely presented and uniformly finitely generated (
is almost finitely presented and uniformly finitely generated (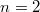 ) as a
) as a 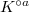 -module.
-module.
Finally, we can define the notion of almost finite etale algebras.
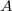 be a
be a 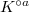 -algebra and
-algebra and 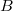 be an
be an 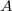 -algebra.
-algebra.
- We say
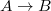 is unramified if there is some element
is unramified if there is some element 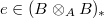 such that
such that 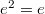 ,
, 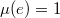 and
and 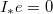 , where
, where 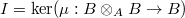 and
and 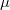 is the multiplication morphism.
is the multiplication morphism. - We say
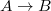 is etale if it is unramified and
is etale if it is unramified and 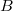 is flat as an
is flat as an 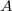 -module.
-module. - We say
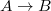 is finite etale if it is etale and
is finite etale if it is etale and 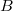 is almost finitely presented as an
is almost finitely presented as an 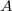 -module. Denote by
-module. Denote by 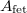 the category of finite etale
the category of finite etale 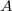 -algebras.
-algebras.
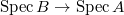 of finite type is unramified if and only if the diagonal morphism
of finite type is unramified if and only if the diagonal morphism 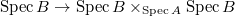 is an open and closed immersion. So one can think of
is an open and closed immersion. So one can think of 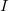 as functions vanishing on the diagonal and
as functions vanishing on the diagonal and  as the characteristic function on the diagonal.
as the characteristic function on the diagonal.
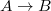 is unramified is equivalent to saying that
is unramified is equivalent to saying that 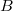 is almost projective as a
is almost projective as a 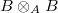 -module under
-module under 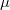 ; also equivalent to saying that
; also equivalent to saying that 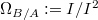 vanishes in the almost category.
vanishes in the almost category.
 Almost a sketch of the proof
Almost a sketch of the proof
The following diagram illustrates the structure of the proof of the main theorem. We would like to show that all the arrows in the diagram are equivalences. ![$$\xymatrix{K_{\mathrm{fet}} & K^{\circ a}_{\mathrm{fet}} \ar[r]^-{(2)} \ar[l]_-{(1)} & (K^{\circ a}/\varpi)_{\mathrm{fet}} \ar@{=}[d] \\ K^{\flat}_{\mathrm{fet}} & K^{\flat \circ a}_{\mathrm{fet}} \ar[r]^-{(3)} \ar[l]_-{(4)} & (K^{\flat \circ a}/\varpi^{\flat})_{\mathrm{fet}}}$$](./latex/latex2png-AlmostMathematics_208360065_.gif) Here the left arrow (1) is the generic fiber functor
Here the left arrow (1) is the generic fiber functor ![$A\mapsto A_*[\varpi^{-1}]$](./latex/latex2png-AlmostMathematics_72763866_-5.gif) and the right arrow (2) is the reduction functor
and the right arrow (2) is the reduction functor 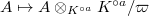 . The arrows (3) and (4) are similarly defined.
. The arrows (3) and (4) are similarly defined.
Step 1 Show (2) and (3) are equivalences. This boils down to prove that any finite etale algebras lift uniquely over nilpotents. This is not so surprising and is true in much more generality:
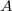 be an
be an 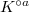 -algebra. Suppose
-algebra. Suppose 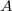 is flat as an
is flat as an 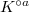 -module and
-module and 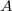 is
is 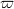 -adically complete. Then the reduction functor
-adically complete. Then the reduction functor 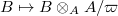 is an equivalence of between the categories
is an equivalence of between the categories 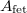 and
and 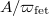 .
.
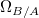 in the almost category). Taking
in the almost category). Taking 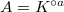 or
or 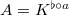 gives the desired equivalences (2) and (3).
gives the desired equivalences (2) and (3).
Step 2 Show (1) and (4) are fully faithful. This can be checked directly and is also a consequence of the (easy) equivalence between the larger categories of perfectoid algebras over 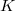 and
and 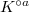 . In particular, the essential image of (1) consists of finite etale algebras
. In particular, the essential image of (1) consists of finite etale algebras 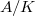 such that
such that 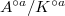 is finite etale. To show the equivalence (1) and (4), it suffices to show that
is finite etale. To show the equivalence (1) and (4), it suffices to show that
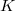 be a perfectoid field. If
be a perfectoid field. If 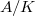 is a finite etale algebra, then
is a finite etale algebra, then 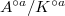 is finite etale.
is finite etale.
Step 3 Show the almost purity for perfectoid fields 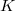 of characteristic
of characteristic 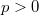 (hence (4) is an equivalence). This is not difficult by the existence of Frobenius. Here is the outline of the argument. Suppose
(hence (4) is an equivalence). This is not difficult by the existence of Frobenius. Here is the outline of the argument. Suppose 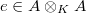 is the idempotent from the finite etale algebra
is the idempotent from the finite etale algebra 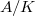 , then there exists some integer
, then there exists some integer 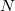 such that
such that 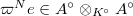 . Since the Frobenius is surjective,
. Since the Frobenius is surjective, 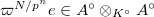 as well for any
as well for any 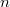 . Since
. Since 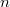 can be arbitrarily large, we obtain an almost idempotent for
can be arbitrarily large, we obtain an almost idempotent for 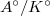 as desired.
as desired.
Step 4 Show the almost purity for perfectoid fields 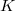 of characteristic 0 (hence (1) is an equivalence). This is very difficult. One can find a proof in [2, 6.6.6] using ramification theory (alluded in the beginning of this talk) . Over more general base, the almost purity is proved by Faltings in [4]. Scholze's theory of perfectoid spaces gives a new proof of this hard theorem.
of characteristic 0 (hence (1) is an equivalence). This is very difficult. One can find a proof in [2, 6.6.6] using ramification theory (alluded in the beginning of this talk) . Over more general base, the almost purity is proved by Faltings in [4]. Scholze's theory of perfectoid spaces gives a new proof of this hard theorem.
References
[1]Perfectoid spaces, ArXiv e-prints (2011).
[2]Almost ring theory - sixth release, ArXiv Mathematics e-prints (2002).
[3]Le ``corps des normes'' de certaines extensions algébriques de corps locaux, C. R. Acad. Sci. Paris Sér. A-B 288 (1979), no.6, A367--A370.
[4]Almost étale extensions, Astérisque (2002), no.279, 185--270.
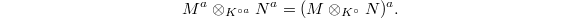 It is a well-defined on
It is a well-defined on  an abelian tensor category.
an abelian tensor category.