These are my live-TeXed notes for the course Math G6659: Langlands correspondence for general reductive groups over function fields taught by Michael Harris at Columbia, Spring 2016.
Any mistakes are the fault of the notetaker. Let me know if you notice any mistakes or have any comments!
01/26/2016
 Introduction
Introduction
This course will discuss one of the most exciting recent development in automorphic forms and number theory: the paper (still under revision) Chtoucas pour les groupes reductifs et parametrisation de Langlands globale of Vincent Lafforgue on the global Langlands correspondence over function fields. I have been thinking about his paper for a few years and more intensively in the past several months. The more I think about it the more I realize that my original intention was unrealistic due to the huge amount of technical material. I was trying the write up the notes for each lecture during the break, but every single day (at least 80 percent of the time) I realised the topic I was tring to discuss could well be a semester course in itself. To be more realistic, I will not try to explain the entire proof but rather to explain the background, present the framework of the Langlands correspondence and explain some highlights of the proof in details. We will also have five extra sessions on background of Langlands correspondence: including 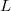 -groups, the Satake isomorphism and representations of adelic groups and so on (the notetaker will not attend these due to scheduling conflicts but refers to his other notes for the background.)
-groups, the Satake isomorphism and representations of adelic groups and so on (the notetaker will not attend these due to scheduling conflicts but refers to his other notes for the background.)
Let us begin with the standard function field set-up. Let 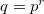 be a prime power and
be a prime power and 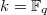 . Let
. Let 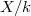 be a smooth irreducible projective curve and
be a smooth irreducible projective curve and 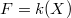 its field of rational functions. Recall that the valuations on
its field of rational functions. Recall that the valuations on 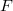 corresponds bijectively to closed points of
corresponds bijectively to closed points of  over finite extensions of
over finite extensions of 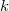 . Let
. Let  a valuation of
a valuation of 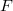 and
and 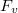 be its completion. If
be its completion. If  is the residue field, then
is the residue field, then 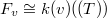 , with its ring of integers
, with its ring of integers ![$\mathcal{O}_v\cong k(v)[ [T] ]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_105946975_-5.gif) . Notice there is only one kind of localization in the function field case, which simplifies things a bit (but not too much) compared to the number field case.
. Notice there is only one kind of localization in the function field case, which simplifies things a bit (but not too much) compared to the number field case.
Let  be a connected reductive group over
be a connected reductive group over 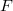 . For simplicity we assume
. For simplicity we assume  is coming from base extension from a split group over
is coming from base extension from a split group over 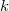 . We almost always assume
. We almost always assume  is semisimple (e.g.,
is semisimple (e.g., 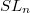 ,
, 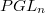 ,
, 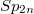 ,
, 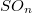 ,
, 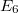 ,
, 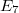 ,
, 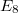 ,
, 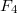 ,
, 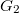 ), or otherwise
), or otherwise 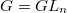 . Notice V. Lafforgue works in much more generality.
. Notice V. Lafforgue works in much more generality.
Recall that 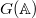 is the restricted product
is the restricted product 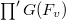 with respect to
with respect to 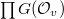 . Let
. Let 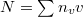 be an effective divisor on
be an effective divisor on  . Let
. Let 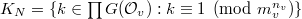 be the open compact subgroup of level
be the open compact subgroup of level 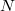 . Let
. Let 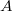 be a coefficient ring (usually
be a coefficient ring (usually 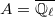 ,
, 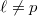 , sometimes
, sometimes 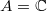 ). Recall:
). Recall:
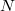 with coefficient in
with coefficient in 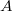
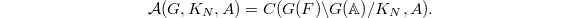 Notice these automorphic forms are automatically locally constant. The space
Notice these automorphic forms are automatically locally constant. The space 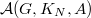 is the fixed space
is the fixed space 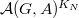 of the space of all automorphic forms
of the space of all automorphic forms 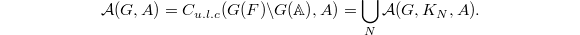 Here the subscript means uniformly locally constant functions.
Here the subscript means uniformly locally constant functions.
 (or
(or  is not semisimple), we choose a discrete subgroup
is not semisimple), we choose a discrete subgroup  in the center so that
in the center so that 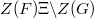 is compact. All I am about to say will be true after this modification.
is compact. All I am about to say will be true after this modification.
The adelic group 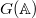 acts on
acts on 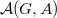 by right translation. The central question in the theory of automorphic forms is to decompose this space as
by right translation. The central question in the theory of automorphic forms is to decompose this space as 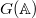 -representations.
-representations.
Let 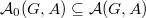 be the space of cusp forms. If
be the space of cusp forms. If 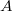 is algebraically closed, then we have a decomposition
is algebraically closed, then we have a decomposition 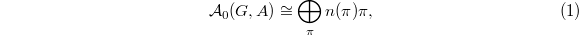 where
where 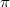 runs through (a countable set of) admissible irreducible representations of
runs through (a countable set of) admissible irreducible representations of 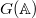 and
and 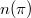 is a non-negative integer. The central question is to determine the multiplicity
is a non-negative integer. The central question is to determine the multiplicity 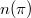 for any
for any 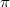 . In particular, to determine which abstract representations
. In particular, to determine which abstract representations 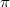 are automorphic (i.e.
are automorphic (i.e. 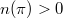 ). Fix
). Fix 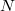 , the question becomes to determine
, the question becomes to determine 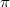 with
with 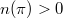 and
and 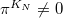 . The conjectural answer is provided by Langlands parameters:
. The conjectural answer is provided by Langlands parameters:
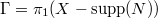 be the Galois group of the maximal separable extension of
be the Galois group of the maximal separable extension of 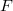 unramified outside the support of
unramified outside the support of 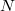 . A Langlands parameter (unramified outside
. A Langlands parameter (unramified outside 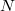 ) is a homomorphism
) is a homomorphism 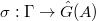 , up to conjugacy by
, up to conjugacy by 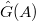 , where
, where 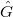 is the Langlands dual group of
is the Langlands dual group of  .
.
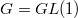 , the conjecture boils down to class field theory. When
, the conjecture boils down to class field theory. When 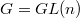 , Laurent Lafforgue proved the conjecture and in this case the multiplicity of automorphic representations is always 1.
, Laurent Lafforgue proved the conjecture and in this case the multiplicity of automorphic representations is always 1.
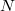 . This is the Galois group
. This is the Galois group 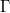 , at least after taking the
, at least after taking the  -adic realization: the independence of
-adic realization: the independence of  for the Langlands parameters is still an issue.
for the Langlands parameters is still an issue.
The beginning of V. Lafforgue's theorem is:
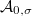 is a sum of
is a sum of 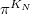 , i.e. this decomposition is an refinement of the decomposition (1).
, i.e. this decomposition is an refinement of the decomposition (1).
Recall that the decomposition of 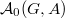 is given by the action of the Hecke algebra
is given by the action of the Hecke algebra 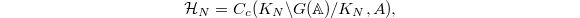 which is an algebra under convolution with identity
which is an algebra under convolution with identity 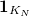 . The Hecke algebra
. The Hecke algebra 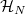 acts on
acts on 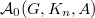 by convolution operators: for
by convolution operators: for 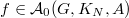 ,
, 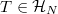 ,
, 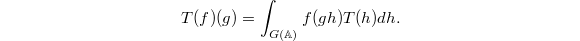 The Hecke algebra decomposes as restricted product of local Hecke algebras
The Hecke algebra decomposes as restricted product of local Hecke algebras 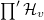 . The basic fact is that
. The basic fact is that
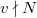 , then
, then
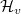 is a commutative algebra over
is a commutative algebra over 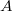 , isomorphic to a polynomial algebra.
, isomorphic to a polynomial algebra.- There is a canonical bijection between the characters
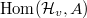 with semisimple conjugacy classes in
with semisimple conjugacy classes in 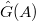 .
.
It follows that 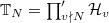 is a commutative algebra and acts on
is a commutative algebra and acts on 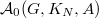 and decomposes it into a direct sum over
and decomposes it into a direct sum over 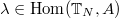 . Each
. Each 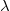 gives a collection of semisimple conjugacy classes
gives a collection of semisimple conjugacy classes 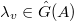 indexed by
indexed by 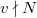 .
.
V. Lafforgue defines a new commutative algebra 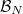 of excursion operators acting on
of excursion operators acting on 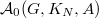 . It contains the image of
. It contains the image of 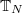 and moreover connects to Galois representations: any Langlands parameter
and moreover connects to Galois representations: any Langlands parameter 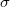 is in fact a character of
is in fact a character of 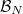 !
!
More precisely, for any 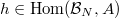 , V. Lafforgue associates a Langlands parameter
, V. Lafforgue associates a Langlands parameter 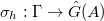 . When
. When 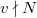 ,
, 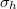 is unramified at
is unramified at  and hence defines a conjugacy class
and hence defines a conjugacy class 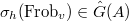 . The crucial property of the decomposition in Theorem 1 is
. The crucial property of the decomposition in Theorem 1 is
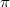 a globally generic automorphic representation, let
a globally generic automorphic representation, let 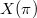 be the subset of
be the subset of 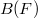 -orbits of generic characters that
-orbits of generic characters that 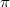 is generic with respect to. If
is generic with respect to. If 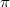 and
and 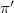 are locally isomorphic everywhere but not globally, then the conjecture is that
are locally isomorphic everywhere but not globally, then the conjecture is that 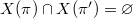 . The different way to extend from the Hecke algebra to the excursion algebra should be indexed by these subsets of generic characters. When
. The different way to extend from the Hecke algebra to the excursion algebra should be indexed by these subsets of generic characters. When  is adjoint, one can compute that the set of generic character is a singleton and therefore the image of the Hecke algebra and the (semi-simplification of ) the excursion algebra should be the same.
is adjoint, one can compute that the set of generic character is a singleton and therefore the image of the Hecke algebra and the (semi-simplification of ) the excursion algebra should be the same.
Blasius (for 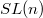 ) and Larsen (for
) and Larsen (for 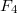 ) have constructed examples of generic automorphic representations (over number fields) which are locally isomorphic but not globally. For
) have constructed examples of generic automorphic representations (over number fields) which are locally isomorphic but not globally. For 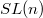 there are
there are 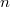 orbits of generic characters and these automorphic representations can be distinguished by these different orbits. But for
orbits of generic characters and these automorphic representations can be distinguished by these different orbits. But for 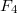 (adjoint), there is only one orbit of generic characters and such examples of generic automorphic representations are unramified everywhere. The Whittaker functional
(adjoint), there is only one orbit of generic characters and such examples of generic automorphic representations are unramified everywhere. The Whittaker functional 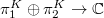 is nonzero on both factors and has 1-dimensional kernel. They can be detected by the global parameter (the character of the Hecke algebra extends to the excursion algebra in different ways). Question: can they be distinguished in a purely automorphic way (e.g., by non-Whittaker type of Fourier coefficients?)
is nonzero on both factors and has 1-dimensional kernel. They can be detected by the global parameter (the character of the Hecke algebra extends to the excursion algebra in different ways). Question: can they be distinguished in a purely automorphic way (e.g., by non-Whittaker type of Fourier coefficients?)
01/28/2016
Today we will introduce the objects which V. Lafforgue uses to construct the global Langlands parameter. One novelty of his work is that he does not construct the global parameter directly but instead he constructs some combinatorial invariant involving the Galois group and 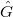 . He then uses geometric invariant theory to show that the combinatorial invariant is equivalent to a global parameter.
. He then uses geometric invariant theory to show that the combinatorial invariant is equivalent to a global parameter.
 and an algebraic dimensional representation
and an algebraic dimensional representation 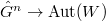 , where
, where 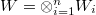 , V. Lafforgue, following Varshavsky, associates a moduli stack
, V. Lafforgue, following Varshavsky, associates a moduli stack 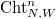 , the moduli stack of
, the moduli stack of  -shtukas of level
-shtukas of level 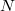 and paws (or legs) bounded by
and paws (or legs) bounded by 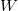 . It is a Deligne-Mumford (ind-)stack, hence can be thought of as a finite quotient of a scheme locally. For a test scheme
. It is a Deligne-Mumford (ind-)stack, hence can be thought of as a finite quotient of a scheme locally. For a test scheme 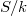 ,
, 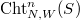 classifies the following data:
classifies the following data:
- An
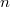 -tuple
-tuple 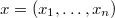 of
of  -points on
-points on  .
. - A
 -torsor
-torsor 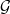 over
over 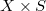 .
. - An isomorphism
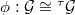 away from the union of the graphs of
away from the union of the graphs of 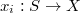 , where
, where 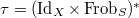 , such that the relative position of
, such that the relative position of 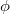 at each
at each 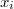 is bounded by the dominant weight of
is bounded by the dominant weight of 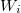 (a coweight of
(a coweight of  ).
). - A trivialization of
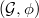 along
along 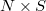 , i.e., an isomorphism
, i.e., an isomorphism 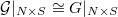 .
.
 -torsor as a functor
-torsor as a functor 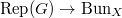 . When
. When 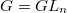 , this is the same as a vector bundle of rank
, this is the same as a vector bundle of rank 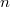 . For general
. For general  , this may be thought of as a vector bundle with extra structures.
, this may be thought of as a vector bundle with extra structures.
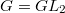 ,
, 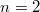 ,
, 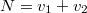 consists of two points,
consists of two points, 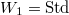 and
and 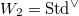 , a point of
, a point of 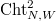 is exactly a Drinfeld shtukas with two legs with minuscule modification (a simple pole at
is exactly a Drinfeld shtukas with two legs with minuscule modification (a simple pole at 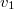 and a simple zero at
and a simple zero at 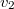 ).
).
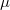 (dominant coweight of
(dominant coweight of  ) on the Harder-Narasimhan polygon gives an open substack
) on the Harder-Narasimhan polygon gives an open substack 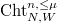 of finite type, which is in fact represented by a scheme when
of finite type, which is in fact represented by a scheme when 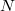 is sufficiently large.
is sufficiently large.
 -shtukas to its paws defines a paw morphism
-shtukas to its paws defines a paw morphism 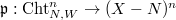 . We define a sheaf on
. We define a sheaf on 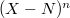 ,
, 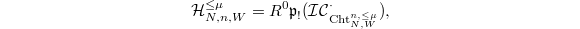 whose stalks should be thought of as the middle intersection cohomology with compact support.
whose stalks should be thought of as the middle intersection cohomology with compact support.
- When
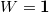 is the trivial representation,
is the trivial representation, 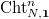 is the constant discrete stack
is the constant discrete stack 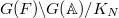 over
over 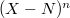 . It follows that
. It follows that 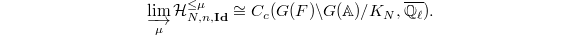
- The map
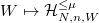 extends to an additive functor to
extends to an additive functor to 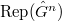 .
. - The stalk of
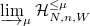 at a (good) geometric point contains the subspace
at a (good) geometric point contains the subspace 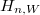 of Hecke finite elements.
of Hecke finite elements. - Each
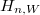 carries a monodromy action of
carries a monodromy action of 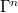 .
. - Given any morphism
![$\zeta: [m]\rightarrow [n]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_44436043_-5.gif) of finite sets of
of finite sets of 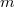 and
and 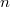 elements. There is a natural projection
elements. There is a natural projection ![$[\zeta]: \hat G^n\rightarrow \hat G^m$](./latex/VincentLafforgue/latex2png-VincentLafforgue_26151010_-5.gif) and similarly
and similarly ![$[\zeta]: \Gamma^n\rightarrow\Gamma^m$](./latex/VincentLafforgue/latex2png-VincentLafforgue_253670382_-5.gif) . For any
. For any 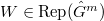 , composing with
, composing with ![$[\zeta]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_912088_-5.gif) defines
defines 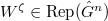 . There is a canonical isomorphism
. There is a canonical isomorphism 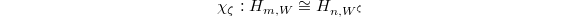 equivariant for the action of
equivariant for the action of 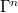 (which acts on the left hand side via
(which acts on the left hand side via ![$[\zeta]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_912088_-5.gif) ). Moreover,
). Moreover, 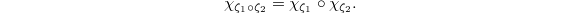 In fancier language, these data can be thought of as a morphism from the classifying stack of
In fancier language, these data can be thought of as a morphism from the classifying stack of 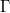 to the classifying stack of
to the classifying stack of 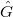 .
. - There is a canonical action of the Hecke algebra
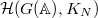 on each
on each 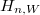 and all morphisms in (e) commute with this action.
and all morphisms in (e) commute with this action.
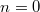 , the space
, the space 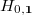 is known as the vacuum space, if one thinks of the paws as moving particles. The vacuum space has no Galois action but for larger
is known as the vacuum space, if one thinks of the paws as moving particles. The vacuum space has no Galois action but for larger 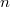 , the space
, the space 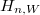 admits more and more Galois action. Drinfeld and L. Lafforgue computed
admits more and more Galois action. Drinfeld and L. Lafforgue computed 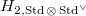 by comparing the Grothendieck-Lefschetz trace formula and Arthur-Selberg trace formula. V. Lafforgue, however, does not compute these spaces at all (except checking some commutative diagrams).
by comparing the Grothendieck-Lefschetz trace formula and Arthur-Selberg trace formula. V. Lafforgue, however, does not compute these spaces at all (except checking some commutative diagrams).
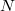 (i.e., which spans a finite dimensional space under the unramified Hecke operators) is exactly the space of cups forms of level
(i.e., which spans a finite dimensional space under the unramified Hecke operators) is exactly the space of cups forms of level 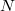 . On the one hand, cusp forms are compactly supported by a theorem of Harder (see Borel-Jacquet 5.2). The space of cups forms of level
. On the one hand, cusp forms are compactly supported by a theorem of Harder (see Borel-Jacquet 5.2). The space of cups forms of level 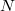 is finite dimensional, hence Hecke finite. On the other hand, let
is finite dimensional, hence Hecke finite. On the other hand, let 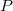 be a rational maximal parabolic subgroup of
be a rational maximal parabolic subgroup of  with Levi subgroup
with Levi subgroup 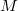 , we would like to show that
, we would like to show that 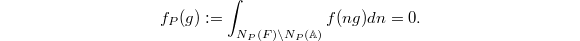 We may assume
We may assume 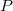 is standard, so
is standard, so 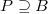 and
and 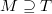 . We may assume that
. We may assume that 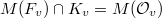 after conjugation. Since
after conjugation. Since 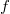 is compactly supported, one can check that
is compactly supported, one can check that 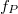 is also compactly supported. On the other hand, the Satake transform
is also compactly supported. On the other hand, the Satake transform 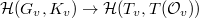 is given by integration on the unipotent radical of
is given by integration on the unipotent radical of 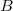 , hence factors through
, hence factors through 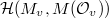 . Because
. Because 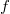 is Hecke finite over
is Hecke finite over 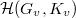 and
and 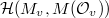 is a finite
is a finite 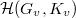 -algebra, it follows that
-algebra, it follows that 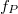 is Hecke finite over
is Hecke finite over 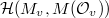 . The center
. The center 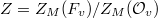 is infinite and preserves the space
is infinite and preserves the space 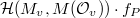 . Since
. Since 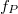 is compactly supported, this contradicts the Hecke finiteness unless
is compactly supported, this contradicts the Hecke finiteness unless 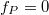 .
.
When 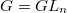 , any Galois representation
, any Galois representation 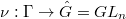 is uniquely determined by its trace function
is uniquely determined by its trace function 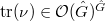 . For general
. For general  , a global parameter
, a global parameter 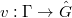 is not determined by any single invariant function. Instead, consider for any
is not determined by any single invariant function. Instead, consider for any 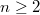 ,
, 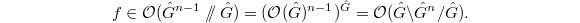 When
When 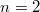 ,
, 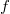 can be identified as a function on the maximal torus invariant under the Weyl group. In general,
can be identified as a function on the maximal torus invariant under the Weyl group. In general, 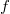 can be thought of as a generalized matrix coefficient, namely there exists a triple
can be thought of as a generalized matrix coefficient, namely there exists a triple 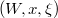 where
where
 ,
,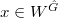 an invariant vector of
an invariant vector of 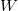 ,
,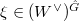 an invariant covector of
an invariant covector of  , such that
, such that 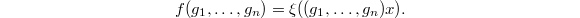
It turns out any  can be uniquely determined as a function on the space of triples
can be uniquely determined as a function on the space of triples  given by
given by 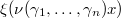 where
where 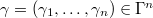 . Our final goal is then to construct such functions on
. Our final goal is then to construct such functions on 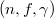 using the geometry of the moduli space of shtukas.
using the geometry of the moduli space of shtukas.
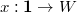 and an annihilation operator
and an annihilation operator 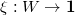 . The diagonal map
. The diagonal map 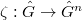 then induces
then induces 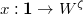 and
and 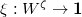 . We define the excursion operator
. We define the excursion operator 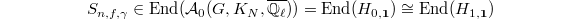 to be the composition:
to be the composition: ![$$H_{1,\mathbf{1}}\xrightarrow{[x]}H_{1,W^\zeta}\cong H_{n,W}\xrightarrow{(\gamma_1,\ldots,\gamma_n)} H_{n,W}\cong H_{1,W^\zeta}\xrightarrow{[\xi]}H_{1,\mathbf{1}}.$$](./latex/VincentLafforgue/latex2png-VincentLafforgue_203016989_.gif) It does not depend on the choice of the triple
It does not depend on the choice of the triple 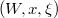 representing
representing  . Let
. Let  be the excursion algebra generated by the excursion operators.
be the excursion algebra generated by the excursion operators.
- The excursion algebra
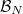 is commutative. For fixed
is commutative. For fixed 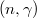 ,
, 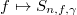 is an algebra morphism.
is an algebra morphism. - (Face relations)
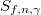 satisfies natural relations subject to morphisms
satisfies natural relations subject to morphisms 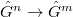 and
and 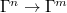 .
. - (Degeneracy relations)
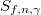 satisfies natural relations subject to multiplications on
satisfies natural relations subject to multiplications on 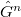 and
and 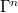 .
. - For fixed
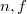 , the homomorphism
, the homomorphism 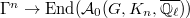 is continuous under the the
is continuous under the the  -adic topology.
-adic topology. - The unramified Hecke algebra
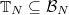 . In fact, for
. In fact, for 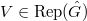 , let
, let 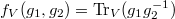 , then
, then 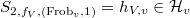 , for
, for 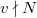 .
.
Let 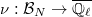 be a character. It turns out (see next section) from this theorem that
be a character. It turns out (see next section) from this theorem that 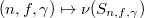 is a
is a 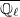 -valued
-valued 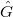 -pseudo-representation of
-pseudo-representation of 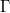 . Our next goal is to make the following theorem precise, hence reduce V. Lafforgue's construction of global Langlands parameters to Theorem 4.
. Our next goal is to make the following theorem precise, hence reduce V. Lafforgue's construction of global Langlands parameters to Theorem 4.
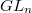 , this is a theorem of R. Taylor. For general groups, it can be deduced from a theorem of Richardson, based on geometric invariant theory.
, this is a theorem of R. Taylor. For general groups, it can be deduced from a theorem of Richardson, based on geometric invariant theory.
02/02/2016
 Pseudo-representations
Pseudo-representations
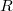 be a topological ring. Let
be a topological ring. Let  be a topological group with unit
be a topological group with unit  . An
. An 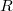 -valued pseudo-representation of
-valued pseudo-representation of  of dimension
of dimension 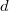 is a continuous function
is a continuous function 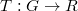 such that
such that
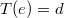 (sometimes also requiring that
(sometimes also requiring that 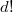 is not a zero divisor in
is not a zero divisor in 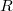 , not needed for V. Lafforgue's work).
, not needed for V. Lafforgue's work).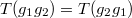 for any
for any 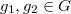 .
.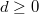 is the smallest integer with the following property: let
is the smallest integer with the following property: let 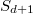 be the symmetric group on
be the symmetric group on 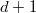 letters and
letters and 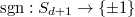 be the sign character, then for all
be the sign character, then for all 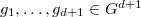 , the following holds:
, the following holds: 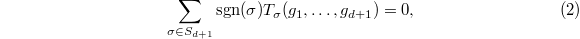 Here if
Here if 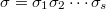 is the is the cycle decomposition,
is the is the cycle decomposition, 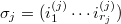 has length
has length 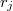 and
and 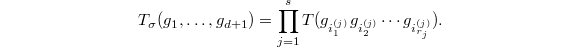
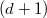 -st exterior power of a
-st exterior power of a 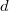 -dimensional vector space is zero.
-dimensional vector space is zero.
- Suppose
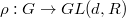 is a continuous representation, then its character
is a continuous representation, then its character 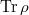 is a pseudo-representation of dimension
is a pseudo-representation of dimension 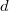 .
. - Conversely, if
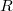 is an algebraically closed field of characteristic zero or
is an algebraically closed field of characteristic zero or 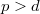 , then any
, then any 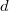 -dimensional pseudo-representation of
-dimensional pseudo-representation of  is the trace of a semisimple representation of dimension
is the trace of a semisimple representation of dimension 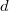 , unique up to homeomorphism.
, unique up to homeomorphism.
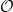 is a
is a 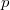 -adic ring with maximal ideal
-adic ring with maximal ideal 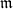 and fraction field
and fraction field 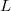 . Suppose for any
. Suppose for any  , we have a torsion representation
, we have a torsion representation 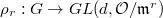 with the compatibility
with the compatibility 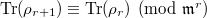 . Then
. Then 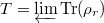 is a pseudo-representation. Hence Theorem 6 implies that
is a pseudo-representation. Hence Theorem 6 implies that 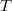 actually comes from a genuine representation
actually comes from a genuine representation 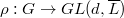 deforming all
deforming all 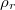 's.
's.
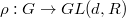 satisfies the identity (2) in (c). Write
satisfies the identity (2) in (c). Write 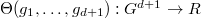 to be the left hand side of (2). Writing
to be the left hand side of (2). Writing  as a quotient of two integral domains of characteristic zero, we reduce to the case that
as a quotient of two integral domains of characteristic zero, we reduce to the case that  is an algebraically closed field of characteristic 0. Let
is an algebraically closed field of characteristic 0. Let 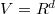 and
and 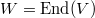 . We may reduce to the universal case
. We may reduce to the universal case 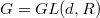 and
and 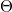 can be viewed as a function on
can be viewed as a function on 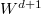 .
.
We observe that 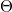 is invariant under
is invariant under 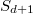 since the the cycle decomposition is invariant under conjugation and
since the the cycle decomposition is invariant under conjugation and 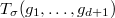 is replaced by
is replaced by 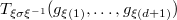 under the action of
under the action of 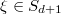 . We can extend
. We can extend 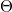 to a multi-linear map on
to a multi-linear map on 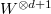 , then
, then 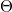 is determined by its values on the subspace of symmetric tensors
is determined by its values on the subspace of symmetric tensors 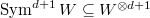 by the invariance under
by the invariance under 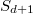 .
.
Since 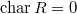 ,
, 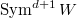 is spanned by symmetric tensors of the form
is spanned by symmetric tensors of the form 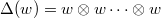 . It remains to show that
. It remains to show that 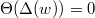 for all
for all 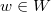 . It suffices to check semisimple
. It suffices to check semisimple  since these semisimple elements are Zariski dense in
since these semisimple elements are Zariski dense in  . Define
. Define 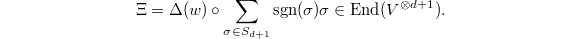 We claim that
We claim that 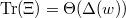 . Since the skew-symmetrization
. Since the skew-symmetrization 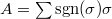 maps
maps 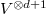 into
into 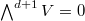 , we know
, we know  . The claim then implies that
. The claim then implies that 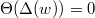 as desired.
as desired.
It remains to prove the claim. Choose a basis 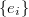 of
of  so that
so that  is diagonalized to be
is diagonalized to be 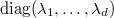 under this basis. Then
under this basis. Then 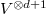 has a basis
has a basis 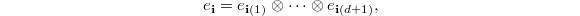 where
where 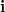 runs all maps
runs all maps ![$[d+1]\rightarrow [d]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_50631650_-5.gif) and
and 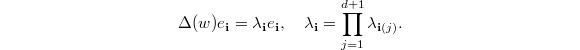 Therefore
Therefore 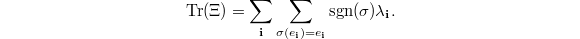 Notice that
Notice that 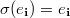 if and only if
if and only if  is constant on each cycle in the cycle decomposition of
is constant on each cycle in the cycle decomposition of 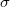 . It follows that
. It follows that 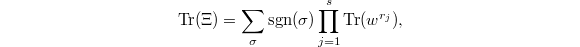 which is equal to
which is equal to 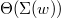 by definition.
¡õ
by definition.
¡õ
For a character 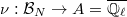 , Theorem 4 gives a continuous algebra homomorphism
, Theorem 4 gives a continuous algebra homomorphism ![$$\Theta_n^{\nu}: \mathcal{O}[\hat G^n\sslash \hat G]\rightarrow C(\Gamma^n, A),\quad f\mapsto \nu(n,f,\gamma).$$](./latex/VincentLafforgue/latex2png-VincentLafforgue_206198037_.gif) By the face relation, for a map
By the face relation, for a map ![$\zeta: [m]\rightarrow [n]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_44436043_-5.gif) , we have
, we have 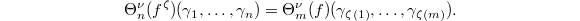 By the degeneracy relation we have
By the degeneracy relation we have 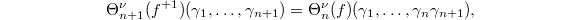 where
where ![$f^{+1}\in \mathcal{O}[\hat G^{n+1}\sslash \hat G]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_45127906_-5.gif) is given by
is given by 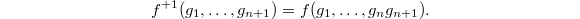 It turns out the collection
It turns out the collection 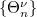 gives a global Langlands parameter
gives a global Langlands parameter 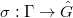 .
.
02/04/2016
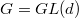 , the global Langlands parameter can be constructed using Theorem 6. Notice that
, the global Langlands parameter can be constructed using Theorem 6. Notice that 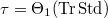 determines all
determines all 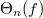 since all representations of
since all representations of 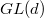 can be constructed from the standard representation using tensor powers. It remains to check that
can be constructed from the standard representation using tensor powers. It remains to check that  satisfies the identity (2). In fact, for
satisfies the identity (2). In fact, for 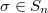 , one can compute that
, one can compute that 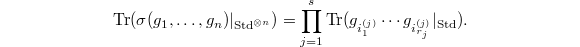 Taking
Taking 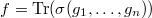 , the degeneracy relation (and
, the degeneracy relation (and 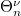 is an algebra homomorphism) implies that
is an algebra homomorphism) implies that 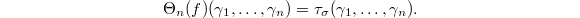 Now take
Now take 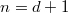 and take skew-symmetrization, we obtain the identity (2) for
and take skew-symmetrization, we obtain the identity (2) for  by using the fact
by using the fact 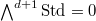 .
.
Now let us consider general  . The construction of the global Langlands parameter does not follow directly from Theorem 6. We need more inputs from geometric invariant theory.
. The construction of the global Langlands parameter does not follow directly from Theorem 6. We need more inputs from geometric invariant theory.
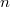 -tuple
-tuple 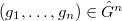 is semisimple if
is semisimple if 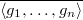 , the Zariski closure of the subgroup generated by
, the Zariski closure of the subgroup generated by 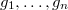 in
in 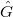 , is semisimple.
, is semisimple.
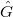 -orbit of
-orbit of 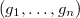 (under conjugation) is Zariski closed in
(under conjugation) is Zariski closed in 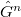 if and only if
if and only if 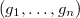 is semisimple.
is semisimple.
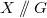 is in bijection with closed orbits of the reductive
is in bijection with closed orbits of the reductive  on the affine variety
on the affine variety  . Thus
. Thus 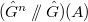 is in bijection with
is in bijection with 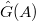 -conjugacy classes of semisimple
-conjugacy classes of semisimple 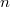 -tuples in
-tuples in 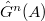 .
.
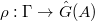 is semisimple if whenever the image of
is semisimple if whenever the image of 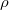 is contained in a parabolic
is contained in a parabolic 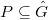 , the
, the 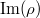 also contained in the Levi of
also contained in the Levi of 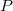 . In characteristic 0, this is the same as saying that the Zariski closure of
. In characteristic 0, this is the same as saying that the Zariski closure of 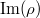 is reductive.
is reductive.
The following theorem constructs a global Langlands parameter 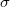 from the collection
from the collection 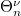 , which makes Theorem 5 more precise.
, which makes Theorem 5 more precise.
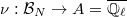 be a homomorphism. Then there is a homomorphism
be a homomorphism. Then there is a homomorphism 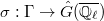 , unique up to conjugacy, such that
, unique up to conjugacy, such that
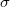 is continuous and takes values in
is continuous and takes values in 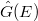 , for a finite extension
, for a finite extension 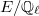 .
.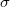 is semisimple.
is semisimple.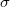 corresponds to
corresponds to  at unramified places under the Satake isomorphism.
at unramified places under the Satake isomorphism.
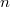 -tuple
-tuple 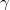 ,
, 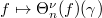 gives a homomorphism
gives a homomorphism ![$\mathcal{O}[\hat G^n\sslash \hat G]\rightarrow A$](./latex/VincentLafforgue/latex2png-VincentLafforgue_47154924_-5.gif) , i.e. a point in
, i.e. a point in 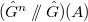 . Let
. Let 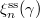 be the corresponding semisimple conjugacy class in
be the corresponding semisimple conjugacy class in 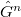 given by Theorem 7.
given by Theorem 7.
Choose 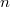 ,
, 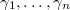 and a representative
and a representative 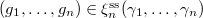 so that
so that
- (H1)
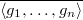 is of maximal dimension.
is of maximal dimension. - (H2) The centralizer
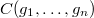 of
of 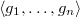 (which is also the centralizer of the Zariski closure) is of the smallest dimension with smallest number of connected components.
(which is also the centralizer of the Zariski closure) is of the smallest dimension with smallest number of connected components.
Let 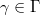 , we define
, we define 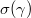 to be
to be 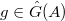 such that
such that 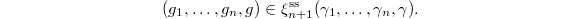 We need to verify the following:
We need to verify the following:
- (A) Such
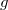 exists.
exists. - (B) Such
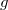 is unique.
is unique. - (C) The map
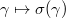 is a homomorphism.
is a homomorphism. - (D) The map
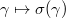 is continuous.
is continuous.
Let 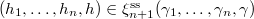 . We will show that the
. We will show that the 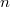 -tuple
-tuple 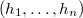 is semisimple. In fact, the face relation implies that
is semisimple. In fact, the face relation implies that 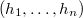 lies over
lies over 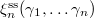 . Theorem 5.2 of Richardson then implies that
. Theorem 5.2 of Richardson then implies that 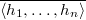 has a Levi isomorphic to
has a Levi isomorphic to 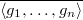 . By (H1), they must have the same dimension. Hence
. By (H1), they must have the same dimension. Hence 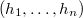 is semisimple and thus equal to
is semisimple and thus equal to 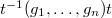 for some
for some 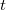 . Therefore
. Therefore 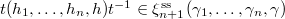 . We can then define
. We can then define 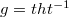 , which proves (A).
, which proves (A).
Since 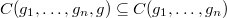 , by (H2) we know that they must be equal. The uniqueness of
, by (H2) we know that they must be equal. The uniqueness of 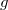 (B) then follows from the fact that
(B) then follows from the fact that 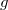 lies in the center of
lies in the center of 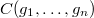 . The degeneracy relation implies that
. The degeneracy relation implies that 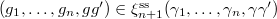 . Hence (C) follows from the uniqueness.
. Hence (C) follows from the uniqueness.
Notice 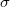 takes value in a reductive group
takes value in a reductive group 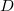 , the center of
, the center of 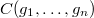 . To show (D), it suffices to show that for any
. To show (D), it suffices to show that for any ![$\phi\in \mathcal{O}[D]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_152830549_-5.gif) , the composition
, the composition 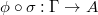 is continuous. It follows from geometric invariant theory that the map
is continuous. It follows from geometric invariant theory that the map ![$$q: \mathcal{O}[\hat G^{n+1}\sslash \hat G]\rightarrow \mathcal{O}[D], \quad f\mapsto (g\mapsto f(g_1,\ldots,g_n,g))$$](./latex/VincentLafforgue/latex2png-VincentLafforgue_12553338_.gif) is surjective. If we lift
is surjective. If we lift  to
to  , then by the construction of
, then by the construction of 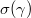 we know that
we know that 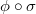 is equal to the map
is equal to the map 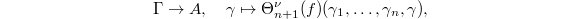 which is continuous.
¡õ
which is continuous.
¡õ
The rest of the course will focus on proving Theorem 4, using the geometry of moduli spaces of shtukas.
02/09/2016
 Moduli of
Moduli of  -bundles
-bundles
Our next goal is to explain that 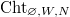 , the moduli space of shtukas of level
, the moduli space of shtukas of level 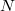 with no paws, is the discrete stack
with no paws, is the discrete stack 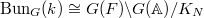 . Since the IC sheaf on the discrete stack is simply the constant sheaf
. Since the IC sheaf on the discrete stack is simply the constant sheaf 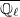 , it follows that
, it follows that 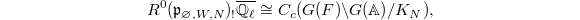 whose Hecke finite is exactly the space of cusp forms (Remark 11).
whose Hecke finite is exactly the space of cusp forms (Remark 11).
 be a scheme over
be a scheme over 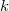 . Let
. Let  be an affine group scheme over
be an affine group scheme over 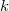 . The following data (called a
. The following data (called a  -bundle) are equivalent:
-bundle) are equivalent:
- A sheaf
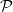 on the fpqc site of
on the fpqc site of  with a left action of
with a left action of  such that
such that 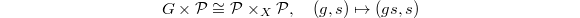 is an isomorphism and there exists an fpqc cover
is an isomorphism and there exists an fpqc cover 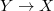 with
with 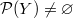 (local triviality in fpqc topology).
(local triviality in fpqc topology). - A scheme
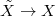 with a left action of
with a left action of  and an fpqc cover
and an fpqc cover 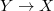 such that
such that 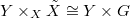 in a
in a  -equivariant way.
-equivariant way. - An fpqc scheme
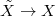 with a left action of
with a left action of  such that
such that 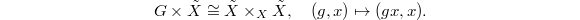
 as in (a). Then
as in (a). Then 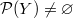 implies that
implies that 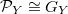 is trivial. The existence of the scheme
is trivial. The existence of the scheme 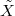 then follows from fpqc descent for affine morphisms since
then follows from fpqc descent for affine morphisms since 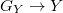 is affine.
is affine.
(b) to (a): take 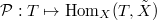 .
.
(b) to (c): it follows from fpqc descent for isomorphisms.
(c) to (b): take  .
¡õ
.
¡õ
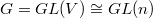 . Let
. Let 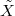 be a
be a  -bundle over
-bundle over  . Then the associated bunlde
. Then the associated bunlde 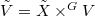 is a rank
is a rank 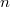 vector bundle. This gives a functor from
vector bundle. This gives a functor from  -bundle on
-bundle on  to rank
to rank 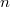 vector bundle on
vector bundle on  . It is an equivalence of groupoids. The inverse functor sends a vector bundle
. It is an equivalence of groupoids. The inverse functor sends a vector bundle 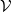 on
on  to the fpqc sheaf
to the fpqc sheaf 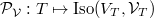 .
.
More generally, let 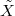 be a
be a  -bundle over
-bundle over  . If
. If 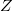 is affine (or quasi-projective with a
is affine (or quasi-projective with a  -equivariant ample line bundle), then then quotient
-equivariant ample line bundle), then then quotient 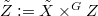 always exists. This defines a functor
always exists. This defines a functor 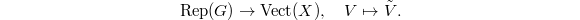 It is exact, commutes with direct sum, tensor product and sends the trivial representation to the trivial bundle.
It is exact, commutes with direct sum, tensor product and sends the trivial representation to the trivial bundle.
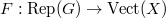 , we would like to define a
, we would like to define a  -bundle
-bundle 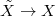 . We can extend
. We can extend 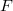 to direct limits of finite dimensional represetations by
to direct limits of finite dimensional represetations by 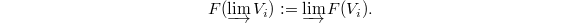 Since each
Since each 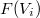 is a vector bundle on
is a vector bundle on  and flatness is preserved under direct limit, we know that
and flatness is preserved under direct limit, we know that 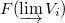 is a flat
is a flat 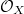 -module. Take
-module. Take ![$V=k[G]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_265264563_-5.gif) to be the regular representation, then
to be the regular representation, then 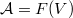 is a
is a 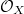 -algebra, flat as an
-algebra, flat as an 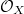 -module. Define the scheme
-module. Define the scheme 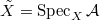 . Then
. Then 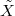 is flat over
is flat over  and admits a
and admits a  -action over
-action over  . By the exactness of
. By the exactness of 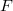 , the short exact sequence
, the short exact sequence ![$$0\rightarrow k\rightarrow k[G]\rightarrow k[G]/k\rightarrow0$$](./latex/VincentLafforgue/latex2png-VincentLafforgue_38171853_.gif) induces an exact sequence
induces an exact sequence ![$$0\rightarrow \mathcal{O}_X\rightarrow \mathcal{A}\rightarrow F(k[G]/k)\rightarrow0.$$](./latex/VincentLafforgue/latex2png-VincentLafforgue_204627231_.gif) Because
Because ![$F(k[G]/k)$](./latex/VincentLafforgue/latex2png-VincentLafforgue_98843919_-5.gif) is a flat
is a flat 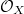 -module, we know that
-module, we know that 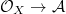 remains injective when reducing any maximal ideal. In particular,
remains injective when reducing any maximal ideal. In particular, 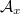 is not zero for all
is not zero for all 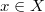 . Hence
. Hence 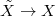 is surjective. Since for any representation
is surjective. Since for any representation 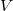 , the
, the  -representation
-representation ![$k[G] \otimes V$](./latex/VincentLafforgue/latex2png-VincentLafforgue_213474554_-5.gif) is isomorphic to
is isomorphic to ![$k[G]\otimes \mathbf{V}$](./latex/VincentLafforgue/latex2png-VincentLafforgue_30179953_-5.gif) , where
, where 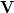 is the vector space underlying
is the vector space underlying 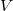 with trivial
with trivial  -action. It follows from
-action. It follows from 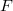 is a tensor functor that
is a tensor functor that ![$$\tilde X\times_X\tilde X = \Spec_X(F(k[G] \otimes k[G])) \cong \Spec_X(F(k[G]) \otimes \mathcal{O}_X[G])) = \tilde X\times G.$$](./latex/VincentLafforgue/latex2png-VincentLafforgue_39022759_.gif) is a
is a  -equivariant isomorphism.
¡õ
-equivariant isomorphism.
¡õ
02/16/2016
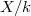 be a projective scheme. Then the functor
be a projective scheme. Then the functor 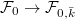 induces an equivalence between the category of coherent sheaves on
induces an equivalence between the category of coherent sheaves on  and the category of pairs
and the category of pairs 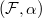 , where
, where 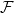 is a coherent sheaf on
is a coherent sheaf on 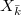 and
and 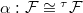 . Here if
. Here if 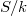 is a scheme, then
is a scheme, then 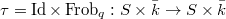 .
.
 be a very ample line bundle on
be a very ample line bundle on  . The functor
. The functor 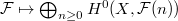 gives an equivalence between coherent sheaves on
gives an equivalence between coherent sheaves on  and the quotient category of graded modules of finite type over
and the quotient category of graded modules of finite type over 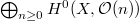 modulo the subcategory of eventually zero modules. We have a similar functor for
modulo the subcategory of eventually zero modules. We have a similar functor for 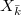 , which also commutes with
, which also commutes with  . Using this equivalence we are reduced to the case when
. Using this equivalence we are reduced to the case when  is a point, which follows from the following lemma (Galois descent over finite fields).
¡õ
is a point, which follows from the following lemma (Galois descent over finite fields).
¡õ
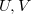 be vector spaces over
be vector spaces over  . Let
. Let 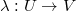 be a
be a 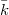 -linear map and let
-linear map and let 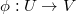 be a
be a 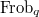 -semi-linear map. Let
-semi-linear map. Let 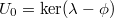 . Then
. Then
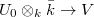 is injective if
is injective if 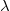 is injective;
is injective;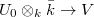 is bijective if
is bijective if 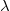 and
and 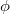 are bijective.
are bijective.
- Suppose
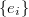 is a
is a 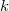 -basis of
-basis of 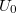 , we need to show that
, we need to show that 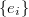 are linearly independent over
are linearly independent over 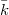 . Suppose there is a relation
. Suppose there is a relation 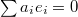 . Apply
. Apply 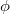 and use the definition of
and use the definition of 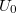 and the injectivity of
and the injectivity of 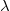 , we obtain that
, we obtain that 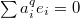 . It follows that
. It follows that 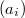 is a scalar multiple of
is a scalar multiple of 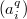 . Hence all
. Hence all 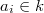 , by Hilbert 90, thus the relation
, by Hilbert 90, thus the relation 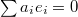 must be trivial.
must be trivial. - It suffices to show that
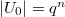 , if
, if 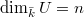 . Let
. Let 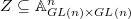 be a closed subscheme defined by
be a closed subscheme defined by 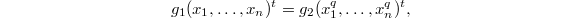 where
where 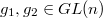 are the matrices corresponding to
are the matrices corresponding to 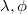 . Using the addition on
. Using the addition on 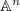 , this becomes an affine group scheme over
, this becomes an affine group scheme over 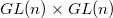 . One can check that it is also etale by computing the relative differential. Let
. One can check that it is also etale by computing the relative differential. Let 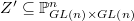 be its Zariski closure. In homogeneous coordinates we have
be its Zariski closure. In homogeneous coordinates we have 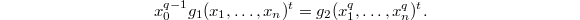 So
So 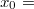 implies that all
implies that all 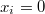 , i.e.,
, i.e., 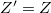 . It follows that
. It follows that 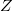 is in fact finite over
is in fact finite over 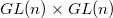 . But the fiber over
. But the fiber over 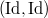 is nothing but
is nothing but 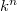 , hence the fibers have constant cardinality
, hence the fibers have constant cardinality 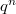 .
¡õ
.
¡õ
Now let us come back to the situation that  is a smooth projective curve over
is a smooth projective curve over 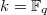 . Let
. Let 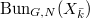 (resp.
(resp. 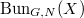 ) be the moduli stack of
) be the moduli stack of  bundles on
bundles on 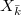 (resp.
(resp.  ) with a trivialization along
) with a trivialization along 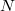 . We obtain the following corollary.
. We obtain the following corollary.
Let us consider the case 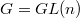 . In this case
. In this case 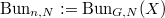 is the moduli stack of vector bundle of rank
is the moduli stack of vector bundle of rank 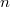 with trivialization along
with trivialization along 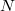 . Consider the tuples
. Consider the tuples 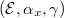 , where
, where
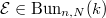 ,
,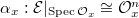 , where
, where 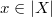 ,
,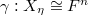 , where
, where 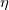 is the generic point of
is the generic point of  .
.
From this tuple we can define 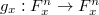 given by
given by 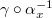 . Then
. Then 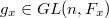 . Since
. Since 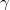 is integral at
is integral at  for almost all
for almost all 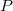 , we know that
, we know that 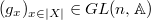 . Forgetting
. Forgetting 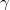 and replacing
and replacing 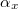 by the given trivialization
by the given trivialization 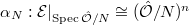 amounts to taking quotient by
amounts to taking quotient by 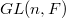 on one side and by
on one side and by 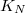 on the other side. Conversely, an element
on the other side. Conversely, an element 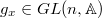 gives a projective module of rank
gives a projective module of rank 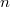 over each affine open of
over each affine open of  (since projective modules over a Dedekind domain are equivalent to its local data) and they glue together to a rank
(since projective modules over a Dedekind domain are equivalent to its local data) and they glue together to a rank 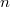 vector bundle on
vector bundle on  . So we obtain Weil's uniformization
. So we obtain Weil's uniformization 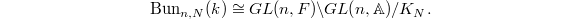
For general  , we need the following theorem (Hasse principle):
, we need the following theorem (Hasse principle):
 be a split reductive connected group. Then
be a split reductive connected group. Then 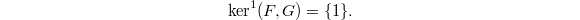 Here
Here 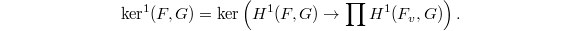
Notice any  -bundle over
-bundle over  becomes locally trivial by Lang's theorem and Hensel's lemma. This theorem implies that the generic fiber of any
becomes locally trivial by Lang's theorem and Hensel's lemma. This theorem implies that the generic fiber of any  -bundle over
-bundle over  is trivial as well. Hence we obtain the same uniformization for general
is trivial as well. Hence we obtain the same uniformization for general  using Tannakian formalism (Theorem 9),
using Tannakian formalism (Theorem 9), 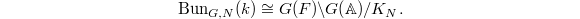
02/18/2016
Notice  is not of finite type as one can easily see from the example of
is not of finite type as one can easily see from the example of 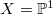 . The Harder-Narasimhan (i.e. slope) filtration of vector bundle on curves naturally gives a stratification on
. The Harder-Narasimhan (i.e. slope) filtration of vector bundle on curves naturally gives a stratification on 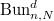 such that the strata with bounded slopes become finite type. For general
such that the strata with bounded slopes become finite type. For general  , we choose
, we choose 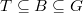 a maximal torus and a Borel. Let
a maximal torus and a Borel. Let 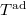 be the image of
be the image of 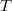 in
in 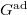 . Let
. Let 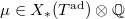 , which one can think of as the "slopes" for a
, which one can think of as the "slopes" for a  -bundle.
-bundle.
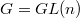 , if a vector bundle
, if a vector bundle 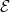 has slope corresponding to
has slope corresponding to 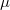 . Then one can see that the
. Then one can see that the 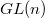 -structure of
-structure of 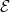 can be reduced to the parabolic subgroup
can be reduced to the parabolic subgroup 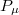 associated to
associated to 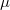 . Intuitively smaller parabolics correspond to more degenerate "cusps" of
. Intuitively smaller parabolics correspond to more degenerate "cusps" of 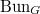 . In fact, one can use this correspondence to give a geometric proof of Remark 11.
. In fact, one can use this correspondence to give a geometric proof of Remark 11.
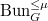 to be the substack of
to be the substack of 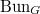 such that for any dominant weight
such that for any dominant weight 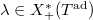 , any geometric point
, any geometric point 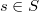 and any
and any 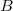 structure
structure 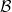 on
on 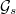 , we have
, we have 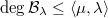 . Here a
. Here a  -structure on
-structure on 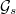 means a
means a 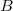 -bundle
-bundle 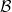 such that
such that 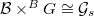 and
and 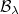 is the line bundle associated to
is the line bundle associated to 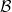 using the 1-dimensional representation
using the 1-dimensional representation 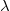 of
of 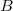 .
.
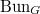 parallels Arthur's truncation process in the trace formula. In fact a comparison between them already appeared in the work of L. Lafforgue.
parallels Arthur's truncation process in the trace formula. In fact a comparison between them already appeared in the work of L. Lafforgue.
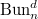 is represented by an algebraic stack, locally of finite type.
is represented by an algebraic stack, locally of finite type.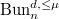 is an open substack.
is an open substack.- If
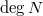 is sufficiently large (relative to
is sufficiently large (relative to 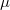 ), then
), then 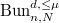 is a smooth quasi-projective scheme.
is a smooth quasi-projective scheme.
 . In fact, the
. In fact, the 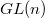 case implies the general case: one can embed
case implies the general case: one can embed  into some
into some 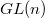 to view
to view  -bundles as vector bundles with
-bundles as vector bundles with  -structure and deduce the relative representativity of
-structure and deduce the relative representativity of 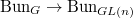 from that the quotient
from that the quotient 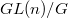 is affine (since
is affine (since  is reductive). See Behrend's thesis, Sec 4.
is reductive). See Behrend's thesis, Sec 4.
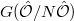 acts on the level structure and hence acts on the stack
acts on the level structure and hence acts on the stack 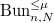 . Hence (c) implies that the quotient stack
. Hence (c) implies that the quotient stack 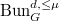 is Deligne-Mumford and of finite type. This together with (b) implies (a).
is Deligne-Mumford and of finite type. This together with (b) implies (a).
Let us briefly sketch the proof of the algebraicity statement (c). Fix an ample line bundle 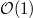 on
on  . For fixed
. For fixed 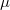 , there exists an integer
, there exists an integer 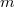 such that for any
such that for any 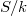 , and any
, and any 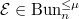 , the following (relative version of Serre's theorem, uniform in
, the following (relative version of Serre's theorem, uniform in 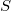 ) holds:
) holds:
- The direct image
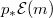 is a vector bundle, where
is a vector bundle, where 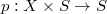 is the projection.
is the projection. 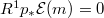 .
.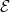 is generated by
is generated by 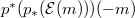 .
.
Moreover, for fixed 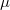 and
and 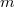 , when
, when 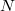 with sufficiently larger degree, the vector bundle
with sufficiently larger degree, the vector bundle 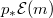 is a subbundle of
is a subbundle of 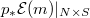 . Using the level
. Using the level 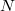 structure, we can then embed
structure, we can then embed 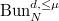 into the moduli space classifying pairs
into the moduli space classifying pairs 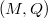 , where
, where 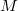 is a subbundle of
is a subbundle of 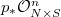 of fixed rank and
of fixed rank and 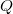 is a locally free quotient of
is a locally free quotient of 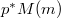 of rank
of rank 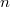 and degree
and degree 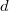 . The latter moduli space is a generalized Grassmannian represented by a quasi-projective scheme (using Grothendieck's Quot scheme construction). The smoothness follows from the vanishing of
. The latter moduli space is a generalized Grassmannian represented by a quasi-projective scheme (using Grothendieck's Quot scheme construction). The smoothness follows from the vanishing of 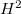 for curves.
for curves.
03/01/2016
 Affine Grassmannians and Beilinson-Drinfeld affine Grassmannians
Affine Grassmannians and Beilinson-Drinfeld affine Grassmannians
Let ![$\mathcal{O}=k[ [t] ]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_215040117_-5.gif) and
and 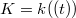 . Let
. Let  be a split group. Let
be a split group. Let 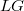 (resp.
(resp. 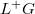 ) be the loop (resp. positive loop) group. Let
) be the loop (resp. positive loop) group. Let 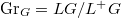 be the affine Grassmannian. All these are ind-schemes over
be the affine Grassmannian. All these are ind-schemes over 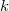 . We have
. We have 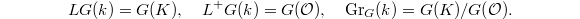 I was notified by X. Zhu during the weekend that there are some gaps in the literature on the foundation of affine Grassmannians. His recent PCMI notes Introduction to Affine Grassmannians filled the gaps.
I was notified by X. Zhu during the weekend that there are some gaps in the literature on the foundation of affine Grassmannians. His recent PCMI notes Introduction to Affine Grassmannians filled the gaps.
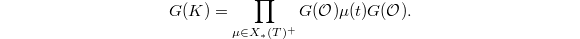 It defines an invariant map
It defines an invariant map 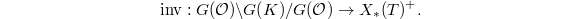 For
For  , we define
, we define 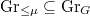 to classify pairs
to classify pairs 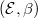 , where
, where 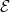 is a
is a  -bundle on the disk
-bundle on the disk 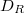 and
and 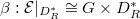 is a trivialization on the puncture disk
is a trivialization on the puncture disk 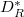 such that the invariant
such that the invariant 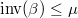 . We endow it with the closed reduced subscheme structure. We further define
. We endow it with the closed reduced subscheme structure. We further define 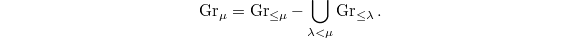
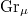 is a single
is a single 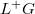 -orbit. It is a smooth quasi-projective variety of dimension
-orbit. It is a smooth quasi-projective variety of dimension 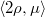 . Moreover,
. Moreover, 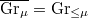 is a (possibly singular) projective variety.
is a (possibly singular) projective variety.
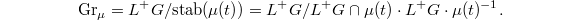 It follows that
It follows that 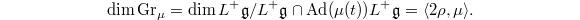 The smoothness follows since it is an orbit of the group. The claim
The smoothness follows since it is an orbit of the group. The claim 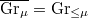 can be seen by doing long combinatorics or reducing to the case of
can be seen by doing long combinatorics or reducing to the case of 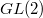 inductively.
¡õ
inductively.
¡õ
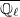 -IC sheaves on
-IC sheaves on 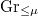 form a basis (when varying
form a basis (when varying 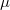 ) of the abelian category of
) of the abelian category of 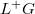 -equivariant perverse sheaves
-equivariant perverse sheaves 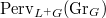 on
on 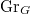 . Our next goal is to give a multiplicative structure (convolution product) on perverse sheaves and prove this product is commutative. This is the analogue of the commutativity of the spherical Hecke algebra. Under the sheaf-function dictionary this indeed recovers the convolution on the classical Hecke algebra. Moreover, taking (appropriate signed summation of) the cohomology provides a fiber functor. This gives
. Our next goal is to give a multiplicative structure (convolution product) on perverse sheaves and prove this product is commutative. This is the analogue of the commutativity of the spherical Hecke algebra. Under the sheaf-function dictionary this indeed recovers the convolution on the classical Hecke algebra. Moreover, taking (appropriate signed summation of) the cohomology provides a fiber functor. This gives 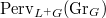 a neutral Tannakian structure and hence we can abstractly identify
a neutral Tannakian structure and hence we can abstractly identify 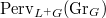 with the category of representations of an affine group
with the category of representations of an affine group 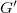 . The content of the geometric Satake correspondence is that
. The content of the geometric Satake correspondence is that 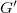 is exactly the Langlands dual group
is exactly the Langlands dual group 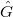 . Under the sheaf-function dictionary, this indeed recovers the classical Satake isomorphism.
. Under the sheaf-function dictionary, this indeed recovers the classical Satake isomorphism.
The proof (we will follow Richarz's proof) of geometric Satake requires global input: the Beilinson-Drinfeld affine Grassmannian (a global analogue of the affine Grassmannian).
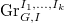 to be the (ind-)stack classifying the same data as the Hecke stack (see Definition 14)
to be the (ind-)stack classifying the same data as the Hecke stack (see Definition 14) 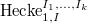 (with no level structure) plus a trivialization for the last
(with no level structure) plus a trivialization for the last  -bundle
-bundle 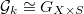 along
along  . Notice we recover the usual affine Grassmannian when there is only one point of modification (
. Notice we recover the usual affine Grassmannian when there is only one point of modification (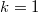 ,
, 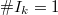 ).
).
The similar proof as in the case of affine Grassmannians gives:
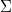 be the moduli space of relative effective Cartier divisors on
be the moduli space of relative effective Cartier divisors on  . Then
. Then 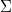 is represented by
is represented by 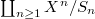 . Let
. Let 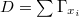 be such a divisor. We write
be such a divisor. We write 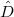 be the formal completion of
be the formal completion of  along
along 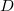 and
and 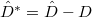 . We define the Beilinson-Drinfeld Grassmannian
. We define the Beilinson-Drinfeld Grassmannian 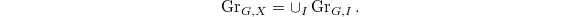 It is an ind-scheme, ind-proper over
It is an ind-scheme, ind-proper over 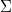 .
.
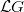 (resp.
(resp. 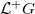 ) to be the global loop group (resp. the global positive loop group), classifying pairs
) to be the global loop group (resp. the global positive loop group), classifying pairs 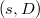 , where
, where 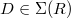 and
and 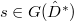 (resp.
(resp. 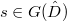 ).
).
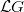 is represented by an ind-group scheme over
is represented by an ind-group scheme over 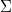 . It classifies tuples
. It classifies tuples 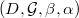 , where
, where 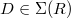 ,
, 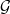 a
a  -torsor on
-torsor on  ,
, 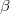 a trivialization of
a trivialization of 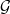 away from
away from 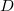 ,
, 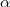 a trivialization along
a trivialization along 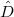 .
.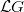 is represented by an ind-group scheme over
is represented by an ind-group scheme over 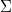 .
.- The map
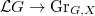 given by forgetting
given by forgetting 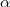 is a right
is a right 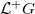 -torsor and induces an isomorphism of fpqc sheaves over
-torsor and induces an isomorphism of fpqc sheaves over 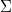 ,
, 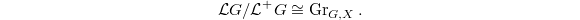
03/29/2016
 Moduli of shtukas
Moduli of shtukas
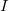 be a finite set and
be a finite set and 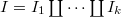 be a partition. We define the Hecke stack
be a partition. We define the Hecke stack 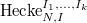 to be the moduli stack whose
to be the moduli stack whose 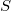 -points are given by tuples consisting of:
-points are given by tuples consisting of:
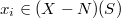 ,
, 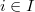 .
.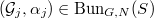 ,
, 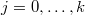 .
.- Isomorphisms
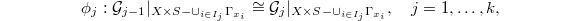 compatible with the level structure
compatible with the level structure 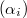 .
.
In other words, a point in the Hecke stack is a length 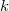 sequence of modifications of
sequence of modifications of  -bundles and the
-bundles and the 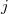 -th modification has prescribed location
-th modification has prescribed location 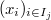 . We can further restrict the order of poles for these modifications.
. We can further restrict the order of poles for these modifications.
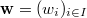 be an
be an 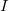 -tuple of dominant coweights of
-tuple of dominant coweights of  . We define
. We define 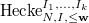 to be the closed substack of
to be the closed substack of 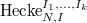 such that for all dominant weights
such that for all dominant weights 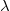 of
of  ,
, 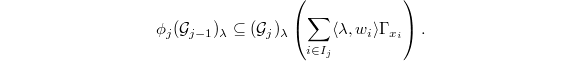 Here
Here 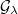 is the vector bundle associated to
is the vector bundle associated to 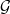 using the finite dimensional representation of
using the finite dimensional representation of  of highest weight
of highest weight 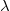 .
.
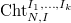 to be the stack over
to be the stack over 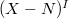 classifying the data (a-c) together with an isomorphism
classifying the data (a-c) together with an isomorphism 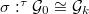 preserving the level structure. Thus we have a Cartesian diagram
preserving the level structure. Thus we have a Cartesian diagram ![$$\xymatrix{\Cht_{N,I}^{I_1,\ldots, I_k} \ar[r] \ar[d] & \Hecke_{N,I}^{I_1,\ldots,I_k} \ar[d] \\ \Bun_{G,N} \ar[r]^-{(\Id,\Frob_q)} & \Bun_{G,N} \times \Bun_{G,N} .}$$](./latex/VincentLafforgue/latex2png-VincentLafforgue_172066369_.gif)
Similarly define 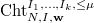 .
.
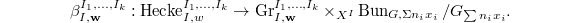 Here
Here 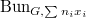 parametrizes a
parametrizes a  bundle
bundle  together with a trivialization along
together with a trivialization along 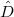 modulo the equivalence mod
modulo the equivalence mod 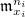 .
.
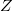 an effective divisor on
an effective divisor on  ,
, 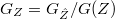 (a finite dimensional quotient of two infinite dimensional objects). The quotient by
(a finite dimensional quotient of two infinite dimensional objects). The quotient by 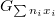 concretely means forgetting the trivialization
concretely means forgetting the trivialization 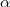 along
along 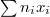 . The morphism
. The morphism 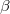 is the same as a
is the same as a 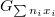 -torsor
-torsor 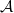 over
over 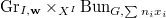 . In terms of moduli interpretation, the above isomorphism is simply reorganizing the same data.
. In terms of moduli interpretation, the above isomorphism is simply reorganizing the same data.
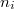 is sufficiently large relative to
is sufficiently large relative to 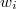 , then the action of
, then the action of 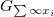 on
on 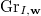 factors through a finite dimensional quotient.
factors through a finite dimensional quotient.
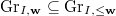 be the reduced closed subscheme given by the Zariski closure of
be the reduced closed subscheme given by the Zariski closure of 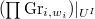 , where
, where 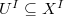 is the complement of all diagonals. Define
is the complement of all diagonals. Define 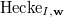 be the inverse image of
be the inverse image of 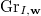 .
.
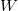 a finite dimensional representation of
a finite dimensional representation of 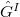 , we define
, we define 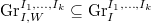 to be the union of
to be the union of 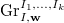 where the representation
where the representation 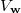 appears in
appears in 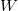 . Define
. Define 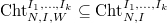 using
using 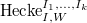 similarly.
similarly.
We have a map analogous to the map 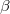 ,
, 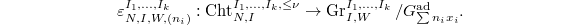
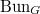 is smooth and the derivative of Frobenius is zero.
¡õ
is smooth and the derivative of Frobenius is zero.
¡õ
Now we can restate the geometric Satake correspondence for all possible parameters (Theorem 1.17 in V. Lafforgue's paper).
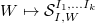 from the representations of
from the representations of 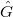 to
to 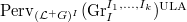 (universally locally acyclic equivariant perverse sheaves). The support of
(universally locally acyclic equivariant perverse sheaves). The support of 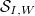 lies in
lies in 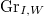 .
.
- If
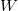 is irreducible, then
is irreducible, then 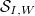 is the IC sheaf of
is the IC sheaf of 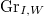 .
. - Suppose
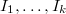 is a refinement of
is a refinement of 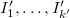 , this induces natural maps
, this induces natural maps 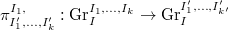 (and similarly for
(and similarly for  ). These maps turns out to be small and hence maps IC sheaves to IC sheaves and
). These maps turns out to be small and hence maps IC sheaves to IC sheaves and 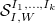 to
to 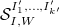 .
. - Suppose
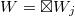 , where
, where 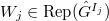 . Then
. Then 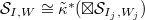 , where
, where 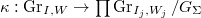 .
. - Suppose
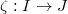 and
and 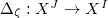 . Let
. Let 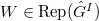 and
and 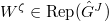 via pullback. Let
via pullback. Let 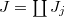 and
and 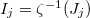 . Then we have isomorphisms, functorial in
. Then we have isomorphisms, functorial in 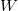 ,
, 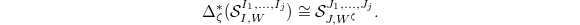 Here
Here 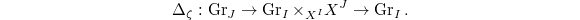
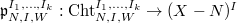 be the paw morphism. We define
be the paw morphism. We define 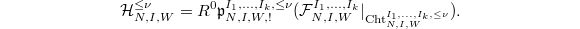 Notice the result does not depend on the partition of
Notice the result does not depend on the partition of 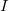 , which is a consequence of the smallness in b).
, which is a consequence of the smallness in b).
03/31/2016
 Excursion operators
Excursion operators
The local system 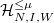 corresponds to a
corresponds to a 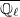 -local system on the arithmetic etale fundamental group
-local system on the arithmetic etale fundamental group 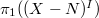 , which is an extension of
, which is an extension of 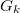 by the geometric etale fundamental group. Drinfeld's lemma (see the next section) allows us to extend the action of
by the geometric etale fundamental group. Drinfeld's lemma (see the next section) allows us to extend the action of 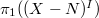 to
to 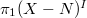 (the latter has
(the latter has 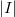 copies of
copies of 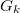 ).
).
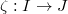 . Let
. Let 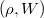 be a finite dimensional representation of
be a finite dimensional representation of 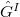 . Then there is a canonical coalescence isomorphism
. Then there is a canonical coalescence isomorphism 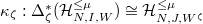 .
.
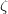 is injective and surjective.
is injective and surjective.
- Suppose
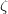 is injective. For simplicity let us assume
is injective. For simplicity let us assume 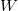 is irreducible. The shtukas in question involves no modification along
is irreducible. The shtukas in question involves no modification along 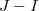 (since
(since 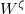 is a trivial representation of
is a trivial representation of 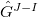 ). So we have a canonical isomorphism
). So we have a canonical isomorphism 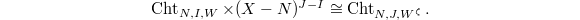 (In particular, the
(In particular, the 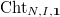 is nothing but
is nothing but 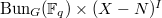 .)
.) - Suppose
 is surjective. Then
is surjective. Then 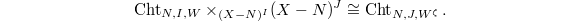 It follows from d) of Theorem 15 that
It follows from d) of Theorem 15 that 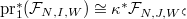 . The result then follows from proper base change.
¡õ
. The result then follows from proper base change.
¡õ
Taking 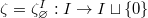 and
and 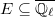 be the trivial representation, we obtain the isomorphism
be the trivial representation, we obtain the isomorphism 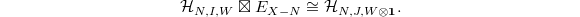 Taking
Taking 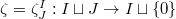 , we obtain the isomorphism
, we obtain the isomorphism 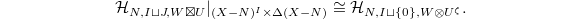 Now combining these two isomorphisms we can define the creation/annihilation operators.
Now combining these two isomorphisms we can define the creation/annihilation operators.
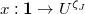 be an invariant vector. Let
be an invariant vector. Let 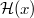 be the corresponding morphism on cohomology. We define the creation operator to be
be the corresponding morphism on cohomology. We define the creation operator to be 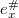 to be the composition
to be the composition 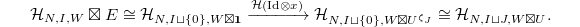 Similarly define the annihilation operator
Similarly define the annihilation operator 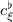 for
for 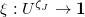 an invariant covector.
an invariant covector.
- The creation and annihilation operators commute when the paws are disjoint.
- The composition of two creation/annihilation operators correspond to disjoint set of paws is the creation/annihilation operators for their union.
04/07/2016
 Partial Frobenius operators
Partial Frobenius operators
Reference: thesis of Eike Lau and L. Lafforgue.
Theorem 10 has the following consequence:
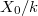 be smooth of finite type. Let
be smooth of finite type. Let 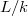 be algebraically closed. Let
be algebraically closed. Let 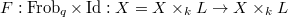 . Then the functor
. Then the functor 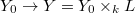 gives an equivalence between finite etale covers
gives an equivalence between finite etale covers 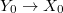 and finite etale covers
and finite etale covers 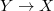 together with an isomorphism
together with an isomorphism 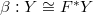 .
.
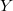 as relative spectrum
as relative spectrum 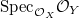 . For any
. For any 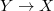 finite etale, we have
finite etale, we have 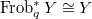 (see Stacks project 50.79). So the isomorphism
(see Stacks project 50.79). So the isomorphism 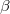 is equivalent to the isomorphism
is equivalent to the isomorphism 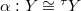 since
since 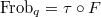 . The same argument as in Theorem 10 gives that
. The same argument as in Theorem 10 gives that 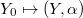 is fully faithful.
is fully faithful.
The hard part is to show the essential surjectivity. By fully faithfulness it suffices to deal with the case  is affine. Let
is affine. Let 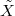 be a compactification, let
be a compactification, let 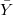 be the normalization of
be the normalization of 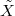 in the function field
in the function field 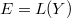 . Because
. Because  is smooth, we know that
is smooth, we know that 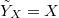 . So we are in a situation of a normal morphism between projective schemes, which on an open part becomes etale. Since
. So we are in a situation of a normal morphism between projective schemes, which on an open part becomes etale. Since  does not change the scheme (but only change the
does not change the scheme (but only change the 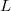 -structure),
-structure), 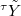 is the normalization of
is the normalization of 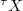 in
in 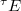 . Since normalization is canonical, it follows that
. Since normalization is canonical, it follows that 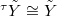 . By Theorem ##VLgaloisdescent applying to the projective scheme
. By Theorem ##VLgaloisdescent applying to the projective scheme 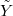 , we get
, we get 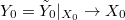 . Since
. Since  is etale, we know that
is etale, we know that  is also etale (by base change).
¡õ
is also etale (by base change).
¡õ
 be the fundamental groupoid of
be the fundamental groupoid of  , whose objects are geometric points of
, whose objects are geometric points of  and morphisms are the isomorphisms
and morphisms are the isomorphisms  . Here
. Here 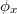 is the fiber functor at
is the fiber functor at 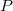 from the category of finite etale coverings of
from the category of finite etale coverings of  to sets.
to sets.
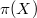 is a functor from
is a functor from 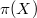 to sets, namely, a collection of sets
to sets, namely, a collection of sets 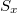 together with
together with 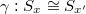 for any
for any 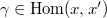 . Notice the category of representations of
. Notice the category of representations of 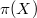 is equivalent to the category of finite etale coverings of
is equivalent to the category of finite etale coverings of  .
.
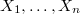 be smooth schemes of finite type over a finite field
be smooth schemes of finite type over a finite field 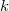 . Let
. Let 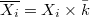 . Let
. Let 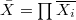 . Let
. Let 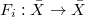 be the
be the 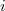 -th partial Frobenius morphism
-th partial Frobenius morphism 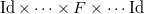 . Then
. Then
- let
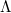 be a local system over
be a local system over 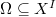 open dense, equipped with isomorphism
open dense, equipped with isomorphism 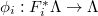 over
over 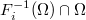 such that
such that 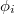 commute and
commute and 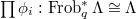 is the canonical isomorphism. Then there exists an
is the canonical isomorphism. Then there exists an 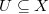 open dense such that
open dense such that 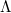 extends a local system to
extends a local system to 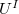 .
. - we have an equivalence
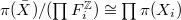 : namely, a representation of
: namely, a representation of 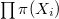 is the same as a finite etale covering
is the same as a finite etale covering 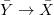 plus compatible isomorphisms
plus compatible isomorphisms 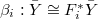 .
.
- Assume
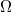 is the largest subset of
is the largest subset of 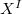 to which
to which 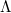 extends. Let
extends. Let 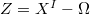 . Then
. Then 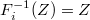 for all
for all 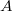 . Say
. Say 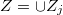 is a union of irreducible components. We will show that each
is a union of irreducible components. We will show that each 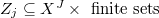 for some
for some 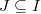 ,
, 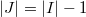 .
.
- First assume that
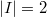 . Let
. Let 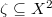 be an irreducible divisor. Let
be an irreducible divisor. Let 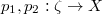 be the two projections. Suppose otherwise both projections are surjective. Let
be the two projections. Suppose otherwise both projections are surjective. Let 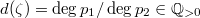 . Then
. Then 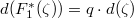 . But
. But 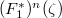 is finite (only finitely many component), a contradiction. So every component of
is finite (only finitely many component), a contradiction. So every component of 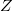 is either horizontal or vertical.
is either horizontal or vertical. - For general
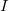 , let
, let 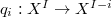 . Let
. Let 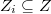 be the maximal subset such that
be the maximal subset such that 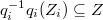 . Then
. Then 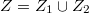 by the previous case. We may then replace
by the previous case. We may then replace 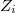 by their subsets of pure codimension 1. Hence
by their subsets of pure codimension 1. Hence 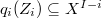 is closed of pure codimension 1 and invariant under the remaining partial Frobenius. Then we induct on
is closed of pure codimension 1 and invariant under the remaining partial Frobenius. Then we induct on  to prove the claim.
to prove the claim.
- First assume that
- For simplicity let us assume all
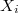 's in the theorem are the same. Let
's in the theorem are the same. Let 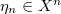 be the geometric generic point. Now we apply Corollary 2 to
be the geometric generic point. Now we apply Corollary 2 to 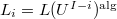 , we know for each
, we know for each 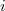 the finite etale cover
the finite etale cover 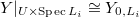 for some
for some 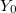 . Thus
. Thus 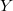 factors through
factors through 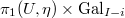 for each
for each 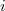 , hence factors through their intersection
, hence factors through their intersection 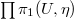 by part a).
¡õ
by part a).
¡õ
04/26/2016
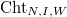 directly, the action of
directly, the action of 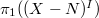 on
on 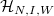 does extend to an action of
does extend to an action of 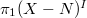 . In fact, the first partial Frobenius
. In fact, the first partial Frobenius 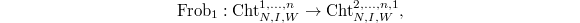 which lies over the map
which lies over the map 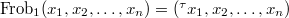 . Because the cohomology
. Because the cohomology 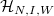 does not depend on the partition of
does not depend on the partition of 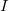 and the partial Frobenius induces an isomorphism of etale sites, we know that the
and the partial Frobenius induces an isomorphism of etale sites, we know that the 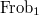 induces an automorphism
induces an automorphism  (it increases
(it increases 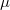 but does not effect the Hecke finite classes). The composition of the
but does not effect the Hecke finite classes). The composition of the  permutation
permutation 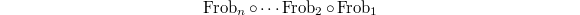 maps
maps 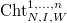 to itself, and is exactly the absolute Frobenius. Since
to itself, and is exactly the absolute Frobenius. Since 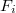 covers
covers 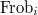 on
on 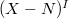 , commutes with each other and
, commutes with each other and 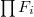 is the absolute Frobenius, by Theorem 16 we know that the action of
is the absolute Frobenius, by Theorem 16 we know that the action of 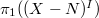 extends to an action of
extends to an action of 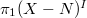 .
.
 Compatibility of excursion operators and Hecke operators
Compatibility of excursion operators and Hecke operators
We now come to the last key point of this course, i.e., item e) in Theorem 4), which is Lemma 10.2/Prop. 6.2 in V. Lafforgue's paper:
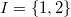 ,
, 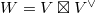 an irreducible representation of
an irreducible representation of 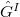 . Let
. Let 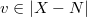 . Let
. Let 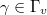 have degree
have degree 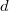 under
under 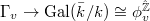 . Then
. Then 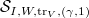 depends only on
depends only on 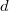 . In particular, the inertia
. In particular, the inertia 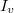 acts trivially. Moreover, if
acts trivially. Moreover, if 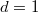 , then
, then 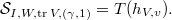
Here is a rough strategy. Consider the Deligne-Mumford stack 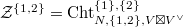 over
over 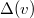 . Then one constructs two closed substack
. Then one constructs two closed substack 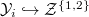 (
(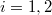 ) and together with morphisms
) and together with morphisms 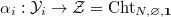 such that
such that
- The first two stages of the excursion operator (creation and
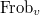 ) is realized by a cohomological correspondence supported on
) is realized by a cohomological correspondence supported on 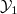 (after normalizing by a half-integral power of
(after normalizing by a half-integral power of 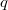 ).
). - The last stage (annihilation) is realized by a cohomological correspondence supported on
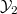 . Thus
. Thus 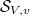 is a cohomological correspondence supported on
is a cohomological correspondence supported on 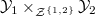 . Now:
. Now: - The fiber product
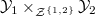 is the usual etale Hecke correspondence
is the usual etale Hecke correspondence 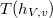 ,
, 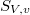 equals to this fiber product.
equals to this fiber product.
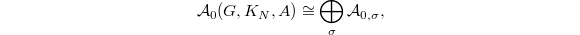 where
where 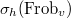 corresponds to
corresponds to 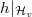 under the Satake isomorphism.
under the Satake isomorphism.
![$[m]\hookrightarrow [m+1]$](./latex/VincentLafforgue/latex2png-VincentLafforgue_138417622_-5.gif) .
.
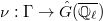 .
.
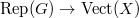 .
.
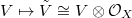 .
.
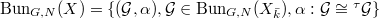 .
.
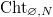 , the moduli of shtukas with no paws.
, the moduli of shtukas with no paws.
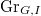 is represented by an ind-scheme, ind-projective and of finite type over
is represented by an ind-scheme, ind-projective and of finite type over  is smooth of dimension equal to
is smooth of dimension equal to 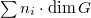 .
.
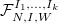 over
over 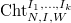 . More generally, we define
. More generally, we define 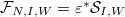 .
.