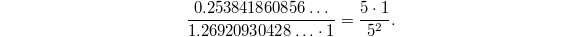These are notes prepared for a talk in the Student Mathematics Colloquium at Columbia, Fall 2018. We explain the monstrous moonshine, and recent new moonshine for O'Nan group and its connection with the BSD conjecture due to Duncan—Mertens—Ono. Our main references are [1],[2],[3], [4], [5] and [6].
 Elliptic curves and modular functions
Elliptic curves and modular functions
An elliptic curve  over
over  is a smooth cubic curve of the form
is a smooth cubic curve of the form 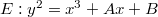 , where
, where 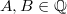 . The change of variable
. The change of variable 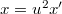 ,
, 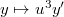 preserves the form of the equation and gives an elliptic curve
preserves the form of the equation and gives an elliptic curve 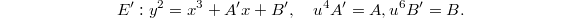 Then
Then 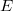 and
and 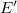 are isomorphic over the field
are isomorphic over the field 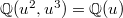 .
.
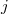 -invariant of
-invariant of 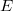 to be
to be 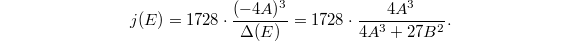 Then we see that
Then we see that 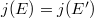 . Conversely if
. Conversely if 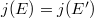 , then
, then 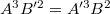 , and we may find some
, and we may find some 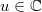 (actually
(actually 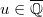 ) satisfying the desired transformation.
) satisfying the desired transformation.
In summary, we may classify elliptic curves over 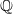 as follows.
as follows.
- The isomorphism class of elliptic curve
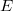 over
over 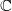 (or
(or 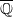 ) is determined by
) is determined by 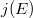 .
. - If
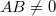 , then there is a unique elliptic curve
, then there is a unique elliptic curve 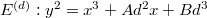 over
over 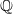 that is isomorphic to
that is isomorphic to 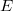 over
over 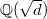 but not over
but not over 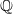 . We call
. We call 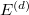 the
the 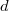 -quadratic twist of
-quadratic twist of 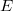 .
.
There is also an analytic classification of elliptic curves over 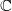 . Given any
. Given any  in the upper half plane
in the upper half plane 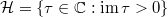 , we have the associated elliptic curve
, we have the associated elliptic curve 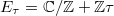 . Then
. Then 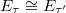 if and only if
if and only if 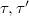 lies in the same
lies in the same 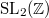 -orbit. Therefore the
-orbit. Therefore the 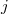 -invariant induces a function
-invariant induces a function 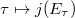 on the upper half plane that is invariant under
on the upper half plane that is invariant under 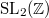
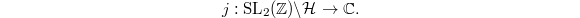 This is a first example of a modular function (a function with a large group of symmetry given by the modular group
This is a first example of a modular function (a function with a large group of symmetry given by the modular group 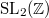 ). Using the Weierstrass
). Using the Weierstrass 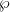 -function one can write down the coefficients
-function one can write down the coefficients 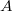 ,
, 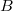 as functions of
as functions of  , using Eisenstein series of weight 4 and 6,
, using Eisenstein series of weight 4 and 6, 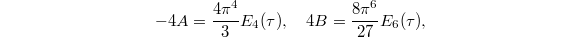 where
where 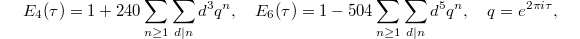 and
and 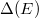 as Ramanujan's cusp form of weight 12,
as Ramanujan's cusp form of weight 12, 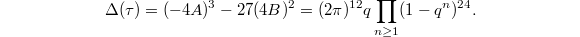 In this way we obtain a nice analytic expression of the
In this way we obtain a nice analytic expression of the  -invariant,
-invariant, 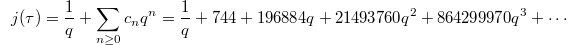 Notice the appearance of
Notice the appearance of 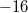 and 1728 in the definition of
and 1728 in the definition of 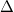 and
and 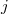 normalizes their leading coefficients to be
normalizes their leading coefficients to be 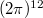 and 1 respectively.
and 1 respectively.
The 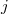 -invariant is an example of a Hauptmodul (principal modular function), as the modular curve
-invariant is an example of a Hauptmodul (principal modular function), as the modular curve 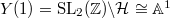 , and the compactified modular curve
, and the compactified modular curve 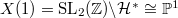 is of genus 0 with
is of genus 0 with 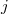 a generator of its function field. More generally can can consider quotient by other arithmetic subgroups of
a generator of its function field. More generally can can consider quotient by other arithmetic subgroups of 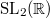 such as
such as 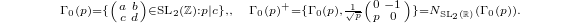
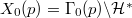 has genus 0 exactly when
has genus 0 exactly when 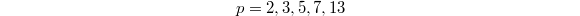 (the missing prime
(the missing prime 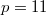 corresponds to the elliptic curve over
corresponds to the elliptic curve over 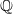 with smallest conductor
with smallest conductor 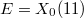 ).
).
The curve 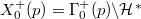 has genus 0 exactly for the following 15 primes
has genus 0 exactly for the following 15 primes 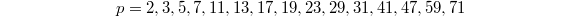 (the missing primes
(the missing primes 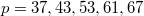 all correspond to elliptic curves).
all correspond to elliptic curves).
 such that all supersingular elliptic curves are defined over
such that all supersingular elliptic curves are defined over 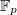 (rather than over
(rather than over 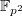 ), by looking at the geometry of
), by looking at the geometry of 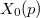 modulo
modulo 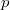 and the action of the Atkin—Lehner involution
and the action of the Atkin—Lehner involution 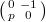 .
.
 Monstrous Moonshine
Monstrous Moonshine
The origin of the mathematical terminology moonshine here is the figurative use of the word as foolish talks or ideas (dates back to 15th century: "moonshine in water"), rather than its later use as smuggled alcohol (in 18th century). The "foolish" connection starts with the completely different story of the classification of finite simple groups. Now we know that a finite simple group belongs to one of:
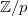 ,
,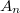 ,
,- 16 infinite families of finite groups of Lie type (such as
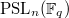 ),
), - 26 sporadic groups.
The largest sporadic group is known as the monster group 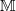 , due to its monstrous size and complexity. It has order
, due to its monstrous size and complexity. It has order 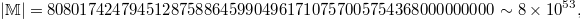 and has 194 conjugacy classes. The existence of
and has 194 conjugacy classes. The existence of 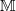 was first predicted by Fischer and Griess in 1973, and Griess gave a quite complicated construction in 1980, as the group of linear transformations on a huge vector space (of dimension 196883!) that preserve a certain commutative but nonassociative bilinear product, now known as the Griess product. A total of 20 sporadic groups appear as subquotients of
was first predicted by Fischer and Griess in 1973, and Griess gave a quite complicated construction in 1980, as the group of linear transformations on a huge vector space (of dimension 196883!) that preserve a certain commutative but nonassociative bilinear product, now known as the Griess product. A total of 20 sporadic groups appear as subquotients of 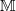 , known as the happy family, and the remaining 6 sporadic group are known as pariah (low class of southern India) groups, including the Lyons group, Janko groups
, known as the happy family, and the remaining 6 sporadic group are known as pariah (low class of southern India) groups, including the Lyons group, Janko groups 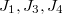 , Rudvalis group, and O'Nan group.
, Rudvalis group, and O'Nan group.
The first surprise comes from Ogg's observation that 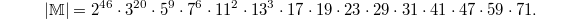 The prime factors are exactly those
The prime factors are exactly those 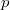 such that
such that 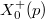 with a Hauptmodul! A "moonshine" idea as it may appear to be simply a coincidence of small numbers.
with a Hauptmodul! A "moonshine" idea as it may appear to be simply a coincidence of small numbers.
The second surprise comes from the character table of 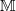 . Even before the rigorous construction of
. Even before the rigorous construction of 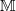 , Fischer—Livingstone—Thorne computed the character table of
, Fischer—Livingstone—Thorne computed the character table of 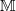 in 1978 assuming its existence. The dimension of the representation are quite large, here is the character values of the conjugacy class 1A (trivial) and 2B (order 2) of the first four representations, copied from the ATLAS of finite groups:
in 1978 assuming its existence. The dimension of the representation are quite large, here is the character values of the conjugacy class 1A (trivial) and 2B (order 2) of the first four representations, copied from the ATLAS of finite groups:
![\begin{center}
\begin{tabular}[h]{|c|c|c|}
$\chi$ & 1A & 2B\\\hline
$\chi_1$ &1 & 1\\
$\chi_2$ &196883 & 275\\
$\chi_3$ &21296876 & -2324\\
$\chi_4$ & 842609326 & 12974
\end{tabular}
\end{center}](./latex/Moonshine/latex2png-Moonshine_137477174_.gif)
Now observe the remarkable coincidence (due to McKay and Thompson):
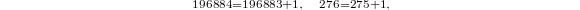
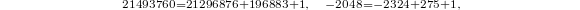
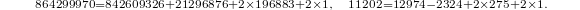 In other words, the first four coefficients in
In other words, the first four coefficients in 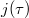 and
and 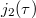 exactly matches the character values of the representation
exactly matches the character values of the representation 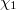 ,
, 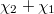 ,
, 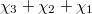 ,
, 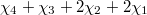 on the conjugacy 1A and 2B respectively, which can no longer be the law of small numbers! This leads to the following monstrous moonshine conjecture due to Thompson and Conway—Norton.
on the conjugacy 1A and 2B respectively, which can no longer be the law of small numbers! This leads to the following monstrous moonshine conjecture due to Thompson and Conway—Norton.
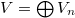 such that for any
such that for any 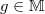 the Mckay—Thompson series
the Mckay—Thompson series 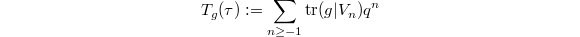 is a Hauptmodul for a discrete subgroup
is a Hauptmodul for a discrete subgroup 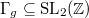 of genus 0.
of genus 0.
In fact Conway—Norton gave an explicit recipe for the subgroup 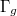 , which lies between
, which lies between 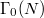 and its normalizer for some
and its normalizer for some 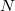 . Thus the monstrous moonshine provides a natural explanation of Ogg's observation on the order of
. Thus the monstrous moonshine provides a natural explanation of Ogg's observation on the order of 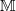 .
.
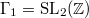 ,
, 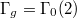 for
for 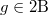 as suggested by the data above. We have
as suggested by the data above. We have 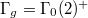 for
for 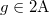 and the Hauptmodul corresponding to 2A is given by
and the Hauptmodul corresponding to 2A is given by 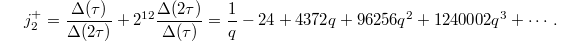
The moonshine module 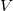 was constructed by Frenkel—Lepowsky—Meurman in 1983 which has a rich structure of a vertex operator algebra (whose automorphism group being
was constructed by Frenkel—Lepowsky—Meurman in 1983 which has a rich structure of a vertex operator algebra (whose automorphism group being 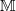 ), and they verified the conjecture for
), and they verified the conjecture for 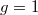 . The full monstrous moonshine conjecture was later proved by Borcherds.
. The full monstrous moonshine conjecture was later proved by Borcherds.
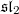 and 3-dimensional Heisenberg algebras), and the construction of the monster Lie algebra from the moonshine module. The key is to prove certain recursive relations of the McKay—Thompson series for
and 3-dimensional Heisenberg algebras), and the construction of the monster Lie algebra from the moonshine module. The key is to prove certain recursive relations of the McKay—Thompson series for 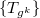 and reduce the conjecture to a small finite number of identities (the first 7 terms) checkable by hand. The recursive relation finally boils down to the denominator identity for the monster Lie algebra (generalizing the classical Weyl denominator formula for Lie algebras).
and reduce the conjecture to a small finite number of identities (the first 7 terms) checkable by hand. The recursive relation finally boils down to the denominator identity for the monster Lie algebra (generalizing the classical Weyl denominator formula for Lie algebras).
 O'Nan moonshine
O'Nan moonshine
Much work has since been done on the moonshine for other groups in the happy family, which relates the character values of a sporadic group to Hauptmodul of genus 0. For example the Hauptmodul 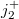 gives the dimension of the irreducible representations of the baby monster group
gives the dimension of the irreducible representations of the baby monster group  (the second largest sporadic). However, there has been no interesting genus 0 moonshine for the remaining six pariah groups. Recently, progress has been made by Duncan—Mertens—Ono on one of the pariah groups, the O'Nan group
(the second largest sporadic). However, there has been no interesting genus 0 moonshine for the remaining six pariah groups. Recently, progress has been made by Duncan—Mertens—Ono on one of the pariah groups, the O'Nan group  . It has size
. It has size 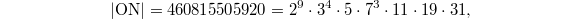 and has 30 conjugacy classes. This new O'Nan moonshine has a different flavor: the McKay—Thompson series involve weight 3/2 modular forms, rather than Hauptmoduls (weight 0 modular forms).
and has 30 conjugacy classes. This new O'Nan moonshine has a different flavor: the McKay—Thompson series involve weight 3/2 modular forms, rather than Hauptmoduls (weight 0 modular forms).
 -module
-module 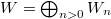 , where
, where 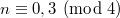 , such that for each
, such that for each 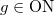 , the McKay—Thompson series
, the McKay—Thompson series 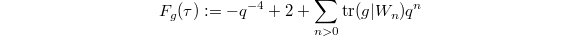 is a weakly holomorphic modular form of weight 3/2 on
is a weakly holomorphic modular form of weight 3/2 on 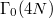 , where
, where 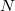 is the order of
is the order of 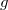 .
.
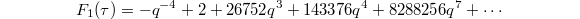 a generating series of traces of singular of moduli which dates back to Zagier (2002), where
a generating series of traces of singular of moduli which dates back to Zagier (2002), where 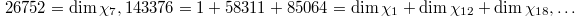
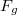 . To relate it to O'Nan, one checks the first few coefficients of these explicit modular forms agree with the desired traces and deduce the rest using the Schur orthogonal relations for characters and certain congruence relations built into the construction of
. To relate it to O'Nan, one checks the first few coefficients of these explicit modular forms agree with the desired traces and deduce the rest using the Schur orthogonal relations for characters and certain congruence relations built into the construction of 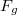 . A natural interesting question is whether one can find more intrinsic definition of the moonshine module
. A natural interesting question is whether one can find more intrinsic definition of the moonshine module 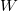 independent of the explicit constructions of
independent of the explicit constructions of 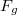 (e.g., using vertex operator algebras).
(e.g., using vertex operator algebras).
A new feature in the O'Nan moonshine is that the modular forms are of weight 3/2, which encodes even richer arithmetic. It leads to an intriguing relation with the BSD conjecture which we now briefly describe.
 Connection with BSD
Connection with BSD
Come back to the elliptic curve 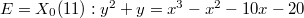 (or in Weierstrass form
(or in Weierstrass form 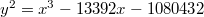 ). It has an associated weight 2modular form
). It has an associated weight 2modular form
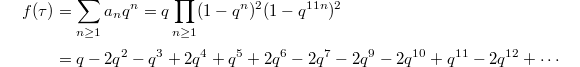 such that the coefficient
such that the coefficient 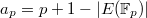 encodes the number of solution of
encodes the number of solution of 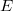 mod
mod 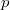 (when
(when 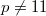 ).
).
More generally, the modularity theorem associates a weight 2 modular form 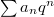 to any elliptic curve
to any elliptic curve 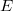 over
over 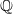 . Analogous to the Riemann zeta function, we define the
. Analogous to the Riemann zeta function, we define the 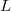 -function of
-function of 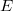 to be
to be 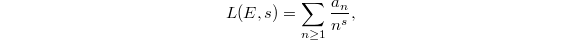 which has analytic continuation to all of
which has analytic continuation to all of  and satisfies a functional equation relating
and satisfies a functional equation relating  and
and 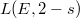 .
.
The rank part is known when 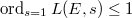 due to Gross—Zagier and Kolyvagin in 1980's. Regarding the BSD formula, here is a more recent theorem.
due to Gross—Zagier and Kolyvagin in 1980's. Regarding the BSD formula, here is a more recent theorem.
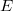 satisfying some assumptions, there are infinitely many quadratic twists
satisfying some assumptions, there are infinitely many quadratic twists 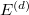 of rank 0 such that the BSD formula holds for
of rank 0 such that the BSD formula holds for 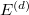 .
.
However, the truth for of BSD formula for all twists is still not known, even for 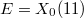 (the problem comes from the 11-part and 2-part of the BSD formula).
(the problem comes from the 11-part and 2-part of the BSD formula).
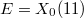 . Let
. Let  be a fundamental discriminant that is not a square mod 11. Assume (the 11-part of) the BSD formula holds for
be a fundamental discriminant that is not a square mod 11. Assume (the 11-part of) the BSD formula holds for 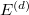 . Then the followings are equivalent:
. Then the followings are equivalent:
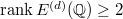 or
or ![$\Sha(E^{(d)})[ 11 ]\ne0$](./latex/Moonshine/latex2png-Moonshine_93041879_-5.gif) .
.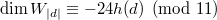 . Here
. Here 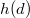 is the class number of
is the class number of 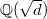 .
.
Similar results hold for 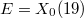 and
and 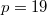 .
.
So the O'Nan group knows about solving cubic equations! Naturally one wonders if one can check the second condition in terms of the O'Nan group more intrinsically, which would imply important consequences on the arithmetic of 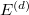 .
.
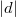 -th coefficient of a weight 3/2 form associated to
-th coefficient of a weight 3/2 form associated to 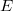 to
to 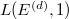 , and a celebrated theorem of Zagier shows that the generating series of (Hurwitz) class numbers and more generally generating series of traces of singular moduli are (mock) modular forms of weight 3/2. The theorem then follows by writing
, and a celebrated theorem of Zagier shows that the generating series of (Hurwitz) class numbers and more generally generating series of traces of singular moduli are (mock) modular forms of weight 3/2. The theorem then follows by writing 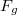 (
(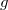 of order 11) as an explicit linear combination of weight 3/2 modular forms of Waldspurger's type and Zagier's type and using the congruence between
of order 11) as an explicit linear combination of weight 3/2 modular forms of Waldspurger's type and Zagier's type and using the congruence between 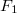 and
and 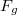 mod 11.
mod 11.
References
[1]Monstrous moonshine, Bull. London Math. Soc. 11 (1979), no.3, 308--339.
[2]Introduction to the Monster Lie algebra, Groups, combinatorics \& geometry (Durham, 1990), London Math. Soc. Lecture Note Ser., 165 Cambridge Univ. Press, Cambridge, 1992, 99--107.
[3]What is Moonshine?, Proceedings of the International Congress of Mathematicians, Vol. I (Berlin, 1998), 1998, 607--615.
[4]Monstrous moonshine: the first twenty-five years, Bull. London Math. Soc. 38 (2006), no.1, 1--33.
[5]Pariah moonshine, Nature communications 8 (2017), no.1, 670.
[6]O'Nan moonshine and arithmetic, arXiv e-prints (2017), arXiv:1702.03516.
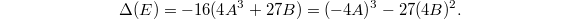 Then
Then 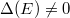 .
.
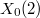 is given by
is given by 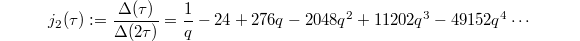
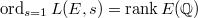 .
.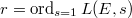 , then
, then 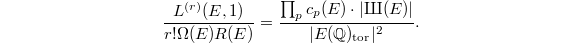
 and the BSD formula holds:
and the BSD formula holds: