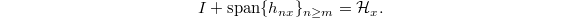These are expanded notes prepared for a talk in Arbeitsgemeinschaft: Higher Gross Zagier Formulas held at Oberwolfach, Spring 2017, on Yun-Zhang's beautiful work [1]. This is the last one in a series of 17 talks.
You may also want to check out Tony Feng's excellent notes of all talks and my earlier course notes.
 Overview
Overview
Our goal today is to finish the proof of the main identity 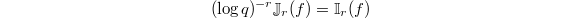 for all functions in the spherical Hecke algebra
for all functions in the spherical Hecke algebra 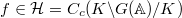 of
of 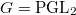 . For any
. For any 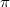 (unramified everywhere) cuspidal automorphic representation of
(unramified everywhere) cuspidal automorphic representation of 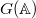 , the LHS via the analytic spectral decomposition and the RHS via the cohomological spectral decomposition (discussed below) would imply the identity
, the LHS via the analytic spectral decomposition and the RHS via the cohomological spectral decomposition (discussed below) would imply the identity ![$$\lambda_\pi(f)\cdot \mathcal{L}^{(r)}(\pi_{F'}, 1/2)\sim \langle [\Sht_T]_\pi, f*[\Sht_T]_\pi\rangle.$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_265215828_.gif) We now have the wonderful opportunity to apply the identity to simplest element in the Hecke algebra, namely the the unit element
We now have the wonderful opportunity to apply the identity to simplest element in the Hecke algebra, namely the the unit element 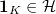 , and obtain our desired Higher Gross—Zagier formula
, and obtain our desired Higher Gross—Zagier formula ![$$\mathcal{L}^{(r)}(\pi_{F'}, 1/2)\sim\langle [\Sht_T]_\pi, [\Sht_T]_\pi\rangle.$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_4690413_.gif)
Ana's talk has proved the main identity for many 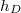 's but we fall short of proving it for the element
's but we fall short of proving it for the element 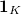 : in some sense the simplest Hecke function gives the most difficult situation for intersection computation (self-intersection), and considering
: in some sense the simplest Hecke function gives the most difficult situation for intersection computation (self-intersection), and considering 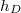 for sufficiently large
for sufficiently large 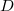 allows us to move away from the self-intersection situation and make the computation easier. What we would like to do is to resolve this tension, and deduce the identity for all Hecke functions from sufficiently many
allows us to move away from the self-intersection situation and make the computation easier. What we would like to do is to resolve this tension, and deduce the identity for all Hecke functions from sufficiently many 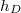 's by just doing commutative algebra. What make the deduction possible are certain key finiteness properties of the Hecke action on the middle cohomology of the moduli of shtukas.
's by just doing commutative algebra. What make the deduction possible are certain key finiteness properties of the Hecke action on the middle cohomology of the moduli of shtukas.
 Key finiteness theorems
Key finiteness theorems
Recall the middle cohomology 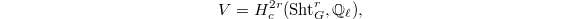 which admits an action of the Hecke algebra
which admits an action of the Hecke algebra 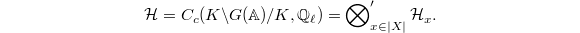
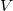 is infinite dimensional caused by the fact that
is infinite dimensional caused by the fact that 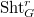 is only locally of finite type. This infinite dimensionality can already be seen when
is only locally of finite type. This infinite dimensionality can already be seen when 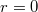 , where we recover the classical Hecke action on the space of automorphic forms of level 1:
, where we recover the classical Hecke action on the space of automorphic forms of level 1: 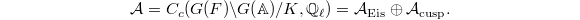 Here the space of cusp forms
Here the space of cusp forms 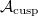 is finite dimensional, but the space of Eisenstein series is infinite dimensional.
is finite dimensional, but the space of Eisenstein series is infinite dimensional.
To kill the Eisenstein part, we again make use of the Eisenstein ideal appeared in Ilya's talk on analytic spectral decomposition. Recall we define the Eisenstein ideal to be ![$$I_\mathrm{Eis}:=\ker(\mathcal{H}\xrightarrow{\mathrm{Sat}} \mathcal{H}_{A}\cong \mathbb{Q}_\ell[\Div_X(k)]\rightarrow \mathbb{Q}_\ell[\Pic_X(k)]),$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_65853425_.gif) moreover
moreover ![$\mathcal{H}/I_\mathrm{Eis}\cong \mathbb{Q}_\ell[\Pic_X(k)]^{\iota}$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_137043634_-5.gif) , which is 1-dimensional as a ring (
, which is 1-dimensional as a ring (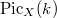 is an extension of
is an extension of 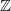 by the finite group
by the finite group 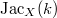 ).
).
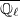 -point of
-point of 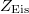 factors as
factors as ![$$\mathcal{H}\rightarrow \mathbb{Q}_\ell[\Pic_X(k)]\xrightarrow{\chi} \overline{\mathbb{Q}_\ell}$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_168703023_.gif) for some character
for some character 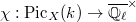 . In particular ,
. In particular , 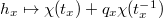 . When
. When 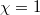 , we get
, we get 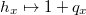 . This is completely analogous to classical Eisenstein ideal
. This is completely analogous to classical Eisenstein ideal 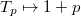 (=
(=  -th Fourier coefficient of the ``weight 2'' Eisenstein series), which was invented by B. Mazur to study rational points on modular curves and torsion points on elliptic curves.
-th Fourier coefficient of the ``weight 2'' Eisenstein series), which was invented by B. Mazur to study rational points on modular curves and torsion points on elliptic curves.
After killing the Eisenstein part, we indeed obtain a finite dimensional vector space.
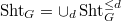 is a union of open substacks of finite type
is a union of open substacks of finite type 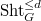 with instability index bounded by
with instability index bounded by 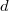 . The key point here is that one can understand the difference between the cohomology of
. The key point here is that one can understand the difference between the cohomology of 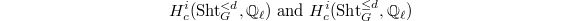 using horocycles discussed in Lizao's talk. More precisely, when
using horocycles discussed in Lizao's talk. More precisely, when 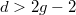 , the cone of the natural map
, the cone of the natural map 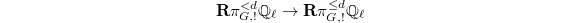 is equal to
is equal to $](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_91777997_-7.gif) , which is a local system concentrated in degree
, which is a local system concentrated in degree  . Here
. Here 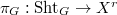 ,
, 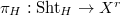 , and
, and 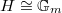 is the quotient torus of the Borel of
is the quotient torus of the Borel of 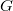 .
.
In particular, it suffices to work with the generic fiber and show 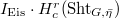 is finite dimensional. Let
is finite dimensional. Let 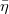 be the geometric generic fiber of
be the geometric generic fiber of  , then the map
, then the map 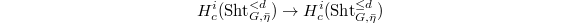 is an isomorphism when
is an isomorphism when 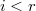 and injective when
and injective when 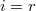 with cokernel
with cokernel 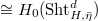 .
.
Let 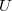 be the finite union of
be the finite union of 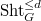 , where instability index
, where instability index 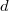 is not all
is not all 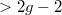 . Using the compatibility of the cohomological constant map and the Satake transform, we have a commutative diagram
. Using the compatibility of the cohomological constant map and the Satake transform, we have a commutative diagram ![$$\xymatrix{H^r_c(\Sht_{G,\bar\eta}) \ar[r]^{f*} \ar[d]^{\prod \gamma_d}& H^r_c(\Sht_{G,\bar\eta}) \ar[r] \ar[d]^{\prod \gamma_d} & H^r_c(\Sht_{G,\bar \eta})/H^r_c(U_{\bar \eta}) \ar[d]^{\prod\limits_{d>2g-2} \gamma_d} \\ \prod_{d} H_0(\Sht_{H,\bar \eta}^d) \ar[r]^{\mathrm{Sat}(f)*} & \prod_{d} H_0(\Sht_{H,\bar \eta}^d) \ar[r] & \prod_{d>2g-2} H_0(\Sht^d_{H,\bar \eta})}$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_15239746_.gif) For
For 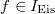 , by definition
, by definition 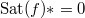 and so the bottom row is zero. The cohomological constant map on the right is injective since
and so the bottom row is zero. The cohomological constant map on the right is injective since 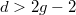 . It follows that the top row is zero, and hence the image of
. It follows that the top row is zero, and hence the image of 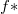 is contained in
is contained in 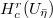 , which is finite dimensional as desired.
¡õ
, which is finite dimensional as desired.
¡õ
Using a similar argument, one can also prove the following finiteness theorem.
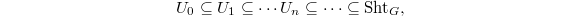 Define the images
Define the images 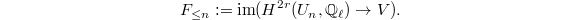 Suppose the cohomological correspondence
Suppose the cohomological correspondence 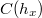 induced by
induced by 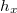 sends
sends 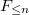 to
to 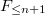 , then we have the induced map on associated graded
, then we have the induced map on associated graded 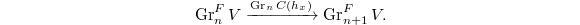 It turns out one can construct such sequence
It turns out one can construct such sequence 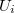 such that these induced maps
such that these induced maps 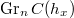 are surjective for all
are surjective for all 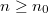 for some
for some 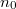 . The result then follows since
. The result then follows since 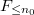 is finite dimensional.
is finite dimensional.
The key point here again is by the compatibility of Satake isomorphism and the cohomological constant term, the 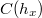 -action on the cokernel can be made explicit as
-action on the cokernel can be made explicit as 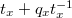 -action. One can then choose
-action. One can then choose 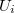 appropriately so that
appropriately so that 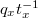 acts trivially on the cokernels for degree reasons and to make sure that
acts trivially on the cokernels for degree reasons and to make sure that 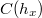 induces a surjection
induces a surjection 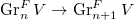 .
¡õ
.
¡õ
 Cohomological spectral decomposition
Cohomological spectral decomposition
Let ![$\overline{\mathcal{H}}=\im (\mathcal{H}\rightarrow\End_{\mathbb{Q}_\ell}(V)\times \mathbb{Q}_\ell[\Pic_X(k)])$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_125641713_-5.gif) . We have the following immediate consequence:
. We have the following immediate consequence:
![$$\overline{\mathcal{H}}\hookrightarrow \End_{\mathcal{H}_x}(V \oplus \mathbb{Q}_\ell[\Pic_X(k)]^\iota).$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_265438427_.gif) By Theorem 2,
By Theorem 2, 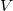 is a finite
is a finite 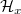 -module. Also
-module. Also ![$\mathbb{Q}_\ell[\Pic_X(k)]^\iota$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_41619501_-5.gif) is finite
is finite 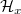 -module (due to the finiteness of
-module (due to the finiteness of 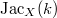 ). It follows that RHS is a finite
). It follows that RHS is a finite 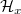 -module and hence
-module and hence 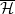 is a finite
is a finite 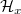 -module. Because
-module. Because ![$\mathcal{H}_x\cong \mathbb{Q}_\ell[h_x]$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_41925929_-5.gif) is a polynomial algebra, it follows that
is a polynomial algebra, it follows that 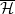 is a finitely generated
is a finitely generated 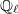 -algebra.
¡õ
-algebra.
¡õ
Now 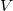 is a finite module over the noetherian ring
is a finite module over the noetherian ring 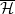 (by Theorem 2,
(by Theorem 2, 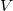 is a finite module even over
is a finite module even over 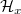 ), we obtain the following cohomological spectral decomposition:
), we obtain the following cohomological spectral decomposition:
- There is a decomposition
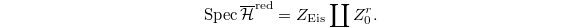 Here
Here 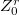 is a finite set of closed points.
is a finite set of closed points. - There is a unique decomposition of
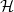 -modules
-modules 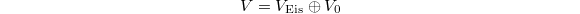 such that
such that 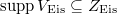 ,
, 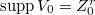 and
and 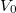 is finite dimensional over
is finite dimensional over 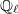 .
.
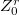 is a finite set of closed points and
is a finite set of closed points and 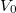 is finite dimensional follows from Theorem 1.
is finite dimensional follows from Theorem 1.
 Finish of the proof of the main identity
Finish of the proof of the main identity
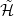 to be the image of
to be the image of 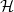 in
in 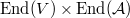 . Then both sides of the identify only depend on the image of
. Then both sides of the identify only depend on the image of 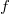 in
in 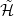 . Define
. Define 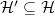 to be the linear subspace spanned by
to be the linear subspace spanned by 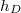 's, where
's, where 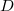 effective divisor of degree
effective divisor of degree 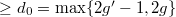 . By Ana's Talk, we already proved the identity for
. By Ana's Talk, we already proved the identity for 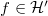 . So it remains to show that the composition
. So it remains to show that the composition 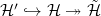 is surjective.
is surjective.
Using the key finiteness theorem one can prove the following lemma:
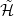 is a finitely generated
is a finitely generated 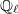 -algebra, so there exists a finite set
-algebra, so there exists a finite set 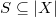 such that the images of
such that the images of 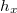 (
(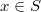 ) generate
) generate 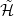 as
as 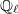 -algebra. Enlarge
-algebra. Enlarge 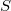 so that
so that 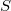 also contains all
also contains all 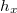 for
for 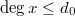 . Let
. Let 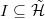 be the ideal generated by the images of
be the ideal generated by the images of 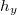 (
(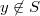 ), then
), then 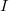 works.
works.
In fact, because 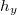 is away from the generating set
is away from the generating set 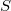 , we have
, we have 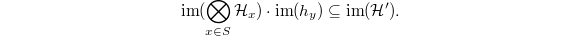 Since the left-hand-side is equal to
Since the left-hand-side is equal to 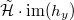 spans
spans 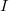 by definition, we know
by definition, we know 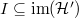 (think:
(think: 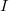 is ``small'' enough).
is ``small'' enough).
On the other hand, by the cohomological spectral decomposition (Theorem 3), 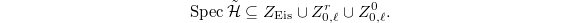 It remains to rule out the Eisenstein part: i.e., to show that
It remains to rule out the Eisenstein part: i.e., to show that 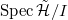 is disjoint from
is disjoint from 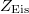 . Suppose
. Suppose 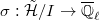 is a
is a 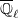 -point of
-point of 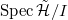 lies in
lies in 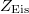 . Then
. Then 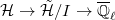 factors as
factors as ![$$\mathcal{H}\rightarrow \mathbb{Q}[\Pic_X(k)]\xrightarrow{\chi} \overline{\mathbb{Q}}_\ell,$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_110900762_.gif) for some character
for some character 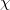 . It follows that for
. It follows that for 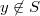 , we have
, we have 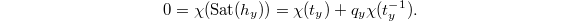 Hence
Hence 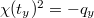 . Let
. Let 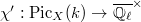 be the character
be the character 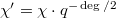 . Then
. Then 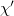 has finite image and
has finite image and 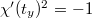 . By class field theory
. By class field theory 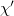 can be identified as a Galois character of
can be identified as a Galois character of 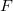 and hence
and hence 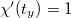 for infinitely many
for infinitely many 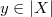 by Chebotarev density. This contradicts
by Chebotarev density. This contradicts 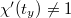 for all
for all 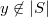 . So
. So 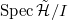 is disjoint from
is disjoint from 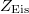 and hence
and hence 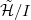 is finite dimensional (think:
is finite dimensional (think: 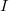 is ``large'' enough).
¡õ
is ``large'' enough).
¡õ
Besides the key finiteness theorems, we need one additional ingredient concerning the local Hecke algebra. It is a bit magical but completely elementary:
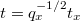 . Then under the Satake transform we may identify
. Then under the Satake transform we may identify 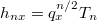 , where
, where 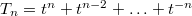 . Note that
. Note that 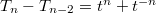 , thus it suffices to show that for any nonzero ideal
, thus it suffices to show that for any nonzero ideal 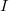 in the ring
in the ring ![$\mathbb{Q}[(t+t^{-1})]$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_85834214_-5.gif) of symmetric polynomials in
of symmetric polynomials in 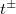 , and any
, and any 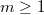 , we have
, we have ![$$I+\mathrm{span}\{t^n+t^{-n}\}_{n\ge m}= \mathbb{Q}[(t+t^{-1})].$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_63745525_.gif) For any
For any ![$g\in \mathbb{Q}[(t+t^{-1})]$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_170071528_-5.gif) , write
, write 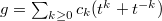 (
(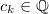 ). We define the lowest degree of
). We define the lowest degree of 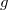 to be the smallest
to be the smallest 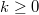 such that
such that 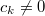 . Then it suffices to show that for any given
. Then it suffices to show that for any given 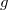 , we can find an element
, we can find an element 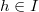 with same the lowest degree as that of
with same the lowest degree as that of 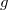 . Since
. Since ![$\mathbb{Q}[(t+t^{-1})]$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_85834214_-5.gif) is a PID, we may assume
is a PID, we may assume 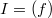 for some
for some ![$f\in \mathbb{Q}[(t+t^{-1})]$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_153294312_-5.gif) . Notice that for any
. Notice that for any 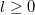 , there is no cancellation in the product
, there is no cancellation in the product 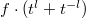 , and so one can always choose some
, and so one can always choose some 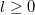 such that
such that 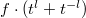 has a prescribed lowest degree (in particular, the lowest degree of
has a prescribed lowest degree (in particular, the lowest degree of 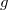 ) as desired.
¡õ
) as desired.
¡õ
Now we can finish the proof of the main identity using the previous two lemmas. For any 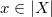 , look at the commutative diagram
, look at the commutative diagram ![$$\xymatrix{\mathcal{H}' \ar[r] &\mathcal{H} \ar[r] &\tilde{\mathcal{H}} \ar[r] & \tilde{\mathcal{H}}/I\\ \mathcal{H}'\cap \mathcal{H}_x \ar[u] \ar[r] & \mathcal{H}_x \ar[u]\ar[rr] & & \ar[u] \im(\mathcal{H}_x) }$$](./latex/HigherGrossZagier/latex2png-HigherGrossZagier_210608687_.gif) Here the vertical arrows are all natural inclusions.
Here the vertical arrows are all natural inclusions.
By Lemma 1, 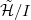 is finite dimensional, so
is finite dimensional, so 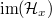 is also finite dimensional. Since
is also finite dimensional. Since 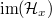 is quotient of
is quotient of 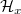 by a nonzero ideal, and
by a nonzero ideal, and 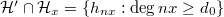 , we know the bottom row is surjective by Lemma 2. Now
, we know the bottom row is surjective by Lemma 2. Now 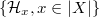 generate
generate 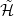 as an algebra, so the top row is also surjective. By Lemma 1,
as an algebra, so the top row is also surjective. By Lemma 1, 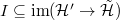 , so the map
, so the map 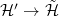 is surjective as desired.
¡õ
is surjective as desired.
¡õ
References
[1]Shtukas and the Taylor expansion of $L$-functions, ArXiv e-prints (2015).
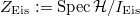 a closed subscheme of
a closed subscheme of 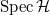 , which is reduced and 1-dimensional.
, which is reduced and 1-dimensional.
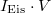 is a finite dimensional
is a finite dimensional 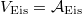 and
and 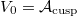 .
.
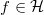 , we have the identity of rational numbers
, we have the identity of rational numbers 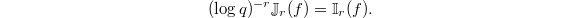
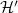 .
.
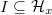 , and for any
, and for any