There are expanded notes prepared for a talk in a learning seminar on Fargues' UChicago notes Geometrization of the local Langlands correspondence, January 2016 at Columbia. Our main goal is to state the classification theorem of vector bundles on the Fargues-Fontaine curve and give a sketch of the proof. To put things in context, we first review the moduli space of vector bundles on curves and discuss the analogy between the Fargues-Fontaine curve and 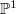 .
.
 Review: vector bundles on curves
Review: vector bundles on curves
Let 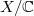 be a smooth projective curve. There is a nice moduli space parameterizing isomorphism classes of line bundles on
be a smooth projective curve. There is a nice moduli space parameterizing isomorphism classes of line bundles on 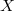 , its the Picard variety. Unlike the case of line bundles, isomorphism classes vector bundles of higher rank in general do not form nice moduli space, e.g., the jump phenomenon shows that it is not even separated. To resolve this issue, one can either remove the word "isomorphism classes'' and work directly with the moduli stack of vector bundles
, its the Picard variety. Unlike the case of line bundles, isomorphism classes vector bundles of higher rank in general do not form nice moduli space, e.g., the jump phenomenon shows that it is not even separated. To resolve this issue, one can either remove the word "isomorphism classes'' and work directly with the moduli stack of vector bundles 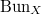 . Or more concretely, restrict one's attention to those vector bundles which are semi-stable and construct a nice moduli space of semi-stable vector bundles using Mumford's GIT. The latter coincides with the coarse moduli space of the open substack of
. Or more concretely, restrict one's attention to those vector bundles which are semi-stable and construct a nice moduli space of semi-stable vector bundles using Mumford's GIT. The latter coincides with the coarse moduli space of the open substack of 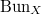 consisting of semi-stable vector bundles.
consisting of semi-stable vector bundles.
We briefly recall the notion of (semi-)stability and the Harder-Narasimhan filtration.
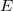 on
on 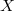 is the ratio
is the ratio 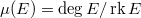 . If we draw the vector
. If we draw the vector 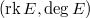 in the plane then
in the plane then 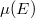 is literally its slope. Since both the degree and the rank are additive in a short exact sequence, we know the three vectors in an extension satisfy the parallel rule. In particular, if
is literally its slope. Since both the degree and the rank are additive in a short exact sequence, we know the three vectors in an extension satisfy the parallel rule. In particular, if 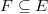 is a subbundle, then
is a subbundle, then 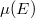 is squeezed between
is squeezed between 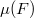 and
and 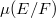 .
.
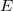 is stable (resp. semi-stable) if its slope is strictly bigger (resp. bigger) than that of any of its proper subbundle. Equivalently, by the squeeze property,
is stable (resp. semi-stable) if its slope is strictly bigger (resp. bigger) than that of any of its proper subbundle. Equivalently, by the squeeze property, 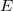 is stable (resp. semi-stable) if its slope is strictly smaller (resp. smaller) than that of any of its proper quotient bundle. By definition any line bundle is stable.
is stable (resp. semi-stable) if its slope is strictly smaller (resp. smaller) than that of any of its proper quotient bundle. By definition any line bundle is stable.
The following facts are not so difficult to prove:
- The category
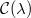 of semi-stable bundles of a fixed slope
of semi-stable bundles of a fixed slope 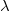 is an abelian category: in particular, kernels and cokernels are still semi-stable bundles with the same slope.
is an abelian category: in particular, kernels and cokernels are still semi-stable bundles with the same slope. - For any semi-stable bundle
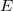 , there is a Jordan-Holder filtration
, there is a Jordan-Holder filtration 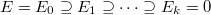 , such that each successive quotient is stable (necessarily of the same slope by the first part). In particular, the simple objects of
, such that each successive quotient is stable (necessarily of the same slope by the first part). In particular, the simple objects of 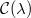 are the stable bundles.
are the stable bundles. - For any vector bundle
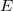 , there is a unique filtration, known as the Harder-Narasimhan filtration or the slope filtration
, there is a unique filtration, known as the Harder-Narasimhan filtration or the slope filtration 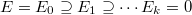 such that the successive quotients are all semi-stable with slopes strictly increasing:
such that the successive quotients are all semi-stable with slopes strictly increasing: 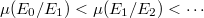 . (The construction starts off: pick the maximal subbundle
. (The construction starts off: pick the maximal subbundle 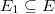 among all subbunldes of maximal slope)
among all subbunldes of maximal slope)
Let us look at the case 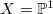 to illustrate these notions.
to illustrate these notions.
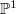 is a direct sum of line bundles. It follows that
is a direct sum of line bundles. It follows that
- The only stable bundles are line bundles. Every semi-stable bundle has integer slope
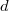 and is a direct sum of
and is a direct sum of 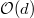 .
. - The Harder-Narasimhan filtration of any vector bundle is split.
- The map
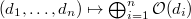 gives a bijection between integral sequences
gives a bijection between integral sequences 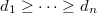 and
and 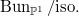
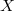 and the category of unitary representations of
and the category of unitary representations of 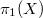 . As the simple objects, the stable vector bundles correspond exactly to the irreducible representations. For
. As the simple objects, the stable vector bundles correspond exactly to the irreducible representations. For 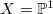 , the category of representations of
, the category of representations of 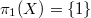 indexed by integers
indexed by integers 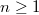 , which correspond to the trivial vector bundles
, which correspond to the trivial vector bundles 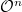 . Donaldson gives a conceptual proof of Narasimhan-Seshadri theorem by constructing a flat unitary connection on such vector bundles and the corresponding unitary representation is its monodromy representation.
. Donaldson gives a conceptual proof of Narasimhan-Seshadri theorem by constructing a flat unitary connection on such vector bundles and the corresponding unitary representation is its monodromy representation.
We will see soon that the classification of vector bundles on the Fargues-Fontaine curve remarkably resembles that of 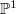 (and one may even think the Fargues-Fontaine curve as a "twisted
(and one may even think the Fargues-Fontaine curve as a "twisted 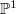 "!).
"!).
 The Fargues-Fontaine curve is like
The Fargues-Fontaine curve is like 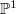 , but not quite
, but not quite
Let 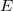 be a discretely valued non-archimedean field with uniformizer
be a discretely valued non-archimedean field with uniformizer 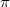 and residue field
and residue field 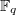 . Let
. Let 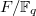 be a perfectoid field with uniformizer
be a perfectoid field with uniformizer 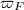 . We have constructed the Fargues-Fontaine curve (a.k.a. the fundamental curve of
. We have constructed the Fargues-Fontaine curve (a.k.a. the fundamental curve of 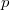 -adic Hodge theory)
-adic Hodge theory) 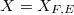 . Recall:
. Recall:
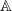 is the unique
is the unique 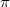 -adically complete
-adically complete 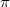 -torsion free lift of
-torsion free lift of  as an
as an 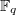 -algebra. Concretely,
-algebra. Concretely, 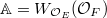 if
if 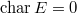 and
and ![$\mathbb{A}=\mathcal{O}_F[ [\pi] ]$](./latex/FarguesFontaine/latex2png-FarguesFontaine_91410351_-5.gif) if
if 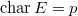 .
.![$Y=\Spa(\mathbb{A})-V(\pi[\varpi_F])$](./latex/FarguesFontaine/latex2png-FarguesFontaine_85878115_-5.gif) , where
, where ![$[\varpi_F]\in \mathbb{A}$](./latex/FarguesFontaine/latex2png-FarguesFontaine_168700019_-5.gif) is the Teichmuller lift. This is an adic space: the structure presheaf is actually a sheaf, thanks to Scholze.
is the Teichmuller lift. This is an adic space: the structure presheaf is actually a sheaf, thanks to Scholze.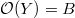 is a Frechet algebra given by the completion of
is a Frechet algebra given by the completion of ![$\mathbb{A}[1/\pi, 1/[\varpi_F]]$](./latex/FarguesFontaine/latex2png-FarguesFontaine_164648887_-5.gif) with respect to a family of norms indexed by compact intervals in
with respect to a family of norms indexed by compact intervals in 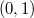 . The ring
. The ring 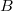 can be thought of (as least in the equal characteristic case) as holomorphic functions on the punctured open unit disk (with variable
can be thought of (as least in the equal characteristic case) as holomorphic functions on the punctured open unit disk (with variable 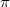 and coefficient in
and coefficient in 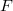 ).
).- Let
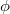 acts
acts 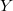 by the (lift of) Frobenius on
by the (lift of) Frobenius on 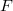 . The action is properly discontinuous and so the quotient
. The action is properly discontinuous and so the quotient 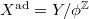 makes sense and becomes an adic space over
makes sense and becomes an adic space over 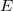 .
.
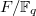 can be thought of as a test scheme over an absolute base "
can be thought of as a test scheme over an absolute base "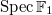 ", for the curve "
", for the curve "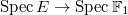 ". So
". So 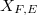 can be thought of as "
can be thought of as "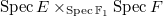 ".
".
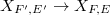 when
when 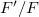 ,
, 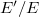 vary over finite extensions form a universal covering and hence its arithmetic etale fundamental
vary over finite extensions form a universal covering and hence its arithmetic etale fundamental 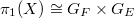 and its geometric etale fundamental group
and its geometric etale fundamental group 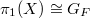 . Thus the following can be thought of as an analogue of Narasimhan-Seshadri theorem: there is an equivalence between the category of semi-stable vector bundles of slope 0 on
. Thus the following can be thought of as an analogue of Narasimhan-Seshadri theorem: there is an equivalence between the category of semi-stable vector bundles of slope 0 on 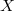 and the category of
and the category of 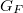 -representations over
-representations over 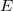 .
.
For any integer 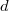 , we constructed the line bundle
, we constructed the line bundle 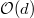 on
on 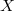 . Geometrically it is given by
. Geometrically it is given by 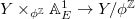 , where
, where 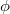 acts on
acts on 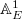 by
by 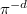 . Its global section is then given by
. Its global section is then given by 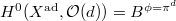 . We defined the schematic curve
. We defined the schematic curve 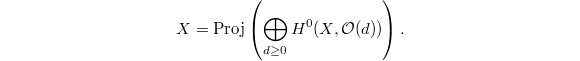 It is a scheme over
It is a scheme over 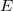 , noetherian, regular, dimensional one but not of finite type.
, noetherian, regular, dimensional one but not of finite type.
From now on assume 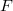 is algebraically closed. Let us see the first resemblance of
is algebraically closed. Let us see the first resemblance of 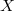 to
to 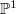 by computing the Picard group of
by computing the Picard group of 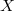 . We claim that the degree map gives an isomorphism
. We claim that the degree map gives an isomorphism 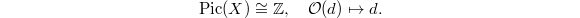 In fact, let
In fact, let 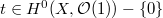 be a section whose divisor is a closed point
be a section whose divisor is a closed point 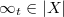 . Then
. Then ![$$X-\{\infty_t\}=\Spec B[1/t]^{\phi=\Id}.$$](./latex/FarguesFontaine/latex2png-FarguesFontaine_236105797_.gif) It turns out (requires some work) that
It turns out (requires some work) that ![$B_e:=B[1/t]^{\phi=\Id}$](./latex/FarguesFontaine/latex2png-FarguesFontaine_247481642_-5.gif) is a PID. It then follows that
is a PID. It then follows that 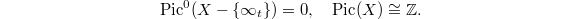
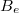 is almost Euclidean for the degree function
is almost Euclidean for the degree function  . Namely for any two nontrivial elements
. Namely for any two nontrivial elements 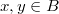 , there exists
, there exists 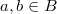 such that
such that 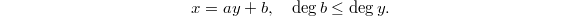 Notice Euclidean means that the strict inequality
Notice Euclidean means that the strict inequality 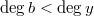 holds.
holds.
Let us see another resemblance to 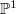 by showing the "genus" of
by showing the "genus" of 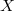 is zero, i.e.,
is zero, i.e., 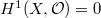 . We have an affine covering
. We have an affine covering 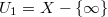 and
and 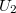 an infinitesimal neighborhood of
an infinitesimal neighborhood of 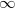 . The cohomology of coherent sheaf
. The cohomology of coherent sheaf 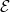 on
on 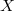 can be computed by the Cech complex
can be computed by the Cech complex 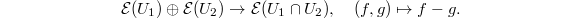 Namely
Namely 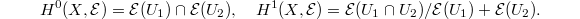 For
For 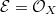 , since
, since 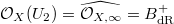 and
and ![$\mathcal{O}_X(U_1\cap U_2)=B_\mathrm{dR}:=B_\mathrm{dR}[1/t]$](./latex/FarguesFontaine/latex2png-FarguesFontaine_64022799_-5.gif) , it reads
, it reads 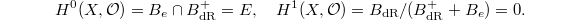 The latter has to do with the fact that
The latter has to do with the fact that 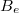 is almost Euclidean.
is almost Euclidean.
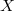 fails to satisfy Riemann-Roch:
fails to satisfy Riemann-Roch: 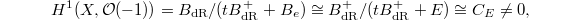 which has to do with the fact that
which has to do with the fact that 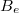 is not Euclidean. This is the main difference causing the classification of vector bundles on
is not Euclidean. This is the main difference causing the classification of vector bundles on 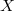 to be more complicated than the case of
to be more complicated than the case of 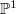 .
.
 Vector bundles on the Fargues-Fontaine curve
Vector bundles on the Fargues-Fontaine curve
Let 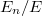 be the degree
be the degree 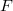 unramified extension. Notice if we replace
unramified extension. Notice if we replace 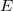 by
by 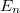 then
then 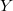 stays the same but the Frobenius changes since the residue field of
stays the same but the Frobenius changes since the residue field of 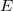 changes. Thus we have a natural degree
changes. Thus we have a natural degree 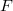 unramified cover
unramified cover 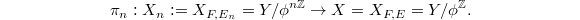
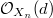 along
along 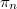 to get a vector bundle
to get a vector bundle 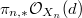 of rank
of rank 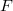 and degree
and degree 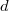 . Its slope is
. Its slope is 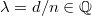 . We denote it by
. We denote it by 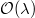 when
when 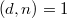 .
.
We have following easy properties analogous to the 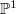 case:
case:
 .
.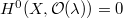 if and only
if and only 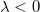 . In particular,
. In particular, 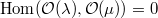 if and only
if and only 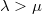 .
.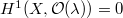 if
if 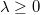 . In particular, by (a), there is no nontrivial extension of
. In particular, by (a), there is no nontrivial extension of 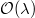 by
by 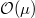 if
if 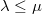 .
.
Now we can state the main classification theorem.
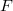 is algebraically closed.
is algebraically closed.
- The semi-stable stable vector bundles of slope
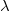 are direct sums of
are direct sums of 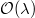 .
. - The Harder-Narasimhan filtration of any vector bundle on
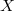 is split.
is split. - The map
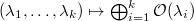 gives a bijection between sequences
gives a bijection between sequences 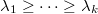 (
(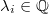 ) and
) and 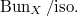
Notice (a) implies (b) by the third property in Proposition 1; (a,b) together implies (c).
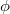 -equivariant vector bundles over
-equivariant vector bundles over 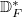 . In the mixed characteristic, this theorem is equivalent to Kedlaya's classification of
. In the mixed characteristic, this theorem is equivalent to Kedlaya's classification of 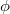 -modules over the Robba ring
-modules over the Robba ring 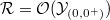 (by the expanding property of
(by the expanding property of 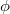 ). We are going to discuss a more geometric proof due to Fargues.
). We are going to discuss a more geometric proof due to Fargues.
 and let
and let 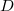 be an isocrystal over
be an isocrystal over 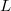 . Then the vector bundle corresponding to
. Then the vector bundle corresponding to 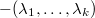 (the minus sign comes from normalization) can be realized geometrically as
(the minus sign comes from normalization) can be realized geometrically as 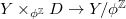 !
!
 Reduction to degree one modifications of vector bundles
Reduction to degree one modifications of vector bundles
The main goal today is to reduce to the classification theorem 2 to the following two statements about modification of vector bundles on the Fargues-Fontaine curve.
- If
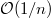 is an increasing modification of
is an increasing modification of 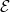 of degree one, i.e., there is an exact sequence
of degree one, i.e., there is an exact sequence 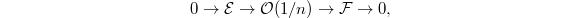 with
with 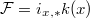 for a closed point
for a closed point  , then
, then 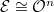 .
. - If
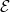 is an increasing modification of
is an increasing modification of 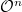 of degree one,
of degree one, 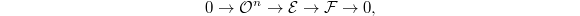 then
then 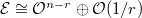 for some
for some 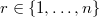 .
.
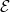 at
at 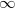 are given by specifying a lattice in
are given by specifying a lattice in 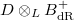 , where
, where 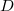 is the isocrystal with the same slopes as
is the isocrystal with the same slopes as 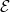 . Moreover, the degree one modification are given by the lattices satisfying the minuscule condition. Then Theorem 3 are proved by showing that all lattices corresponding to the desired modification can be realized as the period lattices of
. Moreover, the degree one modification are given by the lattices satisfying the minuscule condition. Then Theorem 3 are proved by showing that all lattices corresponding to the desired modification can be realized as the period lattices of 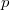 -divisible groups, which can be explicitly described. It thus boils down to the study of period maps on certain Rapoport-Zink deformation spaces of
-divisible groups, which can be explicitly described. It thus boils down to the study of period maps on certain Rapoport-Zink deformation spaces of 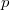 -divisible groups. Part (a) reduces to the surjectivity of the de Rham period map from the Lubin-Tate space to
-divisible groups. Part (a) reduces to the surjectivity of the de Rham period map from the Lubin-Tate space to 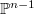 (due to Gross-Hopkins). Part (b) reduces to that any point in Drinfeld's half space
(due to Gross-Hopkins). Part (b) reduces to that any point in Drinfeld's half space 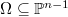 comes from the Hodge-Tate period of the dual of a Lubin-Tate formal group, which in turn reduces to that the image of the de Rham period of the Rapoport-Zink space of special formal
comes from the Hodge-Tate period of the dual of a Lubin-Tate formal group, which in turn reduces to that the image of the de Rham period of the Rapoport-Zink space of special formal 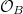 -modules of height
-modules of height 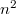 is exactly
is exactly 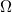 (due to Drinfeld).
(due to Drinfeld).
Our remaining goal is show that Theorem 2 is equivalent to Theorem 3, in a spirit similar to Grothendieck's proof for 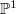 . One direction is easy to verify.
. One direction is easy to verify.
 3)
3)
- Since
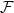 has degree 1 and rank 0, we know that
has degree 1 and rank 0, we know that 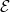 has degree 0 and rank
has degree 0 and rank 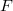 . Suppose
. Suppose 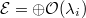 , then
, then 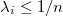 by the second property. Since
by the second property. Since 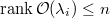 , we know that
, we know that 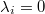 or
or 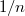 . But
. But 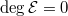 , so
, so 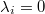 .
. - Similarly, we have
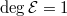 and
and 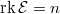 . Suppose
. Suppose 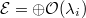 , then
, then 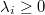 by the second property. Therefore one
by the second property. Therefore one 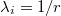 and the others are all 0.
¡õ
and the others are all 0.
¡õ
The other direction is harder. We reduce to the following lemma.
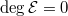 and
and 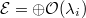 , then some
, then some 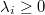 and hence
and hence 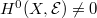 by second property.
by second property.
For the other direction, we need to show that every semi-stable vector bundle 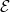 is a direct sum of
is a direct sum of 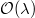 . It turns out that
. It turns out that 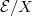 is semi-stable stable if and only if
is semi-stable stable if and only if 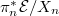 is semi-stable and
is semi-stable and 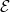 is such a direct sum of
is such a direct sum of 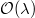 if and only if
if and only if 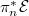 is a direct sum
is a direct sum 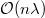 . So we may assume that
. So we may assume that 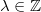 by pulling back along
by pulling back along 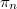 . Twisting by the line bundle
. Twisting by the line bundle  we may assume
we may assume 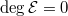 . We need to show that
. We need to show that 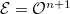 .
.
Let us only consider the case 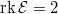 (i.e.,
(i.e., 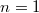 ). Let
). Let 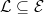 be the sub line bundle of maximal degree. It has degree
be the sub line bundle of maximal degree. It has degree 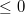 since
since 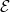 is semi-stable of degree 0. Write
is semi-stable of degree 0. Write 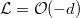 . We know that
. We know that 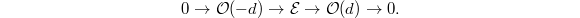 If
If  , then
, then 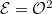 by the third property. If
by the third property. If 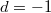 , then by assumption that
, then by assumption that 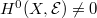 , hence there is an injection
, hence there is an injection 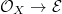 , which contradicts the maximality of
, which contradicts the maximality of 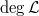 . More generally, if
. More generally, if 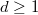 , then
, then 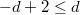 . There is an injection
. There is an injection 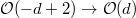 . Pullback the exact sequence we obtain a new exact sequence
. Pullback the exact sequence we obtain a new exact sequence 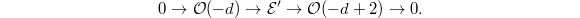 Hence by assumption
Hence by assumption 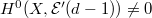 , which gives an injection
, which gives an injection 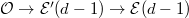 , i.e.
, i.e. 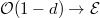 , which contradicts the maximality of
, which contradicts the maximality of 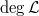 .
¡õ
.
¡õ
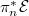 in order to use the hypothesis when
in order to use the hypothesis when 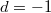 .
.
Now it remains to prove that Theorem 3 implies the statement in Lemma 1.
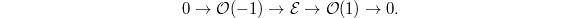 We need to show that
We need to show that 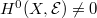 . Choose an injection
. Choose an injection 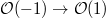 . Then pushing out gives
. Then pushing out gives 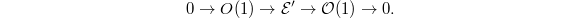 Hence
Hence 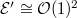 by the third property and we have
by the third property and we have 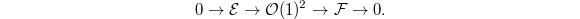 Here
Here 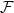 is degree 2 torsion sheaf (cokernel of
is degree 2 torsion sheaf (cokernel of  ). Choose a degree 1 subsheaf
). Choose a degree 1 subsheaf  and pullback we obtain a degree one modification
and pullback we obtain a degree one modification 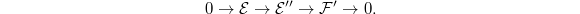 Hence
Hence 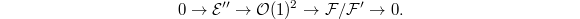 Taking dual
Taking dual  and twist by
and twist by 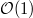 we obtain another degree one modification
we obtain another degree one modification 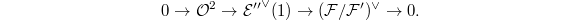 By Theorem 3 (b) we know that either
By Theorem 3 (b) we know that either 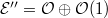 or
or 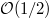 . In either case:
. In either case:
- We have
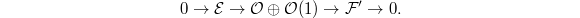 Notice
Notice 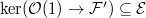 is either
is either 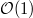 or
or 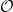 , so
, so 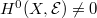 .
. - We have
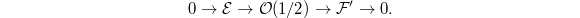 By Theorem 3 (1) we know that
By Theorem 3 (1) we know that 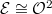 , hence
, hence 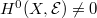 .
¡õ
.
¡õ
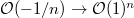 to get a degree
to get a degree 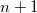 modification
modification 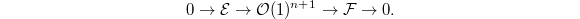 Then one write this as a sequence of degree one modifications and use Theorem 3 (a) or (b) at each step.
Then one write this as a sequence of degree one modifications and use Theorem 3 (a) or (b) at each step.
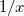 has divisor
has divisor 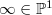 and
and ![$\mathbb{P}^1-\{\infty\}=\Spec k[x]$](./latex/FarguesFontaine/latex2png-FarguesFontaine_164275513_-5.gif) is a PID and hence
is a PID and hence 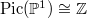 .
.
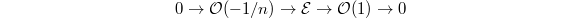 is exact, then
is exact, then