These are expanded notes prepared for a talk in a learning seminar on Caraiani-Scholze's paper On the generic part of the cohomology of compact unitary Shimura varieties, Spring 2016 at Columbia. We summarize the major ingredients of the proof, explain the preservation of perversity under the Hodge-Tate period map and deduce the main theorems: 1) the existence of Galois representations associated to the torsion classes in betti cohomology of certain compact unitary Shimura varieties; 2) after localized at a maximal ideal of the Hecke algebra satisfying a genericity assumption, the 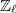 -cohomology is concentrated in the middle degree and torsion-free.
-cohomology is concentrated in the middle degree and torsion-free.
 Torsion Galois representations
Torsion Galois representations
Recall our set-up. Let 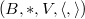 be a PEL datum of type A:
be a PEL datum of type A:
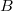 is a finite dimensional simple
is a finite dimensional simple  -algebra with center a CM field
-algebra with center a CM field 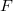 .
. is positive involution of second kind on
is positive involution of second kind on 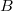 (so
(so 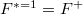 is totally real).
is totally real).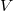 is a
is a 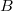 -module.
-module.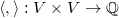 is an alternating form that is
is an alternating form that is  -Hermitian, i.e.,
-Hermitian, i.e., 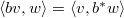 .
.
The PEL datum models the first cohomology of a polarized abelian variety of dimension 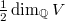 with endomorphism by
with endomorphism by 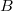 . Let
. Let 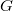 be the group of the automorphisms of
be the group of the automorphisms of 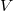 (as a
(as a 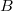 -module) that preserves
-module) that preserves 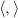 up to a similitude factor. Let
up to a similitude factor. Let 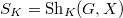 be the associated unitary Shimura variety, which is a moduli space of such abelian varieties with
be the associated unitary Shimura variety, which is a moduli space of such abelian varieties with 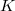 -level structure.
-level structure.
Assume we are in one of the following two extremal cases:
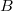 is a division algebra and
is a division algebra and 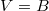 as a
as a 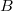 -module. In this case
-module. In this case 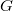 is an anisotropic unitary group (in
is an anisotropic unitary group (in 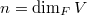 variables) and has no endoscopy.
variables) and has no endoscopy. 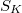 is an example of Kottwitz's simple Shimura varieties (including those considered by Harris-Taylor).
is an example of Kottwitz's simple Shimura varieties (including those considered by Harris-Taylor).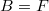 ,
, 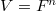 (equivalently
(equivalently 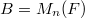 ,
, 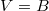 ). Assume
). Assume 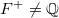 to ensure
to ensure 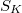 is compact. Assume that
is compact. Assume that 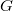 is quasi-split at all finite places. In this case
is quasi-split at all finite places. In this case 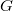 has most endoscopy and causes most difficulty in the stable trace formula. Wei may like this case more (
has most endoscopy and causes most difficulty in the stable trace formula. Wei may like this case more (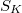 appears in his arithmetic fundamental lemma).
appears in his arithmetic fundamental lemma).
Assume 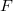 ,
, 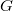 ,
, 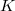 are unramified outside a finite set of primes
are unramified outside a finite set of primes 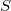 (and
(and 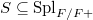 in the second case). Let
in the second case). Let ![$\mathbb{T}^S=\mathbb{Z}[G(\mathbb{A}_f^S)\sslash K^S]$](./latex/CaraianiScholze/latex2png-CaraianiScholze_96960391_-7.gif) be the unramified Hecke algebra. Let
be the unramified Hecke algebra. Let 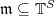 be a maximal ideal. The first main result constructs an associated torsion Galois representation.
be a maximal ideal. The first main result constructs an associated torsion Galois representation.
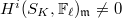 for some
for some 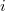 . Thee there is a semisimple Galois representation
. Thee there is a semisimple Galois representation 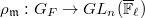 unramified outside
unramified outside 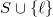 associated to
associated to 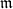 .
.
The proof requires three major ingredients:
(1) Sug Woo Shin has constructed Galois representations attached to the system of (characteristic 0) Hecke eigenvalues appearing in the cohomology of the Shimura varieties and Igusa varieties (in the above two extremal cases), by stable trace formula. In particular, there exists a Galois representation associated to system of Hecke eigenvalues in ![$[H_c(\Ig^b, \overline{\mathbb{Q}_\ell})]$](./latex/CaraianiScholze/latex2png-CaraianiScholze_109357014_-5.gif) .
.
(2) The construction of the (Hecke equivalent) Hodge-Tate period map from the infinite level Shimura variety to the flag variety 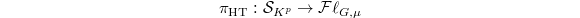 (for any Shimura varieties of Hodge type), whose fibers are related to the Igusa varieties (for any Shimura varieties of PEL type). In particular,the main result of Chap. 4 shows that for any geometric point
(for any Shimura varieties of Hodge type), whose fibers are related to the Igusa varieties (for any Shimura varieties of PEL type). In particular,the main result of Chap. 4 shows that for any geometric point 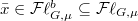 , the fiber above
, the fiber above 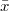 ,
, 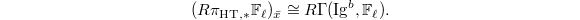
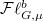 of the adic space
of the adic space 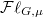 form a stratification and becomes the Newton stratification on the Shimura variety via pullback along
form a stratification and becomes the Newton stratification on the Shimura variety via pullback along 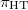 . To define
. To define 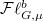 , one identifies
, one identifies 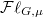 with the
with the 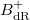 -affine Grassmannian
-affine Grassmannian 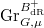 (using
(using 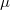 is minuscule) and notices that a
is minuscule) and notices that a 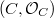 -point of
-point of 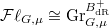 gives a
gives a 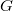 -bundle on the Fargues-Fontaine curve by modifying the trivial bundle along
-bundle on the Fargues-Fontaine curve by modifying the trivial bundle along 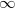 , hence corresponds to an element
, hence corresponds to an element 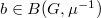 by classification of
by classification of 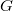 -bundles on the Fargues-Fontaine curve. Since a Newton stratum of the Shimura variety is a product of the corresponding Igusa variety and the Rapoport-Zink space, passing to the infinite level
-bundles on the Fargues-Fontaine curve. Since a Newton stratum of the Shimura variety is a product of the corresponding Igusa variety and the Rapoport-Zink space, passing to the infinite level 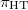 then can be realized as its local analogue for the infinite level Rapoport-Zink space (after Scholze-Weinstein), hence the fiber becomes the Igusa variety.
then can be realized as its local analogue for the infinite level Rapoport-Zink space (after Scholze-Weinstein), hence the fiber becomes the Igusa variety.
(3) The perversity of 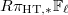 (for any compact Shimura variety of PEL type), which has the following consequence:
(for any compact Shimura variety of PEL type), which has the following consequence:
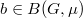 is minimal (i.e., d=
is minimal (i.e., d=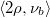 is minimal, i.e.,
is minimal, i.e., 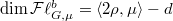 is maximal) such that
is maximal) such that 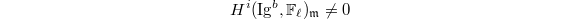 for some
for some 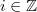 . Then
. Then 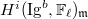 is concentrated in degree
is concentrated in degree 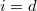 .
.
Using these 3 ingredients, now we can finish the proof of Theorem 1.
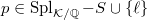 be any prime. We have a Hochschild-Serre spectral sequence
be any prime. We have a Hochschild-Serre spectral sequence 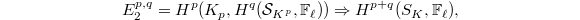 which computes the cohomology of the classical Shimura variety
which computes the cohomology of the classical Shimura variety 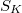 using the cohomology of the perfectoid Shimura variety
using the cohomology of the perfectoid Shimura variety 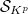 . It follows that
. It follows that 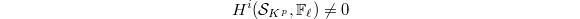 for some
for some 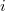 . On the other hand, the Leray spectral sequence for the Hodge-Tate period map
. On the other hand, the Leray spectral sequence for the Hodge-Tate period map 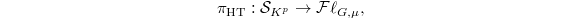 gives
gives 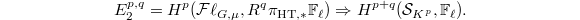 Therefore
Therefore 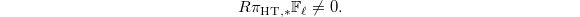 Since everything is compatible with the Hecke action away from
Since everything is compatible with the Hecke action away from  , using the Ingredient (2) we know that there exists some
, using the Ingredient (2) we know that there exists some  , such that
, such that 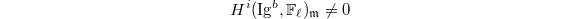 for some
for some 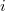 . Pick minimal such
. Pick minimal such 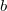 , by the perversity (Ingredient (3)), we know that
, by the perversity (Ingredient (3)), we know that 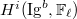 is concentrated in one degree. Therefore
is concentrated in one degree. Therefore 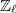 -coefficient cohomology is also concentrated in one degree and torsion-free. By Poincare duality (applied to the dual system of Hecke eigenvalues), this is also true for
-coefficient cohomology is also concentrated in one degree and torsion-free. By Poincare duality (applied to the dual system of Hecke eigenvalues), this is also true for 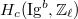 . Hence
. Hence 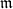 shows up in
shows up in ![$[H_c(\Ig^b, \overline{\mathbb{Q}_\ell})]$](./latex/CaraianiScholze/latex2png-CaraianiScholze_109357014_-5.gif) , where the Galois representation lifting
, where the Galois representation lifting 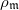 exists by Ingredient (1).
¡õ
exists by Ingredient (1).
¡õ
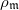 is not found in
is not found in 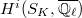 , but rather goes through the cohomology of the perfectoid Shimura variety and Igusa tower, which secretly constructs congruences between automorphic forms of different weights and levels at
, but rather goes through the cohomology of the perfectoid Shimura variety and Igusa tower, which secretly constructs congruences between automorphic forms of different weights and levels at 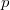 .
.
 Vanishing of torsion
Vanishing of torsion
Now let us come to the second main result, which asserts the "generic part" of the cohomology of our compact unitary Shimura varieties vanishes outside the middle degree.
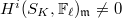 for some
for some 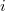 . Assume there is a prime
. Assume there is a prime 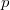 which splits completely in
which splits completely in 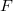 and
and 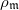 is unramified and decomposed generic at all places of
is unramified and decomposed generic at all places of 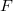 above
above 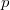 . Then
. Then 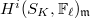 is concentrated in the middle degree
is concentrated in the middle degree 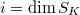 . In particular,
. In particular, 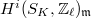 is concentrated in the middle degree and torsion-free.
is concentrated in the middle degree and torsion-free.
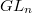 ) are useful for proving modularity lifting results for
) are useful for proving modularity lifting results for 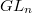 over general number fields (after Calegari-Geraghty), where numerical coincidence in the usual Taylor-Wiles method fails.
over general number fields (after Calegari-Geraghty), where numerical coincidence in the usual Taylor-Wiles method fails.
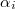 are distinct and for any
are distinct and for any 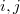
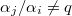 . Any characteristic 0 lift is then a direct sum of characters
. Any characteristic 0 lift is then a direct sum of characters 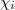 such
such 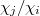 is not a cyclotomic character (since there is no nontrivial extension between
is not a cyclotomic character (since there is no nontrivial extension between 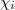 's by the Euler characteristic formula). Such a local Galois representation corresponds to a generic principal series representation of
's by the Euler characteristic formula). Such a local Galois representation corresponds to a generic principal series representation of 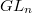 under local Langlands (hence its name).
under local Langlands (hence its name).
Generic principal series are mapped to zero under the Jacquet-Langlands correspondence to any group that is not quasi-split. As we saw last time, using this one deduces that 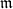 only contributes to the "most ordinary part" of the Igusa variety:
only contributes to the "most ordinary part" of the Igusa variety:
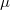 depends on the signature of
depends on the signature of 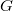 , the assumption in Theorem 3 can be relaxed according the the signature of
, the assumption in Theorem 3 can be relaxed according the the signature of 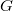 in order to ensure that
in order to ensure that 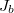 is not quasi-split unless
is not quasi-split unless 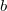 is
is 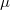 -ordinary. For example, when the signature is
-ordinary. For example, when the signature is 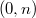 for all but one infinite place, one needs to require that
for all but one infinite place, one needs to require that 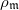 is unramified and decomposed generic at only one place of
is unramified and decomposed generic at only one place of 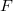 . In any case, when
. In any case, when 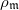 has sufficiently large image, the assumption is always satisfied by Chebotarev's density.
has sufficiently large image, the assumption is always satisfied by Chebotarev's density.
Theorem 3 now follows easily from the genericity and the three main ingredients.
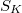 is compact, by Poincare duality, it suffices to show that
is compact, by Poincare duality, it suffices to show that 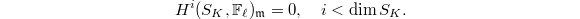 By the same argument as in proof of Theorem 1, it suffices to show that for any
By the same argument as in proof of Theorem 1, it suffices to show that for any 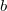 ,
, 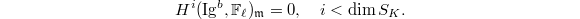 Again take any minimal
Again take any minimal 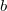 as in the proof of Theorem 1. By genericity, we know
as in the proof of Theorem 1. By genericity, we know 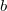 must be
must be 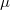 -ordinary, hence
-ordinary, hence 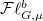 is
is 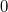 -dimensional (notice the order-reversing!) and
-dimensional (notice the order-reversing!) and 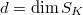 . By perversity,
. By perversity, 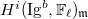 vanishes for
vanishes for 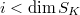 .
¡õ
.
¡õ
 The Hodge-Tate period map preserves perversity
The Hodge-Tate period map preserves perversity
Finally, let us explain the proof of the perversity result. Let 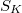 be any compact Shimura variety of PEL type with hyperspecial level at
be any compact Shimura variety of PEL type with hyperspecial level at 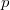 .
.
To motivate, recall two useful results for perverse sheaves in algebraic geometry:
- Any simple perverse sheaf
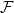 on a scheme
on a scheme 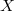 of finite type is of the form
of finite type is of the form ![$j_{!*}(\mathcal{L}[\dim Y])$](./latex/CaraianiScholze/latex2png-CaraianiScholze_237899069_-5.gif) for some locally closed subscheme
for some locally closed subscheme 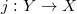 and a local system
and a local system 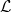 on
on 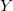 . In particular,
. In particular, 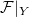 is concentrated in one degree.
is concentrated in one degree. - Any finite (more generally, any small) map
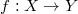 preserves perversity: if
preserves perversity: if 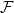 is a perverse sheaf on
is a perverse sheaf on 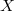 , then
, then 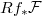 is a perverse sheaf on
is a perverse sheaf on 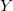 .
.
By the minimality, we know that 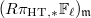 has support on the union
has support on the union  So it has support in a closed subset of dimension equal to
So it has support in a closed subset of dimension equal to 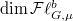 . The result then would follow if
. The result then would follow if 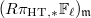 is "perverse". Why should it be? The intuition is that
is "perverse". Why should it be? The intuition is that 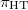 is an affine and partially proper (i.e., satisfies valuative criterion in the category of adic spaces). If we were working with schemes, this would mean
is an affine and partially proper (i.e., satisfies valuative criterion in the category of adic spaces). If we were working with schemes, this would mean 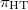 is affine and proper, hence finite, and finite morphisms preserve perversity. Of course all the beauty of
is affine and proper, hence finite, and finite morphisms preserve perversity. Of course all the beauty of 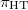 lies in its very non finite-type behavior, so we cannot literally say this. On the other hand, because of Ingredient (2), we only need to show the sheaf is perverse when restricted on an affinoid etale neighborhood
lies in its very non finite-type behavior, so we cannot literally say this. On the other hand, because of Ingredient (2), we only need to show the sheaf is perverse when restricted on an affinoid etale neighborhood 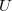 of
of  . Then we can pass to the special fiber (by the perfectoidness), where
. Then we can pass to the special fiber (by the perfectoidness), where 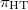 indeed becomes a finite map between affine schemes of finite type over the residual field.
indeed becomes a finite map between affine schemes of finite type over the residual field.
The other issue is that 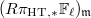 admits the action of
admits the action of 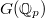 and is infinite dimensional. So it can only be perverse (or just constructible) after taking
and is infinite dimensional. So it can only be perverse (or just constructible) after taking 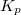 -invariants for
-invariants for 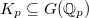 open compact. So the idea for proving the perversity Theorem 2 is then to pass to finite levels and special fibers. Let us be more precise.
open compact. So the idea for proving the perversity Theorem 2 is then to pass to finite levels and special fibers. Let us be more precise.
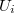 of affinoid etale neighborhoods
of affinoid etale neighborhoods 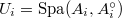 of
of 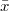 such that its pullback under
such that its pullback under 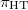 (denoted by
(denoted by 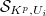 ) is affinoid perfectoid. For each such
) is affinoid perfectoid. For each such 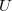 , we have a formal model
, we have a formal model 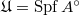 and correspondingly a formal model
and correspondingly a formal model 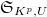 for
for 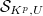 . For any such
. For any such 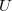 , for
, for 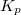 a sufficiently small pro-
a sufficiently small pro-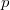 open compact subgroup of
open compact subgroup of 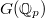 , we have a continuous action of
, we have a continuous action of 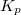 on
on 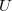 , which induces the trivial on the special fiber
, which induces the trivial on the special fiber 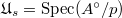 .
.
We choose such 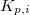 sufficiently small for each
sufficiently small for each 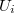 so that
so that 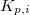 's shrink to 1. Then we know that the fiber at
's shrink to 1. Then we know that the fiber at 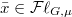 can be computed using the cohomology of the special fiber using the right upper corner of the following diagram,
can be computed using the cohomology of the special fiber using the right upper corner of the following diagram, ![$$\xymatrix{ S_{K^p, U}/K_p \ar[r]^-{\pi_\mathrm{HT}} \ar[d]^{\lambda} & U/K_p \ar[d]^{\lambda} \\ \mathfrak{S}_{K_pK^p,U,s} \ar[r]^-{\pi_\mathrm{HT}} & \mathfrak{U}_s.}$$](./latex/CaraianiScholze/latex2png-CaraianiScholze_185541466_.gif) When shrinking
When shrinking 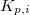 , we obtain
, we obtain 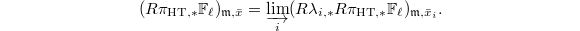 Here
Here 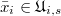 is the specialization of
is the specialization of 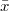 . Now we can compute using the left lower corner as well, namely, first specialize, then apply
. Now we can compute using the left lower corner as well, namely, first specialize, then apply 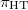 (which now becomes a finite map between schemes of finite type). Because the general fact that specialization (aka, nearby cycle) preserves perversity, we know that each individual term in the direct limit is concentrated in degree
(which now becomes a finite map between schemes of finite type). Because the general fact that specialization (aka, nearby cycle) preserves perversity, we know that each individual term in the direct limit is concentrated in degree 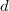 . Hence the direct limit itself is also concentrated in degree
. Hence the direct limit itself is also concentrated in degree 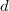 .
¡õ
.
¡õ
![$[H_c(\Ig^b, \overline{\mathbb{Q}_\ell})]_\mathfrak{m}=0$](./latex/CaraianiScholze/latex2png-CaraianiScholze_206710306_-5.gif) .
.