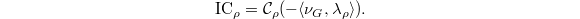These are notes for two talks in the Beyond Endoscopy Learning Seminar at Columbia, Spring 2018. Our main references are [1] and [2].
Recall that two key constructions are required in the Braverman-Kazhdan program for proving analytic continuation and functional equations for general Langlands  -function
-function 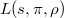 . One is a suitable space of Schwartz functions
. One is a suitable space of Schwartz functions 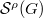 at each local place, containing a distinguished function encoding the unramified local
at each local place, containing a distinguished function encoding the unramified local 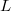 -factor (known as the basic function
-factor (known as the basic function 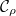 after Sakellaridis). The other is a generalized Fourier transform (known as the Hankel transform after Ngo) preserving the Schwartz space and the basic function. With a global Poisson summation formula, one should be able to establish the desired analytic properties of
after Sakellaridis). The other is a generalized Fourier transform (known as the Hankel transform after Ngo) preserving the Schwartz space and the basic function. With a global Poisson summation formula, one should be able to establish the desired analytic properties of 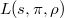 in a way analogous to Godement-Jacquet theory for standard
in a way analogous to Godement-Jacquet theory for standard 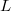 -function on
-function on 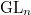 . Our goal today is to discuss the basic function
. Our goal today is to discuss the basic function 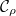 and to explain its an algebro-geometric interpretation due to Bouthier-Ngo-Sakellaridis, using the
and to explain its an algebro-geometric interpretation due to Bouthier-Ngo-Sakellaridis, using the 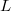 -monoid
-monoid 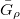 appeared in previous talks and its arc space.
appeared in previous talks and its arc space.
 Satake/Langlands parameters
Satake/Langlands parameters
Let 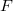 be a non-archimedean local field. Let
be a non-archimedean local field. Let 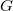 be a split reductive group over
be a split reductive group over 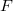 . Let
. Let 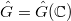 be its dual group. Let
be its dual group. Let 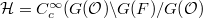 be the spherical Hecke algebra. Recall that the classical Satake transform
be the spherical Hecke algebra. Recall that the classical Satake transform ![$$\mathrm{Sat}:\mathcal{H}\rightarrow \mathbb{C}[X _ * (T)],\quad f\mapsto \left( t\mapsto\delta_B(t)^{1/2}\int_{N(F)}f(tn)dn\right),$$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_57663283_.gif) induces an algebra isomorphism onto the
induces an algebra isomorphism onto the  -invariants
-invariants ![$$\mathcal{H}\xrightarrow{\sim} \mathbb{C}[X _ * (T)]^W.$$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_77559797_.gif) An unramified representation
An unramified representation  of
of  corresponds to a 1-dimensional character of
corresponds to a 1-dimensional character of 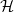 , given by its action on the spherical vector
, given by its action on the spherical vector 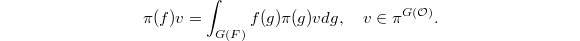 Langlands noticed that
Langlands noticed that ![$\mathbb{C}[X _ * (T)]^W$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_47296473_-5.gif) is the coordinate ring of the variety
is the coordinate ring of the variety 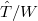 , so a 1-dimensional character
, so a 1-dimensional character ![$\mathbb{C}[X _ * (T)]^W$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_47296473_-5.gif) corresponds to a point
corresponds to a point 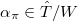 , i.e., a semisimple conjugacy class in
, i.e., a semisimple conjugacy class in 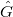 . In this we obtain a bijection
. In this we obtain a bijection 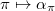 between unramified representations of
between unramified representations of 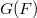 and the Satake (or rather, Langlands) parameters. The Satake transform is then characterized by the identity
and the Satake (or rather, Langlands) parameters. The Satake transform is then characterized by the identity 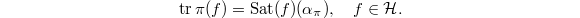 Also notice that the target of the Satake isomorphism can be identified with the representation ring of
Also notice that the target of the Satake isomorphism can be identified with the representation ring of 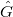 , and thus with the
, and thus with the 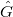 -invariant regular functions
-invariant regular functions 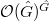 on
on 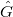 (via the trace map).
(via the trace map).
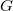 and the size of the residue field
and the size of the residue field 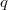 . In fact, the Satake isomorphism can be defined over
. In fact, the Satake isomorphism can be defined over ![$\mathbb{Z}[q^{\pm1/2}]$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_119972762_-5.gif) .
.
 Basic functions
Basic functions
The importance of the Satake parameter is due to its key role in defining the unramified local 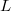 -factor
-factor 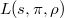 . Let
. Let 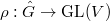 be an irreducible representation. Recall by definition
be an irreducible representation. Recall by definition 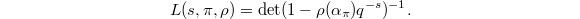 Now if we have a diagonal matrix
Now if we have a diagonal matrix 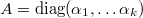 , then
, then 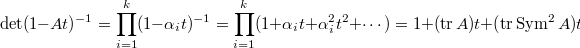 Therefore
Therefore 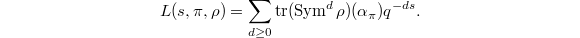 To remove the dependence on
To remove the dependence on 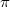 , we are motivated to introduce the following definition.
, we are motivated to introduce the following definition.
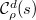 to be the inverse under the Satake transform of the function
to be the inverse under the Satake transform of the function 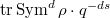 (so
(so 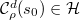 for any given
for any given 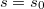 . Define the basic function to be
. Define the basic function to be 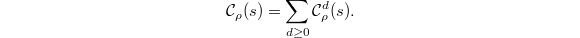 When
When 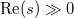 , the sum is locally finite and makes sense as a function on
, the sum is locally finite and makes sense as a function on 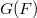 .
.
Even though each 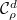 is compactly supported (with support lies in the
is compactly supported (with support lies in the 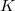 -double cosets indexed by dominant coweights of
-double cosets indexed by dominant coweights of 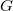 corresponding to weights of
corresponding to weights of 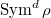 ), the support gets larger when
), the support gets larger when 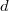 increases and
increases and 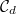 is not longer compactly supported. Moreover, the values of
is not longer compactly supported. Moreover, the values of 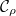 on each
on each 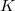 -double cosets can be written down in terms of representation theory (related to Kazhdan-Lusztig polynomials) and thus involve quite complicated combinatorial quantities.
-double cosets can be written down in terms of representation theory (related to Kazhdan-Lusztig polynomials) and thus involve quite complicated combinatorial quantities.
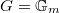 , and
, and 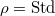 . Since
. Since 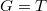 , both the source and target of the Satake isomorphism are identified as functions on
, both the source and target of the Satake isomorphism are identified as functions on 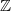 . The Satake transform sends the characteristic function
. The Satake transform sends the characteristic function 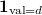 to
to 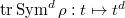 . So
. So 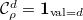 and the basic function is given by
and the basic function is given by 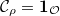 (always viewed as a function on
(always viewed as a function on 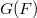 ). This generalizes to the standard representation of
). This generalizes to the standard representation of 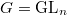 , in which case
, in which case 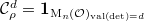 (this is already a nontrivial computation) and hence
(this is already a nontrivial computation) and hence 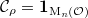 .
.
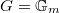 , and
, and 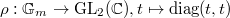 (i.e.,
(i.e., 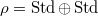 ). Then
). Then 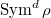 has dimension
has dimension 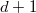 given by
given by 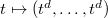 , whose trace is
, whose trace is 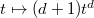 . So the corresponding basic function is given by
. So the corresponding basic function is given by 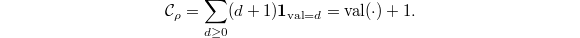 This is no longer the characteristic function of any set. More generally, take
This is no longer the characteristic function of any set. More generally, take  and
and 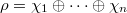 (
( ). Then
). Then 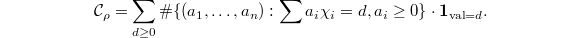 So the value of
So the value of 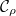 encodes partition numbers, and can not have simple formula. We also see that the support of
encodes partition numbers, and can not have simple formula. We also see that the support of 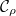 is contained in the cone generated by the weights of
is contained in the cone generated by the weights of 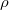 .
.
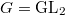 and
and 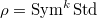 . Then computing
. Then computing 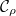 amounts to decomposing
amounts to decomposing 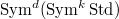 into irreducibles, again this is a difficult combinatoric problem. In fact, we have
into irreducibles, again this is a difficult combinatoric problem. In fact, we have ![$$\Sym^d\Sym^k\cong \bigoplus_{i=0}^{[d k/2]}(\Sym^{dk- 2i} \otimes \det{}^{dk-i})^{\oplus N(d,k,i)}.$$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_41067022_.gif) Here the multiplicity
Here the multiplicity 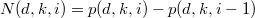 , and
, and 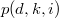 is the number of partitions of
is the number of partitions of 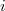 into at most
into at most 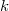 parts, having largest part at most
parts, having largest part at most 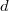 .
.
I hope these examples illustrate that writing down an explicit formula for the basic function is quite hopeless in general (but see Wen-Wei Li's paper). Instead we would like to focus on finding some natural algebro-geometric object which encodes these combinatoric information. This is the main motivation to introduce the 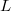 -monoid.
-monoid.
 Vinberg's universal monoids
Vinberg's universal monoids
Let 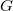 be a split reductive group over a field
be a split reductive group over a field 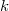 (later
(later 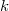 will be the residue field of the local field
will be the residue field of the local field 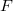 ). Assume
). Assume 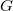 has a nontrivial map to
has a nontrivial map to 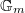 , denoted by
, denoted by 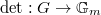 . Assume
. Assume 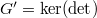 is semisimple and simply-connected. Our first goal is to construct Vinberg's universal monoid
is semisimple and simply-connected. Our first goal is to construct Vinberg's universal monoid 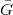 . It is a normal affine variety
. It is a normal affine variety 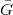 fitting into a commutative diagram
fitting into a commutative diagram ![$$\xymatrix{ G^+ \ar@{^(->}[r] \ar[d] & \bar G \ar[d]\\ \mathbb{G}_m^r \ar@{^(->}[r] & \mathbb{A}^r.}$$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_157770561_.gif) This monoid is universal in the sense that every reductive monoid with derived group equal to
This monoid is universal in the sense that every reductive monoid with derived group equal to 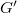 can be obtained by base change from
can be obtained by base change from 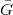 (in fact the construction of
(in fact the construction of 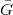 will only depend on
will only depend on 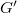 ).
).
Let 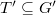 be a maximal torus of
be a maximal torus of 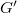 . Let
. Let 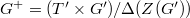 . Let
. Let  be the semisimple rank of
be the semisimple rank of 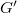 . Let
. Let 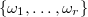 be the set of fundamental weights of
be the set of fundamental weights of 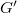 (dual to the coroots). Let
(dual to the coroots). Let 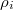 be the fundamental representation of
be the fundamental representation of 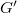 associated to
associated to 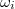 . We extend
. We extend 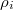 from
from 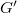 to
to 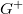 by
by 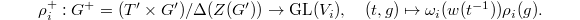 Here
Here 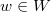 is the longest element in the Weyl group. We also extend the simple roots
is the longest element in the Weyl group. We also extend the simple roots 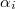 from
from 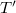 to
to 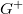 by
by 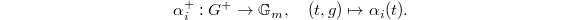 These extensions together give a homomorphism
These extensions together give a homomorphism 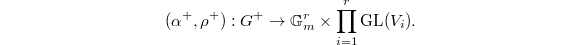
 . Then
. Then 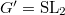 ,
, 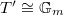 ,
, 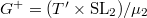 . We have
. We have 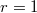 ,
, 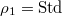 ,
, 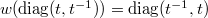 ,
, 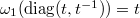 ,
, 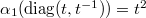 . So
. So 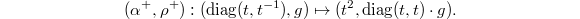 So
So 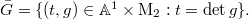 In other words, this is a monoid in
In other words, this is a monoid in 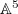 defined by the equation
defined by the equation 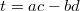 (which is smooth).
(which is smooth).
 Ngo's
Ngo's 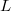 -monoids
-monoids
Now let 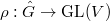 be an irreducible representation. Let
be an irreducible representation. Let 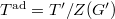 be a maximal torus in the adjoint group of
be a maximal torus in the adjoint group of 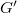 . The highest weight of
. The highest weight of 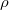 defines a cocharacter
defines a cocharacter 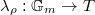 , hence a cocharacter of
, hence a cocharacter of 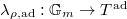 . We identify
. We identify 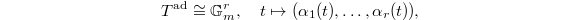 using a choice of simple roots. Then
using a choice of simple roots. Then 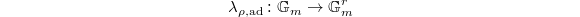 can be extended to a morphism of monoids
can be extended to a morphism of monoids 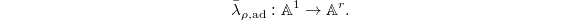
 -monoid
-monoid 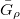 is defined by base changing the universal monoid
is defined by base changing the universal monoid 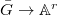 along
along 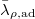 . So we have a commutative diagram
. So we have a commutative diagram ![$$\xymatrix{ \bar G_\rho^\times \ar@{^(->}[r] \ar[d] & \bar G_\rho \ar[d]\\ \mathbb{G}_m \ar@{^(->}[r] & \mathbb{A}^1.}$$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_174637471_.gif)
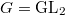 ,
, 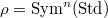 . Then
. Then 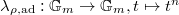 . So we have
. So we have 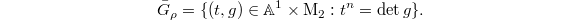 Notice that the unit group is
Notice that the unit group is  when
when  is odd and
is odd and 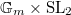 when
when 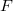 is even (the derived group is
is even (the derived group is 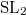 in both cases). Notice that this monoid is singular at the origin when
in both cases). Notice that this monoid is singular at the origin when 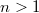 , which reflects the fact that the basic function are more complicated than the
, which reflects the fact that the basic function are more complicated than the 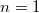 case.
case.
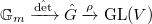 is the identity map (e.g.,
is the identity map (e.g., 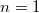 in the previous example) ensures that the unit group of
in the previous example) ensures that the unit group of 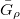 is
is 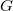 and we obtain a commutative diagram
and we obtain a commutative diagram ![$$\xymatrix{G \ar@{^(->}[r] \ar[d]^{\det } & \bar G_\rho \ar[d]\\ \mathbb{G}_m \ar@{^(->}[r] & \mathbb{A}^1.}$$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_4367534_.gif) The construction of
The construction of 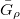 can be characterized in terms of toric varieties: it is the unique reductive monoid with unit group
can be characterized in terms of toric varieties: it is the unique reductive monoid with unit group 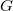 such that the closure of any maximal torus
such that the closure of any maximal torus 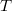 in
in 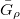 is the toric variety associated to
is the toric variety associated to 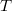 and the cone generated by the weights of
and the cone generated by the weights of 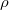 .
.
 Arc spaces
Arc spaces
Directly comes from the construction of 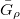 one sees that
one sees that 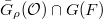 is exactly supported on the
is exactly supported on the 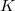 -double cosets associated dominant weights generated by the weights of
-double cosets associated dominant weights generated by the weights of 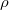 . So the basic function
. So the basic function 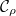 can be viewed as a function on
can be viewed as a function on 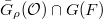 . Now take
. Now take 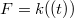 . Then we have the advantage of endowing
. Then we have the advantage of endowing 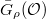 an algebro-geometric structure over the residue field
an algebro-geometric structure over the residue field 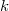 .
.
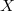 be an algebraic variety over a field
be an algebraic variety over a field 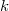 . We define its
. We define its 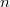 -th jet space
-th jet space 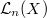 to be the functor sending a
to be the functor sending a 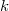 -algebra
-algebra 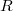 to the set
to the set ![$X(R[t]/t^{n+1})$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_142750306_-5.gif) . If
. If 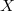 is affine, then
is affine, then 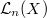 is also representable by an affine
is also representable by an affine 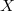 -scheme of finite type. In particular,
-scheme of finite type. In particular, ![$\mathcal{L}_n(X)(k)=X(k[t]/t^{n+1})=\Hom(k[t]/t^{n+1}, X)$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_4004438_-5.gif) consists of order-
consists of order-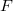 arcs in
arcs in 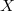 . When
. When 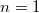 we exactly recover the tangent bundle of
we exactly recover the tangent bundle of 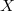 . For more general
. For more general 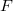 ,
, 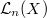 contains information about the singularities of
contains information about the singularities of 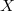 .
.
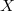 is defined by
is defined by 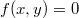 , then
, then 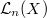 is defined by the equation
is defined by the equation 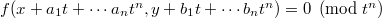 with extra variables
with extra variables 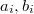 . Take
. Take 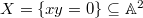 . Then
. Then 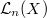 is given by
is given by 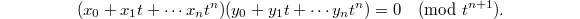 One can find
One can find 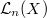 exactly has
exactly has 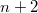 irreducible components, each isomorphic to
irreducible components, each isomorphic to 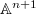 given by the first
given by the first 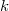 of the
of the  -coordinates are 0 and first
-coordinates are 0 and first  of the
of the 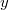 -coordinates equal to zero, where
-coordinates equal to zero, where 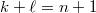 . The component with
. The component with 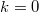 maps to the line
maps to the line 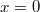 , and the component with
, and the component with 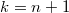 maps to the other line
maps to the other line 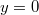 . All the rest
. All the rest 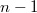 components maps to the singularity (the origin).
components maps to the singularity (the origin).
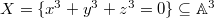 . Then
. Then 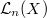 has one irreducible component of dimension
has one irreducible component of dimension 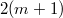 which dominates
which dominates 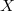 , and has one extra component of the same dimension mapping to the origin when
, and has one extra component of the same dimension mapping to the origin when 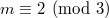 .
.
If 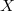 is smooth, then the natural map
is smooth, then the natural map 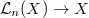 is smooth and surjective. In general, if
is smooth and surjective. In general, if 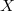 is not smooth, then
is not smooth, then 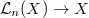 may fail to be surjective, and the transition maps can be rather complicated.
may fail to be surjective, and the transition maps can be rather complicated.
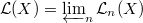 . In particular,
. In particular, ![$\mathcal{L}(X)(k)=X(k[ [t] ])=X(\mathcal{O})$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_163970499_-5.gif) , which consists of (formal) arcs
, which consists of (formal) arcs 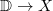 of
of 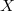 (here
(here ![$\mathbb{D}=\Spf k[ [t] ]$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_108682365_-5.gif) is the formal disc).
is the formal disc).
Again if 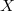 is smooth then
is smooth then 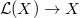 is formally smooth and surjective. A theorem of John Nash says that the inverse image of
is formally smooth and surjective. A theorem of John Nash says that the inverse image of 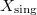 in
in 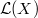 has only finitely many irreducible components, each corresponds to a component in the inverse image of
has only finitely many irreducible components, each corresponds to a component in the inverse image of 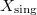 in any resolution of singularities of
in any resolution of singularities of 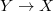 .
.
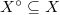 be a smooth open dense subvariety. We define
be a smooth open dense subvariety. We define 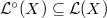 to be the space of non-degenerate arcs in
to be the space of non-degenerate arcs in 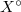 . Namely for a
. Namely for a 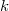 -algebra
-algebra 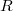 ,
, 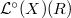 consists of arcs
consists of arcs 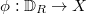 such that inverse image
such that inverse image 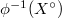 is open in
is open in 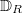 and surjects to
and surjects to 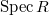 . In particular, we have
. In particular, we have 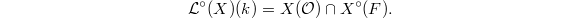
If one has a  -adic sheaf
-adic sheaf 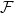 on
on 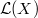 , then taking the Frobenius trace gives us a function
, then taking the Frobenius trace gives us a function 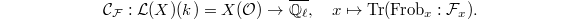 (if
(if 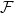 is a complex, then take alternating trace on the cohomology groups). Similarly, if we only have a sheaf on
is a complex, then take alternating trace on the cohomology groups). Similarly, if we only have a sheaf on 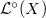 , we can still obtain a function on
, we can still obtain a function on 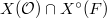 . When specializing to
. When specializing to 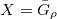 and
and 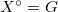 , we can obtain a function on
, we can obtain a function on 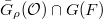 as desired. Our next goal is then to construct a canonical sheaf on
as desired. Our next goal is then to construct a canonical sheaf on 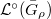 , whose associated function gives the basic function
, whose associated function gives the basic function 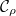 .
.
 IC sheaves and functions
IC sheaves and functions
If 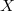 is a variety over
is a variety over 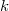 , there is a canonical sheaf associated to
, there is a canonical sheaf associated to 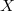 , i.e., its IC sheaf which generalizes the constant sheaf and encodes the singularities of
, i.e., its IC sheaf which generalizes the constant sheaf and encodes the singularities of 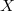 .
.
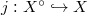 be a smooth open dense subvariety. We define
be a smooth open dense subvariety. We define 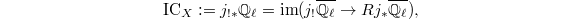 to be the middle extension of the constant sheaf on
to be the middle extension of the constant sheaf on 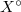 (so
(so 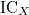 a complex of sheaves in the derived category of
a complex of sheaves in the derived category of 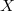 ). It is independent of the choice of
). It is independent of the choice of 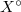 and measures the singularities of
and measures the singularities of 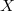 along the boundary. The shift
along the boundary. The shift ![$\mathrm{IC}_X[\dim X]$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_254964021_-5.gif) serves as the dualizing sheaf for the Poincare(-Verdier) duality for singular varieties, and is a basic example of a perverse sheaf.
serves as the dualizing sheaf for the Poincare(-Verdier) duality for singular varieties, and is a basic example of a perverse sheaf.
However, because the arc space 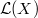 is infinite type over
is infinite type over 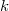 , there is no good theory of IC sheaves/perverse sheaves on
, there is no good theory of IC sheaves/perverse sheaves on 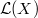 . Fortunately, the singularities of
. Fortunately, the singularities of 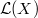 have a finite dimensional model.
have a finite dimensional model.
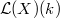 at
at 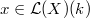 is a formal scheme
is a formal scheme 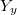 (the subscript means taking formal completion), where
(the subscript means taking formal completion), where 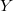 is a finite type
is a finite type 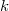 -scheme and
-scheme and 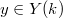 a point such that
a point such that 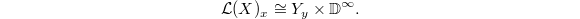
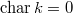 ) Finite dimensional model exists at each point
) Finite dimensional model exists at each point 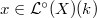 .
.
Bouthier-Ngo-Sakellaridis [1] show that the stalk 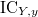 of the IC sheaf of
of the IC sheaf of 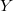 does not depend on the choice of the finite dimensional formal model
does not depend on the choice of the finite dimensional formal model 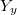 . It now makes sense to define the IC function on the non-degenerate arcs by
. It now makes sense to define the IC function on the non-degenerate arcs by 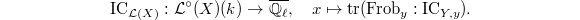 It is a numerical invariant encoding the singularities of
It is a numerical invariant encoding the singularities of 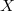 . By taking
. By taking 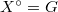 and
and 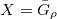 , we obtain
, we obtain 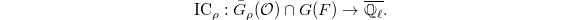
Now we can state the main theorem of [1].
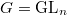 and
and 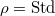 , we have
, we have 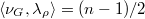 . So we recover
. So we recover  The shift
The shift 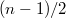 matches with the Godement-Jacquet zeta integral as well.
matches with the Godement-Jacquet zeta integral as well.
 A global model
A global model
To prove the main theorem, we need a concrete construction of the finite dimensional model of 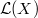 at non-degenerate arcs. To do so we make use of a global smooth projective curve
at non-degenerate arcs. To do so we make use of a global smooth projective curve 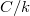 . From now on, let
. From now on, let 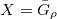 (with left and right
(with left and right 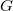 -actions).
-actions).
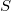 -point of the quotient stack
-point of the quotient stack ![$[X/G]$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_204507470_-5.gif) consists of a principal
consists of a principal 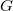 -bundle
-bundle 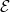 over
over 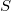 together with a
together with a 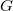 -equivariant map
-equivariant map 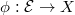 . Consider the stack
. Consider the stack ![$\Map(C, [X/G])$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_138312658_-5.gif) , whose
, whose 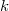 -points consists of maps
-points consists of maps ![$\phi: C\rightarrow [X/G]$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_159832340_-5.gif) , namely a principal
, namely a principal 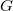 -bundle
-bundle 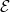 over
over 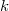 together a
together a 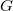 -equivariant homomorphism
-equivariant homomorphism 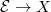 . We now add the non-degeneracy and define
. We now add the non-degeneracy and define 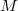 to be the open substack of
to be the open substack of ![$\Map(C, [X/G])$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_138312658_-5.gif) such that
such that 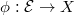 factors through
factors through 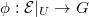 for a open subset
for a open subset 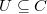 . Then one can show that
. Then one can show that 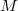 is an algebraic space locally of finite type.
is an algebraic space locally of finite type.
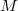 to
to 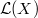 , we fix a
, we fix a 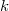 -point
-point 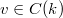 . Define
. Define 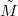 to be the stack classifying a point
to be the stack classifying a point 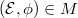 together with
together with 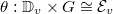 , a trivialization of
, a trivialization of 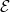 on the formal disc
on the formal disc 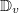 . Then we have a canonical projection
. Then we have a canonical projection 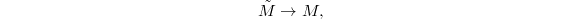 which is a torsor under
which is a torsor under 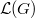 , hence is formally smooth. On the other hand, given a point
, hence is formally smooth. On the other hand, given a point 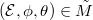 , we obtain an arc by the composite map
, we obtain an arc by the composite map 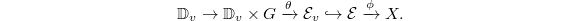 Moreover, this arc is non-degenerate (by the non-degenerate requirement when defining
Moreover, this arc is non-degenerate (by the non-degenerate requirement when defining  ). Thus we obtain a morphism
). Thus we obtain a morphism 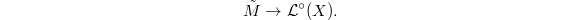
The following essentially says that there is no obstruction for deforming  -bundles while fixing the induced formal arc.
-bundles while fixing the induced formal arc.
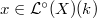 . Let
. Let 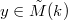 be a point such that
be a point such that 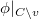 lies in the smooth locus of
lies in the smooth locus of 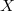 , and such that its image in
, and such that its image in 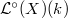 is
is  (such
(such 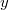 always exists by Beauville-Laszlo patching the trivial
always exists by Beauville-Laszlo patching the trivial 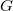 -bundle). Then
-bundle). Then 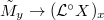 is formally smooth.
is formally smooth.
It follows that 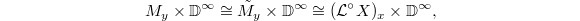 and hence
and hence 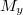 can serve as a finite dimensional formal model of
can serve as a finite dimensional formal model of 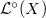 at
at  . In particular, we obtain
. In particular, we obtain 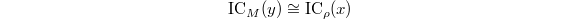
 Geometric Satake
Geometric Satake
Let 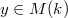 . From the fixed map
. From the fixed map 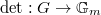 one naturally associates to
one naturally associates to 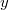 a line bundle on
a line bundle on 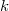 . Using the trivialization of
. Using the trivialization of 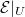 induced from
induced from 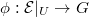 , we also obtain a generic section of this line bundle, hence a divisor
, we also obtain a generic section of this line bundle, hence a divisor 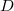 on
on 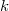 .
.
Let 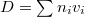 and
and 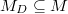 be the substack whose associated divisor is
be the substack whose associated divisor is 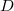 . By the Beauville-Laszlo patching, the data of a
. By the Beauville-Laszlo patching, the data of a 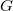 -bundle
-bundle 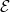 and a trivialization away from
and a trivialization away from 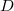 is the same as giving
is the same as giving 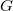 -bundles
-bundles 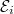 on the formal disc
on the formal disc 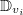 together with a trivialization on the punctured formal disc
together with a trivialization on the punctured formal disc 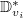 . Then we obtain a map into the affine Grassmannians
. Then we obtain a map into the affine Grassmannians 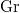 (whose
(whose 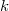 -points are
-points are 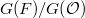 ) at
) at 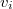 's,
's, 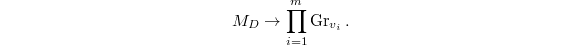 Moreover, a trivialization of
Moreover, a trivialization of 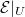 actually comes from a
actually comes from a 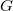 -equivariant map
-equivariant map 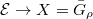 if and only if
if and only if 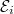 has invariant
has invariant 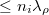 for each
for each 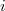 . Thus we obtain an isomorphism
. Thus we obtain an isomorphism 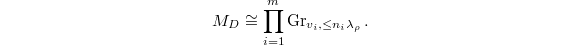 Notice each term on the right is indeed a projective variety (a Schubert variety), which models singularity of
Notice each term on the right is indeed a projective variety (a Schubert variety), which models singularity of 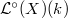 when
when 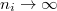 . Varying
. Varying 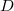 , we obtain an isomorphism
, we obtain an isomorphism 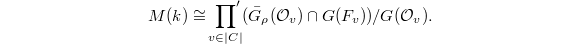 Using this isomorphism and a fixed
Using this isomorphism and a fixed  , we can choose the point
, we can choose the point  explicitly corresponding to a point
explicitly corresponding to a point 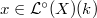 such that
such that 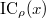 is the
is the  -component of
-component of 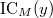 .
.
Now recall the geometric Satake correspondence.
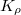 be the IC sheaf of the Schubert variety
be the IC sheaf of the Schubert variety 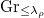 shifted by its dimension
shifted by its dimension 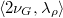 . Then the map
. Then the map 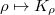 gives an equivalence of tensor categories between the finite dimensional representations of
gives an equivalence of tensor categories between the finite dimensional representations of 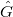 and
and 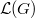 -equivariant perverse sheaves on
-equivariant perverse sheaves on 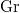 (the tensor structure given the convolution product).
(the tensor structure given the convolution product).
Bouthier-Ngo-Sakellaridis show that .$$](./latex/BouthierNgoSakellaridis/latex2png-BouthierNgoSakellaridis_57526653_.gif) (The symmetric power essentially comes from looking at the map
(The symmetric power essentially comes from looking at the map 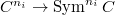 ). Hence by the geometric Satake we have
). Hence by the geometric Satake we have 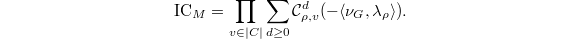 The main theorem now follows by taking the
The main theorem now follows by taking the  -component.
-component.
References
[1]On the formal arc space of a reductive monoid, Amer. J. Math. 138 (2016), no.1, 81--108.
[2]Hankel transform, Langlands functoriality and functional equation of automorphic L-functions, http://math.uchicago.edu/~ngo/takagi.pdf.
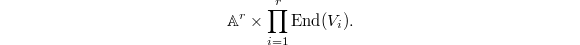
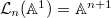 .
.
 be the half sum of all positive roots. Then
be the half sum of all positive roots. Then