(see Figure 1.1 for a proof). A triple of integers
(a,b,c) satisfying
is called a Pythagorean
triple. Here are a few examples of Pythagorean triples.
Number theory is the study of the divisibility properties of the integers. The natural numbers are one of the oldest and the most fundamental mathematical objects. Since ancient time, human beings have been fascinated by the magical, mystical properties of numbers. The numerous intriguing properties of numbers have led a great number of mathematicians and non-mathematicians to devote considerable energies to their study. The result has been the development of a beautiful and powerful theory, whose aim is to answer questions about the integers. Our goal is to study the elementary aspects of a wide array of techniques available to mathematicians. We begin with a description of some classical problems in number theory.
One of the oldest mathematical constructions is that of a
right triangle with integer sides. If a, b, and c are
the sides of the right triangle, then,
as it is well known,
(see Figure 1.1 for a proof). A triple of integers
(a,b,c) satisfying
is called a Pythagorean
triple. Here are a few examples of Pythagorean triples.
| a | 3 | 5 | 7 | 8 | 9 | 11 |
|---|---|---|---|---|---|---|
| b | 4 | 12 | 24 | 15 | 40 | 60 |
| c | 5 | 13 | 25 | 17 | 41 | 61 |
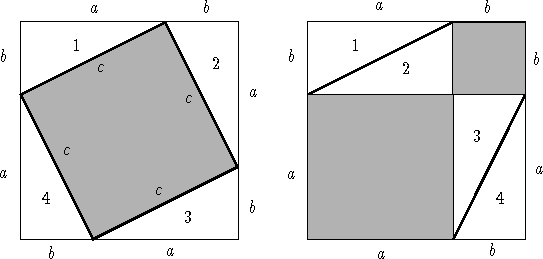
Figure 1.1: Proof of the Pythagorean Theorem
One of the earliest results in number theory (due to Greek
geometers) is a complete description of Pythagorean
triples. In this classification, one sees that the
hypotenuse is a multiple of a sum of two squares. For
example, 
, 
, etc. We can show that
3 and 7 are not values for the hypotenuse of a right triangle
because they are not a multiple of a sum of two integral squares.
One of the giants in the history of number theory is Pierre de Fermat. He determined which integers occur as the hypotenuse of a right triangle. Fermat showed that a prime number of the form 4k+1 occurs as the hypotenuse of a right triangle, but a prime of the form 4k+3 is never the hypotenuse of a right triangle. This result of Fermat follows from the study of representation of integers as a sum of two squares.
Fermat also studied the sums of four squares and conjectured that every natural number is the sum of four squares. For example,
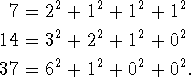
Fermat's conjecture was later proved by Joseph Louis Lagrange.
Mathematicians like Leonhard Euler, Adrien-Marie Legendre, and Carl
Friedrich Gauss studied
numbers of the form 
, 
, etc. This
study leads to the beautiful theory of quadratic forms
and the quadratic reciprocity law. An example of the
type of theorems that are proved in this theory is the
following: a prime number is represented in the form
if and only if it is of the form 20k+1 or
20k+9. For example, 
and 
.
Another source of speculation, since ancient times, has been about numbers arising from geometric figures. The triangular numbers are
The nth triangular number counts the number of dots in the triangle with n dots in each side. These are shown in Figure 1.2. Similarly, we define square and pentagonal numbers to correspond to the number of dots in the corresponding geometric shape. An interesting problem is to find numbers that are simultaneously square and triangular. For example, 1 and 36 are square and triangular. It is possible to find many more. The reader is invited to find a few more numbers that are square and triangular and to look for a relationship among them.
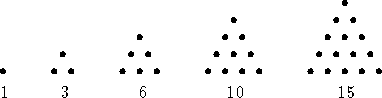
Figure 1.2: Triangular numbers
Fermat conjectured that every positive integer is a sum of at most three triangular numbers; every natural number is a sum of at most four square numbers; every natural number is a sum of at most five pentagonal numbers; and so on for hexagonal, heptagonal, and other polygonal numbers. For example, regarding the sum of triangular numbers, we have
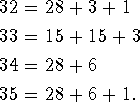
Gauss proved Fermat's conjecture for triangular numbers, as noted in his journal entry for July 10, 1796.
In studying the divisibility properties of integers, we soon find that there are some numbers that are not divisible by any other. These are the prime numbers; all other numbers can be factored into a product of prime numbers. The prime numbers are the basic building blocks of the integers; hence their study is of utmost importance in number theory.
The fundamental result about prime factorization is
also the source of one of the most difficult problems
in mathematics. How do we tell if a number is prime? If
it is not prime, how can we find its prime factors? It
is easy to see that 17 is prime, and with some
effort, we can see that 
is prime,
but it becomes very
difficult to decide if 
is prime.
Recent advances have made it possible for us
to check in a matter of seconds if a number with several
hundred digits is prime.
The problem of computing the prime factors of large composite numbers is considered intractable, and this difficulty is the source of numerous contemporary applications of number theory to cryptography. The science of cryptography deals with the transmission of secure information. The problem of integer factorization can be used in clever ways to construct secure cryptosystems. All of these are based on the proposition, which is yet to be proved, that integer factorization is a difficult problem.
The study of the distribution of prime numbers is another
important part of number theory. Euclid showed that there
are infinitely many primes, and Peter Gustav Lejeune Dirichlet showed that
there are infinitely many primes in every suitable
arithmetic progression. But for sequences which are not arithmetic
progressions, no
results are available. For example, no one knows if there
are infinitely many primes of the form 
or if there
are infinitely many primes of the form 
. Most
questions about the number of primes and their
distribution require the use of complex function theory.
Number theory is characterized by the ease with which one
can discover interesting facts, yet obtaining a rigorous proof of
these facts can frustrate the greatest mathematicians. Numerous
examples of facts discovered by computation, but whose
proofs are maddeningly difficult, can be found in the text.
Usually, a host of tools from different branches of
mathematics must be employed in their solution. Many
branches of mathematics have their origins in number
theory. For example, the attempts to prove that the equation
has no nontrivial solutions for 
(Fermat's Last Theorem) led to the development of ideal
theory of algebraic numbers. The problem spurred advances
in arithmetic and algebraic geometry. Fermat's Last
Theorem was finally settled by exploiting the connections
between elliptic curves and modular forms.
Even though Fermat's Last Theorem is without consequence,
attempts to solve it have led to the development of
important mathematics.
EXERCISES
1. Show that if there are integers r and s such that
then (a,b,c) forms a Pythagorean triple.
2. Find a right triangle with smallest leg of length 13.
3. Are there infinitely many right triangles in which the hypotenuse and a leg are consecutive integers?
4. Show that the nth triangular number is
.
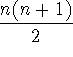5. The pentagonal numbers are shown in the Figure below. Determine a formula for the nth pentagonal number.
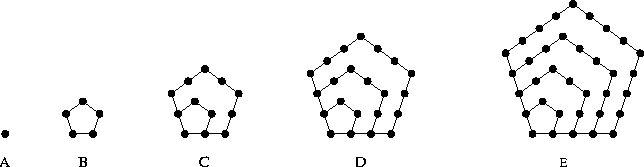
where A=1, B=5, C=12, D=22, E=35.
6. (Nicomanchus, 300 A.D.) Show that the sum of two consecutive triangular numbers is a square. Prove that the sum of the nth square and (n-1)st triangular numbers is the nth pentagonal number.
7. In how many ways can you express 84 as a sum of four squares?
8. Make a list of numbers that can be written as sums of three squares. Which numbers are not in your list? What can you say about the numbers that are not sums of three squares?
9. Write a computer program to verify Fermat's conjecture about the representation of natural numbers as sums of polygonal numbers.
10. Find all integer solutions to the equation
when 
.
11. Write a computer program to find integer solutions to the equation
. Are there infinitely many solutions?
In this chapter we introduce the basic notions of divisibility, primes, and unique factorization. The division algorithm and the Euclidean algorithm are the fundammental tools necessary for further study. The chapter includes a discussion of prime numbers, a proof of the Fundamental Theorem of Arithmetic, and properties of the greatest common divisor.
An application of the Euclidean algorithm is to the solution of linear diophantine problems. The projects at the end the chapter explore Pythagorean triples, perfect numbers, and Goldbach's conjecture.
The fundamental idea in the study of divisibility is the notion of congruences. Two integers a and b are said to be congruent modulo m if the difference a-b is a multiple of m. Congruences can be added and multiplied and this leads to a great simplification oof many computations. e.g. we can compute without much difficulty the last three digits of 97 raised to the 1997 power.
We study the basic arithmetic properties of congruences, solutions of linear congruences, of simultaneous congruences via the Chinese Remainder Theorem, and higher degree congruences.
Applications of this include properties of card shuffles. divisibility properties of binomial coefficients, and various criteria for divisibility.
This chapter studies the theorems of Fermat, Euler, and Lagrange. Fermat's theorem states that if p is prime, then n^p-n is a multiple of p for every n. This is the basic tool in the aritmetic of congruences. Euler generalized Fermat's theroem to composite moduli by introducing the phi-function. Lagrange's theorem gives an upper bound on the number of solutions to higher degree congruences moulo primes.