Previous Chapter
Next Chapter
Diophantine problems, named after Diophantus of Alexandria,
are concerned with the integral solution of polynomial
equations with integer coefficients. The following Diophantine
equations are discussed in the text.
- Pythagorean triples are integers
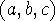such that
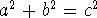. The triples are classified and the techniques
are generalized to equation of the form 
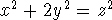and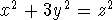 
. - Sums of two squares: Fermat's method of descent is
used
to show that every prime of the form 4k+1 is a sum of two
squares. From this, numbers expressible as sums of two squares
are characterized. The method of descent also applies to numerous other
problems such as sums of four squares and Markoff's equation.
- The equation
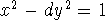(when d >0 is not a perfect
square) is solved using the continued fraction expansion of
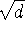. This equation was first studied by the Indian
mathematician
Brahmagupta
in the sixth century, and a complete solution was given by
Bhaskara,
in the eleventh century. - Fermat's famous conjecture (Fermat's Last Theorem)
states
that the equation
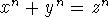has no integral solutions if
n>2 and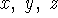 
are nonzero integers. This
was recently
established by Andrew
Wiles. We discuss the
case n=4, and a special case of the theorem that was proved
by Sophie
Germain.
The chapter has a large number of interesting exercises and
projects, including sums of four squares, the Markoff equation
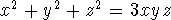, the solution of 
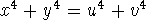, and
problems regarding polygonal numbers. Another project studies the following
problem of Fermat.
Fermat asked Mersenne for a right triangle with integer sides such that the
hypotenuse and the sum of the legs are squares.
The solution uses the classification of Pythagorean triples and the method of
descent.